牵手函数同构 拨开解题迷雾
——以指数、对数函数同构问题为例
2022-11-27福建省南平市高级中学353000
福建省南平市高级中学(353000)叶 燕
构造函数一向备受命题者的青睐,其中函数同构问题更成为近几年的高考命题热点,值得教师关注。2020年山东高考卷数学第21题把函数不等式恒成立与函数同构巧妙对接,成为函数同构的标志性试题,掀起的高潮延续至今。
函数同构一般是对题干中的方程、不等式做合理变形,使得方程或不等式两边呈现出相同的结构,然后根据相同结构构造函数f(x),并判断函数f(x)的单调性,最后利用函数f(x)的单调性求解。运用函数同构思想解题,能极大地优化解题过程,但并非所有的导数综合题都能运用函数同构解答。
那么,如何识别哪些题型适合运用函数同构来解题呢?又怎样才能更好地运用函数同构解题呢?归类解析就是一种好办法。为此,本文着重对指、对数函数的同构问题进行归类解析。
当题干或问题同时包含有ex和lnx的结构特征时,可考虑函数同构。对于指数、对数函数同构,多数可归为如下五种情形。
一、与函数f(x)= xex同构


二、与函数f(x)=ex + x同构
[例3]若不等式xm(ex+x) ≤emx+mxm(x−lnx)恒成立,则实数m的取值范围是___________。
解:因为x>0,所以原不等式等价于ex+x≤+mx−mlnx,即ex+x≤emx−mlnx+(mx−mlnx)恒成立。
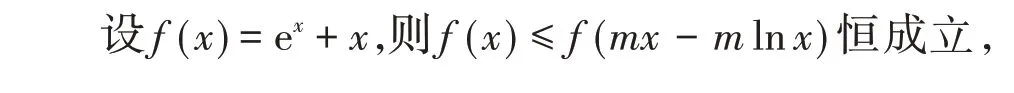

三、与函数f (x)=(x + c)ln x 同构,其中c为常数
[例5]已知函数f(x)=x(ex+1),g(x)=(x+1)lnx,则下列结论正确的是( )。

解:仅对D选项进行分析。
∵g(x2)=(x2+1)lnx2=(elnx2+1)lnx2=f(lnx2),
∴f(x1)=g(x2)=t(t>0),
∴f(x1)=f(lnx2)=t,可得x1>0,x2>1,


[例6]实数x1,x2满足x1ex1=e3,x2(lnx2−2)=e5则x1x2=__________。
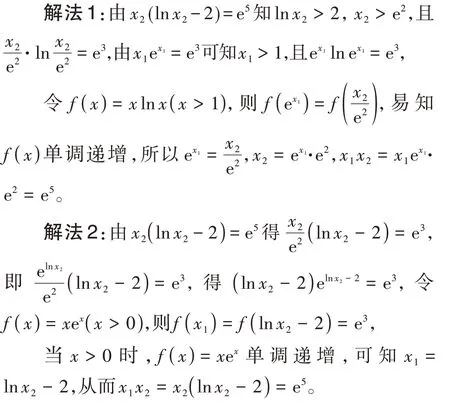
四、与函数f(x)= x+ln x同构

当x∈(−2,−1)时,h′(x) >0,h(x)单调递增,
当x∈(−1,+∞)时,h′(x) <0,h(x)单调递减,
∵lna>h(x)max=h(−1)=1,∴a>e。
解法2:因为a>0,所以由f(x)=−2 >0(x>−2),可得ex+lna+lna>ln(x+2)+2,两边加 上x,则ex+lna+(x+lna) >(x+2)+ln(x+2)=eln(x+2)+ln(x+2),
设g(x)=ex+x,则g(x+lna) >g[ln(x+2) ],∵g(x)=ex+x单调递增,∴x+lna>ln(x+2),即lna>ln(x+2) −x,
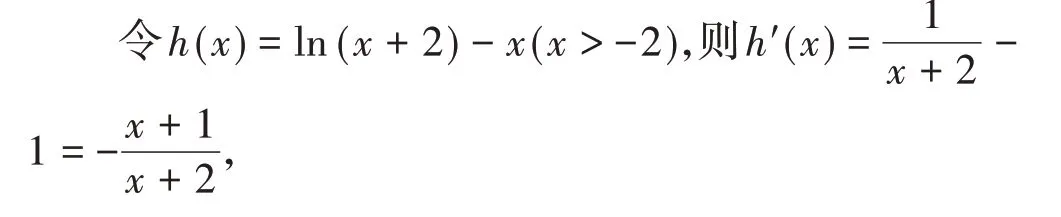
当x∈(−2,−1)时,h′(x) >0,h(x)单调递增,
当x∈(−1,+∞)时,h′(x) <0,h(x)单调递减,
∵lna>h(x)max=h(−1)=1,∴a>e。
五、与函数f(x)=同构

上述题目若按常规解法处理,将迷雾重重,相当棘手,而运用函数同构思想解决,则可拨云见日,柳暗花明。
在运用函数同构时,应当明确:
第一,先把相同变量放在同一边,再由内向外同构。对内同构,即通过合理变形实现左、右两边各自内部同构,这是同构的重点,也是难点。在例4 的分析中,方程左边两处经过变形匹配出的“2x+a”,即方程左边的内部同构,方程右边两处经过变形匹配出的“lnx”,即方程右边的内部同构。内部同构一旦完成,对外同构就自然生成。
第二,充分发挥恒等式“x=elnx和x=ln ex”在同构转化中的桥梁作用。同构的基本变形方法有两种:(1)变形为指数;(2)变形为对数。而具体的同构式,因变形的组合不同,可以有多种,如:
设a,b都为正数,若aea+1+b A.ab>e B.b>ea+1C.ab 解:把相同变量放在同一边,一边一个,得 第三,同构的相互转化。同构函数f(x)=xex和同构函数g(x)=xlnx可以相互转化;同构函数f(x)=ex+x和同构函数g(x)=x+lnx也可以相互转化。而例6和例7的两种解法,给了最直观的说明。 在上述题目中,指数、对数函数唱戏,幂函数搭台。下面分析一道幂函数、指数函数、对数函数、三角函数齐聚一堂的“恐怖题”,以再次感受运用同构思想解题之神奇魅力。

