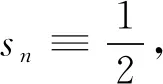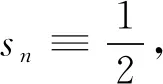广义黏性隐迭代序列的均衡问题和不动点问题

沈金良

(福州大学至诚学院，福建 福州 350002)

均衡理论和不动点理论是非线性分析的重要组成部分。很多学者对非扩张映射的不动点问题和均衡问题进行深入研究，建立更有效的迭代格式以逼近非扩张映射不动点集和均衡问题解集的公共元。近年来，许多学者不断从空间、迭代格式、证明方法以及算子等方面对已有的结论进行了推广,并取得了较好的研究结果，见文献[1-7]及其相关文献。

对于二元函数G:C×C→R，其均衡问题(以EP表示)可定义为：寻找x∈C，使得

G(x,y)≥0(∀y∈C)

(1)

将式(1)的解集记为EP(G)，即

EP(G)={x∈C:G(x,y)≥0,∀y∈C}

2015年，XU等[8]利用黏性逼近方法构造了非扩张映射隐中点迭代序列：

(2)

其中{αn}⊂(0,1)，f是压缩映射，T是非扩张映射, 并在Hilbert空间中得到了强收敛定理。

同一年， KE等[9]提出了广义黏性隐迭代序列：

xn+1=αnf(xn)+(1-αn)T[snxn+

(1-sn)xn+1],n≥0

(3)

其中{αn},{sn}⊂(0,1)，f是压缩映射，T是非扩张映射, 并在某些条件下得到了该序列的强收敛定理。

2018年，沈金良[10]研究了如下非扩张映射T的隐中点迭代序列：给定x1∈C，有

(4)

其中{αn}⊂(0,1)，{rn}⊂(0,∞)，并且在Hilbert空间中得到了该序列的弱收敛和强收敛定理。

2020年，沈金良等[11]研究了如下非扩张映射的隐中点黏性迭代序列：给定x1∈C，有

(5)

并且在Hilbert空间中证明了序列{xn}和{un}强收敛于F(T)∩EP(G)中的某一个点z，其中z=PF(T)∩EP(G)f(z)。

受到上述成果的启发，本文针对非扩张映射的不动点问题和均衡问题的公共解，利用黏性逼近技巧，在Hilbert空间中提出一种新的广义黏性隐迭代序列，并且在某些条件下证明了该迭代序列的强收敛性，所取得的成果推广了文献[10]和[11]的结论。

1 预备知识

文中始终假设H是实Hilbert空间，C是H的非空闭凸子集。序列{xn}弱收敛于x记为xn⇀x，以及{xn}强收敛于x记为xn→x。任取一点x∈H，则必可在C中找到唯一的最近距离点PC(x)，使得

‖x-PC(x)‖≤‖x-y‖,∀y∈C

称PC为H在C上的投影算子，则显然PC是非扩张映射，而且对于x∈H以及z∈C，有

z=PC(x)⟺〈x-z,z-y〉≥0,∀y∈C

为了求解均衡问题EP(G)，假设函数G满足以下4个条件：

(A1)G(x,x)=0,∀x∈C；

(A2)G是单调的，即G(x,y)+G(y,x)≤0,∀x,y∈C；

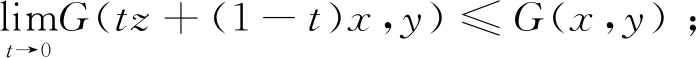
定义1设C是H的闭子集，T:C→C，f:C→C是两个映射。

(1)对于任意的x,y∈C，都有‖Tx-Ty‖≤‖x-y‖，则称T是非扩张映射。

(2)对于C中的序列{xn}，xn⇀x0∈H和Txn→0可以推导出Tx0=0，则映射T在0点是半闭的。

(3)对于任意的x,y∈C，存在常数α∈[0,1)，使得‖f(x)-f(y)‖≤α‖x-y‖, 则称f是压缩映射。

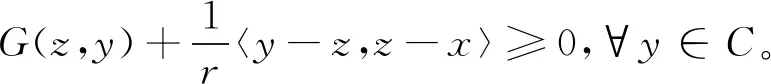
引理2[12]设映射G:C×C→R满足(A1)—(A4)。对r>0,x∈H，定义映射Sr:H→C为

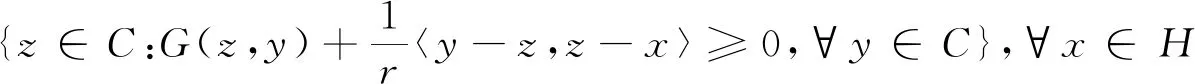
则有：

(1)Sr是单值的；

(2)Sr是稳定非扩张映射，即‖Srx-Sry‖2≤〈Srx-Sry,x-y〉,∀x,y∈H；

(3)G(Sr)=EP(G)；

(4)EP(G)是非空闭凸的。

引理3[13]设C是H的非空闭凸子集，T:C→C是非扩张映射。如果T有不动点，那么I-T在0点是半闭的(这里I是H中的恒等映射)，即如果C中的任意序列{xn}弱收敛于x∈C且有序列{(I-T)xn}强收敛到y，则有(I-T)x=y。

引理4[14]设{an},{bn}和{cn}是三个非负数列，{cn}⊂[0,1)并且满足以下条件：

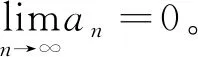
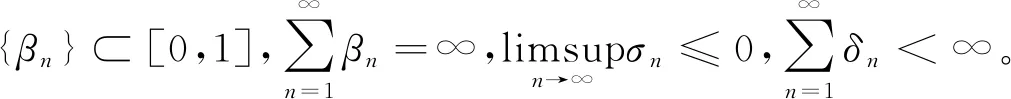
2 主要结论

定理1设C是H中的非空闭凸子集，G:C×C→R是二元函数，满足(A1)—(A4)。f:C→C是压缩映射，T:C→C是非扩张映射，Ω=F(T)∩EP(G)非空。任意给定x0∈C，{xn}和{un}的定义如下：

(6)

其中{αn},{sn}⊂(0,1)，{rn}⊂(0,∞)，并且满足以下条件：

本次研究所得数据的分析处理均采用SPSS21.0统计学软件进行,采用百分比(%)表示计数资料,行卡方值(X2)检验;采用均数±标准差(±s)表示计量资料,行t检验。若检验结果为P<0.05,则说明组间差异存在统计学意义。

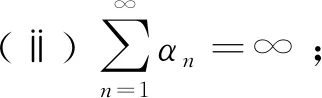
(ⅳ)0<ε≤sn<1(n≥1)；

则序列{xn}和{un}强收敛于z∈Ω，其中z=PΩf(z)。

证明下面分5步来证明定理1。

1)序列{xn}和{un}有界。

任取q∈Ω，由引理2可知un=Srnxn，因此

‖un-q‖=‖Srnxn-Srnq‖≤‖xn-q‖,∀n≥1

(7)

为了书写方便，令zn=snun+(1-sn)xn+1，则有xn+1=αnf(xn)+(1-αn)Tzn。

‖xn+1-q‖=‖αnf(xn)+(1-αn)Tzn-q‖

≤αn‖f(xn)-q‖+(1-αn)‖Tzn-q‖

≤αn‖f(xn)-f(q)‖+αn‖f(q)-q‖+(1-αn)‖zn-q‖

≤αnα‖xn-q‖+αn‖f(q)-q‖+

(1-αn)sn‖un-q‖+

(1-αn)(1-sn)‖xn+1-q‖

(8)

对式(8)进行移项，结合式(7)整理得

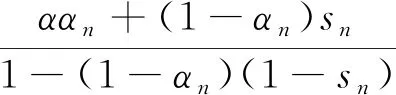
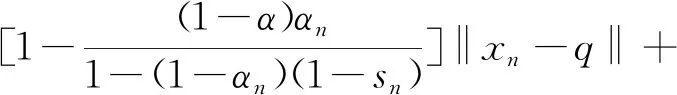
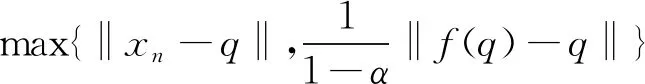
由递推公式可知

(9)

所以{xn}是有界序列，同时{un},{Txn},{Tun},{Tzn}也都是有界的。

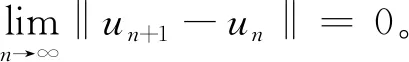
因为xn+1=αnf(xn)+(1-αn)Tzn，所以

‖xn+1-xn‖=‖αnf(xn)+(1-αn)Tzn-αn-1f(xn-1)-(1-αn-1)Tzn-1‖

=‖αnf(xn)-αnf(xn-1)+αnf(xn-1)-

αn-1f(xn-1)+(1-αn)Tzn‖-

(1-αn)Tzn-1+(1-αn)Tzn-1-

(1-αn-1)Tzn-1‖

≤αn‖f(xn)-f(xn-1)‖+|αn-αn-1|×

‖f(xn-1)-Tzn-1‖+(1-αn)‖Tzn-Tzn-1‖

≤αnα‖xn-xn-1‖+|αn-αn-1|K+(1-αn)‖zn-zn-1‖

=αnα‖xn-xn-1‖+|αn-αn-1|K+(1-αn)‖snun+(1-sn)xn+1-sn-1un-1-(1-sn-1)xn‖

=αnα‖xn-xn-1‖+|αn-αn-1|K+(1-αn)‖sn(un-un-1)+

(1-sn)(xn+1-xn)+

(sn-sn-1)(un-1-xn)‖

≤αnα‖xn-xn-1‖+|αn-αn-1|K+(1-αn)sn‖un-un-1‖+

(1-αn)(1-sn)‖xn+1-xn‖+

(1-αn)|sn-sn-1|‖un-1-xn‖

(10)

其中，K=sup{‖f(xn)-Tzn‖:n∈N}。

由式(6)可得

(11)

(12)

在式(11)中取y=un，则有

(13)

在式(12)中取y=un+1，则有

(14)

把式(13)和式(14)相加，再根据(A2)进行整理可得

所以

‖un+1-un‖2≤〈un+1-un,xn+1-xn+

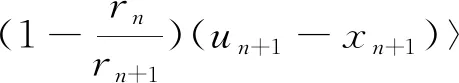
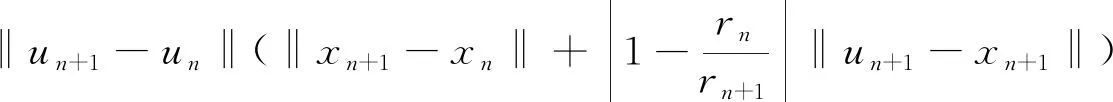
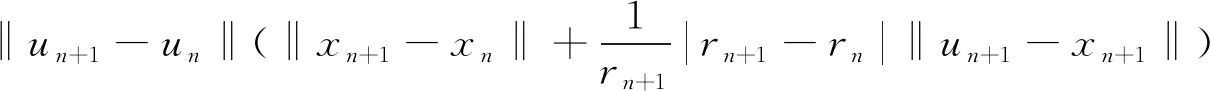
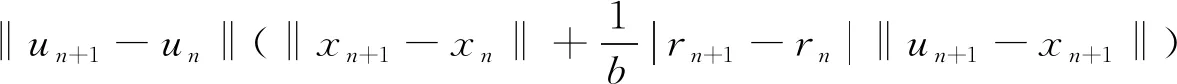
(15)

取L=sup{‖un-xn‖:n∈N}, 由式(15)得

(16)

因为{xn}和{un}都是有界序列，所以{‖un-1-xn‖}也是有界的，因此存在实数M>0，使得

‖un-1-xn‖≤M,∀n≥1

(17)

由式(10)、(16)和(17)可得

‖xn+1-xn‖≤αnα‖xn-xn-1‖+|αn-αn-1|K+

(1-αn)sn(‖xn-xn-1‖+

(1-sn)‖xn+1-xn‖+

(1-αn)|sn-sn-1|M

对上式进行移项整理得

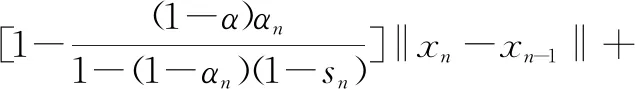
(18)

因为0<ε≤sn<1，所以必有0<ε≤sn<1-(1-αn)(1-sn)<1。由式(18)可得

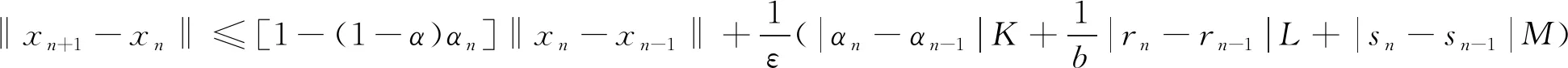
(19)

再由式(16)和‖rn+1-rn‖→0(n→∞)可得

(20)

任取q∈Ω，由un=Srnxn可知

‖un-q‖2=‖Srnxn-Srnq‖2

=〈Srnxn-Srnq,un-q〉

≤〈un-q,xn-q〉

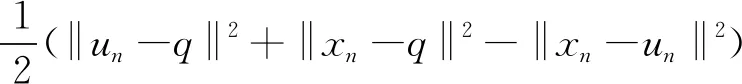
即有

‖un-q‖2≤‖xn-q‖2-‖xn-un‖2

(21)

由式(21)有

‖xn+1-q‖2=‖αn[f(xn)-q]+(1-αn)[Tzn-q]‖2

≤αn‖f(xn)-q‖2+(1-αn)‖Tzn-q‖2

≤αn‖f(xn)-q‖2+(1-αn)sn‖un-

q‖2+(1-αn)(1-sn)‖xn+1-q‖2

≤αn‖f(xn)-q‖2+(1-αn)sn‖xn-

q‖2-(1-αn)sn‖xn-un‖2+

(1-αn)(1-sn)‖xn+1-q‖2

上式移项整理得

(1-αn)sn‖xn-un‖2

≤αn‖f(xn)-q‖2+(1-αn)sn‖xn-q‖2+

[(1-αn)(1-sn)-1]‖xn+1-q‖2

≤αn‖f(xn)-q‖2+(1-αn)sn(‖xn-q‖2-

‖xn+1-q‖2)-αn‖xn+1-q‖2

≤αn‖f(xn)-q‖2+(1-αn)sn‖xn+1-xn‖×

(‖xn-q‖+‖xn+1-q‖)-αn‖xn+1-q‖2

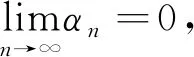
(22)

由条件(ⅰ)(ⅴ)，式(19)(20)可得

‖xn-Tzn‖≤‖xn-Tzn-1‖+‖Tzn-1-Tzn‖

≤αn-1‖f(xn-1)-Tzn-1‖+‖zn-1-zn‖

≤αn-1‖f(xn-1)-Tzn-1‖+

(1-sn)‖xn+1-xn‖+

sn‖un-un-1‖+|sn-sn-1|×

‖un-1-xn‖→0(n→∞)

(23)

由式(19)、(22)和式(23)得

‖un-Tun‖≤‖un-xn‖+‖xn-Tzn‖+‖Tzn-Tun‖

≤‖un-xn‖+‖xn-Tzn‖+

(1-sn)‖xn+1-xn‖+(1-sn)‖xn-un‖

=(2-sn)‖un-xn‖+‖xn-Tzn‖+

(24)

再由式(22)和式(24)得

‖xn-Txn‖≤‖xn-un‖+‖un-Tun‖+‖Tun-Txn‖

≤2‖xn-un‖+‖un-Tun‖→0(n→∞)

(25)

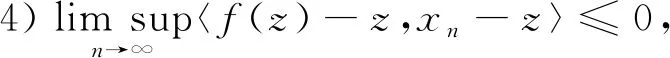
由式(22)，可取{un}的一个子列{uni}，使得

因为{uni}有界，所以存在{uni}的一个子列{unij}弱收敛于v。不失一般性，直接假设univ。由‖un-Tun‖→0(n→∞)，可知Tuniv。下面证明v∈Ω。因为

下面证明v∈F(T)。T是非扩张映射，由引理3可知I-T在0点是半闭的。由前面的证明可知‖un-Tun‖→0和uni⇀v，所以v∈F(T)。由此证得v∈Ω。因z=PΩf(z)，故可得

=〈f(z)-z,v-z〉≤0

(26)

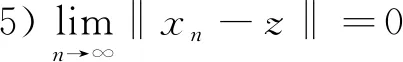
由范数和內积的性质可知

‖xn+1-z‖2≤(1-αn)2‖Tzn-z‖2+

2αn〈f(xn)-z,xn+1-z〉

≤(1-αn)2‖snun+(1-sn)xn+1-z‖2+

2αn〈f(xn)-f(z),xn+1-z〉+

2αn〈f(z)-z,xn+1-z〉

≤(1-αn)2sn‖un-z‖2+

(1-αn)2(1-sn)‖xn+1-z‖2+

2ααn‖xn-z‖‖xn+1-z‖+

2αn〈f(z)-z,xn+1-z〉

≤(1-αn)2sn‖xn-z‖2+

(1-αn)2(1-sn)‖xn+1-z‖2+

ααn(‖xn-z‖2+‖xn+1-z‖2)+

2αn〈f(z)-z,xn+1-z〉

因此

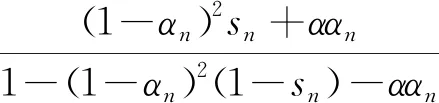
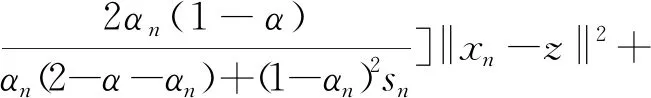
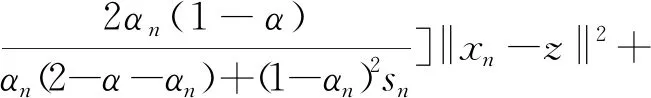
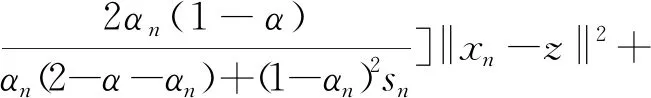
=(1-βn)‖xn-z‖2+βnσn

其中

I=sup{‖xn-z‖2:n∈N}

(27)

(28)

由上述证明过程可知，序列{xn}和{un}强收敛于z∈Ω，同时z也是变分不等式〈(I-f)y,x-y〉≥0,x∈Ω的唯一解，即z=PΩf(z)。