地铁车站结构设计细节优化研究

刘 晨 李 标

地铁作为城市轨道交通的重要组成内容，具有乘客密集、环境封闭、线路位于地表以下的特征，为保障乘客的出行安全，必须做好地铁结构设计。结合实际情况，传统地铁车站设计以结构自重、水土压力以及地铁超载等静载荷为主要设计指标，但此设计方式中忽略了地震因素对车站结构的影响，以此为施工依据可能会存在安全隐患。

因此，本文在地铁车站设计分析中引入了结构抗震环节，并且通过有限元仿真分析方法确认不同地铁车站结构设计细节部分需要重点关注的内容，保障设计的合理性，降低了地铁车站的安全风险[1]。

1 工程概况

某地铁车站全长为273 m，地下2层采用狭长箱型结构，标准段外包宽度为20 m。车站采用浅埋暗挖法施工，施工区域内部设置盾构井，主体结构中标准段顶板、底板、中板厚度分别为800 mm、900 mm、400 mm，均采用C35 混凝土；端头井顶板、底板、中板以及侧墙的厚度分别为800 mm、1 000 mm、400 mm、600 mm，均采用C35 混凝土；地下连续墙厚度为800 mm，采用C35 混凝土；单柱尺寸为700 mm×1 200 mm、双柱尺寸为600 mm×1 100 mm，均采用C40 混凝土。工程地质区域属于第四纪冲洪积平原区，区域内土层主要由人工填土层、第四纪沉积粉质土、黏性土、砂土以及碎石土组成，地下水位在地面以下20 m。

2 地铁车站结构仿真模型构建

根据某地铁车站的实际情况，确定采用SAP2000 有限元分析软件进行模型构建，模型网格单元尺寸设置为0.5 m。模型中结构部分采用框架单元进行仿真模拟，底板土压力采用只受压弹簧模拟。

将某地铁车站标准段横断面具体参数输入至模型后，运行模型进行仿真计算分析。

3 地铁车站结构的有限元仿真分析

3.1 标准段横断面分析

对某地铁车站结构关键部位弯矩和剪力包络图数据统计分析后，确认某地铁车站标准段弯矩及剪力如表1 和表2所示。

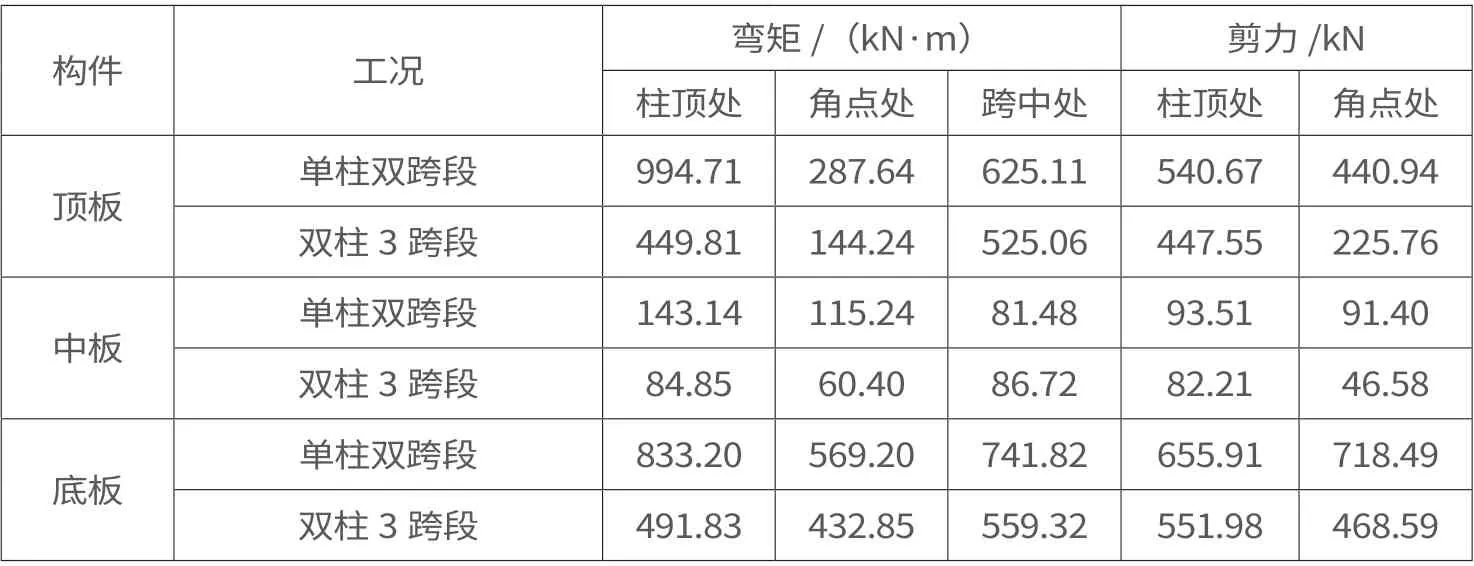
表1 某地铁车站标准段横断面顶板、中板、底板弯矩及剪力统计表

表2 某地铁车站标准段横断面侧墙弯矩及剪力统计表

3.2 结构静力学分析

将以上的参数及某地铁车站实际数据输入有限元仿真软件中，为模型配置基本参数值后实施结构变形以及结构内力仿真分析。据仿真分析结果可知，某地铁车站单柱双跨段结构最大弯矩为948.512 6 kN·m，位于单柱双跨段底板箱型结构角点区域；最大剪力698.642 1 kN，位于单柱双跨段底板箱型结构角点区域。双柱3 跨结构仿真分析过程与单柱双跨段结构仿真分析过程基本一致。通过仿真分析可知，双柱3 跨段结构的最大弯矩为591.246 kN·m，位于双柱3 跨段底板箱型结构角点区域和侧向底板区域；最大剪力为445.621 6 kN，位于双柱3 跨段底板箱型结构角点区域。

3.3 地震工况分析

在静力学仿真分析的基础上引入地震作用，获取地震工况下某地铁车站结构的性能数据。通过仿真分析结果可知，某地铁车站单柱双跨段结构的最大弯矩为958.661 3 kN·m，位于单柱双跨段底板箱型结构角点区域和侧向底板区域；最大剪力为731.715 5 kN，位于单柱双跨段侧墙底板区域。

双柱3 跨段结构的最大弯矩为978.565 1 kN·m，位于双柱3 跨段底板箱型结构角点区域和侧向底板区域；最大剪力为745.217 kN，位于双柱3 跨段侧墙底板区域。

4 地铁车站结构性能影响因素及设计细节优化方向

4.1 单柱双跨段

对某地铁车站静力学分析和地震工况分析的结果进行归纳，从而形成表3和表4 中的仿真分析结果。

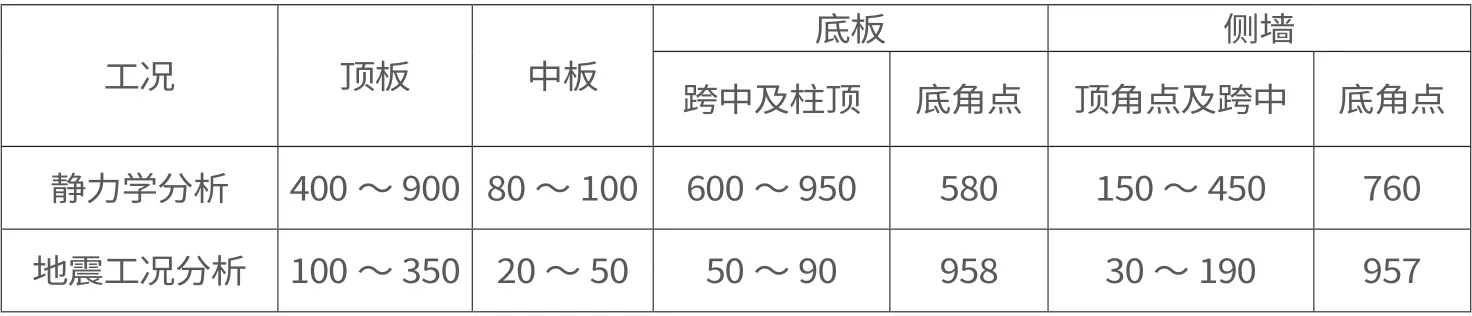
表3 静力学分析与地震工况分析下弯矩对比（单位：kN·m）

表4 静力学分析与地震工况分析下剪力对比（单位：kN）

由表3 和表4 可知，对于地铁车站结构的顶板，静力学分析和地震工况分析中顶板柱顶、跨中及角点等区域弯矩值为400 ～900 kN·m 和100 ～350 kN·m；静力学和地震工况分析中柱顶和角点区域的剪力400 ～600 kN 和50 ～300 kN。为保障地铁车站顶板的综合安全系数，顶板结构设计中应取较大值，即顶板弯矩及剪力计算应按照静力学分析过程进行计算和控制[2]。

对于地铁车站结构的中板，静力学分析和地震工况分析中，其柱顶、跨中以及角点等区域的弯矩值均分别处于80 ～100 kN·m 和20 ～50 kN·m；静力学分析和地震工况分析中板中柱顶和角点区域的剪应力分别处于80 ～90 kN和10 ～30 kN。为保障地铁车站中板的综合安全系数，中板弯矩及剪力计算应按照静力学分析过程进行计算和控制。

对于地铁车站结构的底板，静力学分析和地震工况分析中，底板柱顶和跨中以及角点等区域弯的矩值分别处于600 ～950 kN·m 和580 kN·m、50 ～90 kN·m 和958 kN·m；静力学分析和地震工况分析中底板柱顶和角点区域的剪应力分别处于650 ～700 kN 和50 ～450 kN。为保障地铁车站底板的综合安全系数，底板弯矩及剪力计算应按照静力学分析过程进行计算和控制。

对于地铁车站结构的侧墙，静力学分析和地震工况分析中，侧墙顶点及跨中、底角点弯矩分别处于150 ～450 kN·m和760 kN·m、30 ～190 kN·m 和957 kN·m；静力学分析和地震工况分析中侧墙顶板、中板及底板处的剪应力分 别 为190 kN 和250 kN、490 kN 和130 kN、480 kN 和730 kN。为保障某地铁车站侧墙的安全系数，综合分析后确认侧墙顶角点及跨中弯矩应采用静力学分析，底角点弯矩应采用地震工况分析；中板处剪应力应采用静力学分析，顶板和底板处剪力应采用地震工况分析[3]。

4.2 双柱3 跨段

对某地铁车站静力学分析和地震工况分析的结果进行归纳，形成表5 和表6中的仿真分析结果。

表5 静力学分析与地震工况分析下弯矩对比（单位：kN·m）

表6 静力学分析与地震工况分析下剪力对比（单位：kN）

对于地铁车站结构的顶板，相较于静力学分析，地震工况分析下角点和边跨跨中弯矩更大，而柱顶及中跨跨中弯矩较小；同时，相较于静力学分析，地震工况分析下顶板柱顶及角点剪力较小。为保障地铁车站顶板的综合安全系数，顶板结构设计中应取较大值。因此，地铁车站结构顶板柱顶、中跨跨中处弯矩计算应优先选择静力学控制；角点、边跨跨中弯矩应优先选用地震工况控制；顶板剪力计算应优先采用静力学控制。

对于地铁车站结构的中板，相较于静力学分析，地震工况分析下柱顶及中跨跨中、边跨跨中及角点弯矩均较小；同时，相较于静力学分析，地震工况分析下中板柱顶及角点剪力相对较小。因此，地铁车站结构中板弯矩及剪力计算均应优先采用静力学控制[4]。

对于地铁车站结构的底板，相较于静力学分析，地震工况分析下柱顶及中跨跨中弯矩相对较小，而边跨跨中及角点弯矩相对较大；相较于静力学分析，地震工况分析下柱顶和角点处剪力均相对较大。因此，地铁车站结构底板柱顶及中跨跨中弯矩计算应优先选用静力学控制，而跨中及角点弯矩计算应优先选用地震工况控制；底板剪力应优先选用地震工况控制[5]。对于地铁车站结构的侧墙，相较于静力学分析，地震工况分析下顶板处及地下1 层跨中和底板处弯矩相对较大，而中板处及地下2 层跨中弯矩相对较小；同时，相较于静力学分析，地震工况分析下侧墙顶板处和底板处剪力相对较大，而中板处剪力相对较小。因此，地铁车站结构侧墙弯矩计算中顶板处及地下1 层跨中和底板处弯矩计算应优先选用地震工况控制，中板处及地下2层跨中弯矩计算应优先选用静力学控制；侧墙剪力计算中顶板处和底板处剪力计算应优先选用地震工况控制，中板处剪力计算应优先选用静力学控制[6]。

5 结语

本文以某地铁车站为研究对象，结合地铁车站的实际数据，通过仿真分析方法获取某地铁车站结构设计细节优化方向及控制要点。根据文中分析结果可知，某地铁车站单柱双跨结构断面区域内的底板角点和侧墙底板角点及跨中抗弯性能、侧墙顶、底角点抗剪性能均需要根据地震工况控制进行相应加强；双柱3 跨结构断面中顶板、中板以及底板角点和跨中抗弯性能、地下1 层侧墙跨中和地下2 层侧墙底角点抗弯性能、侧墙顶角点和底角点抗剪性能均需要根据地震工况控制实施相应加强。