机器人关节非线性摩擦模型关键参数反求1)
2022-12-18段书用段浩东李昌洛欧阳衡李雨乐刘桂荣
段书用 * 段浩东 * 韩 旭 *,2) 李昌洛 * 欧阳衡 * 李雨乐 * 刘桂荣 **
* (河北工业大学省部共建电工装备可靠性与智能化国家重点实验室,天津 300131)
† (河北工业大学机械工程学院,天津 300131)
** (辛辛那提大学航空工程和机械工程系,美国辛辛那提 45221)
引言
随着机器人技术的不断发展,机器人的应用范围越来越广,在航天航空[1]、3C 制造[2]、外科手术[3]等高精密加工制造领域应用越来越多,对于精度和可靠性要求也越来越高.但是机器人在长期运行过程中,由于机件磨损、润滑油脂失效,自然腐蚀和其他原因,轨迹精度难免出现细微偏差,可靠性降低,甚至还会成为影响生产安全和产品质量的一大隐患,给生产和运行带来麻烦.因此必须定期对机器人进行维护来保证精度,必要时需要进行一些繁琐困难的辨识工作和标定工作来提升机器人轨迹精度,造成维护成本过高.而由机器人关节内部减速器磨损和润滑油脂失效导致的机器人关节摩擦参数变化是导致机器人轨迹精度降低的一个重要的影响因素[4-5].因此,有必要在摩擦参数和实际摩擦情况不匹配时,快速反求出变化后摩擦参数,进行摩擦补偿来提高轨迹精度,以满足实际工程需要,为机器人后期维护提供更加便捷的方式.
摩擦是一个非常普遍的现象,但是又十分复杂.众多研究学者对摩擦现象进行了相关分析,建立了多种摩擦模型来描述.摩擦模型主要分为静摩擦模型(如库仑模型、黏性模型、Stribeck 摩擦模型)和动摩擦模型(如Dahl 模型和LuGre 模型)[6].动摩擦模型是在静摩擦模型的基础上使用附加的状态变量来描述摩擦的动态行为[7].虽然动摩擦模型在描述关节摩擦特性方面比静摩擦模型更接近实际情况,但在复杂工况下很难保证摩擦力矩的获取精度,尤其动态参数的确定较为困难,而且鲁棒性欠佳.因此,有关机器人关节摩擦模型的研究多基于静摩擦模型,如采用静摩擦模型中的库仑模型描述机器人关节的干摩擦系统[8];采用库仑模型和黏性模型的组合描述机器人关节高速状态下的摩擦分布[9].虽然库仑模型和黏性模型在一定程度上反映了机器人关节干摩擦及高速状态下的摩擦分布情况,但库仑模型、黏性模型及其组合模型均未考虑关节低速运动时摩擦的非线性特点和换向过程中关节摩擦力矩不连续问题[10].基于此,陶岳等[11]通过在库仑+黏性摩擦模型中引入Sigmod 函数,尽管未考虑关节低速运动时摩擦的非线性特点,但克服了机器人关节在换向中摩擦力矩不连续问题,有效降低了关节换向过程中的轨迹跟踪误差.Bo 等[12]充分考虑了关节低速运动时摩擦的非线性特点,建立了Stribeck 摩擦模型.相关研究发现,在一定条件下Stribeck 摩擦模型对关节低速时摩擦模型的非线性描述精度高达90%[13-14],和动摩擦模型相比,结构简单,适应性较广,但Stribeck 摩擦模型未考虑换向过程中关节摩擦力矩不连续问题.张铁等[15]通过引入线性函数方法改进了Stribeck 摩擦模型,从而解决了传统Stribeck摩擦模型未考虑换向过程中关节摩擦力矩不连续的问题,在一定程度上减小了关节输出力矩的误差.
虽然现有摩擦模型在一定程度上定性地描述了关节角速度与摩擦力矩间的关系,但关节摩擦计算的准确性决定了机器人各关节摩擦力矩与驱动力矩的匹配性.当机器人各关节摩擦力矩与驱动力矩不匹配将导致机器人末端运动时产生爬行、抖动等现象,严重影响机器人的轨迹精度与平稳性[16].因此,相关研究者对摩擦模型参数的辨识展开了细致深入的研究.目前,基于计算反求技术的参数辨识方法主要有最小二乘法[17-19]、群体智能算法[20-22]和神经网络[23-26]等.陈光胜等[17]基于泰勒高次展开法将Stribeck 摩擦模型线性化后采用最小二乘拟合的方法对摩擦模型参数进行了辨识;张铁等[15]用混合遗传算法对改进的Stribeck 摩擦模型的参数进行了辨识;Tu 等[23]在考虑负载的情况下通过神经网络对摩擦力矩进行了反求;刘海荣等[24]采用模糊神经网络对伺服系统的LuGre 摩擦模型参数进行了辨识.
然而,机器人关节摩擦具有强非线性及时变性,不仅关节摩擦力矩随机器人位姿的变化而变化,而且受诸多不确定性因素影响,如润滑剂黏度、工作温度[27-28]、外力/扭矩水平、接触面粗糙度[29]、材料特性和表面拓扑结构等[30],导致关节摩擦模型难以准确描述.因此一些学者对摩擦模型的不确定性建模进行了分析,Lahriri 等[31]通过实验测得了转子和定子接触时干摩擦系数的上下界.Petrov[32]针对摩擦与间隙接触界面参数的不确定性,提出了一种计算非线性状态强迫响应水平不确定性的方法.Bitencourt 等[33]基于实验观察,提出了一个扩展的摩擦模型,即使在负载和温度不确定性下,也可以实现准确的磨损估计.吴晓敏等[34]在考虑温度变化的情况下,对机器人摩擦进行了分析.Huang 等[35]提出了一种扩展的动态参数集(EDS),并通过仿真和实验证明,基于EDS 模型可以大大补偿摩擦模型的不确定性.鉴于机器人关节摩擦受众多不确定性因素影响,很难获取普适性强的精确摩擦模型对其进行描述.因此,相关研究者采用跳过摩擦建模的方法,从控制的角度出发,把摩擦力矩当作外部干扰项或不确定项,通过反馈控制消除其对轨迹精度的影响,提升关节系统抗干扰能力.李坤龙等[36]用干扰观测器估计摩擦力的大小并对其进行了补偿,提高系统的运行稳定性.Yao 等[37]在考虑了参数不确定性的情况下,提出了一种自适应鲁棒控制方法,提高机器人系统的跟踪精度.但通过反馈控制方法补偿摩擦力影响往往需要很大的反馈增益,增加硬件成本,容易激发极限环震荡、增大传感器噪声等问题,而且对关节缓慢运动和转向的跟踪效果较差.
综上所述,通过反求摩擦参数,建立摩擦模型进行前馈补偿,可以提前预测摩擦力矩并消除摩擦力矩对机器人的影响,提高机器人的运动精度.因此,本文提出了一种通过神经网络反求摩擦参数的方法.首先,通过恒速跟踪实验测得在不同速度下的摩擦力矩,建立非线性摩擦模型.其次,通过建立机器人模型的方式建立摩擦参数和关节驱动力矩之间的关系,在此基础上对摩擦模型开展全局灵敏度分析,找到影响其性能的关键参数.然后,通过拉丁超立方抽样方法在采样空间内抽样,建立数据集.最后,建立神经网络,进行训练并对摩擦参数反求,并用反求的摩擦参数进行摩擦力矩补偿,验证反求参数的精确性和该方法对于机器人维护的便捷性.
1 关节非线性摩擦模型建立
本节基于恒速跟踪实验得到关节速度与其摩擦力矩关系的一般表达式[38].首先对恒速跟踪实验的原理和实施步骤进行详细描述,再对所测得的数据经过卡尔曼滤波进行处理,消去环境噪声,最后经过数据拟合,建立关节非线性摩擦模型.
1.1 恒速跟踪实验
机器人的电机、减速器与连杆间的力传递关系如图1 所示,由电流Ic驱动关节内的电机产生驱动力矩 τm,经关节内的减速器将驱动力矩 τm放大后传递给机器人相应的连杆,从而使得机器人运动.由此可得电机的驱动力矩
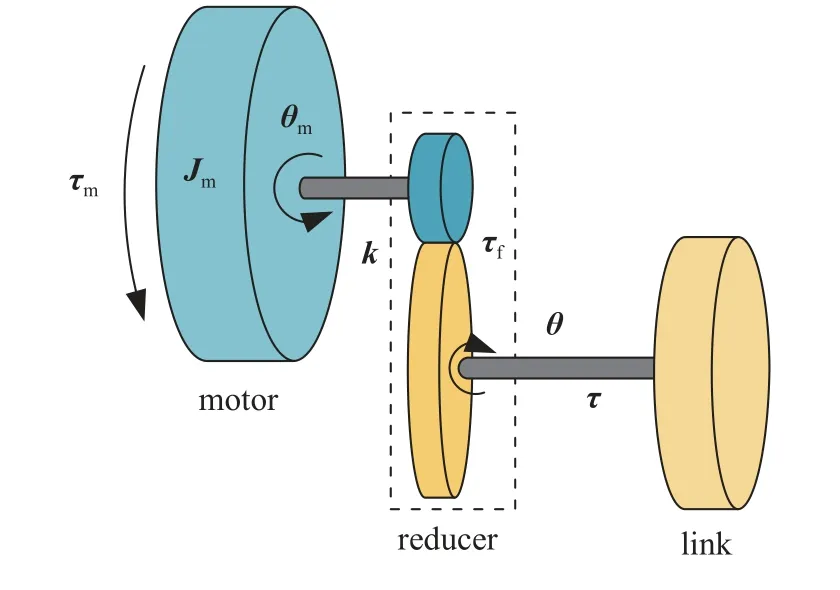
图1 关节结构Fig.1 The structure of joint

其中,Kτ∈R6×6为电机转矩常数矩阵,对角线上为各个关节电机转矩常数,其余位置为0;Ic∈R6×1代表驱动电流矩阵.Kτ中元素的数据由表1 所示.
由电机、减速器与连杆间的力传递关系可得
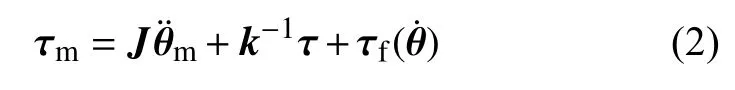
其中,J∈R6×6为折算到电机轴上的总转动惯量矩阵,对角线上为折算到各个关节电机轴上的转动惯量,其余元素为0;∈R6×1表示电机轴角加速度矩阵;τ ∈R6×1为连杆的驱动转矩矩阵;k∈R6×6是减速器的减速比矩阵,对角线上为各个关节减速器减速比,其余元素为0;τf∈R6×1为电机端摩擦力矩矩阵.k中元素的数据和电机转子的转动惯量Jm 由表1所示.

表1 关节电机参数Table 1 Motor parameters of joint
将式(1)和式(2)联立可得关节摩擦力矩表达式
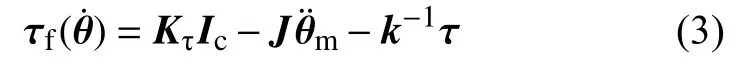
由于机器人连杆的驱动转矩为

由传动比关系可得

将式(4)和式(5)代入式(3)可得

由于Kτ已知,电流Ic可以测得,因此只需消除惯性力、科氏力和连杆重力影响,便可通过测量电机驱动电流计算得到电机端摩擦力矩

因此,设计机器人的恒速跟踪实验核心思想如下.

(3)消除连杆重力影响即G(θ)=0 : 设置旋转关节i平行于重力方向.
恒速实验具体实施如下:
为了测量不同关节的角速度与摩擦力的关系,保持关节i的轴线平行于重力方向,并锁定其他关节,驱动被测关节匀速运动.如图2 所示,以角速度将关节i从位置2 顺时针(CW)转动到位置1,再以相同的角速度从位置1 逆时针(CCW)旋转到位置2,测量关节恒速转动中的电流信号.设定关节角速度采样空间0.5 °/s~ 15 °/s,由于低速区摩擦力矩呈非线性分布,高速区摩擦力矩呈线性分布,所以在低速区0.5 °/s~ 5 °/s 以速度0.25 °/s 为间隔进行采样,高速区5 °/s~ 15 °/s 以2.5 °/s 为间隔进行采样,共采得23 个速度样本,每个速度样本重复做5 次采集实验.通过式(7)将得到的电流信号转换为摩擦力矩,由于电机控制器上数字电路的高速翻转和芯片控制部分的快速切换,测量的电流信号会产生高频噪声,所以通过电流得到的摩擦力矩也会有同样的噪声特征.因此,需将5 次重复实验计算得到的摩擦力矩数据滤波后统计平均.

图2 消除载荷的恒速跟踪实验布置图Fig.2 Constant velocity tracking experiment layout with load elimination
以关节3 的摩擦力矩数据为例,对其滤波过程进行详细说明.如图3 所示,关节3 以0.5 °/s 速度逆时针运动计算其力矩采样点raw data (CCW)在0.08~0.18 N·m 之间分布,顺时针运动时的力矩采样点raw data (CW)在−0.18~ −0.08 N·m 之间分布.对于高频噪声的滤波既要达到降噪的要求,又要确保滤波后的数据不失真.因为噪声符合高斯分布,而卡尔曼滤波是线性高斯系统的最优无偏估计,使测量数据方差最小,可以很好消除噪声.

图3 关节3 摩擦力矩滤波Fig.3 Friction torque filtering of joint 3
在恒速跟踪实验中,这个系统是一个静态的一维系统,可以用离散型状态空间方程表达这个系统为

其中,xk表示k时刻驱动力矩的状态值,A为系统系数,B为控制系数,u k−1为k−1 时刻的输入值,w k−1为k−1时刻的过程噪声

其中,zk为k时刻的驱动力矩的观测值,H为观测系数,vk为k时刻的测量噪声.
卡尔曼滤波主要分为以下预测和校正两个阶段
(1)预测阶段


(2)校正阶段
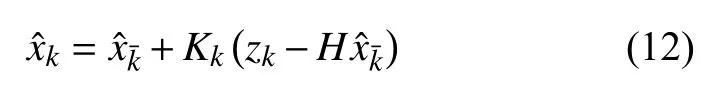
其中,K k表示k时刻卡尔曼增益
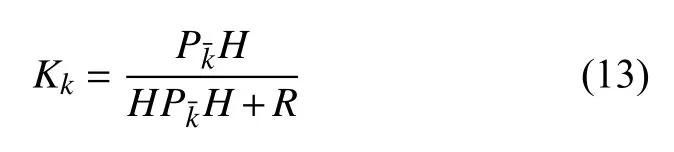
其中,R表示测量噪声v的方差

因为实验是在单一关节做恒速运动时测量的力矩值,所以此时这个系统可以看做是一个静态系统,因此并没有输入,所以u k−1=0,B=0 ,所以系统系数A=1.zk是观测到的力矩值,是真实值和测量噪声的叠加,所以观测系数H=1.可以通过设置Q和R的值来调整滤波效果,因为单关节保持恒速运动,并且实验过程中并没有引入其他额外干扰,所以此时过程噪声w非常小,因此将Q设置为1 × 10−6,根据经验将R设置为0.01.由图3 可知,滤波后力矩值的离散程度远小于原始数据.由表2 可以看出,过滤后的数据方差比原始数据方差降低了2 个数量级.因此,采用滤波后的数据和真实情况更为接近.

表2 力矩数据方差Table 2 Variance of torque data
1.2 非线性摩擦模型的建立
通过以0.5 °/s~ 15 °/s 速度驱动3 个关节分别恒速运动,并对采集的力矩采样点进行滤波,得到了沿速度梯度分布的摩擦力矩值.取同一速度下摩擦力矩均值,得到关节3 摩擦力矩相对于速度 θi的分布,如图4 所示.采用4 参数非线性摩擦模型式(15)可以很好地拟合分布关系,拟合的摩擦参数如表3 所示.

表3 非线性摩擦模型参数拟合值Table 3 Parameters of nonlinear friction model of fitting

图4 关节3 摩擦模型拟合Fig.4 Fitting of friction model of joint 3

式中,fci代表第i个关节库仑摩擦系数;fsi表示第i个关节静摩擦系数;vsi表示第i个关节的Stribeck 速度;fbi为第i个黏滞摩擦系数.
2 非线性摩擦模型关键参数反求
在许多工程实际问题中如动力修改及优化、结构的强度分析、故障诊断和系统的健康检测等,一些关键参数通过理论分析和实验测量都很难直接获取,严重影响其在设计、建模、分析中的可靠性和安全性.工程反问题[39-40]通常利用容易测得的结构或系统的响应来反求难以通过实验或测量手段获取的关键参数.由式(7)可知,机器人的关节驱动力矩可以通过测电流的方式得到.因此,通过建立摩擦参数与机器人驱动力矩之间的关系,即可实现对摩擦参数反求.具体分析步骤如下:
(1)建立动力学模型,建立摩擦参数和驱动力矩之间的关系;
(2)分析摩擦参数对关节驱动力矩的敏感性,设计激励轨迹,增大摩擦参数对驱动力矩的敏感性;
(3)设置敏感摩擦参数的取值范围,即采样空间.在采样空间中进行采样,得到相应的关节驱动力矩响应值;
(4)建立包括摩擦参数样本和相应的关节驱动力矩的数据集.将得到数据集划分反问题神经网络的训练集、验证集和测试集;
(5)建立反问题神经网络;
(6)训练神经网络;
(7)对测试集误差进行分析.
2.1 机器人动力学建模
在恒速跟踪实验中,通过测量关节摩擦,得到关节摩擦模型和摩擦参数.但是随着工作温度、润滑油黏度、机器人使用时间的长短等因素,关节的摩擦参数也在不断发生变化.使用神经网络进行参数反求时,需要大量的数据样本,并且数据样本应尽可能覆盖实际参数空间的所有可能的取值,这将导致巨大的工作量和难以估量的计算量.因此通过建立机器人模型来代替真实机器人,来获得和摩擦参数相对应的驱动力矩,组成数据集.为了保证建立仿真模型和实际模型的准确性,可以对机器人进行动力学参数辨识[41],得到相对精确的动力学模型.
机器人运动学参数(用Denavit-Hartenberg 法描述)和局部坐标系如图5 和表4 所示,其中关节转角θi定义为从x i−1轴到xi轴的转角,绕z i−1轴正向转动为正.关节距离di定义为从x i−1轴到xi轴的距离,沿xi−1轴的指向为正.杆件扭角 αi定义为从z i−1轴到zi轴的转角,绕xi轴正向转动为正.杆件长度ai定义为从z i−1轴到zi轴的距离,沿xi轴的指向为正.在表5中,机器人动力学参数包括连杆的质量m、惯性张量Im和质心r相对于局部坐标系的坐标.对于协作机器人来说,减速器和轴承的重量相对于连杆来说非常小的,因此在建立动力学模型时忽略了减速器和轴承的重量.机器人关节2~ 4 的摩擦参数如表3 所示,对于其他关节,动态模型中没有加入摩擦特性.利用MATLAB 机器人工具箱(RTB)[42]建立机器人模型.

图5 六轴协作机器人Fig.5 Six axis cooperative robot

表4 连杆运动学参数Table 4 Kinematics parameters of links

表5 连杆动力学参数Table 5 Dynamic parameters of link
2.2 摩擦参数灵敏度分析
灵敏度分析是衡量输出响应对待反求参数敏感程度的关键,也是反问题计算成功的前提[43-47].若待反求参数一定,结构或系统的输出响应对待反求参数不敏感时,需调整边界条件等增加输出响应对待反求参数的敏感性或采用对待反求参数更为敏感的输出响应.若结构或系统响应已定,需要从相关参数中找到对结构或系统响应敏感的参数,然后对敏感的参数进行反求.鉴于本文是通过关节驱动力矩反求摩擦参数,所以为了选择对关节输出力矩敏感的摩擦参数,需要对式中可设计参数fsi,fci,vsi和fbi进行灵敏度分析.以关节3 为例,敏感性分析步骤如下.
(1)将关节3 的驱动力矩 τm3作为机器人在设计的笛卡尔轨迹下的响应.

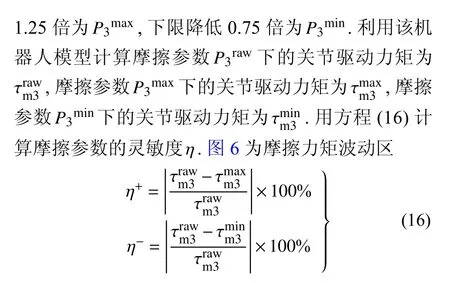
(3)通过对摩擦参数的灵敏度分析,选择灵敏度较高的参数作为需要进行辨识的参数.图7 为机器人规划的笛卡儿轨迹,是在XZ平面上从点 (−0.553 6,0.127 0)到点(−0.644 4,0.673 9)的一条直线轨迹.当关节摩擦参数为P3raw时,使机器人在这条直线轨迹上运动,同时得到关节3 的驱动力矩,采样频率为10 Hz,关节3 的驱动力矩如图8 所示.
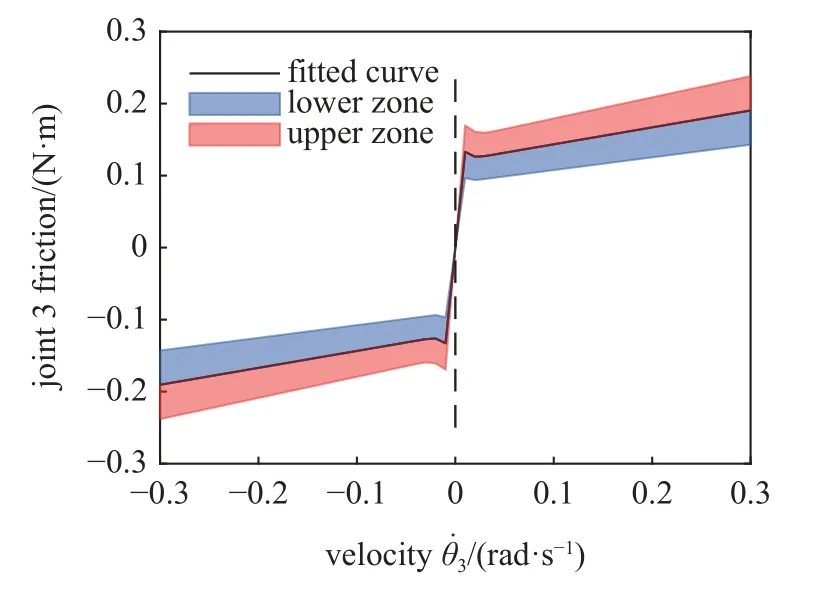
图6 关节3 摩擦波动区间Fig.6 Friction fluctuation zone of joint 3

图7 机器人的笛卡尔轨迹Fig.7 Cartesian trajectory of robot
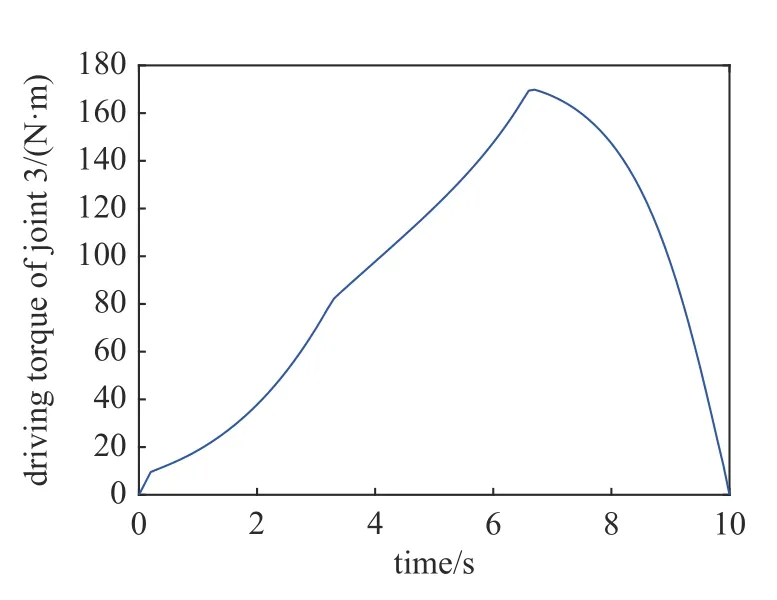
图8 关节3 的驱动力矩Fig.8 Driving torque of joint 3
灵敏度分析结果如图9 所示,是给定直线轨迹中4 个摩擦参数对驱动力矩随时间变化的灵敏度趋势.红线表示在摩擦参数P3max下对关节驱动力矩的灵敏度 η+.蓝线表示在摩擦参数P3min下对关节驱动力矩的灵敏度 η−.如图9(a)所示,库仑摩擦系数fc3的灵敏度 η+和灵敏度 η−绝对值最大值均为7.82%.如图9(b)所示,当t<2.3 s 或t>9.4 s时,静摩擦系数fs3的灵敏度 η+和灵敏度 η−的绝对值大于0,最大值为15.97%,其余部分的灵敏度是0.如图9(c)所示,黏性摩擦系数fb3的灵敏度η+和灵敏度 η−的绝对值均大于7.06%.如图9(d)所示,Stribeck 速度vs3的灵敏度η+和灵敏度η−的绝对值最大值分别为1.16%和1.68%.当2.3 s
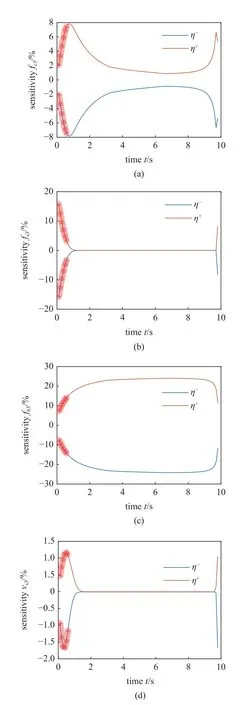
图9 摩擦参数对驱动力矩的敏感性分析Fig.9 Sensitivity of friction parameter to driving torque
2.3 关键摩擦参数反求
根据以上分 析,驱动力 矩 τmi对 这fci,fsi和fbi这3 个摩擦参数敏感,因此,选择它们作为需要反求的参数.涂骁[48]做了不同负载下的机械臂关节摩擦参数试验,发现摩擦参数会随着负载的变化而变化.为了使机器人在不同负载工况下,或者由于使用时间长造成摩擦参数变化的情况能快速得到反求得到准确的摩擦参数,取表6 所示的摩擦参数上下限作为采样空间,采用优化后的拉丁超立方法在3 个摩擦参数的采样空间内共获得了10 000 个样本.该方法为多个变量范围采样,极大的使变量范围的每一边缘分布分层,能够全面的覆盖到每一个变量范围.将这10 000 个样本代入机器人模型中进行计算,得到对应的关节力矩,进而得到一个完备的数据集,同时可以基于仿真模型和实际模型之间的误差,施加相应的噪声数据,来增强模型的泛化能力.然后,将数据集按照7:1.5:1.5 的比例划分为训练集、验证集和测试集.然后,根据训练数据集和需要反求的3 个摩擦参数建立逆神经网络.最后,利用训练数据集直接训练神经网络.
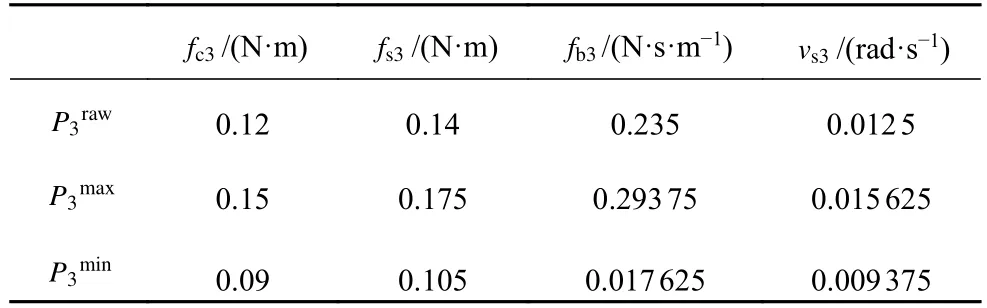
表6 关节3 摩擦参数的采样区间Table 6 Sampling interval of friction parameters of joint 3
2.3.1 建立神经网络模型
建立如图10 所示的BP 神经网络,输入层有6 个神经元,隐藏层有100 个神经元,输出层有3 个神经元.隐层神经元的数量由网络的可训练参数决定.由于有7000 组训练数据,神经网络具有很好的收敛性.取可训练参数与训练数据的比值接近于1.根据式(17)计算隐层神经元数为100

图10 神经网络结构Fig.10 Neural network structure

其中,N为神经网络的总层数,Di表示第i层输出神经元的数量.在建立了神经网络的基本结构后,选择tanh(18)作为激活函数.选取均方误差(MSE)Loss函数(19)作为神经网络的优化目标,该函数计算预测值与目标值差的平方和的均值.优化算法采用Levenberg-Marquardt 算法

2.3.2 反求结果
7000 组训练集用于训练,1500 组验证集用于验证,当验证集Loss 连续6 次不再下降时,就停止网络训练,避免过拟合,1500 组测试集用于测试.为了评价最终模型的泛化能力,测试集的数据与训练集的数据不一致.训练过程的Loss 曲线如图11 所示.神经网络需要多次迭代才能较好地拟合关节力矩和摩擦参数.当迭代次数达到500 时,Loss 有小幅度的下降趋势.当迭代次数达到1000 时,训练集的Loss 为 3.5034×10−9,验证集的Loss 为 3.6958×10−9,测试集的Loss为 3.6826×10−9.

图11 神经网络Loss 曲线Fig.11 Loss of neural network
由于测试数据集没有经过训练,所以可以用它来测试神经网络的泛化能力.如图12 所示.将所有测试集代入神经网络.反求结果与实际值的最大误差小于0.4%.摩擦参数预测的平均误差为:fs3>fb3>fc3.结果与第3 节中摩擦参数对驱动力矩的敏感性分析一致.即参数越敏感,反求的摩擦参数精度越高.其他关节摩擦参数反求误差如表7 所示.
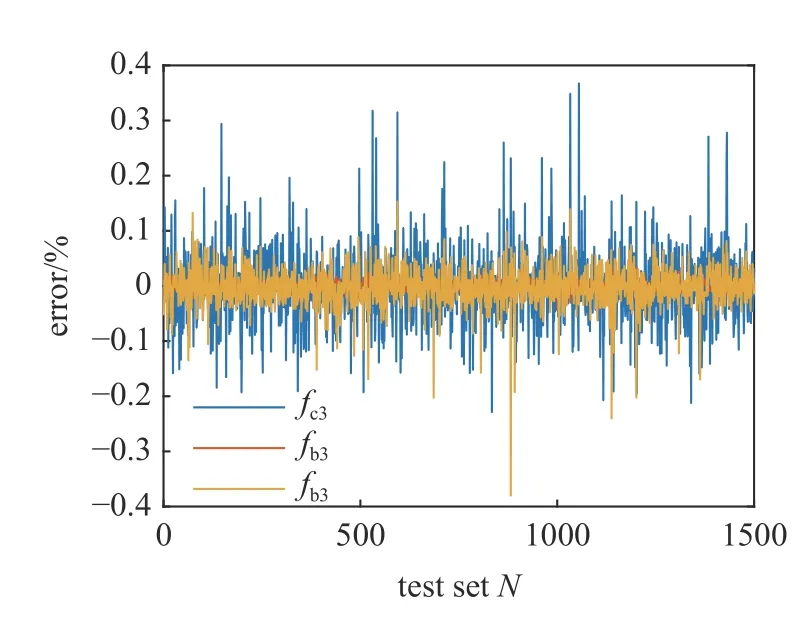
图12 测试集相对误差Fig.12 Test set relative error

表7 摩擦参数反求误差Table 7 Fricition parameter inverse error
3 实验验证
为了进一步验证神经网络反求参数的准确性,假设机器人负载发生了变化或者传动件长时间磨损导致摩擦参数变为原来的1.1 倍.使机器人在规划的轨迹上运动,同时测得机器人关节力矩,并把选取的力矩点的值输入训练好的神经网络,反求得到变化后的摩擦参数.
从表8 中可以看出,神经网络预测的参数精度很高,最大误差为0.36%.由这些参数建立的摩擦模型与机器人关节的实际摩擦力矩高度吻合.

表8 摩擦参数反求结果Table 8 Friction parameter inverse results
为了进一步验证用反求参数建立摩擦模型在摩擦补偿控制策略中能够减小关节摩擦的影响,提高机器人低速运行时的轨迹跟踪精度.因此,通过MATLAB,在Simulink 中建立如图13 所示的关节前馈控制系统.

图13 机器人关节前馈控制系统Fig.13 Feedforward control system for robot joints
因此,在仿真条件下,关节前馈控制律设为


下面将采用3 种方式做对比,一种是不带摩擦补偿的PD 控制,一种是用原始摩擦参数进行摩擦补偿的PD 控制和当摩擦参数变化后,通过神经网络反求的得到的摩擦参数进行摩擦补偿的PD 控制.以关节3 为例,在PD 控制律中Kp3=60,Kd3=30时进行研究,仿真结果如图14 所示,当没有摩擦补偿时,在关节速度换向时,摩擦力矩发生突变,导致关节速度发生突变,从而影响轨迹跟踪精度,造成巨大的位置误差,造成位置误差在在−0.05~ 0.03 rad之间.而当通过建立的摩擦模型使用原始摩擦参数进行补偿后,大大改善了机器人在低速换向时的速度突变问题,提高了速度跟踪和位置跟踪精度,使最大位置误差在0.01 rad 之内.而通过神经网络反求出的变化后的摩擦参数进行补偿后,跟踪误差和稳定性又得到了小幅度的提高.

图14 关节3 运动轨迹仿真Fig.14 Motion trajectory simulation of joint 3
4 结论
针对当机器人关节摩擦参数发生变化引起轨迹精度下降,精度维护困难问题,提出一种考虑时变效应的机器人关节非线性摩擦参数反求方法.通过构建机器人关节一般非线性摩擦模型,择取非线性摩擦模型关键参数,建立关节输出力矩和摩擦参数一一对应的数据集及反向神经网络模型,并对其进行学习与训练,实现非线性摩擦模型关键参数辨识与结果验证.研究的主要结论如下:
(1)通过设计实验,获得了机器人关节的非线性摩擦参数,建立了非线性摩擦模型;
(2)分析了摩擦参数对关节力矩的敏感性,对关节驱动力矩较敏感的非线性摩擦参数按照降序排列分别为fb,fs,fc和vs;
(3)所提的非线性摩擦参数反求方法具有较高的精度.反求的摩擦参数最大误差在0.4%以下,并且在仿真实验中表明,通过反求的参数建立的摩擦模型进行补偿,可以有效的解决在机器人关节速度换向时,摩擦力突变问题,提高轨迹跟踪精度;
(4)所提的非线性摩擦参数反求方法有效解决了机器人摩擦参数时变的难题,可以在机器人使用时间增长,摩擦参数不匹配时,通过一次测量同时识别多个关节的摩擦参数,提高识别效率,为机器人后期维护提供了方便快捷的解决方案.
