准周期响应对称破缺分岔点的一种快速计算方法1)

龚冰清 郑泽昌 陈衍茂 刘济科

(中山大学理论与应用力学系,广州 510275)

引言

周期或准周期振动,是非线性动力学系统出现的典型稳态响应[1-3].不同于周期振动,准周期响应不具有固定的振动周期,状态变量不再按某周期有规律地重复出现.更具体地说,准周期振动的特征是其振动频率由多个不可公约的频率线性组合而成[4-6].因而,这些不可约的频率也被称为基频,由不可约频率线性组合而成的准周期频率称为组合频率.

在不同的非线性系统中,准周期响应出现的机制机理也不尽相同.出现准周期响应的系统类型也是多种多样,例如,受到多不可约频率外激励作用的系统[7]、非线性耦合导致的模态共振[8]以及参数激振与自激振动之间的耦合[9]等情况都可能产生准周期响应.从振动的频率成分看,准周期振动可以看作是不可公约频率之间的耦合效应,而引起的复合响应.在实际工程中,准周期振动在各种科学和工程问题中均被大量报道,例如机械工程[10]、电子工程[11]、气动弹性[12]等领域.

在求解方面,数值方法由于简单明了且易于实现,因此被广泛运用于准周期响应的求解[13-15].这类基于时间离散的时程响应跟踪数值算法,一般无法直接获得系统的不稳定稳态解,即不稳定的周期或准周期响应.因为,不稳定解意味着微小的扰动或误差会使得解出现越来越大的偏差,从而偏离不稳定解本身.众所周知,系统的分岔通常会伴随着某些解的稳定性改变.为了进一步研究系统响应的分岔现象,研究人员提出了基于Fourier 级数展开的半解析半数值计算方法,用于求解周期响应,例如谐波平衡法[1]和增量谐波平衡IHB 法[16-19]谐波展开类方法、L-P 法和多尺度法等摄动类方法[1]、平均法和KBM 法等渐进方法[1]以及同伦分析法[20]等.这些方法有的也被改进或推广、用来求解准周期响应,其中多时间尺度IHB 法可以计算强非线性、多自由度系统,获得了广泛的应用.

关于系统的平衡点和周期解的分岔问题,目前已有大量的研究和成熟的理论,例如Hopf 分岔定理[21]和Floquet 理论[22]等.相较于平衡点分岔,周期响应的分岔计算是一个更加棘手的问题.20 世纪80 年代,陈予恕[1]提出了周期响应分岔计算的C-L 方法,并在诸多科学和工程中的非线性系统中得以广泛应用.在IHB 法中,若引入谐波系数限制增量过程,可直接求解周期响应倍周期分岔或对称性破缺的临界值[23].

对于准周期响应,其分岔计算方法和分析理论就更加棘手,也更加缺乏.目前来看,对于非线性动力系统的准周期响应,在大多数情况下,其分岔点的确定是通过反复的数值模拟来实现的.这种方法的原理简单、过程直接,但一方面计算量往往很大,另一方面如前面所述、数值方法也无法提供不稳定的解,而且存在不利于分析参数的影响规律等问题.为此,本文将周期响应对称破缺分岔计算方法[23]进一步推广,使之对于准周期同样有效,该方法是基于增量谐波平衡过程的.利用多时间尺度的IHB 法,设计迭代格式,通过追踪特定的谐波系数,从而快速求解准周期响应对称破缺分岔点.以多频激励Duffing系统以及Duffing-van der Pol 耦合系统为例,阐述方法的主要步骤,验证方法的正确性和有效性.

1 增量谐波平衡法

增量谐波平衡法是求解非线性振动问题的一种半数值、半解析方法,是由Lau 等[24]在20 世纪80 年代提出并发展起来的.IHB 法的本质是Newton-Raphson 增量过程和谐波平衡过程的结合[25].经过了几十年的发展,IHB 不仅可用于周期或准周期响应的求解,已应用于动力学响应分析的诸多领域,如混沌控制[26]、反问题识别[27]等.

考虑含不可约频率双外激励的非线性振动系统

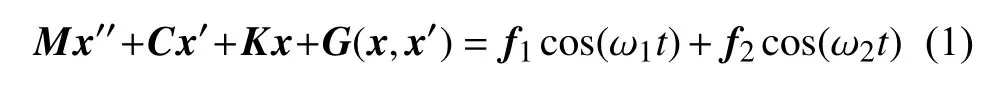
其中M,C,K分别是质量、阻尼和刚度矩阵,G(x,x′)是非线性函数.f1和f2是外激励向量幅值,ω1和 ω2是外激励的不可约频率.不失一般性,将参数 ω1作为分岔控制参数.

IHB 法的第一步是增量过程,即Newton-Raphson 过程.让xi表示一种振动状态,对应的控制参数为 ω1=ω1i,其临近状态可以通过增量的方式表示为

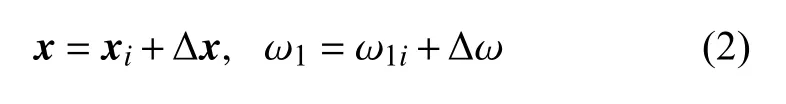
将式(2)代入式(1),展开并忽略高阶小量,得到线性化的增量方程

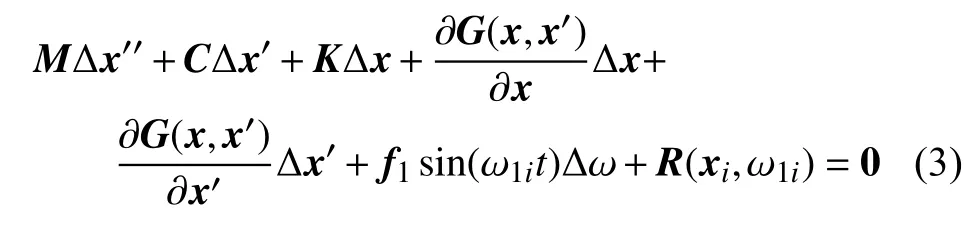
其中

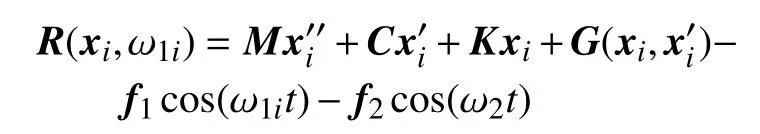
称为不平衡力,当xi和ω1i为方程(1) 的精确解时,R(xi,ω1i)=0.

IHB 法的第二步是谐波平衡过程,也即Ritz-Garlerkin 平均过程,令

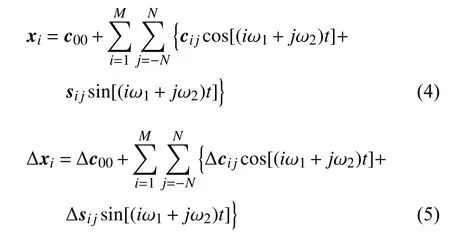
把式(4)和式(5)代入式(3),并应用谐波平衡过程,可以得到线性方程组

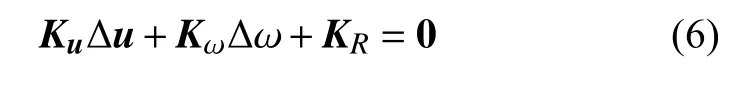
其 中 ∆u=[∆c0,∆c10,∆s10,···,∆cMN,∆sMN]T,方 阵Ku是 (M+N)(M+N+1)+1 维的雅可比矩阵,Kω是控制参数的梯度向量,KR是剩余向量.这些矩阵和向量可通过初始解xi和 ωi确定.在IHB 法中,通常应选择一个主动变化的参数(称为主动增量)来控制解的连续延拓.如果 ∆ ω 被给出,方程(6)描述的每一步增量为 ∆u的一组方程,可以迭代求解.

2 对称破缺分岔点的快速算法

下面引入补充方程,并将 ∆ ω 看成被动增量参与迭代,进而获得系统发生对称性破缺的分岔值.作为一般性的讨论,可将准周期解严格表示为广义的Fourier 级数

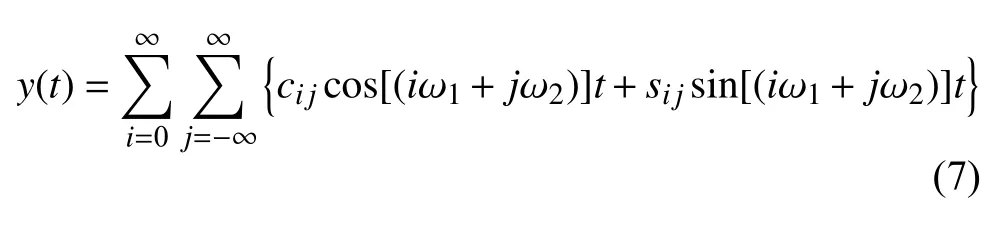
其中y(t)也可作为x(t)的一个分量.在实际计算中,对于单自由度系统,y(t)即是x(t);对于多自由度系统,y(t)可取为x(t)的第一个分量.对称的准周期响应的相图指的是,对于任意一点 (y(t),y′(t)),总能找到关于原点与之对称的点 (−y(t),−y′(t)).也即是表明,如果y(t) 是方程(1)的解,那么 −y(t) 也是一个解.

引入双时间尺度 τ1=ω1t和τ2=ω2t,和周期解对称性质类似[23],对于关于原点对称的准周期解,其对称性由以下等式描述

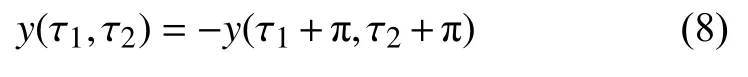
由式(7),可知

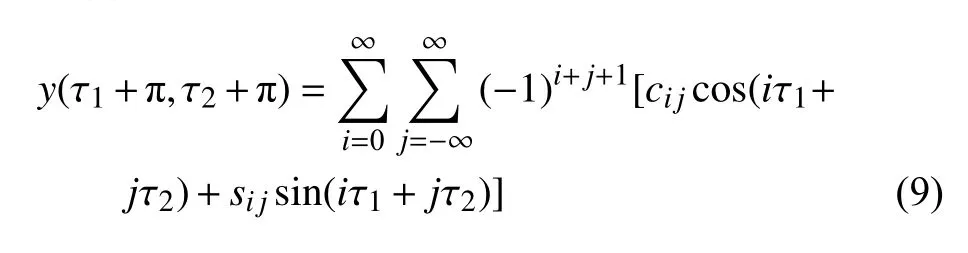
根据方程(7)～方程(9)可知,当i+j为奇数时,对称条件自然满足;当i+j为偶数时,若要满足对称条件,则意味着

注意到i+j的奇偶性和 |i|+|j| 相同.那么,当偶次谐波系数取到非零的小量时,准周期解便失去对称性,也可以看成是系统发生对称破缺分岔的临界状态.为此,在迭代格式(6)中,补充方程

其中 0 <λ0≪1,那么通过迭代过程,构造以下迭代格式

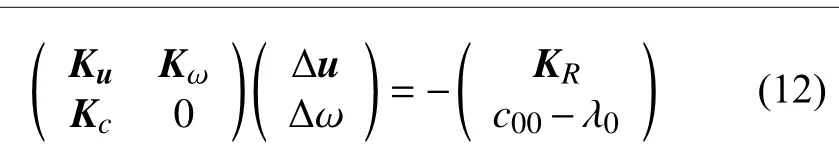
其中Kc=(1 0 ··· 0) 是补充方程(11) 关于谐波系数的Jacobi 矩阵.只要 λ0足够小时,便可以近似确定关于参数 ω1的对称破缺分岔点.理论上,λ0越小则 ω1越可能接近真实的分岔值.在实际计算中,可以取 λ0为非常小的正数,例如λ0=1.0×10−8等.当然,最终的近似程度也还受到解的截断谐波系数的影响.这点在下面的算例部分将予以讨论.

3 结果验证与讨论

首先,考虑含不可约频率双外激励的Duffing 振子系统[20,28-29]

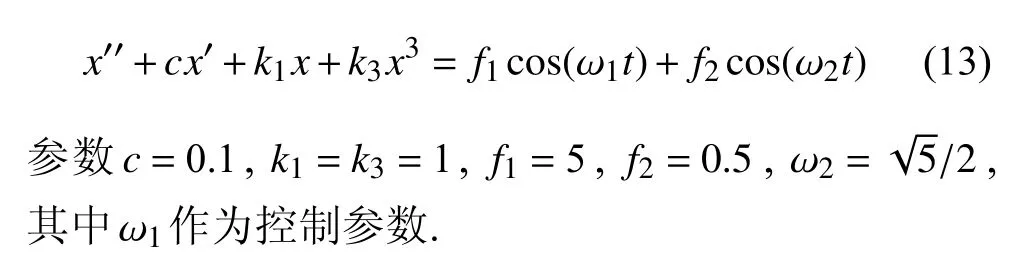
图1 是所考虑Duffing 系统的准周期响应相图,其中图1(a1)～图1(c1)为IHB 法结果,图1(a2)～图1(c2)为4 阶Runge-Kutta (RK)法结果.在求解过程中,IHB 解截取了最高阶M+N=10 阶谐波,数值解采用了IHB 解作为初始条件,通过RK 法积分获得.准周期解的稳定性判别目前还是一个非常棘手的问题.一般的数值积分方法如RK 法和Newmark 法等无法追踪不稳定解,通过这一直观特点简单判断解的稳定性.分别对比图1(a1)、图1(a2)(ω1=0.8)及图1(c1)、图1(c2)(ω1=1),IHB 结果与RK 结果是完全吻合,说明这些准周期解都是稳定的.进一步观察到,在图1(a1)中,准周期响应相图是关于原点中心对称的,因此是对称的.

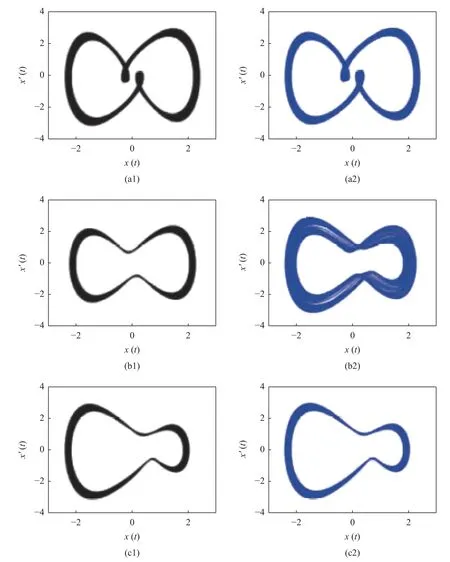
图1 Duffing 系统(13)准周期响应相图,(a1) ω1=0.8,稳定IHB 法解;(b1) ω1=1.0,不稳定的IHB 法解;(c1) ω1=1.0,稳定的IHB 法解;(a2),(b2),(c2)为相应的RK 数值解.其中,IHB 法的截取谐波数为 M+N=10Fig.1 The quasi-periodic responses of Duffing system (13).(a1) Stable with ω1=0.8,(b1) unstable with ω1=1.0 and (c1) stable with ω1=1.0,all obtained by the IHB method with the truncated number of harmonics as M+N=10 ;(a2),(b2),(c2) the corresponding solutions provided by the RK method

当 ω1=1.0 时,而图1(b1),图1(b2)中的结果并不完全相同.其中,由IHB 法解作为初始值所得的RK法结果(图1(b2)所示),从对称的IHB 法解(图1(b1)所示)开始,逐渐收敛到另一个非对称的准周期解,即图1(b2)所示非对称部分.实际上,图1(b2)所示的非对称部分、在相图上和图1(c1)及图1(c2)所示解是一样的.IHB 法是半解析半数值方法,可以得到不稳定的对称准周期解和稳定的非对称准周期解.由此可知系统在参数范围 0.8<ω1<1.0 发生了对称破缺分岔,且对称的准周期解失去了稳定性.

为准确找到系统发生对称破缺的分岔点,根据上述方法,将 λ0逐步减小,得到收敛结果,其中 ω1的变化如图2 所示.随着 λ0的取值越来越小,ω1的值也逐渐收敛.当谐波数取M+N=8 时,可以计算得到分岔值约为0.933 02,当谐波数取M+N=10 时,可以计算得到分岔值约为0.937 58.

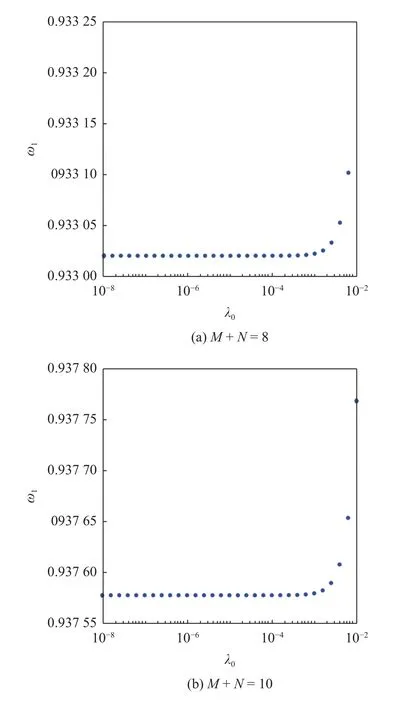
图2 采用不同的 λ0 所对应的对称破缺分岔点Fig.2 The symmetry breaking point predicted by the presented method with different value of λ0

图3 是由IHB 法获得的Duffing 系统准周期响应的分岔图.在P点(约为 ω1=0.935)附近,对称的准周期解产生非对称的分支.此时,系统出现了对称破缺分岔现象.和周期解分岔类似,经历了分岔后、准周期解也一般会稳定性改变.周期解的稳定性一般可通过经典的Floquet 理论准确判别[1].然而,对于准周期解,其稳定性判别是一个相当棘手的问题.为此,通过分析系统稳态响应的相图变化,如图1 所示,进而直观地判别IHB 法所得结果的稳定性.研究发现,对称准周期响应由于对称破坏而失去稳定性,同时出现的非对称解是稳定的.

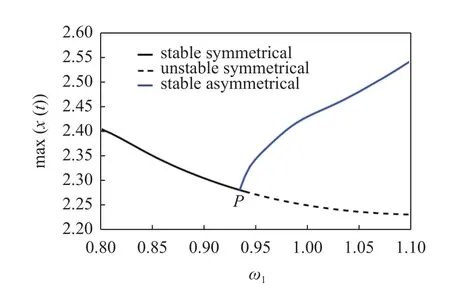
图3 由IHB 法获得的Duffing 系统(13)准周期响应分岔图,其中P 为对称破缺分岔点Fig.3 The bifurcation chart of the quasi-periodic response of Duffing system (13),where P denotes the symmetry breaking point

进一步,用数值法验证准周期响应对称破缺的发生.图4 给出由RK 法得到的解的最大和最小振幅随 ω1的变化图.可以观察到,在 ω1=0.937 5 前,准周期解的最大值和最小值完全重合,即解是对称的;而随着 ω1增大,最大值和最小值之间逐渐出现差值.也即是表明,系统已经失去了对称性,并且大约在ω1=0.937 5 时发生了对称破缺分岔.这也与IHB 法结果基本是一致的.

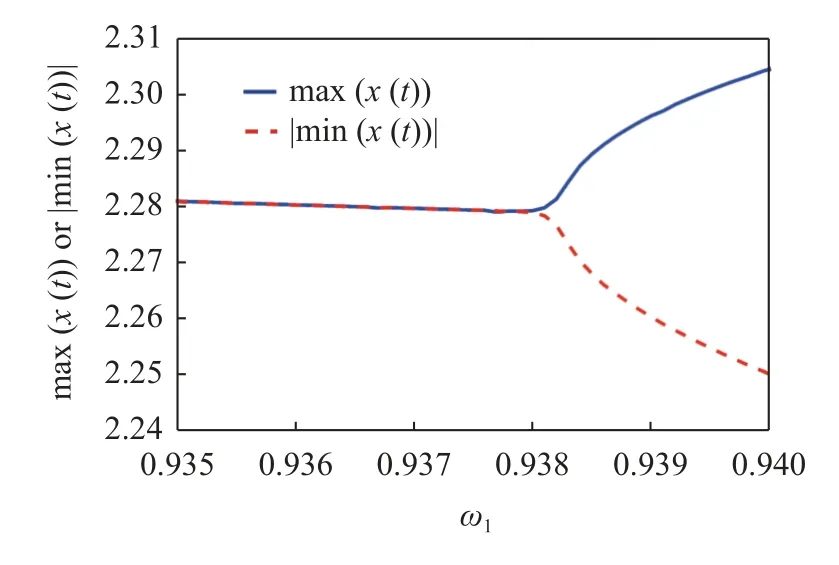
图4 RK 法所得Duffing 系统(13)稳定的准周期解的最大和最小振幅变化图Fig.4 The maximal and minimal of the amplitude of the stable quasiperiodic response of Duffing system (13),provided by the RK method

图5 给出了分别由快速Fourier 变换和IHB 法获得的准周期响应频谱图.首先,IHB 法结果和数值结果吻合良好.数值结果的部分峰值没有IHB 法结果与之对应,因为IHB 法中组合谐波进行了截断,取了M+N=7,即 |i|+|j|≥8 的组合谐波没有包含在IHB 法结果中.当参数取 ω1=0.937 时,图5(a)所示,响应只包含奇数次谐波成分.对应于解的表达式(7),出现了当 |i|+|j| 是奇数(即1,3,5,7 等)时的若干谐波成分.当参数为 ω1=0.938 时,除了占主要部分的奇数次谐波之外,还出现了幅值较小的偶数次谐波,图5(b)所示的 2 ω1,即i+j=2.图6 是准周期响应的频率谱瀑布图,由此可更直观地观察到,当参数 ω1逐渐增加,响应出现了偶次谐波成分.根据基于关系式(8)～式(10)的讨论,偶数次谐波分量的出现,表明准周期响应逐渐失去了对称性.由此推断,对称性破缺分岔点出现在0.937 和0.938之间.

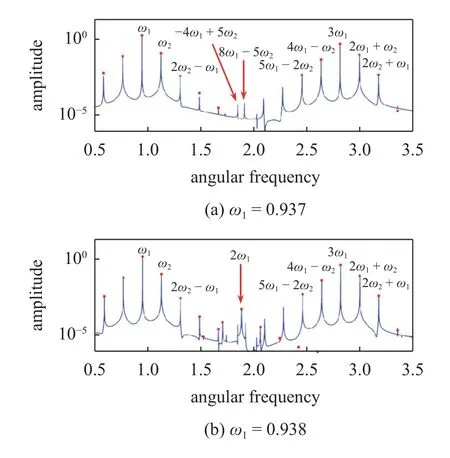
图5 由快速Fourier 变换得到的Duffing 系统(13)准周期响应的频谱图,其中蓝线是数值方法结果,红点是IHB 法结果,组合谐波截断数为 M+N=7Fig.5 The FFT spectrum for the quasi-periodic response of Duffing system (13),where the blue line denotes the numerical result and red the IHB result,with the number of truncated harmonics as M+N=7

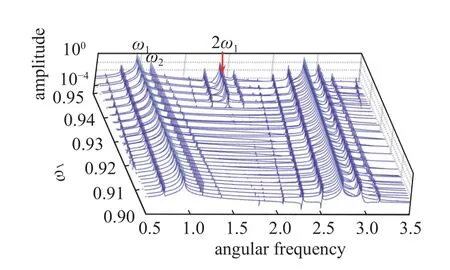
图6 Duffing 系统(13)准周期响应的频率谱瀑布图Fig.6 The frequency waterfall for the quasi-periodic response of Duffing system (13)

Duffing 系统和van der Pol 系统都是典型的非线性振动系统.由它们耦合组成的多自由度系统,更是蕴含了丰富的动力学行为,是非线性研究广泛采用的模型之一[30-31].为了进一步检验所提方法的有效性,考虑Duffing-van der Pol 耦合振子

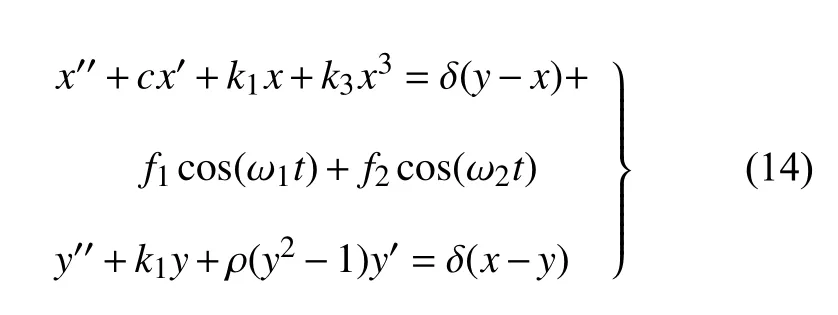
其中,Duffing 振子受双谐波外激励,参数选择和系统(13)相同;耦合系数取 δ=0.2 ;ρ=1 是van der Pol振子的非线性系数.

对于含强非线性环节的van der Pol 系统,一些依赖于小参数的摄动类方法有时难以获得准确的周期或准周期解.由于不依赖于小参数,IHB 和同伦分析等方法对含van der Pol 振子的强非线性系统有效,因而被广泛采用[20,31-33].

图7 给出了本文算法所得的分岔值与预设小量λ0之间的关系.当 λ0逐渐减小时,所得分岔值快速收敛于固定值,约为1.000 4.图8 所示准周期响应的最大和最小振幅,当 ω1超过1 且接近1.001 时,最大和最小振幅出现了微小的偏差.这表明,在此参数区间,响应逐渐失去了对称性,也即是出现了对称性破缺分岔,验证了计算结果的准确性.

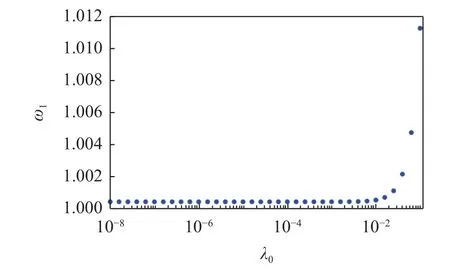
图7 Duffing-van der Pol 系统(14)的对称破缺分岔值关于 λ0 的收敛图,其中截取谐波数为 M+N=8Fig.7 The symmetry breaking point predicted by the presented method with different value of λ0,with the number of truncated number of harmonics as M+N=8 for Duffing-van der Pol system (14)

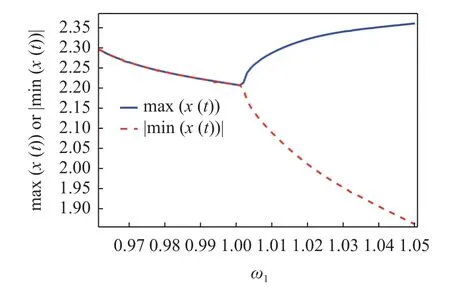
图8 RK 法所得Duffing-van der Pol 系统(14)准周期解的最大和最小振幅Fig.8 The maximal and minimal of the amplitude of the stable quasiperiodic response of Duffing-van der Pol system (14),provided by the RK method

4 结论

本文基于IHB 法,提出了一种快速计算准周期响应对称破缺分岔的方法.方法的基本依据是,当发生对称破缺分岔前,准周期响应的某些谐波系数为0;发生分岔的过程中,这些系数逐渐变为非0 的小量.那么,依据这一性质,在IHB 法迭代格式中,预先令某个谐波系数为给定的小量,可以将控制参数视为被动变量,通过收敛的IHB 法结果,直接获得响应的分岔值.

研究了含不可公约频率双外激励Duffing 振子系统、以及Duffing-van der Pol 耦合系统,验证了所提方法.结果表明,方法能准确得到系统准周期响应的对称破缺分岔点,得到了数值法结果的验证.本文方法不仅可以找到不稳定解,更重要的是可以直接提供控制参数,而不需要反复的跟踪和试错过程.