双稳态压电俘能器的簇发振荡与俘能效率分析1)

2022-12-18钱有华陈娅昵

力学学报 2022年11期

钱有华陈娅昵

(浙江师范大学数学与计算机科学学院,浙江金华 321004)

引言

能量俘获(energy harvesting)是通过一定的方法从环境中提取能量的过程.众所周知,环境中存在着各种形式的振动能[1],如海上的巨浪、机器的工作、车辆的行驶、人的运动、乐器弹奏等都会产生大量振动.这些振动不会受到地域、时间等的制约,通过收集振动能可用于桥梁[2]、建筑、车辆等健康监测.

目前振动能量收集主要有三种方法: 电磁式[3]、静电式[4]以及压电式[5-7]等,其中运用较多的是压电式.它的原理是将一层(单晶)或者两层(双晶)压电材料附着于某种夹持结构(悬臂梁)上,外部环境激励通过基座传递给悬臂梁,使梁产生弯曲变形,该形变使得压电材料中的正负电荷分离,产生电势差,从而进行能量收集.收集能量之后,还需要通过整流桥和滤波电容器将交变电压转化为整流电压,以此进行充能.

线性压电俘能器只在共振频率附近能够收集到较多能量,其有效工作的频率带宽很窄.为了拓宽系统的工作带宽,人们设计了多种方案来改善线性压电俘能器.如阵列式,多自由度等.与线性技术相比,非线性技术可以在更大的连续频率带宽上输出较大电流,从而提高能量收集的效率.非线性来源主要包括结构变形、外加非线性力等.Moon 等[8]最早提出双稳态结构是由悬臂梁及梁的自由端附近对称放置的永磁体组成.其耦合动力学可用负刚度Duffing 方程来描述,此时系统存在两个稳定平衡点,一个不稳定平衡点.Erturk 等[9]讨论了系统处于高能轨道和混沌振动时对输出电压的影响.Stanton 等[10-11]研究了磁斥力双稳态动力系统,发现磁间距能够使得系统在单稳态、双稳态之间变化,并且双稳态系统中包含有单势阱内运动、双阱间混沌运动、双阱间大幅周期运动等.高鸣源等[12]建立分数阶阻尼模型,通过实验揭示了多稳态电磁俘能系统的动态分岔、势能阱逃逸、高能态轨道和混沌运动等非线性行为.田海港等[13]基于非定常气动力模型,推导翼型颤振压电俘能器流−固−电耦合的数学模型并制作了压电俘能器样机来验证仿真结果.曹东兴等[14-15]建立了一种附磁阶梯变厚度压电悬臂梁的动力学模型并分析了系统的俘能特性,研究了流致振动,设计了一种附加磁力激励的压电悬臂梁流致振动俘能器.张伟等[16]利用可移动铰支座和非线性磁力设计了一种具有双稳态特性的宽频压电俘能器使得其与环境相匹配.郭纪元等[17]提出一种线绳驱动、具备转速提升功能的电磁式俘能器,实验验证了所能收集到的能量.陈楠等[18]总结了面向压电振动俘能器的电能管理电路的最新研究成果.Andreas 等[19]实现了可穿戴的电子设备设计,提出了超柔性铁电聚合物和有机二极管结合的俘能器,使得脉搏和血压监测更加精确.

在双稳态压电俘能器的研究中,很多学者发现了低频激励下存在着簇发振荡现象,也被称之为跳变现象[20].簇发振荡是一种复杂的振荡模式,它的特征是小幅振荡与大幅振荡的结合.Rinzel[21]最先提出了冻结子系统的方法来解释簇发振荡.Izikevich[22]在他的工作中对簇发振荡的类型进行了分类.Qian等[23-24]利用快慢分析方法对欧拉离散后的系统进行分析,发现了丰富的动力学行为.Chen 等[25]分析了具有周期激励的耦合振荡器,它会在静息态与激发态之间发生簇发振荡.Lin 等[26]研究了简单的三元记忆电路,并在电路信号中得到了簇发振荡.Han 等[27-29]通过快慢分析法研究了不同时间尺度下的动态响应问题,还发现了时滞周转引起的新的簇发振荡类型,叉式翻转迟滞簇发振荡以及复合叉式迟滞簇发振荡,还分析了集中参数式俘能器的动力学簇发振荡.Jiang 等[30-34]分析了不同类型俘能器的簇发振荡以及复杂动力学行为.马新东等[35]对三维非线性电机系统进行分岔分析,并得到了时滞subHopf/fold cycle簇发振荡,焦点/焦点型对称式叉形分岔滞后簇发振荡等.郑健康等[36]在三维混沌系统中引入参数激励并分析了其簇发振荡.

由于低激励下压电俘能器的理论的研究较少,因此,本文试图从高低能轨道的角度来揭示俘能效率.先分析双稳态压电俘能器在较高频率下的动力学特性,再考虑低频环境下不同势阱对系统簇发振荡现象的影响,同时分析了其俘能效果.最后还考虑了环境中存在多个振动源时,系统的动力学行为和俘能效果.

1 双稳态压电俘能器的动力学分析

压电俘能器通过非线性恢复力产生大变形,它可以由结构的大变形产生,也可以由外加的非线性力产生等.Ertuk 等[9]设计了磁铁−梁结构的压电俘能器(如图1).这个结构中,梁具有弹性恢复力且梁的末端与两侧磁铁之间有磁力作用,当系统受到简谐激励时,梁会在两个磁铁之间不停地摆动.

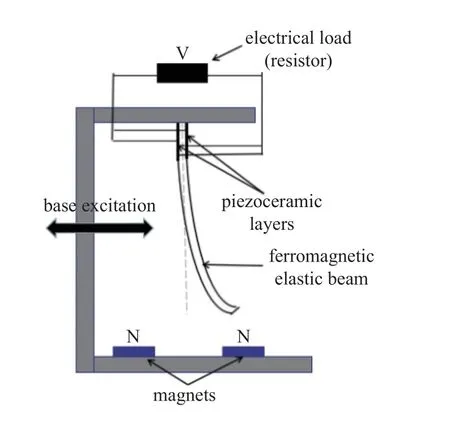
图1 双稳态压电俘能器结构示意图Fig.1 Structural diagram of bistable piezoelectric energy harvester

在以往的研究中,基于建模方法和实验测量,俘能器的一般控制机电模型可以写成下式[9]

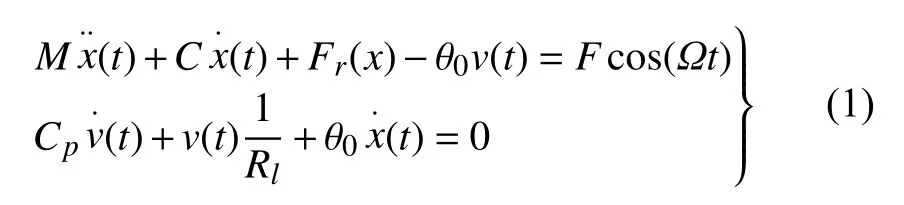
其中,x(t)是相对于基座的尖端位移;M是等效质量;C等效阻尼;Cp,Rl,θ0分别是等效电容、负载电阻和等效机电耦合系数.v(t)是通过Rl的输出电压.Fcos(Ωt)为等效外激励.Fr为等效非线性恢复力,包含线性恢复力和非线性磁力.为了使得系统出现双稳态现象,选取Fr=−ω02x+a10x3.并将系统进行无量纲化

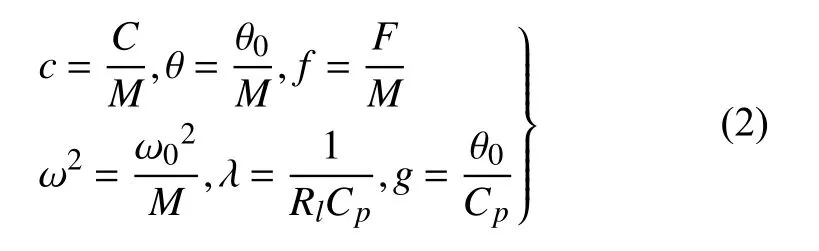
推导出以下无量纲模型

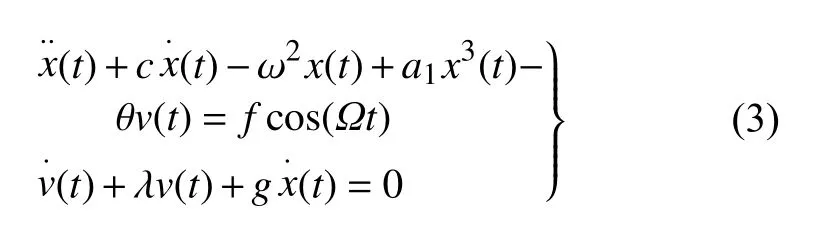
令 γ=fcos(Ωt),当 γ 变化时系统会表现出丰富的动力学行为.当c=0.65,ω2=1,a1=1,θ=0.05,f=0.8,λ=0.05,g=0.5时,可以得到系统外激励频率变化的分岔图.

图2表示当Ω取不同的值时,系统会出现周期运动或者混沌运动.例如Ω<0.8 附近时,系统呈现单极限环运动,而当0.8<Ω<1.1附近时,系统大部分呈现混沌运动,接着当1.1<Ω<1.45附近时,系统表现出三极限环运动,随着Ω继续增大,系统又出现了混沌运动.

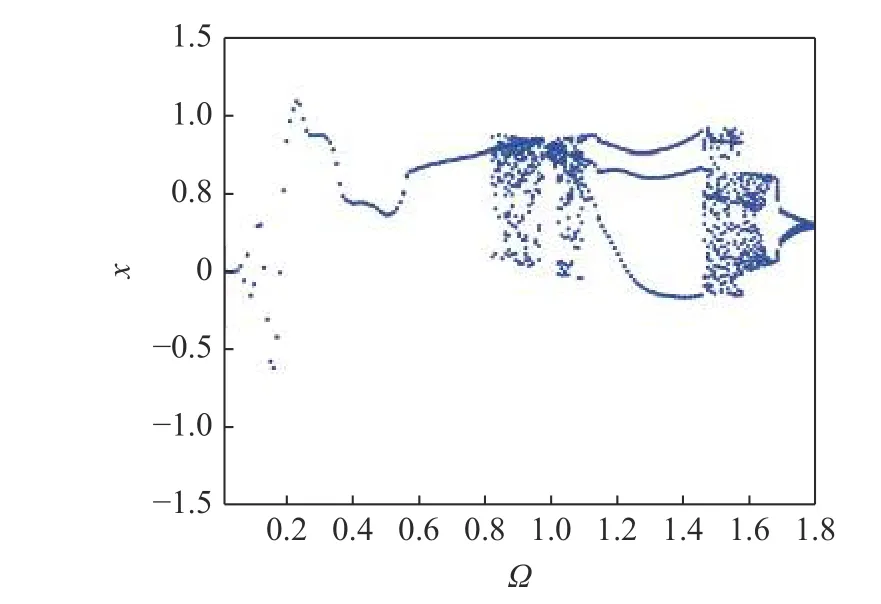
图2 当c=0.65,ω2=1,a1=1,θ=0.05,f=0.8,λ=0.05,g=0.5时系统的分岔图Fig.2 Bifurcation diagram of the system with c=0.65,ω2=1,a1=1,θ=0.05,f=0.8,λ=0.05,g=0.5

除此之外,当频率一定,外激励强度变化,会使系统处于不同的轨道上,包括阱内周期运动,阱内混沌运动,阱间周期运动,阱间混沌运动等.Paula 等[37]表示不同的轨道对系统能量收集效率的影响是显著的.给定其他参数不变,当Ω=1.5,f=0.6,0.7,0.716,0.75时系统的相图见图3,其中横纵坐标均为−2～ 2.

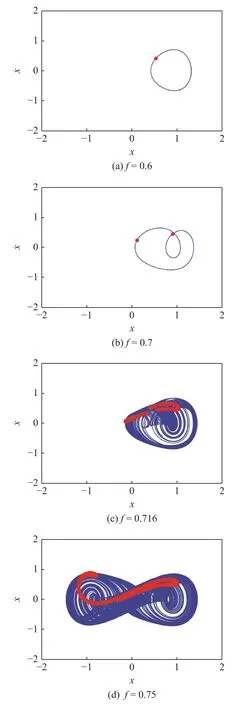
图3 当 Ω=1.5 时不同振幅下系统的相图,红点表Poincaré映射点Fig.3 When Ω=1.5,the phase diagrams of the system with different amplitudes,and the red dots represent Poincaré maps

可以看出,当振幅比较小时,系统只在某个势阱内作周期运动,随着f的逐渐增大,系统开始在单势阱内做混沌运动,到了f=0.75时,系统在两个势阱之间作混沌运动.随着f的不断变化,系统会在周期运动和混沌运动之间摇摆.Lyapunov 指数图也可以说明系统的混沌运动,图4 中的红色表示0,当Lyapunov 指数大于0 时有混沌运动.

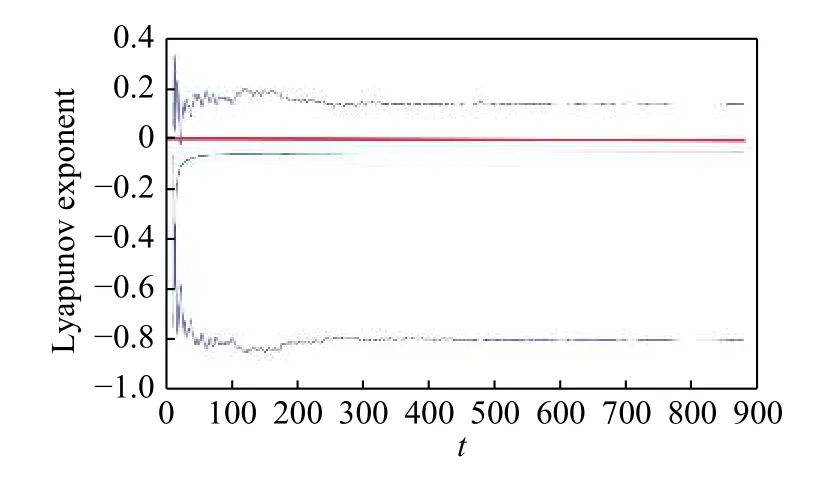
图4 当 c=0.65,ω2=1,a1=1,θ=0.05,f=0.8,λ=0.05,g=0.5,Ω=1.5时系统的Lyapunov 指数图Fig.4 Lyapunov exponent diagram of the system with c=0.65,ω2=1, a1=1,θ=0.05,f=0.8,λ=0.05,g=0.5,Ω=1.5

对于双稳态系统来说,它最大的优势就是拓宽了系统高效收集能量的频率带宽,可以在一般频率中找到高能轨道从而提高能量收集效率.选择c=0.05,ω02=1,a1=1,θ=0.05,λ=0.05,g=0.5以及f=0.1,0.2,0.5,计算一段时间内的输出电压均值(图5),这可以作为系统在不同频率下俘能效果的一个指标.

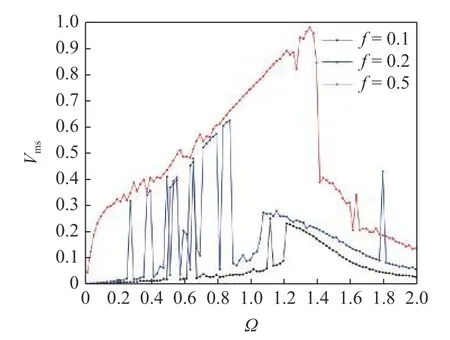
图5 当 c=0.05,ω02=1,a1=1,θ=0.05,λ=0.05,g=0.5 以及f=0.1,0.2,0.5时,系统输出电压均值图Fig.5 When c=0.05,ω02=1,a1=1,θ=0.05,λ=0.05,g=0.5 and f=0.1,0.2,0.5,mean value diagram of system output voltage

从图5 可以看到,当f=0.1 时,系统只在共振频率附近有着较高的电压输出,而在大部分频率下都只有低能输出.随着f的增大,系统在 Ω∈(0.2,1) 之间的输出电压比f=0.1 时有着较大的提高,这可能是获得了高能轨道导致的.随着f继续增大,系统的输出电压在整体上有了较大的提高,这是因为振幅的增大使得系统更容易获得高能轨道.值得注意的是在 Ω∈(0.01,0.1) 之间,系统的输出电压相比起前两者也有了一个明显的提高,下面会详细解释这一现象的原因.

2 单激励下双稳态压电俘能器的高能轨道与俘能效率

在实际生活中,低频率的振动源处处存在,例如海浪、人体运动等.在双稳态压电俘能器的研究中,可以发现它在低频激励下表现出簇发振荡现象,而单稳态压电俘能器却没有这种现象.簇发振荡指的是系统在某一时刻突然发生极大的振荡,此时的能量也是巨大的.下面先进行势能分析,再考虑不同振幅的影响.

2.1 势能分析

单稳态俘能器的特征是具有全局最小的单势阱,此时势阱图上表现为结点;双稳态俘能器的特征是具有两个势阱,并且这两个势阱被局部最大值分隔,从极小值到极大值的这段距离也称为势垒,此时势阱图上存在两个结点,一个鞍点.图6 给出了双稳态系统存在的两种运动形式,单势阱内的低能振荡和双势阱间的高能振荡.

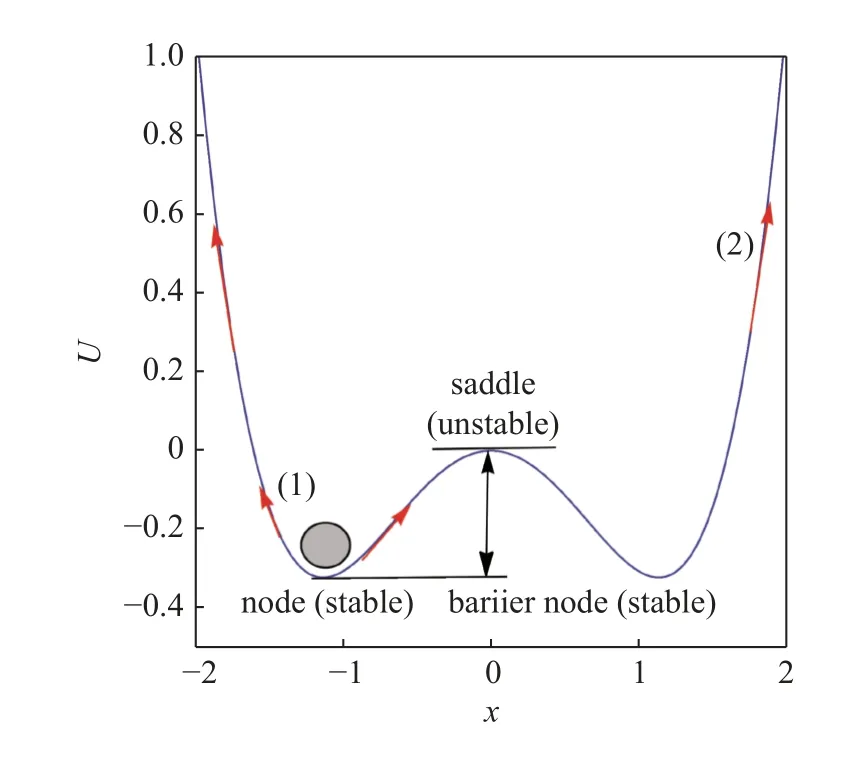
图6 低能阱内振荡和高能阱间振荡Fig.6 Low energy well oscillation and high energy inter well oscillation

现在考虑式(4),当环境频率很低时,也就是 Ω远小于固有频率,此时 γ 为慢变量,系统含有两个时间尺度.对于该系统,它的势能函数为

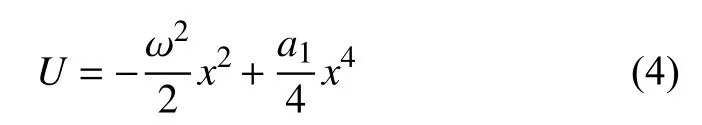
2.2 相同势阱下不同振幅的影响

取c=0.05,ω2=1,a1=0.778,θ=0.05,Ω=0.01,λ=1,g=1.首先考虑系统在平衡点 (0,0,0) 处的情况.

随着 γ 的改变,当f满足一定条件,例如f=0.5时,式(3)的平衡点个数会在三个和一个之间变化.此时系统表现出静息态和激发态之间的跃迁.系统在短时间内可以达到很大的能量,如图7 所示.

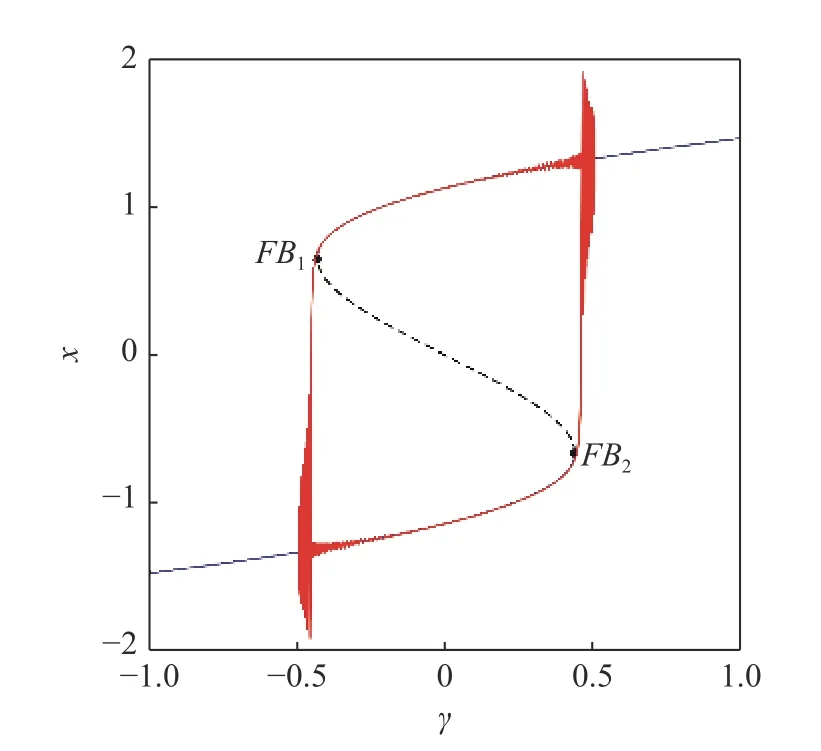
图7 当 Ω=0.01,f=0.5 时系统发生簇发振荡时的转换相图Fig.7 Transformed phase diagram of bursting oscillation whenΩ=0.01,f=0.5

同时这很好地展示了双稳态现象,系统的上分支与下分支实线部分分别是两个稳态,对应于图6中向下的两个阱,而虚线部分对应于图6 中的狭窄高地.当 γ 经过两个分岔点之间时,系统处于双稳态现象,而一旦越过分岔点,就会发生跳变,从一种状态跃迁到另一种状态.

从转换相图上来看,系统一个周期内的运动先后经过了两次尖峰振荡.尖峰振荡在开始时表现出巨大的能量,然后慢慢减弱直至进入静息态,接着进入负半周期,在负半周期里也发生了类似的过程.事实上,系统大幅振荡的原因是因为碰到了分岔点.开始时系统在上分支沿着左侧移动,到达FB1后,突然从上分支跳跃到下分支,并进入尖峰振荡,随着系统继续左移,尖峰振荡减弱,在到达−0.5 后,系统开始向右运动,直至进入弛豫振荡,一直到系统再次碰到分岔点FB2,系统从下分支跳跃到上分支,重新进入尖峰振荡,类似上半周期,这样就完成了一整个周期的运动.

但是,若f=0.4,系统不会出现簇发振荡现象,而只是简单的作周期运动.如图8.

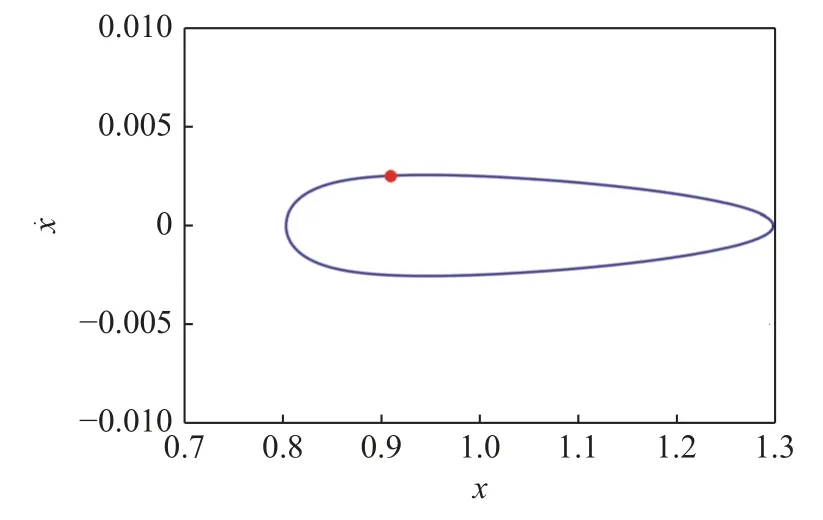
图8 当 Ω=0.01,f=0.4,系统发生周期振荡时的相图,红点表示Poincaré映射点Fig.8 Phase diagram of periodic oscillation when Ω=0.01,f=0.4,red dot represents Poincaré point

将两者进行对比,可以看到系统周期振荡时极限环非常小,纵坐标大约在 ±0.01 内.这也就暗示着系统在f=0.4下产生的能量远小于f=0.5.可以理解为: 当f=0.4 时,系统不能实现上下分支之间的跳跃,只能局限在上分支或者下分支上,此时它只能在单个势阱中做低能阱内运动.而f=0.5 却使得它实现了上下分支之间的跃迁,此时它获得了高能阱间振荡轨道.图9 可以很好地表示系统在不同振幅下的轨道分布.

图9 不同振幅下系统的轨道分布,黑色表示势能函数,蓝色圆圈表示 f=0.4,红点表示 f=0.5Fig.9 The orbit distribution of the system under different amplitudes.Black represents potential energy function,blue circle represents f=0.4 and red point represents f=0.5

下面探究继续增大f,是否会获得更高的能量.图10 给出了不同f下输出电压的时间历程图.

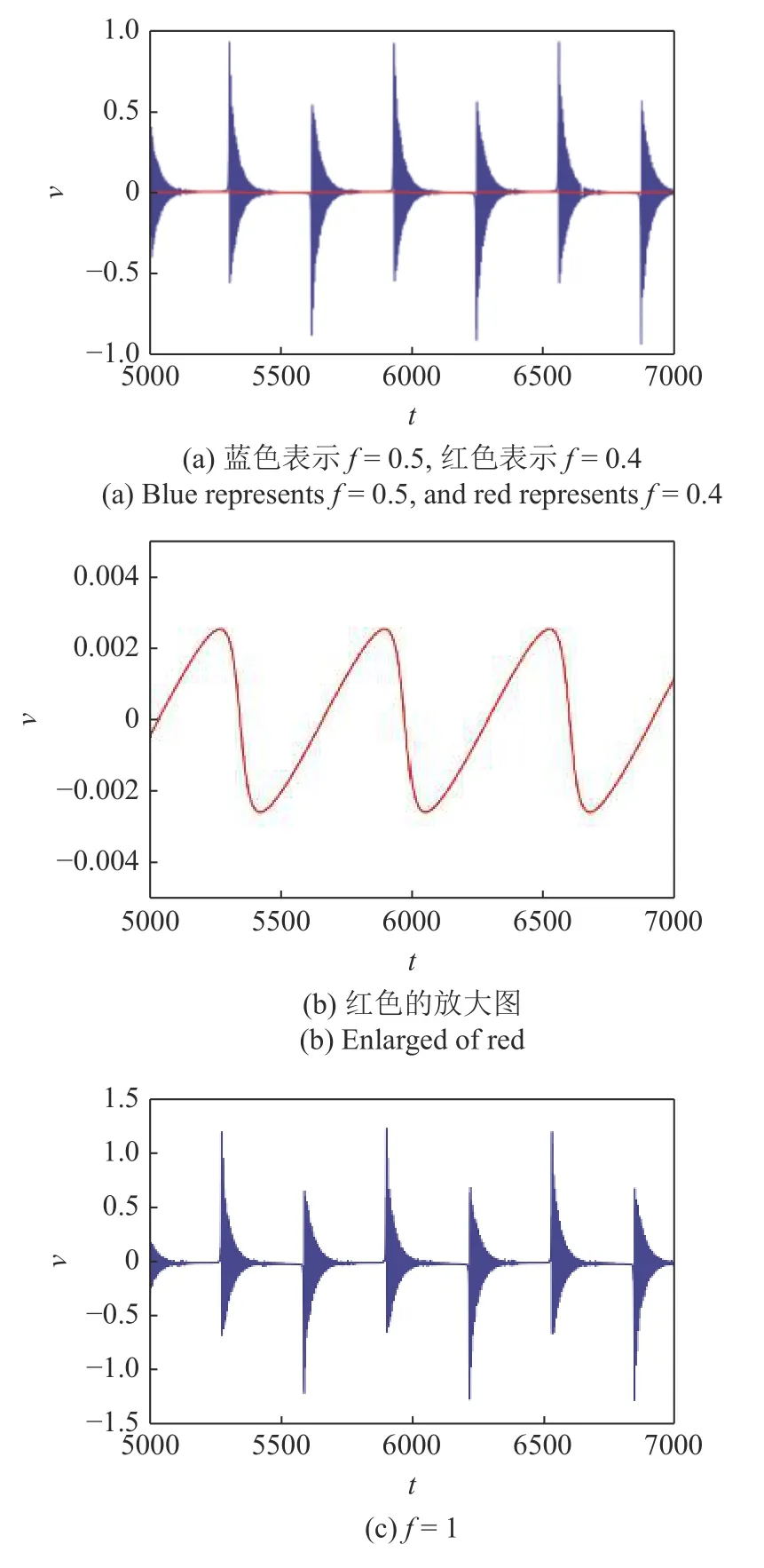
图10 当 Ω=0.01 时不同振幅下俘能器输出电压的时间历程图Fig.10 Time history diagram of output voltage of energy harvester under different amplitude with Ω=0.01

在图10(a)f=0.5 时输出电压大约在 ± 1 间,而低能轨道上的输出电压近乎为一条直线,图10(b)是局部放大图,虽然也有振荡,但是此时振荡的振幅非常小,大约在 ± 0.02 上下,能量收集效率低下.而图10(c)给出了当f=1 时系统的输出电压,与图10(a)进行对比发现两者输出电压的时间历程图非常相似,最高输出电压也近乎一样,接近于1.这就说明了增大系统的振幅并不能收集到更高的能量.事实上,在这种情况下,系统处于同一条高能轨道,对于同一条高能轨道而言,输出电压的上限也大致相同,振幅的改变能够使得系统获得这个高能轨道,而不能改变输出电压的上限.

2.3 势阱深浅对输出电压的影响

再分析势阱的深浅是否会对能量收集产生影响.选择第二组数据a1=1.667,ω2=1 以及第三组数据a1=0.778,ω2=1.4,其他参数保持不变.与第一组数据相比,分别改变了 ω2和a1,改变这两者都可以实现势阱深度的变化(图11).

图11 不同势阱对比图.红色表示 a1=1.667,ω2=1,蓝色表示a1=0.778,ω2=1,黑色表示 a1=0.778,ω2=1.4Fig.11 Contrast diagram of different potential wells.Red represents a1=1.667,ω2=1,blue represents a1=0.778,ω2=1 and black represents a1=0.778,ω2=1.4

选择f=1,选择较大的振幅是为了确保这三组情况下的系统都能产生簇发振荡.对比v(t) 的时间历程图,可以发现较深的势阱确实会影响输出电压,见图12.

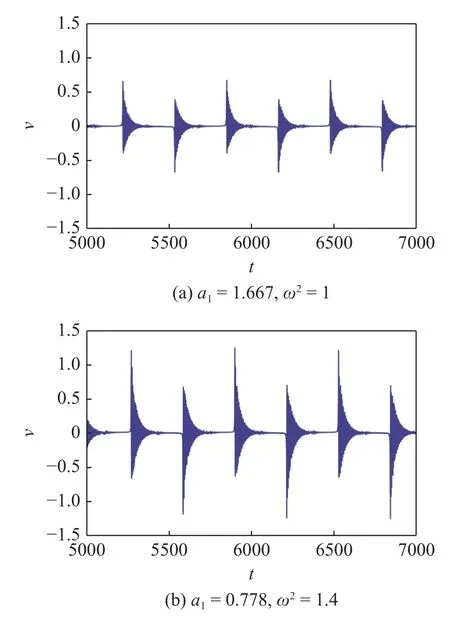
图12 当 f=1 时不同势阱下俘能器输出电压的时间历程图Fig.12 Time history diagram of output voltage of energy harvester under different potential wells with f=1

将图12 与图10(a)进行比较,注意两者坐标轴的不同.图12 的纵坐标都在 ± 1.5 间,而图10(a)的坐标在 ± 1 间.且图12(a)对应红色势阱,势阱深度最小,它的输出电压的最高值接近0.7;图10(a)对应蓝色势阱,它的输出电压最高接近1;而图12(b)对应黑色势阱,此时势阱深度最大,它的输出电压最高可达1.2.可以看出势阱越深,能够达到的最高输出电压就会越大,但同时,随着势阱加深,系统所需要的外激励振幅也要相应地增大才可以获得阱间高能轨道.对于红色势阱来说,它的势阱最浅,因此只需在振幅达到f=0.3 就可以获得高能轨道;对于蓝色势阱来说,它要在振幅达到f=0.44 时才可以获得高能轨道;而黑色势阱由于其势阱的深度,它的振幅至少要达到f=0.73 才可以获得高能轨道.

由此看来,在某些低频环境里若振幅普遍较大,那么可以通过设计含有深势阱的压电俘能器来获得更高的能量,但是若在某些环境中,振幅普遍较小,设计含有浅势阱的双稳态压电俘能器是一种非常好的选择,它可以通过簇发振荡直接实现输出电压量级上的提升且对振幅要求很低.

2.4 俘能效果分析

俘能效果受到磁铁间距、悬臂梁的结构阻尼比以及负载电阻等的影响.在悬臂梁结构参数、磁铁物理参数等确定的情况下,ω2,a1的影响磁铁距已在2.3 中进行了分析.这一部分主要探究悬臂梁的结构阻尼,负载电阻对俘能效果的影响.为了更好地对俘能效果进行评价,选择一段时间内的平均功率作为衡量指标.

2.4.1 等效阻尼比对俘能效果的影响

悬臂梁等效阻尼比c的大小主要与悬臂梁的材料和固定端夹持条件有关.若悬臂梁的材料阻尼系数比较大,或者夹持段预紧力太大,会限制悬臂梁实现阱间大幅振荡;若悬臂梁的材料阻尼系数或夹持段预紧力太小,悬臂梁在高频或者高激励下振动容易失稳损坏.

保持 Ω=0.01,ω2=1,a1=0.778,θ=0.05,f=0.5,λ=1,g=1 不变,分别选择c=0.01,0.05,0.3 进行对比.c=0.01,0.3 输出电压的时间历程图为图13.

将图13 与图10(a)进行比较,纵坐标都为 ± 1,可以看到阻尼比越小,系统的输出电压越密集,随着阻尼比的增大,尽管系统的簇发振荡行为还在,但其激发态的时间明显缩短,而静息态的时间越来越长,而希望的能量收集大多集中在激发态,因此这并不利于收集能量.当c=0.3 时,系统大部分时间都处于静息态,此时的能量收集效率是非常低的.

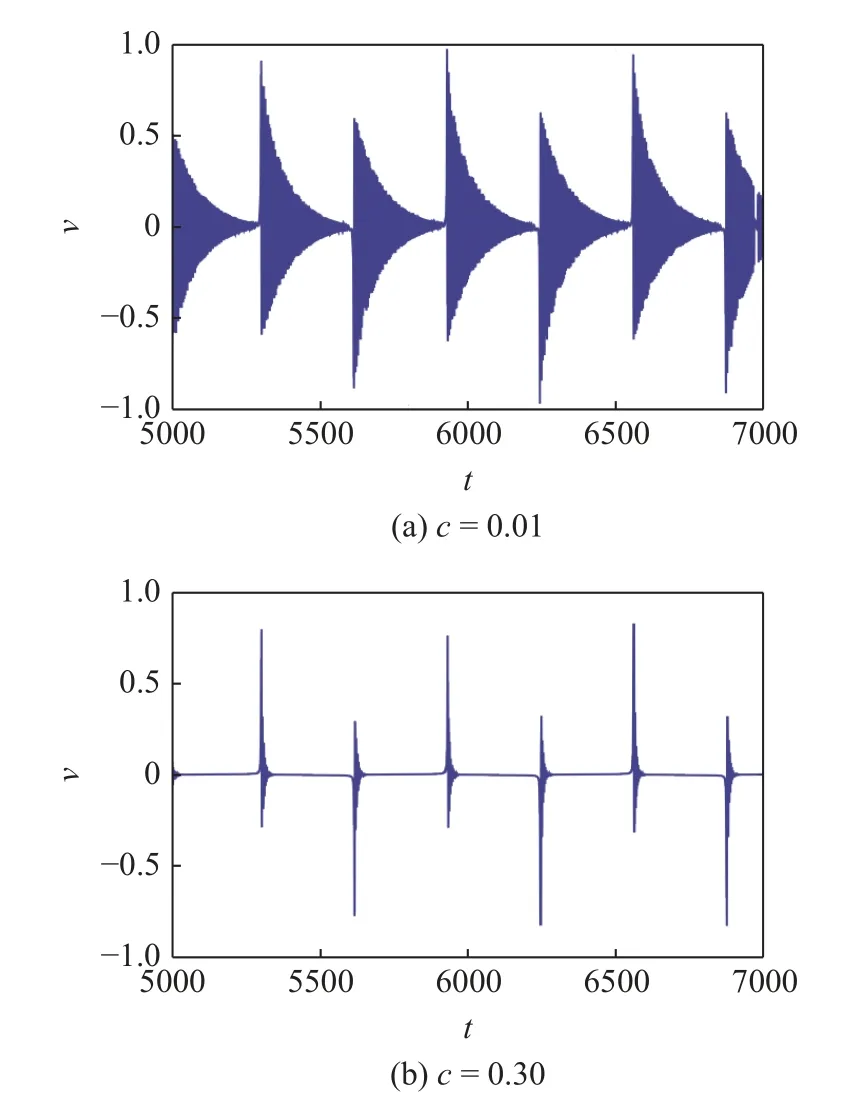
图13 当 Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f=0.5,λ=1,g=1时不同阻尼比下俘能器输出电压的时间历程图Fig.13 Time history diagram of output voltage of energy harvester under different damping ratio with Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f=0.5,λ=1,g=1

从图14 中也可以看出,随着阻尼比的变化,俘能器的输出电压逐渐降低,并且开始时输出电压的下降速度最快,而后慢慢趋于平稳.在阻尼比较大时,俘能器的输出电压低于0.02.比较三者阻尼比之间的输出电压关系,可以得到当c=0.01 时,系统输出电压接近0.134 9;当c=0.05 时,系统的输出电压接近0.056 3;当c=0.3 时,系统的输出电压只有0.011 4,此时的输出功率接近于0.由此可以发现在c∈(0,0.05)时,俘能器的能量收集效率较为理想.随着阻尼的增大,系统收集效率越来越低.同样地,输出功率与阻尼的关系也会表现出类似的变化规律.

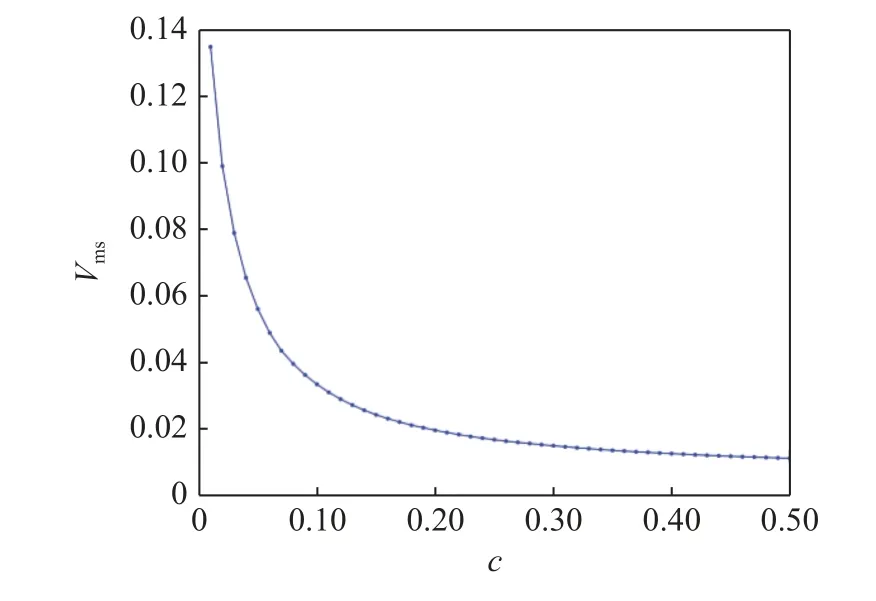
图14 当 Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f=0.5,λ=1,g=1时不同阻尼比下俘能器输出电压均方根变化图Fig.14 When Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f=0.5,λ=1,g=1,the output voltage diagram.of energy harvester with different damping ratio

2.4.2 负载电阻对俘能效果的影响

在C p不变的情况下,若Rl逐渐增大,会导致 λ 减小,对于式(3)这个系统来说,λ 的减小会使得输出电压增大,而输出功率又受到输出电压与负载电阻的共同影响.下面给出输出功率随负载电阻的变化图(图15).

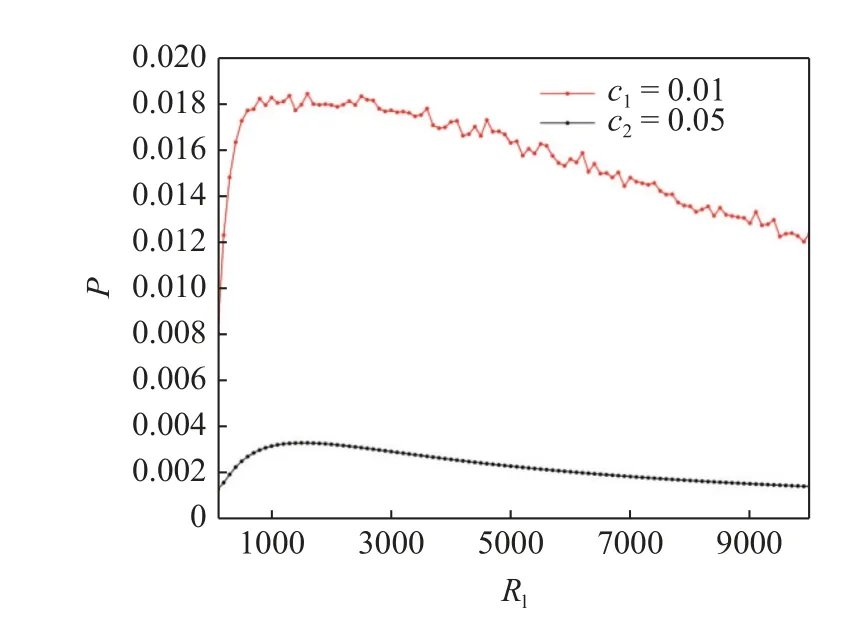
图15 当 Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f=0.5,g=1 时俘能器的输出功率随负载电阻变化图Fig.15 When Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f=0.5,g=1,the output power diagram.of energy harvester with different load resistance

当c=0.01,0.05 时,随着负载电阻Rl的不断增大,俘能器的输出功率均呈现出先上升后下降的特点.并且,当c=0.01 时系统输出功率是波动下降的.从图15 中可以看到,当c=0.01 时,系统的输出功率最高能达到约0.018,而当c=0.05 时,系统的输出功率最高不超过0.004.这验证了之前的猜测.

同时,为了使系统的输出功率达到最大,还需要匹配最优电阻,此时最优电阻应该在1000～ 2000之间.

3 多频激励下双稳态压电俘能器的簇发振荡

实际环境中往往会出现多个振动源的情况.这些振动源可能有着不一样的频率,此时系统受到多频激励的作用,如果它们的频率比接近整数倍而振幅又满足一定的关系时,会出现多条高能轨道.文章中考虑的振动是相互独立的.

3.1 动力学分析

假设两种频率的比例接近2.系统可将两个慢变量转化为只包含一个慢变量.

重新将 γ 记作 γ=cos(Ωt).取 Ω=0.01,ω2=1,a1=0.778,θ=0.05,f1=0.2,λ=1,g=1,c=0.05,分别取f2=0.4,0.6,0.7.此时输出电压的时间历程图如下.

红色方框表示的是一个周期内的运动,可以看到当f2=0.4 时,系统的输出电压在−0.004～0.004间近乎为0.而图16(b,c)纵坐标都在−1～1 之间.当f2=0.6时,系统只进行了一次簇发振荡,簇发振荡后面紧跟着的是普通周期振荡,由于振幅极小,看上去像是一条直线.不一样的是当f2=0.7 时,系统的簇发振荡骤然增多,红色方框内的运动实际包含了两次簇发振荡,尽管这两次簇发振荡看上去很接近,但是左侧的两支连接的略微紧密,而右侧的两支进入静息态的时间似乎更长.

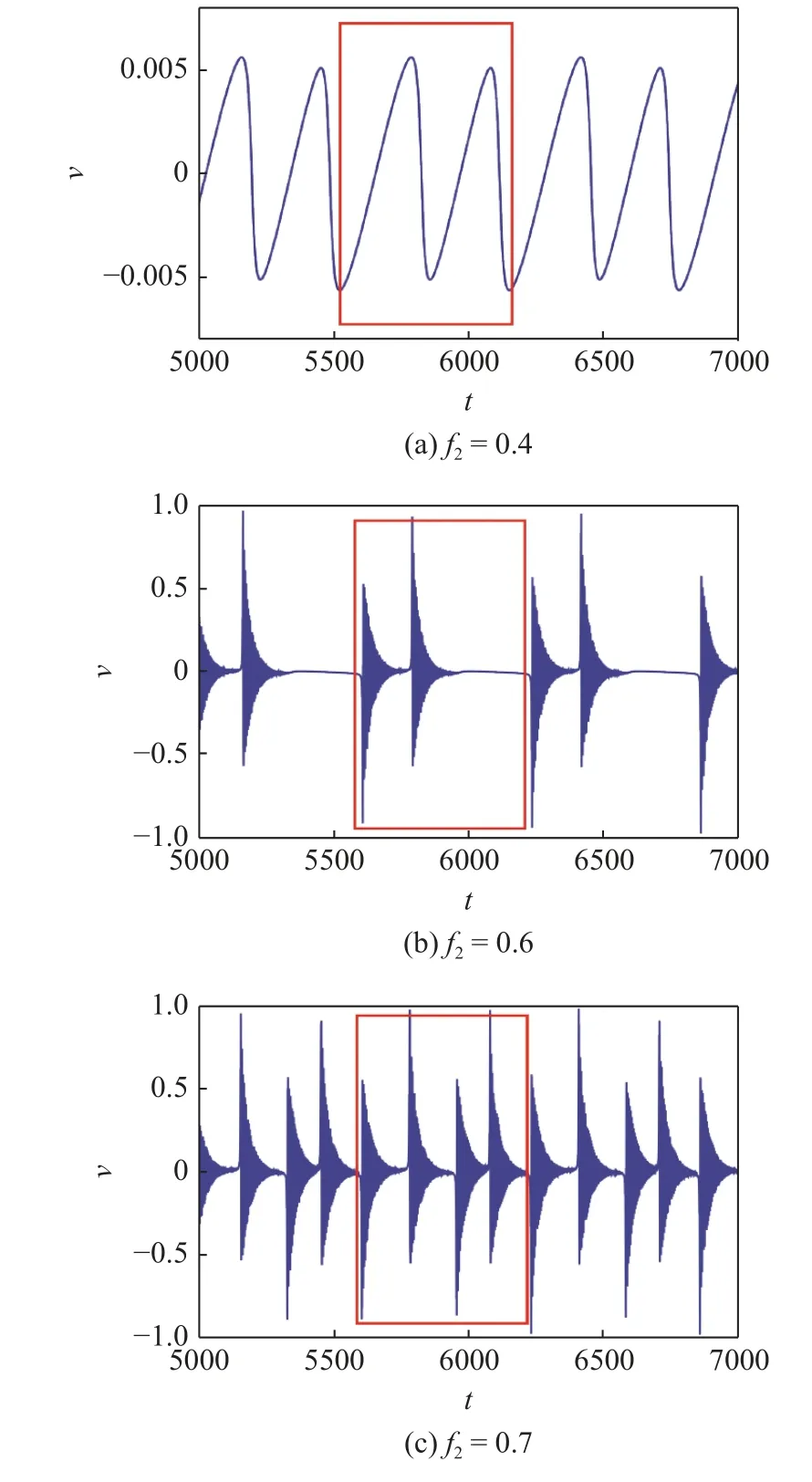
图16 当 Ω=0.01,c=0.05,ω 2=1,a1=0.778,θ=0.05,f1=0.2,λ=1,g=1 时,不同 f2 下俘能器输出电压的时间历程图Fig.16 When Ω=0.01,c=0.05,ω 2=1,a1=0.778,θ=0.05,f1=0.2,λ=1,g=1,time history diagram of output voltage of energy harvester under different f2

图17 中给出了分岔图以及它的运动轨线,蓝色实线表示稳定,黑色虚线表示不稳定,并且此时分岔图中存在四个分岔点F B1,F B2,F B3,F B4.假设系统在右上分支运动,它沿着分岔曲线向左移动,在遇到F B3后,突然从上分支跳跃到下分支,并开始大幅振荡.系统沿着下分支逐渐左移,振荡开始减弱,接着进入弛豫振荡状态,直到到达分岔点F B2,它突然从下分支跳跃到上分支,又一次开始大幅振荡,继续向左移动,直到−1 后反向向右移动,遇到F B1又重新进入大幅振荡,继续向右移动,振荡减弱,再遇到了FB4才会进入大幅振荡.此时这四次跳跃构成了一个周期的运动.

图17 当 Ω=0.01,c=0.05,ω 2=1,a1=0.778,θ=0.05,f1=0.2,f2=0.7,λ=1,g=1 时系统的转换相图,蓝色实线表示稳定,虚线表示不稳定Fig.17 When Ω=0.01,c=0.05,ω 2=1,a1=0.778,θ=0.05,f1=0.2,f2=0.7,λ=1,g=1,transformed phase diagram of system,blue solid line represents stability,dotted line represents instability

显然,此时系统通过双外激励能够获得两条高能轨道.通过对外激励振幅的控制,可以实现低能阱内振荡、低能阱内振荡与高能阱间振荡的组合,两条高能阱间振荡的组合等.

可以看到在f2=0.6 时,系统获得了一条高能轨道,一条低能轨道.通过外激励的作用,系统会依次经过高低能轨道.因此在图18(b)的一个周期中,剧烈振荡表示的就是高能轨道,而后半周期微小的振荡(由于振荡非常微小所以被压缩成一条直线)表示的则是低能轨道.当f2=0.7,得到了两条高能轨道,区分这两条高能轨道并不容易,那是因为高能轨道一般在最高点处才表现差异,只有系统在两次簇发振荡中能够达到的最高点有明显的差异,才容易观察到不同的高能轨道.而现在,系统的两次振荡形状过于接近,特别是在最高点时,也只有毫厘差距,显示出的高能轨道也非常接近.

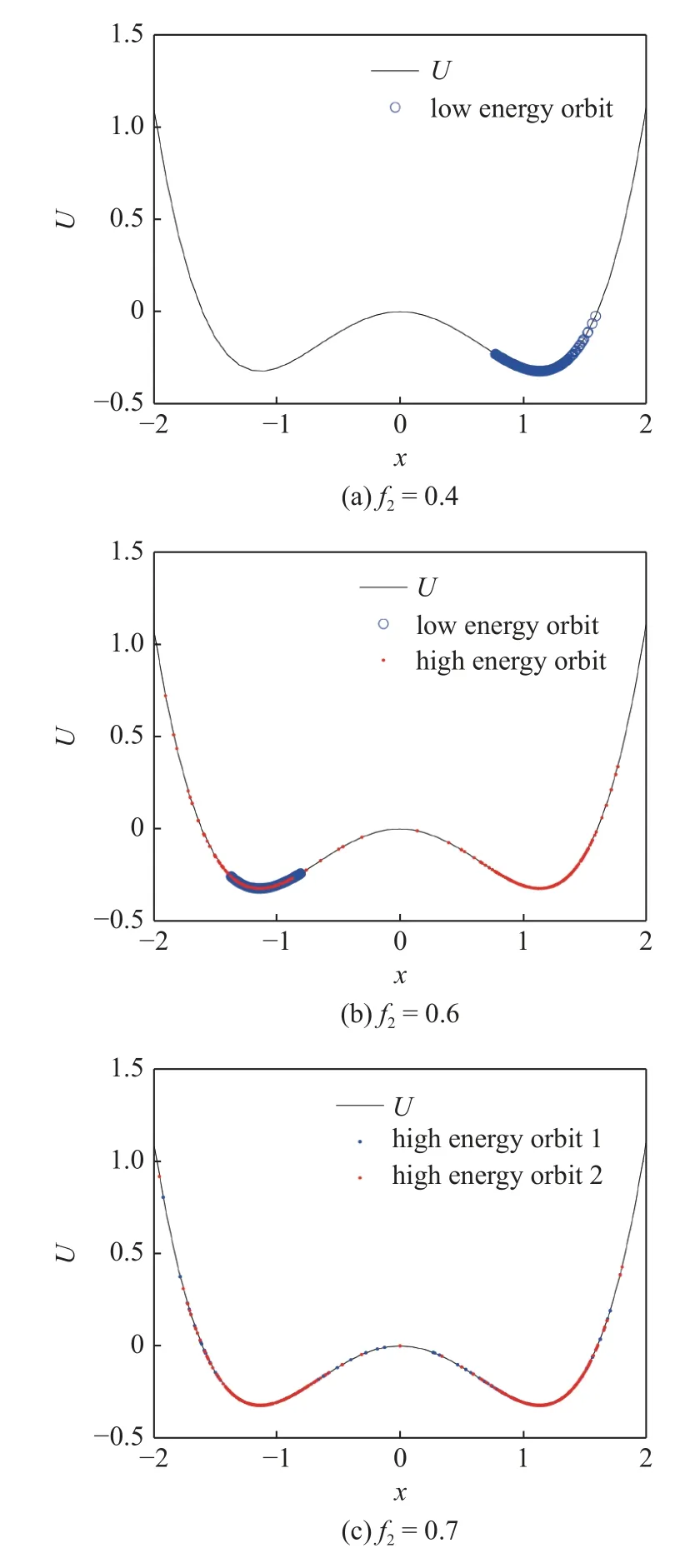
图18 当 Ω=0.01,c=0.05,ω 2=1,a1=0.778,θ=0.05,f1=0.2 时系统的轨道分布Fig.18 When Ω=0.01,c=0.05,ω 2=1,a1=0.778,θ=0.05,f1=0.2,the orbit distribution of system

3.2 俘能效果分析

这一节来研究多条高能轨道对俘能效果的影响.图19 为双稳态压电俘能器输出功率随负载电阻的变化图.为了说明高能轨道在收集能量方面的高效率性,分别考虑三种情况,f2=0.4,0.6,0.7.

图19 当 Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f1=0.2,f2=0.4,0.6,0.7时输出功率随等效负载的变化图Fig.19 When Ω=0.01,ω 2=1,a1=0.778,θ=0.05,f1=0.2,f2=0.4,0.6,0.7,the output power diagram of energy harvester with different load resistance

与单个激励项的压电俘能器进行比较,可以得到大致的趋势是类似的.图19 从横向来看,随着负载电阻的增大,系统的输出功率先增大后减小.此时可以匹配较优的负载电阻,大约是1000～3000.纵向来看,当f2=0.7 时,系统得到两条高能轨道,此时最高输出功率接近0.012,远高于f2=0.6 时系统的最高输出功率(不超过0.004).而没有高能轨道的f2=0.4的最高输出功率已经接近于0,此时系统的俘能效果最差.