基于改进复声强法的非合作跳频信号方位估计

王哲睿，王 燕，王逸林，董文峰

（1.哈尔滨工程大学 水声技术重点实验室，哈尔滨 150001；2.海洋信息获取与安全工信部重点实验室（哈尔滨工程大学），工业和信息化部，哈尔滨 150001；3.哈尔滨工程大学 水声工程学院，哈尔滨 150001）

跳频通信具有很好的抗干扰、低截获以及多址组网等能力，并在水声通信系统中得到广泛应用[1-3]。在实际环境中，通常具有多个通信节点同时工作，即跳频通信组网。对通信对抗而言，对组网中的各节点进行方位估计是其中的关键环节。矢量水听器可以同步、共点测量声场空间某点处的声压和质点振速信息，提供更全面的声场信息，同时也可以拓宽信号处理的维度[4-6]。由于振速通道的接收指向性，单个矢量水听器即可实现对目标的无模糊测向，既可以解决在非合作条件下由于先验信息缺失而导致声压阵列阵型设计困难的问题，又降低了接收端对平台的功耗。因此，需要研究利用单矢量水听器对跳频信号的方位估计问题。

文献[7]基于高阶统计的方法利用单矢量水听器对目标方位进行估计，但其需要较高的信噪比条件作为支持；文献[8,9]利用子空间方法，将单矢量水听器的声压振速通道视作多个阵元，进而进行方位估计，但其对矢量水听器通道的相位特性要求较高；文献[10]利用单矢量水听器接收到的数据，构建特殊的状态空间模型，通过对状态过渡矩阵和观测矩阵来获得目标的方位估计，但其目标信号均为单频信号，方法没有考虑频率变化对状态过渡矩阵和观测矩阵的影响；文献[11-13]利用声强法对目标进行测向，但当接收信号为通信信号时，没有利用信号所包含的时频参数信息；文献[14]运用复声强法实现了信号的方位估计，但当信号在频域发生重叠时，会导致重叠频点所对应的方位估计值为两目标的合成方位。复声强法建立了信号频率与方位的关系，但没有利用到信号的时域分布特征，对在时域可分而频域有所重叠的跳频信号的方位估计性能较弱。

本文将信号的时频信息与复声强法结合，将传统复声强法构建的方位与频率的关系扩展到时频域，利用非合作跳频信号的时频特点将原本在频域重叠的信号在时频域分离，进而提升复声强法对跳频信号的方位估计准确性与稳定性。

1 单矢量水听器的信号接收模型

跳频信号是一种频率随时间变化的非平稳信号，可建模为：

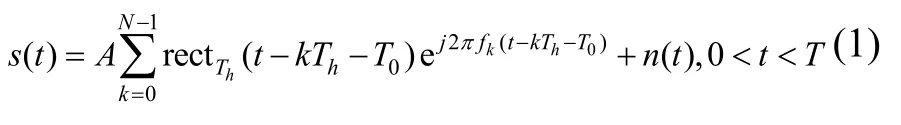
其中，T为观测时间；A为跳频幅度；N为跳频频率数；Th为跳频周期；T0为起跳时刻；为宽度是Th的矩形窗；fk为跳频频率；n(t)为加性白噪声；k为观测时间内，跳频信号的第k个码片。

以两个不同方位入射的跳频信号为例，可对二维矢量水听器（下文所述的矢量水听器均为二维的）接收信号建模为：

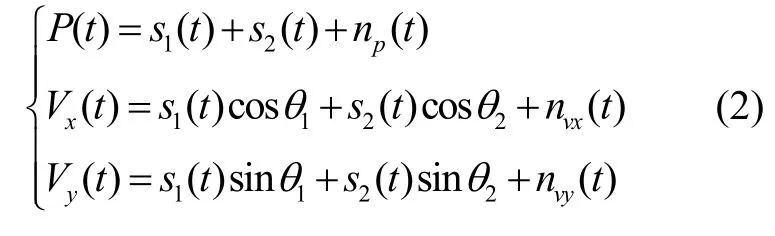
其中，P(t)、V x(t)、V y(t)分别为声压通道以及两个正交振速通道接收到的信号；θ1和θ2分别为两个跳频信号s1(t)和s2(t)的入射角；n p(t)、nvx(t)、nvy(t)分别为声压通道以及两个振速通道接收到的加性白噪声。

2 改进复声强法

2.1 跳频信号时频参数提取

跳频信号属于非平稳信号，时频分析方法是分析这类非平稳信号的有力工具。对于跳频信号，维格纳准概率分布（Wigner Ville Distribution,WVD）方法具有较好的时频聚集性，但存在严重的交叉项问题，导致对信号的时频参数提取产生影响，需要根据跳频信号的特点构建核函数来对交叉项进行抑制进而提高信号时频参数提取的准确性。由于信号的WVD 与模糊函数的二维傅立叶变换等价，而跳频信号的自项在模糊域具有在原点邻域呈哑铃形分布特点，交叉项具有远离原点的特点，因此，可利用矩形窗对信号模糊函数进行处理，进而达到对跳频信号交叉项抑制的效果。

加入核函数后的跳频信号时频分布可通过式(3)表示。

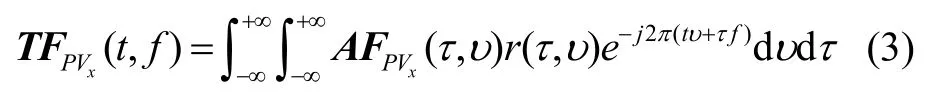
其中，为P(t) 与 ()xV t的互模糊函数，可通过式(4)获得；r(τ,)υ为核函数，可通过式(5)获得。

M 取为模糊平面原点的矩形邻域。在实际应用中矩形区域M 的长和宽可以通过如下方法确定：对原点处时延轴上的模糊分布进行滑动平均，再利用迭代法求得阈值E，记大于阈值的部分的长度为L，即M 的长；跳频信号的交叉项在模糊域的分布相互平行，可沿频率轴搜索，得到距原点最近的极大值，距离记为W，得到M 的宽为W/2。

为了更好地提取信号的时频脊线，需要获得信号清晰的时频图，因此需要对分布于整个时频面上的高斯白噪声进行抑制，可利用迭代去噪法对得到的时频图进行处理。

迭代法的基本思想就是通过寻找合适的阈值ε，来对噪声进行去除，假设信号经过时频变换后得到的时频矩阵为C(t,f)，则：

首先按照式(7)得到初始阈值ε1，再通过式(8)(9)进行阈值更新，直至εk+1=εk时，停止迭代，得到所需要的阈值ε=εk+1。

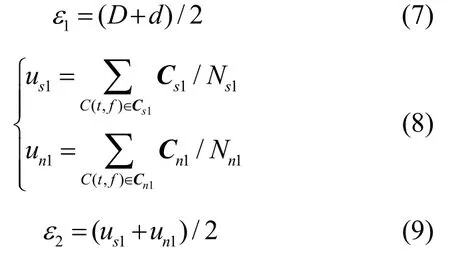
在式(7)(8)(9)中，D为时频矩阵C(t,f)的最大值；d为时频矩阵C(t,f)的最小值；Cs1为C(t,f)中大于ε1的部分；Ns1为Cs1部分中所包含时频点的个数；us1为Cs1部分所有时频点能量的均值；Cn1为C(t,f)中小于ε1部分；Nn1为Cn1部分中所包含时频点的个数；un1为Cn1部分所有时频点能量的均值。

在非合作通信对抗条件下，接收端接收到不同方位的跳频信号具有一定的时延差，如图1 中的信号2与信号3，可利用这一特点，对不同节点的跳频信号从时频域进行分离。对于具有不同跳频保持时间的信号，如图1 中的信号1 与信号2，可通过保持时间的不同对信号进行区分。对于同时到达的且具有相同频率保持时间的信号，如图1 中的信号3 与信号4，可通过对每个跳频序列进行方位粗测，进而通过聚类方式进行区分。

图1 多个跳频信号的时频图Fig.1 Time-frequency diagram of multiple frequency hopping signals

对于跳频信号时频参数提取的处理流程如图2 所示。

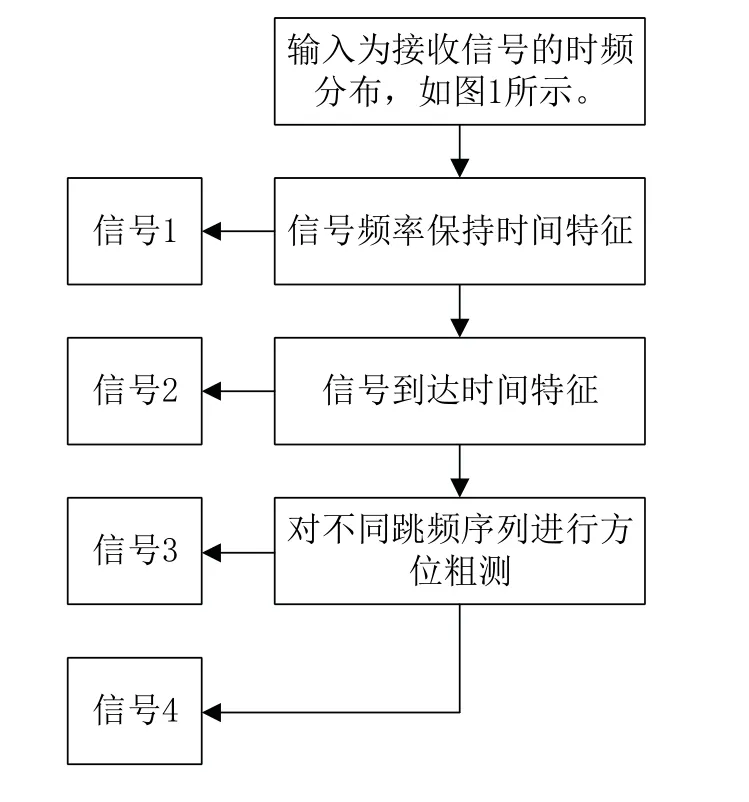
图2 时频参数提取流程图Fig.2 Time-frequency parameter extraction flow chart

首先，通过连通域方法来获得观测时间段内跳频信号每一个跳频序列的时频位置信息，假设观测时间内包含R个跳频序列，每个跳频序列的时频位置信息可表示为(i=1,2,3...,R)，其中，fi为第i个跳频序列的频率；为第i个跳频序列的起始时刻；为第i个跳频序列的终止时刻；ti为第i个跳频序列的保持时间；ti可通过获得。

利用频率保持时间进行信号分离：可通过聚类方法，来对跳频序列的保持时间ti进行聚类，进而将具有不同频率保持时间的跳频序列分离。由于在非合作条件下，在观测时间内跳频信号的个数未知，聚类的簇数无法确定，因此可以利用均值漂移聚类算法对跳频序列的保持时间进行聚类。

利用信号到达时间进行信号分离：对于频率保持时间相同而到达时间不同的跳频信号，可通过比较不同跳频序列中与(i,j=1,2,3...,R)的接近程度进行分离。

利用方位粗测进行信号分离：跳频信号的每个跳频序列具有窄带特性，对不同连通域内的能量进行时间积分，再利用复声强方法进行方法估计，即可获得不同跳频序列所对应的方位信息，进而对得到的每个跳频序列的方位，利用均值漂移聚类方法聚类，从而将具有相同到达时间与频率保持时间的信号分离。

对跳频信号进行区分时，对于发生时频碰撞的码片，矢量水听器无法将其分离，但跳频信号的频率随时间不断跳变，发生时频重叠的部分持续时间较短，因此，可对时频重叠部分的信号从时频域进行剔除，对后续方位估计方法的性能影响较小。

2.2 方位估计方法

利用复声强法测向时，由于信号能量集中于互谱输出的实部，虚部中主要为干扰能量，因此可得到目标水平方位θ的估计值为：

由式(10)可得到声源的方位估计值与其频谱的分布关系，复声强方法对于时频不重叠的窄带信号具有较好的方位估计性能，由于窄带信号在观测时间内的有效时间积分较长，利用互谱法能够有效降低各向同性噪声的影响，进而获得稳定的声强分布。对于跳频信号，其局部为窄带信号，整体为宽带信号，传统复声强方法通常在观测时间内将宽带信号划分为多个窄带信号进行处理，但跳频信号的频率随时间跳变，不同码片对应不同频率，极易出现不同方位信号在频域发生重叠，导致对某些频率的方位估计值为目标的合成方位，产生偏差。同时跳频信号频率集中各频点持续时间较短，利用互谱法无法在观测时间内获得较长的有效时间积分，即使没有发生频谱重叠，对不同频率的声强估计受噪声影响也较为严重，进而影响方位估计性能。

本文方法利用信号的时频特征与复声强方法结合，将传统方法中通过信号频率估计方位的方法扩展为利用信号的时频信息估计方位，相当于变相的增长了复声强方法在观测时间内对信号的有效积分时间，进而提升方位估计性能。方法流程图如图3 所示。

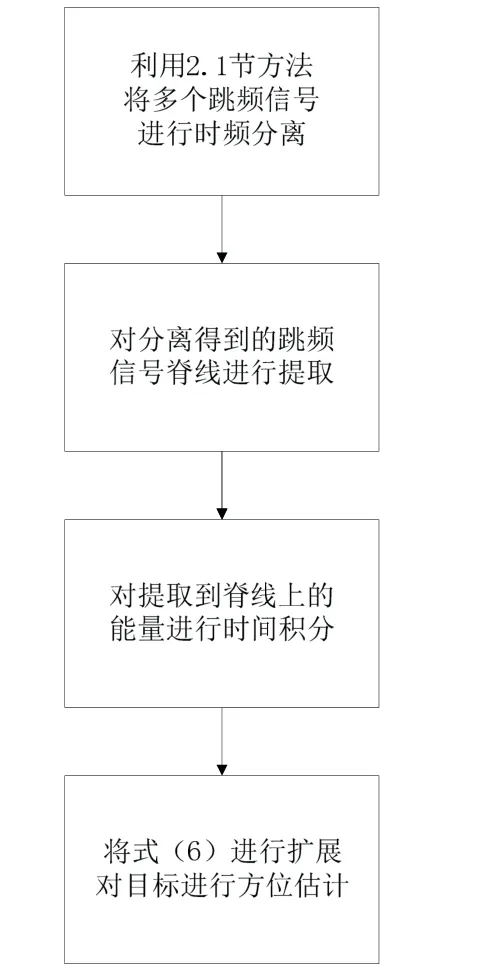
图3 方位估计方法流程图Fig.3 Flow chart of azimuth estimation method

对跳频信号的脊线提取可通过式(11)得到：

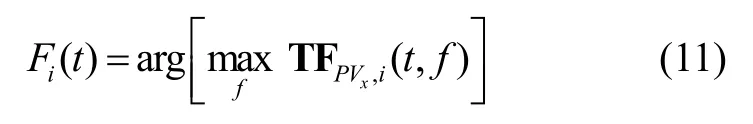
由于跳频信号的能量集中于脊线所对应的时频位置，因此对脊线位置所对应的时频点进行时间积分即相当于增长了复声强法的有效积分时间。可通过式(12)得到改进复声强法的方位估计。

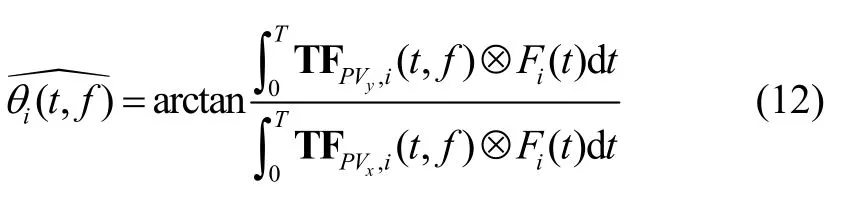
其中，⊗为Hadamard 积。

由于复声强方法建立的是方位与频率之间的关系，且跳频信号每个跳频序列持续时间较短，利用复声强方法得到的方位估计结果受噪声影响较大，本文所提方法联合了跳频信号不同序列之间的时频信息，使观测时间内对信号能量的积分包含了所有跳频序列的时频能量，减小了噪声对方位估计结果的影响，从而提升了复声强方法对目标的方位估计性能。

3 仿真分析与实验测试

3.1 仿真分析

设信号s1的频率集为[2,4,6,8,9,7,5,3] kHz，跳频保持时间为5 ms，入射方位为26.6 °，到达时间为3 ms；s2的频率集为[5,10,3,1] kHz，跳频保持时间为0 ms，入射方位为56.3 °，到达时间为3 ms；s3的频率集为[3,1,5,9] kHz，跳频保持时间为10 ms，入射方位为45 °，到达时间为10 ms；s4的频率集为[7,12,13,4] kHz，跳频保持时间为10 ms，入射方位为123.7 °，到达时间为0 ms。

仿真1：利用短时傅里叶变换（Short-Time Fourier Transform,STFT）、WVD 以及本文方法得到信号的时频分布如图4-6 所示。

图4 STFT 得到的时频分布Fig.4 Time-frequency distribution obtained by STFT

从图4 中可以看出，STFT 方法虽然没有交叉项的影响，但得到的信号时频分布能量不够聚集；图5 中WVD 方法受交叉项影响严重，无法正确提取信号的时频脊线；图6 中为本文方法，加入矩形核函数后，能够很大程度上抑制交叉项的影响，并且具有较好的时频聚集性。

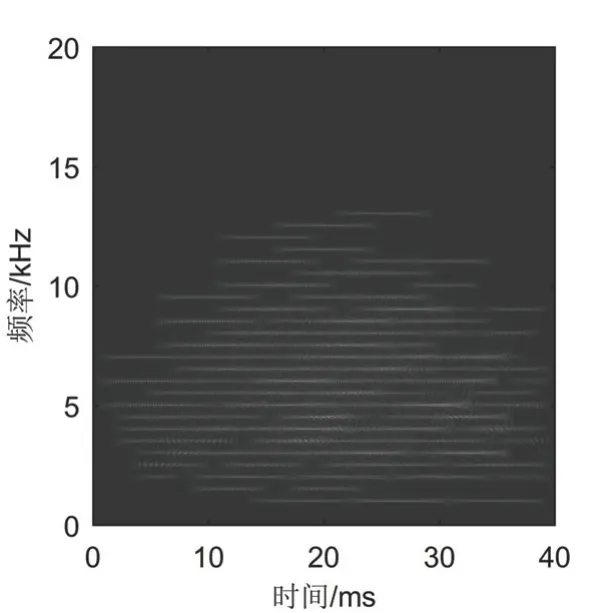
图5 WVD 得到的时频分布Fig.5 Time-frequency distribution obtained by WVD

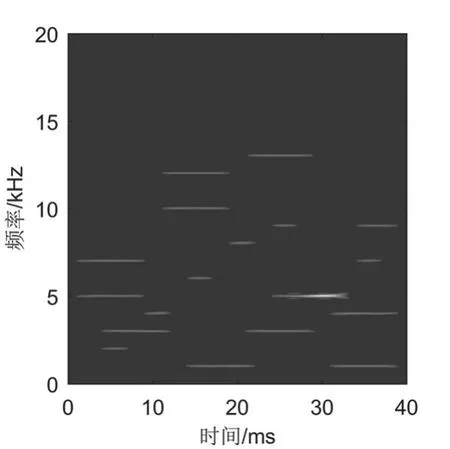
图6 本文方法得到的时频分布Fig.6 Time-frequency distribution obtained by the proposed method

仿真2：利用本文方法对接收信号进行分离，得到结果如图7 所示。

图7 信号分离结果Fig.7 Signal separation result

从图7 中可以看出，本文方法能够有效地对具有不同特征的信号进行时频分离，并对图7(b)与图7(c)中发生时频重叠部分的信号进行剔除。

仿真3：利用本文方法与复声强方法以及加权直方图方法在信噪比为[-3,6] dB 条件下对信号进行方位估计，每个信噪比条件下进行50 次蒙特卡罗实验，得到结果如图8-12 所示。

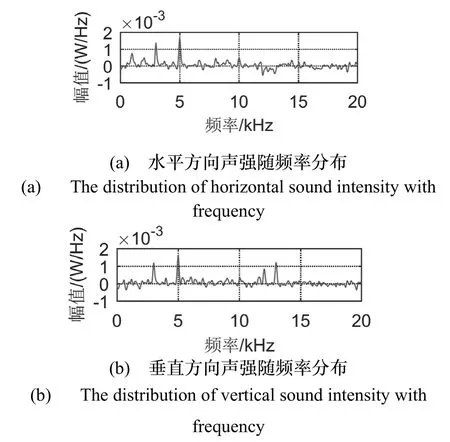
图8 声强分布Fig.8 Sound intensity distribution

从图8 中可以看出，在观测时间内，存在不同方位跳频信号的跳频序列具有相同频率的情况，导致在跳频序列对应的频点处，垂直方向声强值与水平方向声强值之比的反正切值不能正确得到目标的方位信息。同时，由于传统复声强法对信号互谱的时间积分是对于整个观测时间段的，而跳频信号在整个观测时间内，频谱是不断跳变的且每个码片的持续时间较短，导致互谱方法的有效积分时间较短，使噪声对声强估计产生较大影响，进而影响方位估计精度。

从图9 中可以看出，随着信噪比的提高，复声强方法的方位估计精度有所提升，但由于跳频信号局部具有窄带特性，整体具有宽带特性，传统方法通常将观测时间内的宽带信号划分为多个窄带信号，进而利用复声强法对多个窄带信号进行方位估计，当观测时间内的不同方位信号在频域出现重叠时，由于没有结合信号的时域信息，无法将频域重叠的信号有效剔除，导致复声强法即使在信噪比较高的情况下也对目标方位估计具有一定误差。

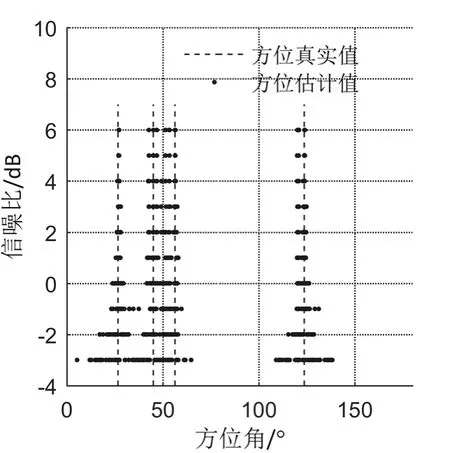
图9 复声强法在不同信噪比下的方位估计结果Fig.9 Azimuth estimation results of complex acoustic intensity method under different SNR

图10 为利用加权直方图方法对目标的方位估计结果。加权直方图方法是一种通过对方位间隔内的声强累计，进而得到目标方位估计的一种统计方法。相较于复声强方法，其具有较好方位估计性能。但其需要利用复声强法对所有频率分量进行方位估计，对于在频域重叠的跳频序列的方位估计仍存在一定误差。

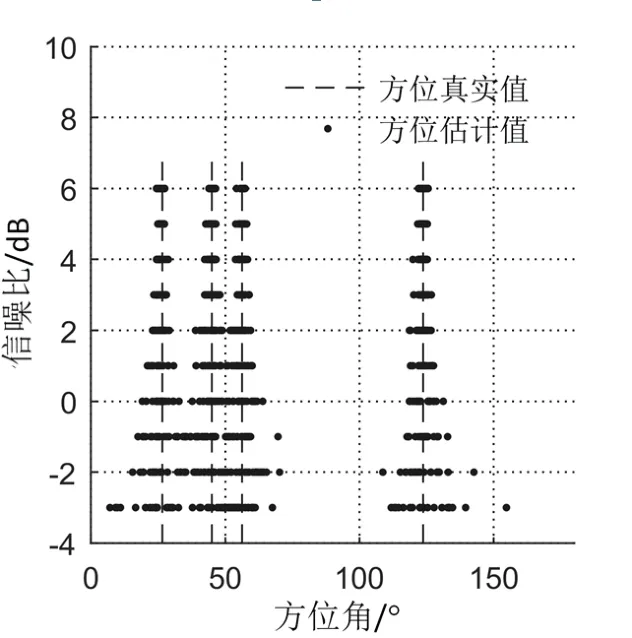
图10 加权直方图法在不同信噪比下的方位估计结果Fig.10 Azimuth estimation results of weighted histogram method under different SNR

本文方法扩展了复声强法的维度，利用了信号的时频特征，对具有相同时频特征的信号在时频域进行能量积分，相当于提升了传统复声强方法的有效积分时间，进而获得更好的方位估计精度。对比图9、图10 与图11，可直观地看出，本文方法相比于传统复声强方法与加权直方图方法，在不同信噪比条件下均具有较好的方位估计效果。

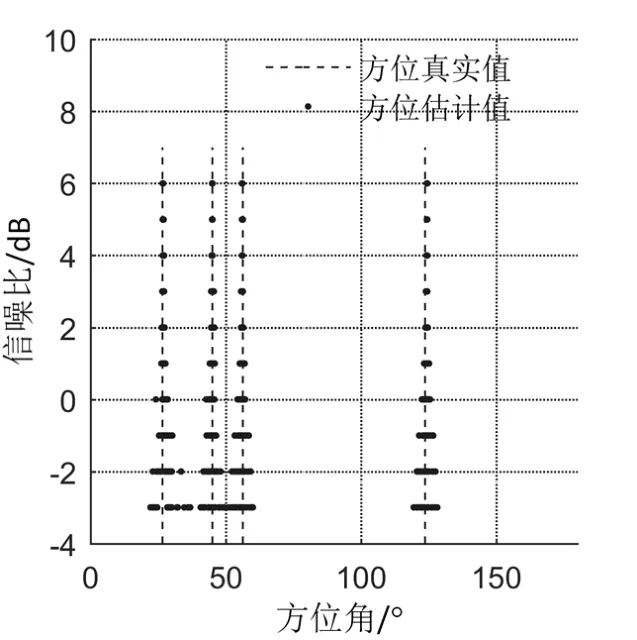
图11 本文方法在不同信噪比下的方位估计结果Fig.11 Azimuth estimation results of the proposed method under different SNR

从图12 中可以看出，随着信噪比的提升，方法性能有较大提升，原因是在信噪比较高的情况下，能够获得信号清晰的时频图，对信号脊线的提取更加稳定，进而能够明显提升本文方法的方位估计精度。

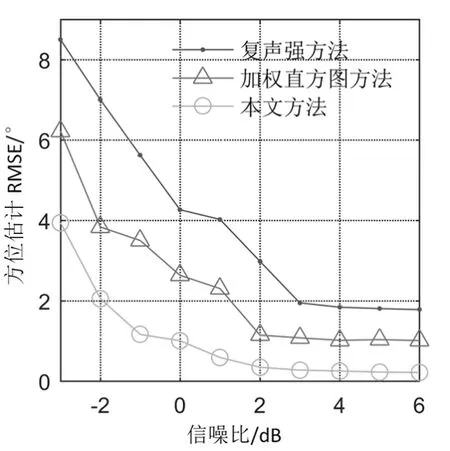
图12 不同信噪比下的方位误差均方根误差Fig.12 Root mean square error of azimuth estimation at different SNR

3.2 水池实验测试

实验测试是在长宽深为(25 m×15 m×10 m)的消声水池中进行。实验硬件系统主要包括发射与接收两部分。发射部分主要包括控制模块、信号源、功率放大器以及发射换能器，利用控制模块，通过设置信号源的触发方式来控制发射信号的时延。接收部分主要包括矢量水听器、前置放大滤波系统、以及多分析仪系统B&K PULSE 3560D 构成，信号采样频率设置为60 kHz，搭建的实验接收系统如图13 所示。

图13 接收系统Fig.13 Receiving system

实验发射信号参数与仿真信号参数相同，信号循环发射，信号源设置峰峰值为25 mV，水池中发射换能器(声源1，声源2，声源3，声源4)与接收系统(矢量水听器)位置关系如图14 所示，矢量水听器及声源均布放于水下5 m 处。

图14 水池实验布置示意图Fig.14 Schematic diagram of pool experimental arrangement

取长度为1 s 的数据进行处理，设置观测时间为50 ms，即将数据分为20 段，利用本文方法与复声强方法得到的方位历程图如图15 所示。

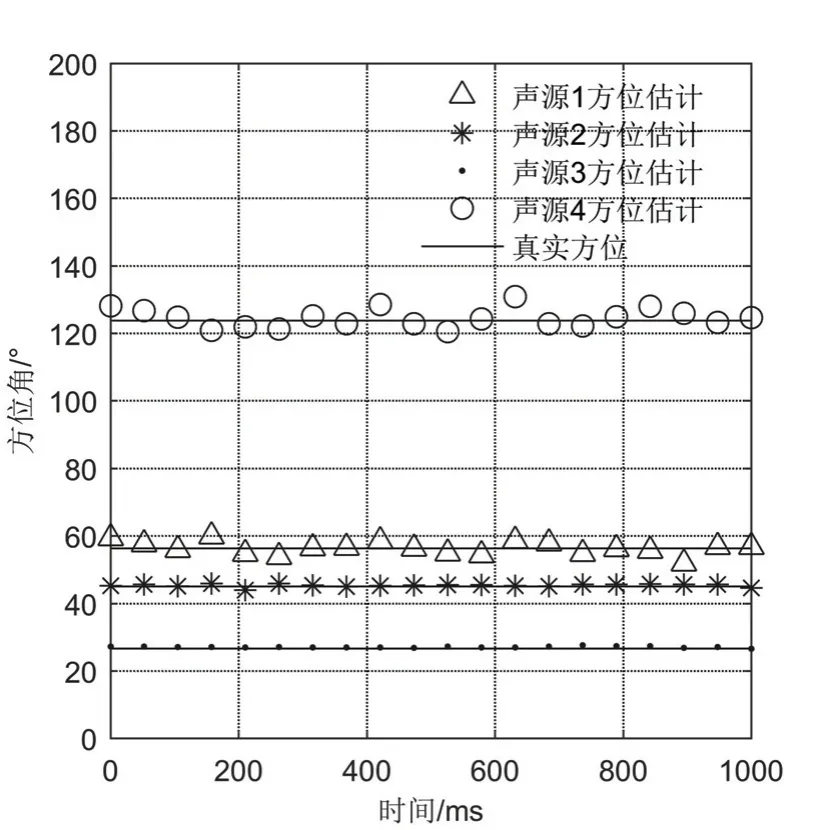
图15 目标方位历程图Fig.15 Target azimuth history map

从图15 中可以看出，本文方法对于不同方位入射的多个跳频信号均具有较好的方位估计结果。其中对声源2 与声源3 的方位估计相较于对声源1 与声源4效果更好，是由于4 个声源所用信号源发射信号的峰峰值相同，而声源2 与声源3 距离接收端较近，具有更高的接收信噪比。利用本文方法对目标方位估计值的均方根误差为0.7 °。实验结果表明，本方法将信号的时频特征与复声强方法结合后，能够明显提升对方位估计的精度与稳定性。

4 结论

针对传统方法对非合作跳频信号方位估计性能不佳的问题，本文通过理论分析，将复声强法中方位与频率的关系扩展到时频域，利用跳频信号模糊分布的特点，通过构建核函数来对二次型时频分布的交叉项进行抑制，再通过跳频信号时频分布的特点，对跳频信号的时频脊线进行提取，提升了传统方法对跳频信号方位估计的稳定性；通过对时频脊线对应的能量整体进行时间积分，能够提升传统方法的有效积分时间，解决了跳频信号码片对应频率持续时间较短导致传统方法方位估计精度较低的问题，并通过水池实验验证了所提出方法的有效性。本文方法在信噪比大于0 dB时，方位估计均方根误差小于1°，为水声对抗平台对跳频信号的方位估计提供了一种有效方法，同时也可作为定位导航、目标跟踪等领域的一种辅助方法。