全球/区域地形和重力异常间相干性分析

范 雕，李姗姗，赵东明，杨军军，孟书宇，范昊鹏

（1.信息工程大学，郑州 450001；2.中国自然资源航空物探遥感中心，北京 100083；3.32022 部队，广州 510630）

海洋观测是研究海洋、开发海洋和利用海洋的基本手段，是加强海洋国防建设、预警海洋灾害、开发海洋资源、发展海洋经济、谋求新发展空间等的重要支撑。海底地形作为海洋观测的重要组成内容，其探测技术历来是各海洋国家相关组织机构的研究热点。目前海底地形测量技术主要包括船基海底地形测量技术[1]、潜基海底地形测量技术[2]、机载激光雷达测深（Airborne Lidar bathymetry，ALB）技术[3]、星基海底地形测量技术[4,5]等。船基海底地形测量技术测量（使用单波束、多波束设备测量）精度高，但就全球海域而言，存在测量效率低下且测量结果分布极不均匀等缺点。ALB 技术测量效率高，主要用于测量海区水质较好的浅海环境，应对深海海域或者严重影响光束传播海域地形测绘能力有限。星基海底地形测量技术中基于卫星测高技术构建海底地形是目前主要依赖的快速构建全球海底地形方法手段，可有效满足海底地形全球性、连续性、智能化和动态化观测要求。

卫星测高技术构建海底地形基本原理是利用覆盖海面的卫星测高重力数据，采用相应的重力反演海底地形方法间接恢复海域海底地形数据[6-9]。海面重力异常主要受海水质量亏损、地壳密度分布不均匀、地壳以下质量的均衡补偿等因素影响[10]，从而利用卫星测高重力数据仅可恢复有限频段海底地形信息[11]。据此可知，确定重力反演海底地形有效截止频段范围是依据卫星测高技术构建海底地形的方法前提[12,13]。基于此，本文一方面以EGM2008、EIGEN-6C4 全球重力场位系数模型和DTM2006、EARTH2012 全球地形球谐系数模型为数据输入，使用全球地形-重力相干性处理方法，解算了全球范围内地形和重力异常频谱相干性特征，给出了全球范围地形-重力表现强相干性的频段参考范围；另一方面，以实际海域局部海底地形和海面重力异常为真实数据参考，使用区域地形-重力相干性计算方法，获取了真实海域地形-重力表现强相干性的频段参考。研究结果以期为利用卫星测高重力数据恢复海底地形信息截止频段的确定提供参考与借鉴。

1 理论与方法

相干性（Coherency）也称为幅值平方相干（Magnitude Squared Coherence,MSC），表征输入信号在频域空间的线性相关程度。假设时域输入信号分别为x(t) 和y(t)，那么信号频域相干性可表示为信号互功率谱密度（Cross-Power Spectral Density，cross-PSD）的正常化结果：

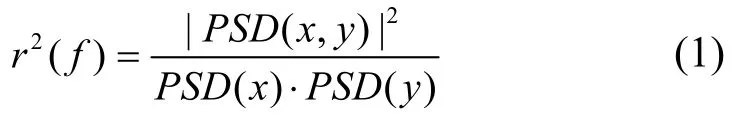
式中，r2(f)表示相干性；PSD(x,y)表示信号x(t)和y(t)的互功率谱密度；PSD(x)和PSD(y)分别表示信号x(t) 和y(t) 的自功率谱密度（Auto-Power Spectral Density,auto-PSD）。

1.1 球地形与重力场元间相干性

由重力场知识可知，重力异常可表示为：

式中，PSD表示功率谱密度；其余参数意义同上。

利用地形球谐系数模型求解地形h（高度起算面为平均海平面）公式如下[15,16]：

利用式(2)和式(4)可得地形和重力异常的互功率谱密度：

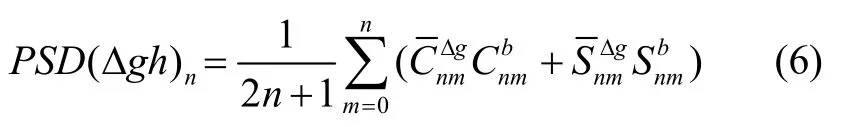
式中参数意义同上。

依据相干性分析可得重力异常和地形的相干性为：

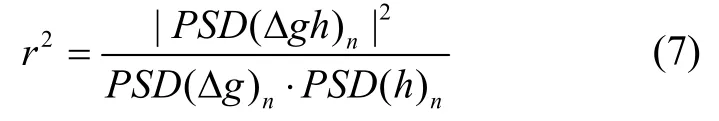
依据文献[10]可知空间分辨率（ψ为两点的地心角距）与模型阶数（n）的关系为：

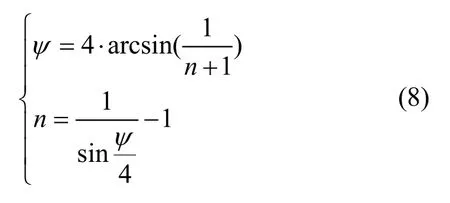
1.2 区域地形与重力场元间相干性

设海面某类重力场元符号为Γ（重力异常、重力异常垂直梯度等），海底地形为b，则依据导纳函数可得重力场元Γ 与海底地形b的频率域表达式为[17]：

式中，F(Γ)和F(b)分别表示重力场元Γ 与海底地形b的傅里叶变换；ZΓ为重力场元Γ 对应的导纳函数，如当Γ 表示重力异常，考虑挠曲均衡补偿时，导纳函数ZΓ函数形式为：

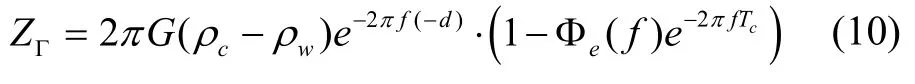
式中，G为地球引力常数；ρc和ρw分别表示地壳密度和海水密度；d为海域平均海深（取负）；Φe(f)为挠曲响应函数；Tc为地壳厚度；f表示径向频率。同理，当不考虑均衡补偿、考虑Airy 均衡补偿以及顾及多层地壳结构时，导纳函数ZΓ均存在类似的表达形式，具体参见文献[18]。对式(9)中导纳函数施以傅里叶逆变换操作，同时依据卷积定理可得：

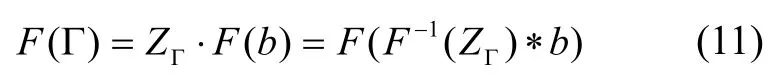
式中，F-1() 表示傅里叶逆变换；“*”表示卷积运算。从而重力场元Γ 可表示为：

式(12)为依据海底地形恢复海面重力场信息的表达式。实际测量中，重力场元Γ 将不可避免存在噪声影响，设噪声与重力场元Γ 和海底地形b相互独立，从而式(12)可表示为：

式中，ω表示测量噪声。依据Wiener-Khintchine 定理和相关定理，重力场元Γ 的自功率谱密度可表示为：

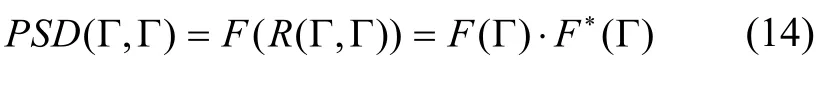
式中，R(Γ,Γ) 表示重力场元Γ 的自相关函数；F*(x)表示F(x) 的共轭。将式(13)带入式(14)，据傅里叶变换线性性质、共轭性质、时域卷积定理、相关定理和Wiener-Khintchine 定理，同时顾及噪声与重力场元和海底地形相互独立条件可得：

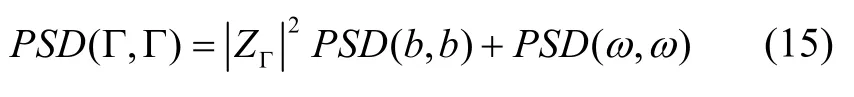
同理可得，海底地形的自功率谱密度为：

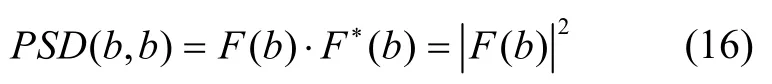
重力场元与海底地形互功率谱密度为：

从而，根据信号间相干性关系可得重力场元和海底地形相干性为：

令重力场元信号和测量噪声的信噪比表达式为：

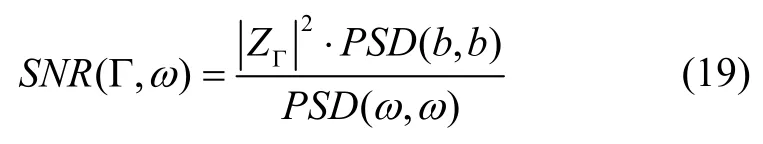
从而依据式(18)可知，1）相干性等于0.5 可以理解为：海底地形信号b不含噪声的情况下，重力场元Γ 的信噪比为1：1；2）当重力场元信号Γ 和海底地形信号b均不含噪声情况下，二者的频域相干性恒为1。也就是说，当重力场元信号与海底地形信号相干性在0～1之间时，原因可能有：

（1）重力场元噪声影响。若重力场元与海底地形服从线性关系，理论上二者频域相干性数值大小应为1，然而由于重力场元信号存在噪声导致二者频域线性相干性不为1；如图1 显示了重力场元在不同信噪比环境下信号间相干性变化情况。通过图1 可以看出，随着重力场元信号信噪比不断增大，相干性也随着不断增大；即噪声的影响导致重力场元与海底地形线性相关程度降低。

图1 相干性随信噪比变化曲线Fig.1 Coherency curve with SNR

（2）重力场元信号Γ 与海底地形信号b实际线性相关程度较低。①重力场元信号和海底地形信号相干性表示二者的线性相关程度，实际上基于Parker 公式[19]推导的重力导纳函数仅仅是Parker 公式的线性近似，忽略了高次项海底地形对海面重力场元影响，二者实际并非完全线性相关，从而相干性不等于1；②海面重力场元并非完全受海底地形影响，海底洋壳的均衡状态、海底地形的密度差异以及海水结构等因素均会不同程度地改变海面重力场元信息，从而海面重力场元与海底地形相干性表现为0～1 间变化。

重力场元信号和海底地形信号均为功率有限信号时，依据Wiener-Khintchine 定理和相关定理，信号间相干性可表示为：

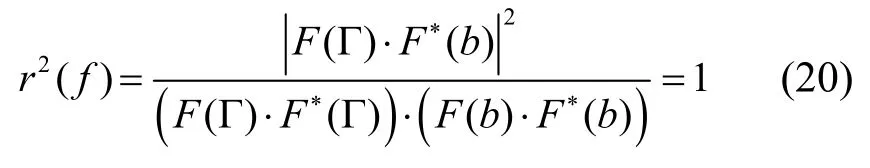
根据式(20)可知，若输入信号为功率有限信号，则按照式(20)计算信号间相干性，不论信号是否相关以及线性相关强弱，二者频率域相干性恒为1。针对这一问题，通常应对策略为将式(20)解算的功率谱密度进行平滑处理：式中，<>表示方位角α范围内的平均值。方位角的取平均值实际操作流程如下[20-22]：

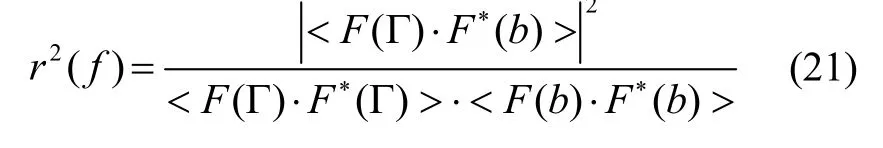
（1）坐标转换。将频率笛卡尔坐标系（fx、fy）转换为极坐标系（f，α），两坐标系间坐标关系为：

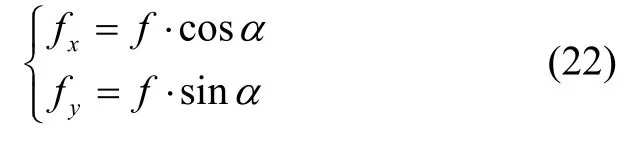
式中，fx和fy分别表示x和y方向上的频率；其余参数意义同上。

（2）方位角范围取平均。径向频率取值范围为[0 min（f x,fy）]，以dq为径向频率间隔，分别计算环径为dq范围内的各信号功率谱密度平均值，然后依照式(16)解算信号相干性。

2 数值分析试验

2.1 算例1：全球地形和重力场元相干性

当前国际广泛使用的超高阶（大于1000 阶）重力场模型有EGM2008、GECO和EIGEN系列等模型等。本文以EGM2008（2160 阶）和EIGEN-6C4（2190 阶）地球重力场模型作为计算重力异常谱的重力场输入，以EARTH2012（2160 阶）和DTM2006（2190 阶）地形球谐系数模型作为解算地形谱的数据输入，依据式(3)和式(5)计算的重力异常功率谱密度和地形功率谱密度结果如图2 和图3 所示，其中红色曲线分别表示EGM2008 和EARTH2012 位系数模型计算结果，蓝色曲线分别表示EIGEN-6C4 和DTM2006 位系数模型解算结果。可以看出，重力异常和地形的功率谱密度均随着模型阶数的增加而减小，说明模型中长波信号占主要部分，高频信号能量较弱；而EIGEN-6C4 模型功率谱密度在2160 阶后出现急剧变化，这与模型构建机制有关，如使用的数据分辨率等因素。根据式(6)计算EGM2008 和EARTH2012 之间的互功率谱密度如图4 中红色曲线所示，EIGEN-6C4 和DTM2006 之间的互功率谱密度曲线如图4 中蓝色曲线所示。利用式(1)获取的分别以EGM2008 和EARTH2012 模型为输入，以及以EIGEN-6C4 和DTM2006 模型为输入的相干性结果如图5 中红色和蓝色曲线所示。

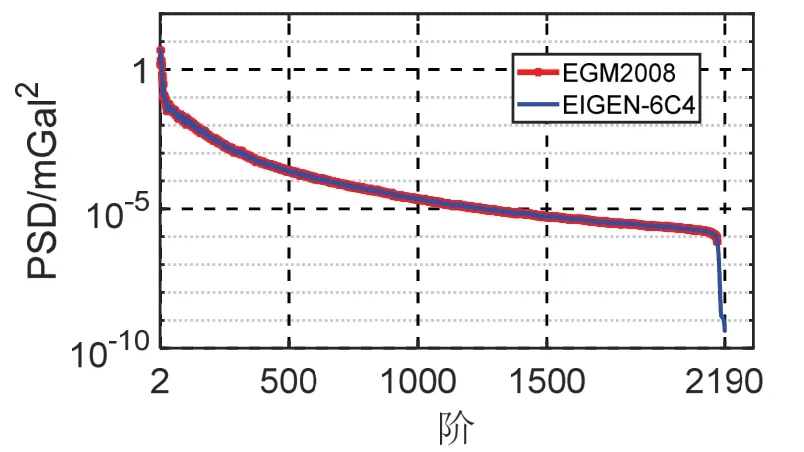
图2 重力异常自功率谱密度Fig.2 The auto-PSD of gravity anomaly

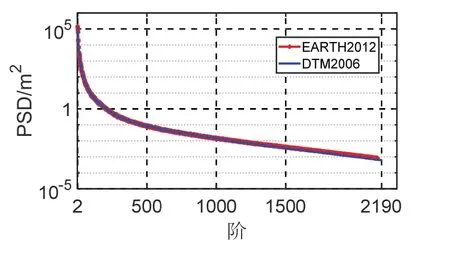
图3 地形自功率谱密度Fig.3 The auto-PSD of topography

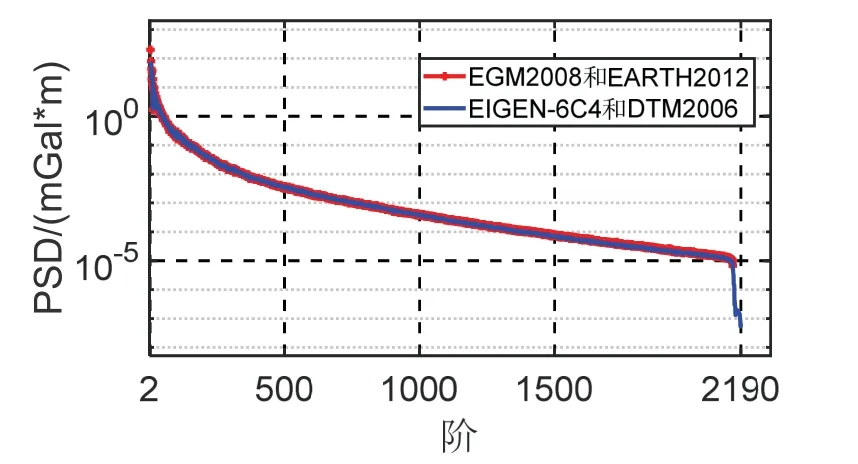
图4 重力异常和地形互功率谱密度Fig.4 The cross-PSD of gravity anomaly and topography

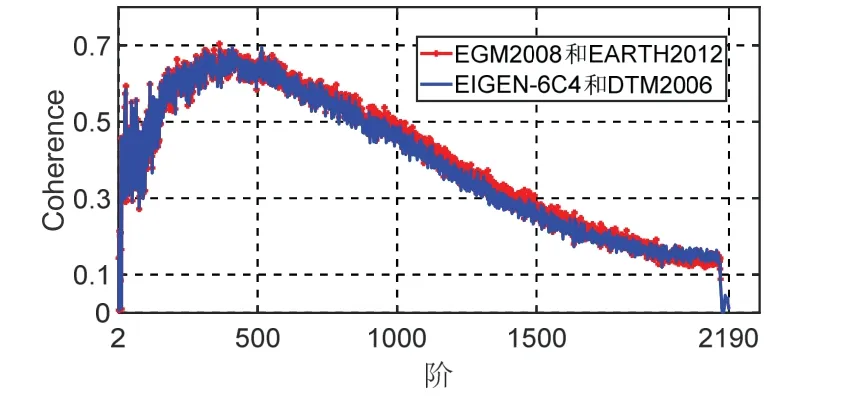
图5 重力异常和地形相干性Fig.5 coherence between gravity and topography

图5 重力异常和地形的相干性结果表明，随着阶次的增加，二者相干性呈现先升高后降低的特征。由相干性定义可知，相干性表示一种信号可线性转换成另一种信号的程度：当相干性为1 时即两种信号完全线性相关；相干性为0 表示两信号没有线性关系[23]。当相干性为0.5 可理解为信噪比（signal-to-noise，SNR）为1:1 的信号与另一不含噪声信号的相干性结果[24]。从图5 可以看出，全球范围内重力异常和地形的相干性在0.5 以上对应的模型阶数大约为120阶～1000阶，对应的波长范围为25.45 km～210.61 km，该计算结果与目前国际国内学者利用重力数据恢复海底地形的波段范围一致[6,7,17,25-28]。

2.2 算例2：区域地形和重力场元相干性

选择某3 °× 3°（12°N～15° N，112 °E～115°E）海域作为研究海区，遵照以上理论分析研究海区海底地形和重力异常频域相干性大小。研究海区水深数据（格网化水深）和卫星测高重力异常数据（S&SV24.1）空间分辨率为1 角分，空间分布情况如图6 所示。相应数据统计结果见表1，数据类别括号内为数据单位。

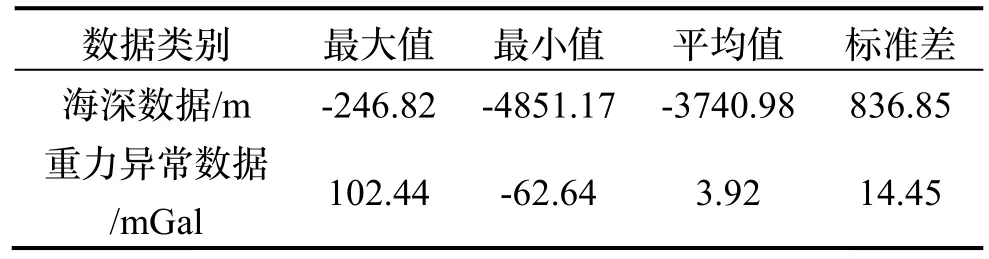
表1 研究区域数据概况Tab.1 Information about data in the study area

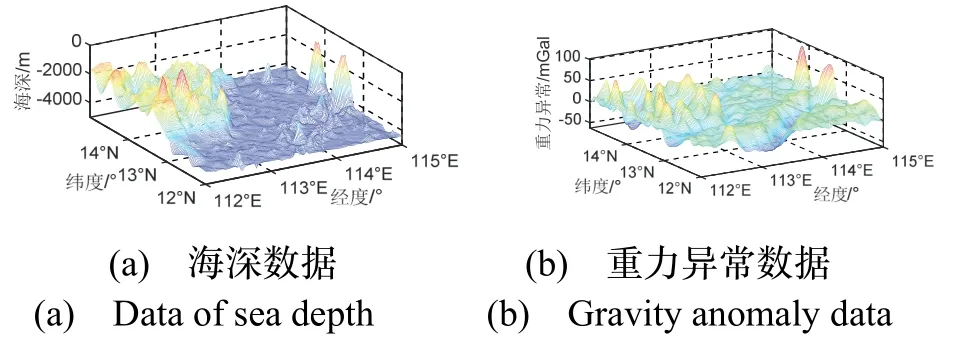
图6 研究区域数据Fig.6 Data in the study area

经计算，研究区域东西向总长为324.37 km，南北向总长为333.58 km，其中南北沿纬度方向由于变形在距离计算时施加了部分改正，而东西沿经度方向可近似认为不发生形变（不加改正），从而东西向和南北向长度不相等。依据研究区域边长可得沿纬度方向和经度方向频率间隔为0.003/km 和0.0031/km。选择纬度方向频率间隔和经度方向频率间隔平方根作为径向频率间隔（0.0043/km）,最大径向频率为0.2698/km，依据相干性计算流程，最终得到研究海区海底地形和重力异常相干性结果如图7。从图7 相干性结果可以看出，海底地形和重力异常在有限波段表现出较强的相干性。需要说明的是，由于实际数据更加复杂，包含的信息量更多，噪声模式不尽相同，从而不同区域地形和重力异常相干性结果也不尽相同。

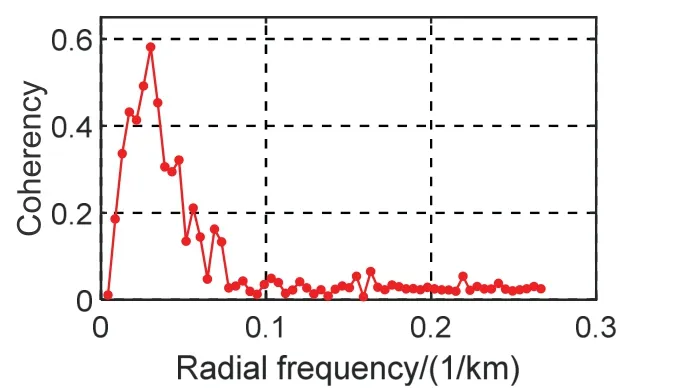
图7 海底地形和重力异常相干性结果Fig.7 The result about coherency between seafloor topography and gravity anomaly

3 结论

本文一方面以EGM2008、EIGEN-6C4 全球重力场位系数模型和DTM2006、EARTH2012 全球地形球谐系数模型为数据输入，研究了全球范围地形自功率谱、重力异常自功率谱和地形-重力互功率谱特点，计算分析了全球范围地形-重力异常相干性频谱特点。另一方面，使用某3°×3°（12°N～15°N，112 °E～115°E）海域作为真实研究海区，充分研讨了局部区域海底地形-重力异常间相干性特点，分析了重力场元信噪比、非线性项海底地形和地壳均衡等影响干扰局部地形-重力相干性结果情况。通过实例计算得出：全球范围地形-重力异常在120 阶～1000 阶左右表现强相干性，对应波段范围是25.45 km～210.61 km。研究结果可为利用卫星测高重力数据恢复海底地形信息截止频段的确定提供参考与借鉴。