基于深度学习与运动状态识别的车辆惯性导航方法

黄凤荣，羿博珩，王 旭，刘庆璘，王文森

（1.河北工业大学 机械工程学院，天津 300401；2.中国人民解放军93756 部队，天津 300131）

微机电系统（Micro-Electro-Mechanical System,MEMS）惯性测量单元（Inertial Measurement Unit,IMU）因成本低、尺寸小以及功耗低等优势在各个领域有广泛应用需求[1]；但MEMS IMU 误差大且复杂，具有非线性、时变性等特点，在惯性导航的双积分过程中传感器误差会以指数方式传播，导致采用MEMS IMU 的车辆导航系统误差随时间迅速增大，无法满足导航定位需求；针对此问题，惯性导航领域一般采用标定补偿的方法对传感器误差进行处理，传统的基于线性模型的惯性元件误差标定方法分为分立式标定和系统级标定，但对于MEMS IMU 巨大且复杂的误差，传统标定方法已经明显不适用。再者，考虑车辆导航定位可以利用车辆运动中的特殊运动信息，如在不打滑、不腾空的情况下，车辆横向和垂向的速度为零，那么，利用这些约束信息进行信息融合可以在一定程度上抑制车辆导航定位的误差。

随着深度学习的发展，数据驱动方法已开始被引入惯性导航领域，Chen H 等人[2]描述了一种基于深度学习的消除IMU 误差的方法，该方法可在实验室环境下消除MEMS IMU 信号中的许多误差源，与传统的六位置静态测试和速率测试方法进行了比较，结果表明，该方法对IMU 信号的正确识别率达到80%。Jiang C 等人[3]提出了一种对MEMS IMU 输出信号进行去噪的人工智能（Artificial Intelligence,AI）方法，将信号处理为时间序列，并使用长短期记忆（Long Short-Term Memory,LSTM）对MEMS 陀螺仪的输出信号进行滤波。Esfahani M A 等人[4]根据IMU 的不同测量类型，提出了一种三通道LSTM 网络架构，使用两个连续IMU 读数之间的时间间隔作为惯性网络的另一个输入，以回归三维相对位移和旋转的幅度，但无法从这些输出预测三维位置。Brossard M 等人[5]使用卷积神经网络（Convolutional Neural Networks,CNN）动态估计车辆运动简单模型的不确定性，并结合不变扩展卡尔曼滤波（Invariant Extended Kalman Filter,IEKF）来估计车辆的位置、速度。

总之，基于深度学习技术标定IMU 误差，以及进行运动状态检测开始引起研究者的关注，目前在此方面的研究刚刚起步，公开的研究成果还很稀少。但已有的研究表明，基于深度学习进行MEMS IMU 误差标定补偿和运动状态检测相结合无疑是一种新思路。本文针对车辆导航问题，提出一种基于深度学习与运动约束的车辆导航方法，该方法在有效补偿IMU 陀螺仪误差的基础上，又对车辆运动状态进行了准确估计，最后，利用不变扩展卡尔曼滤波进行信息融合实现车辆导航。

1 车辆导航算法

1.1 算法框架

首先，基于改进后的膨胀卷积网络（Dilated Convolutional Networks,DCN）[6]对MEMS IMU 陀螺仪误差进行标定补偿。其次，利用时间卷积神经网络（Temporal Convolutional Networks,TCN）[7]动态检测车辆的运动状态。同时，将特定的运动状态信息作为观测量，基于不变扩展卡尔曼滤波进行信息融合，从而提高车辆导航系统的定位精度，算法框架如图1 所示。

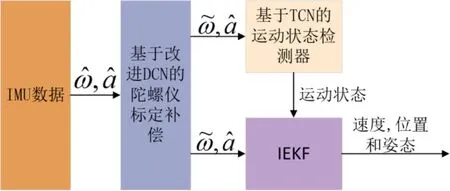
图1 算法框架Fig.1 Overall algorithm framework

1.2 基于改进DCN 的陀螺仪误差标定补偿方法

传统陀螺仪标定补偿方法[8-11]没有考虑IMU 误差模型非线性的特点，为了表征MEMS IMU 误差的非线性，本文提出了一种基于改进DCN 的陀螺仪标定补偿方法。该方法使用改进DCN 构建MEMS 陀螺仪的误差输出模型，网络模型以MEMS IMU 的测量数据作为输入，输出误差补偿后的陀螺仪数据。

1.2.1 惯性元件输出模型

MEMS IMU 的输出受多种误差源的影响，比如安装误差、刻度因子误差、零偏和随机漂移等，惯性元件的输出模型可以表示为：

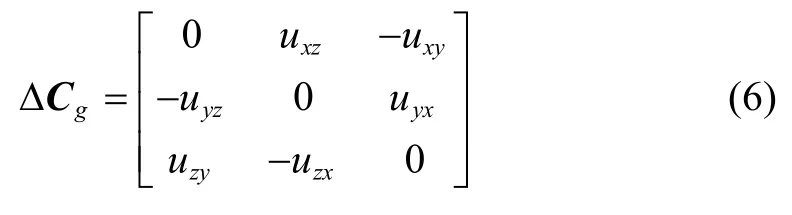
其中，Sα、Sg为加速度计和陀螺仪的刻度因子误差矩阵，ΔCα、ΔCg为加速度计和陀螺仪的安装误差矩阵，是IMU 轴系与载体系之间存在安装误差导致的。bα、bg是加速度计和陀螺仪的零偏，ε、η是随机漂移，通常看作是零均值高斯白噪声。

目前，MEMS IMU 误差主要来源于陀螺仪，陀螺仪的误差对导航结果影响更大，因此，本文对MEMS IMU 陀螺仪漂移进行标定补偿。通过对MEMS IMU陀螺仪输出的误差分析，经过误差补偿的陀螺仪输出可以表示为：

其中，A=(I+Sg+ΔCg)-1包含刻度因子误差参数和安装误差参数，为标定补偿后的陀螺仪输出，陀螺仪的零偏具有随机性和时变性，因此误差B可看作是一种时变误差。估计出矩阵A和时变误差B并补偿即可减小MEMS 陀螺仪的测量误差。

改进DCN 利用过去N个时刻的IMU 数据来预测误差B，可以表示为：

其中，f(∙)是改进DCN 逼近的非线性函数，IMUt是MEMS IMU 在t时刻的输出值，IMUt-N是在MEMS IMU 在t-N时刻的输出值。

1.2.2 网络结构

为使网络模型更符合MEMS 陀螺仪的误差特性，在采用深度神经网络对MEMS 陀螺仪的输出建模时，我们将整个网络模型分为两部分，一部分是DCN，其输入为加速度计数据和陀螺仪数据，负责预测式(8)中的误差B，另一部分是一层跨连接1D 卷积层，输入只有陀螺仪数据，负责预测矩阵A，流程如图2 所示。

图2 标定流程图Fig.2 Calibration flow chart

为准确估计包含刻度系数误差和安装误差参数的矩阵A，本文使用了一个3 输入通道3 输出通道的跨连接层，其跨越了整个DCN。该跨连接层是一层1D卷积层，跨连接层的输入为MEMS 陀螺仪测量值，输出为，这一层的输出可以看作是对MEMS 陀螺仪测量数据的微调，是补偿部分误差后的陀螺仪数据。

1.2.3 损失函数

改进DCN 是一种监督学习方法，需要真实值作为监督信息来评估网络模型的好坏，在公开数据集中，含有使用高精度导航系统得到的精确姿态信息，本文以精确的四元数作为神经网络的监督信息，本文的损失函数如下：

其中，式(9)中n是一个控制损失大小的参数，进而也能控制网络训练过程中梯度的大小，它的取值是通过多次试验确定的，Q为四元数真实值，是根据计算得到的四元数。需要注意的是，在计算损失之前，四元数Q、都是经过归一化的。为了防止过拟合现象，损失函数并不输出每一时刻四元数的损失，而是累积x个点的损失后输出一次损失，这里x的大小为8。

1.3 基于时间卷积神经网络的运动状态检测

在本节将介绍车辆运动的典型状态，这些运动状态被正确检测后会作为观测量，为基于IEKF 进行信息融合做准备。

1.3.1 运动状态检测

考虑3 种不同的运动状态，并用二进制向量来表示运动状态的有效性：

• 零速状态：车辆的速度为零。

横向速度和垂直速度需要在车身系下表示：

• 侧向零速状态：横向速度近似为零。

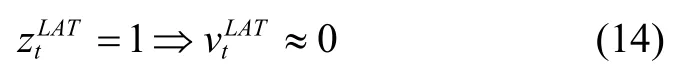
• 垂直零速状态：垂直速度近似为零。

运动状态检测器在每个时刻t确定哪些特定运动状态是有效的，其中由TCN 组成的运动状态检测器从标定补偿陀螺仪误差后的IMU 信号估计每个运动状态的概率分数，基于概率分数通过阈值判断输出二进制向量，即运动状态。检测器结构如图3 所示，我们将为0 的概率分数的阈值设置为0.9，将和的阈值设置为0.5。

图3 运动状态检测器结构Fig.3 Structure of motion state detector

1.3.2 网络结构

时间卷积神经网络（TCN）是一种应用于解决时间序列建模问题的网络结构，它具有梯度稳定和占用计算资源少等特点。每个运动状态对应一个TCN，每个TCN 由4 个残差块组成，每个残差块包含两个膨胀因果卷积层（卷积核大小设置为5），归一化方面，残差块使用了权重归一化[12]；使用GELU 函数[13]来提取特征；使用Dropout[14]进行正则化以避免过拟合，具体的网络参数如表1 所示。

表1 时间卷积神经网络的参数设置Tab.1 Parameter setting of time convolution neural network

1.3.3 损失函数

因为要对3 个不同的运动状态进行判断，我们需要解决三个二元分类的问题，所以我们使用多标签损失函数（BCE With Log its Loss）：

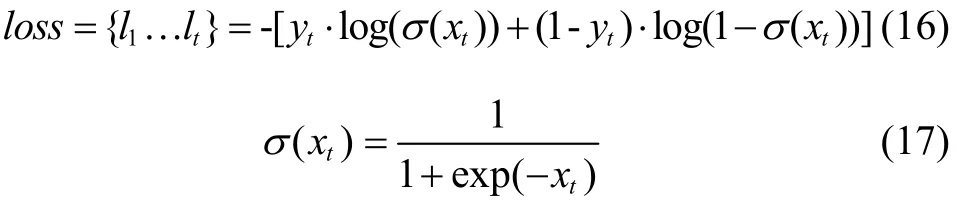
其中，lt为每个类别的损失，xt为模型输出，yt为标签值，σ(xt)为Sigmoid 函数，可以把xt映射到(0,1)的区间。

1.4 基于IEKF 的信息融合

传统扩展卡尔曼滤波（EKF）[15]的系统矩阵依赖当前状态估计值，在有噪声引入时，系统对状态估计值的预测是不准确的。当状态估计值与真值差距较大时，直接导致系统矩阵也有较大偏差，若使用这样的系统矩阵继续计算，将进一步放大误差，使系统形成正反馈，最终导致滤波器发散。此外，EKF 还存在不一致性问题，即EKF 的更新步骤是通过旧状态的线性化来计算当前状态的协方差矩阵，但是其与当前状态协方差矩阵的实际值并不一致。

为解决上述问题，不变扩展卡尔曼滤波（IEKF）基于李代数，将群变换应用于系统状态变量，所以IEKF 的状态量是一个矩阵，并且构成群[16]。为了实现系统矩阵与状态估计值的独立，解决传统EKF 存在的问题，将误差也定义在群上。因此，我们将标定补偿陀螺仪误差后的IMU 测量值集成到其动态模型中，并将检测到的运动状态的约束信息作为观测量，基于IEKF 进行信息融合来完善其估计值。

车辆的动力学模型如下：

其中，Rt表示将载体坐标系映射到导航坐标系的旋转矩阵，vt表示速度，pt表示位置，[ ]×表示3 × 3斜对称矩阵，g为重力加速度，dt为解算步长，ωt是标定补偿后的陀螺仪输出，a t是加速度值。在应用场景中，我们假设车身框架与IMU 框架对齐，并且忽略地球自转和科里奥利加速度的影响。

我们将系统状态定义为：

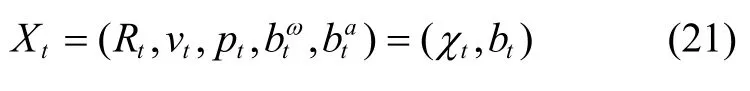
其中，χt∊SE2(3)为矩阵李群，由方向余弦矩阵Rt、速度vt、位置pt和IMU 误差构成。

增广右不变误差定义为：

其中，ηt为右不变误差，ζt为普通线性误差。

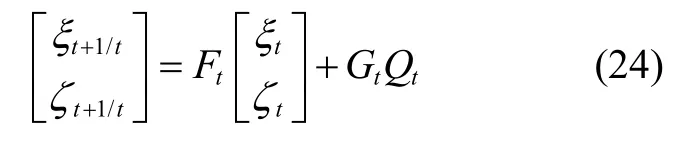
其中，ξt为ηt对应的李代数，并映射到状态，Ft为系统矩阵，G t和Qt分别为系统噪声分配矩阵和系统噪声向量。

IEKF 算法流程如下：

1）初始化X0，P0；

2）时间更新：如果未检测到特定运动状态，我们应用式(18)-(20)得到状态Xt+1，通过黎卡提微分方程得到协方差Pt/t1-，协方差公式如下：

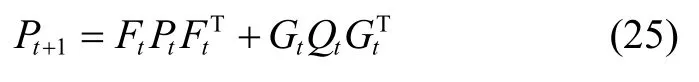
3）量测更新：每个运动状态产生以下量测值之一：

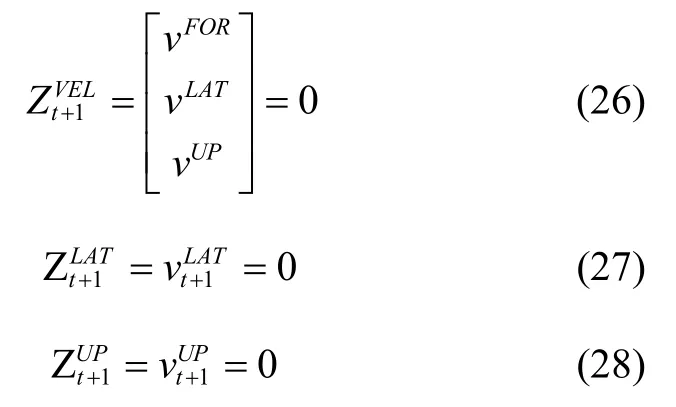
需要特别注意的是，当检测到零速状态时，我们不考虑侧向零速状态和垂直零速状态，因为零速已将其包括在内，如果未检测到特定运动，则跳过测量更新步骤。

计算增益矩阵Kt，更新Xt以及更新协方差Pt

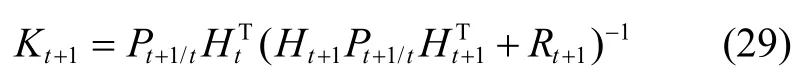
更新后的线性化状态误差为：

其中H为：

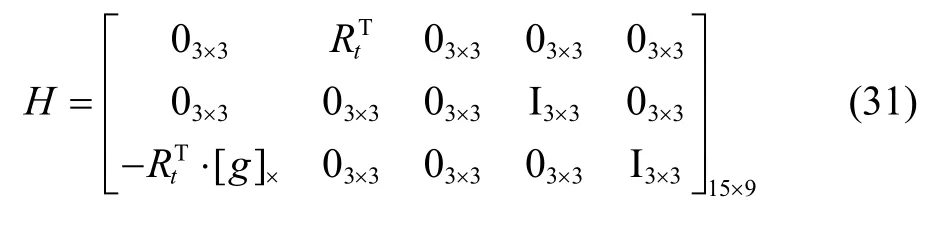
可得状态更新公式：

2 实验描述

为了验证本文提出的基于深度学习与运动约束的车辆导航方法的有效性，本文采用公开 KAIST URBAN 汽车数据集进行了实验验证。实验将数据集分为训练集和测试集，在训练集上标定陀螺仪误差参数和优化神经网络，训练结束后在测试集上回归误差补偿后的陀螺仪数据，运动状态检测同理，并进行导航解算，数据集分配如表2 所示。同时，与其他两种基于深度学习的方法进行了比较，并定义了评估标准。

表2 KAIST URBAN 数据集训练集和测试集分配Tab.2 KAIST URBAN data set Training set and test set allocation

2.1 数据来源与训练细节

KAIST URBAN 数据集提供车辆在复杂环境下(大都市地区、复杂建筑和居住区)收集到的数据，其中包含多种传感器数据，比如激光雷达、FOG、GPS和AHRS IMU 等，同样给出了真实姿态、位置信息。在这个数据集中，地面真值是通过位姿图SLAM 生成的。整个数据集中的IMU 数据是使用Xsens 的MTi-300 获得的，采样频率为100 Hz。

关于网络训练，本文的网络是使用Pytorch 实现的，并在RTX 2060 GPU 上进行实验。网络的训练分为陀螺漂移标定补偿和运动状态检测两部分，均使用ADAM[17]优化器完成网络训练。

其中，陀螺标定补偿网络训练初始学习率为0.001，并且自适应地调整学习率，当损失变化很小时调整学习率，训练回合为1000。为了防止网络过拟合，权重衰减参数设为0.1，Dropout 层的参数设置为0.2，除此之外，在网络训练时，本文还对训练集进行了数据增强处理，提高数据的多样性，增强模型的鲁棒性。

使用ADAM 优化器在200 个周期内对运动状态检测器进行训练，初始学习率为0.0001 并由学习率程序自适应调整，训练回合为500。对于每个时期，我们将数据分为一批2 分钟的序列，随机设置每个序列的初始时刻，但每个序列的开始时刻都有至少1 秒的静止状态，以保证滤波器能够良好地初始化。

2.2 评估标准

为了评估性能，我们考虑了两个误差指标：

1）绝对轨迹误差（Absolute Trajectory Error,ATE,m）：

绝对轨迹误差描述的是位置估计值ˆp与位置真实值P之间的相似度，以均方根误差来计算。

2）相对轨迹误差（Relative Trajectory Error,RTE,m）：

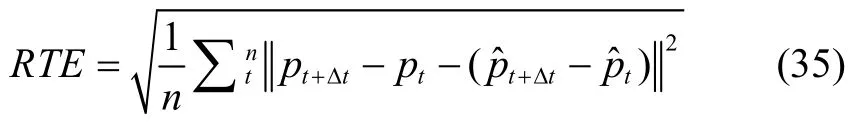
相对轨迹误差描述的是在一个时间为Δt的窗口内，位置估计值增量与位置真实值增量之间的相似度，这里的Δt为1 s。

2.3 实验结果

在Urban11 到Urban16 序列上训练完后，我们在测试序列Urban6 到Urban10 上进行评估，本文比较了三种方法。

1）基于TCN 检测的零速信息融合方法：未对陀螺仪误差进行标定补偿，IMU 测量值直接进入IEKF，仅考虑零速状态，若检测到零速状态，则将零速状态约束信息作为观测量，基于IEKF 进行信息融合。

2）基于TCN 检测的特定运动状态约束融合方法：未对陀螺仪误差进行标定补偿，IMU 测量值直接进入IEKF，将零速状态、侧向零速状态和垂直零速状态作为特定状态，若特定状态被检测到，则将特定的运动状态约束信息作为观测量，基于IEKF 进行信息融合。3）本文方法：标定补偿陀螺仪误差后的IMU 测量值进入IEKF，将零速状态、侧向零速状态和垂直零速状态作为特定状态，若特定状态被检测到，则将特定的运动状态约束信息作为观测量，基于IEKF 进行信息融合。

为了对位置精度进行评估，本文计算了整个测试集水平位置和三维位置的ATE/RTE 的平均值，如表3所示。

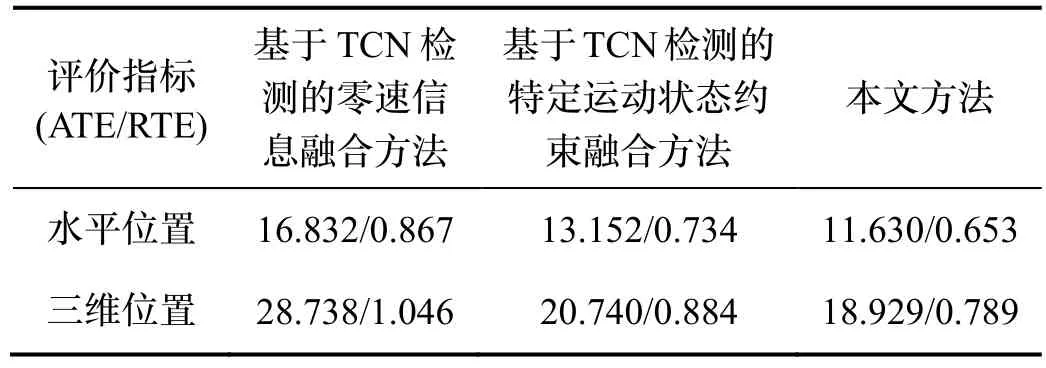
表3 不同方法在整个测试集水平位置和三维位置的ATE/RTE 平均值对比Tab.3 Mean ATE/RTE values of different methods at horizontal and 3D positions were compared

利用本文方法解算的导航结果位置精度有了明显提升，相比其他两种方法在水平位置ATE/RTE 平均值分别缩小 30.9%/24.7%，11.6%/11.0%；三维位置ATE/RTE 平均值分别缩小34.1%/24.6%，8.7%/10.7%。

各个测试序列的ATE/RTE 值，如表4 所示，从数值可以直观地看出，本文的方法得到的位置信息更加可靠，这说明所提出的方法能够有效提高车辆导航定位精度。

表4 不同方法在各测试序列三维位置的ATE/RTE 对比Tab.4 ATE/RTE values of different methods at 3D positions of each test sequence were compared

图4 是在测试序列Urban07 上三维位置轨迹估计图，相比另外两种方法，本文方法得到的位置误差值更小。

图4 Urban07 序列三维位置轨迹对比图Fig.4 Urban07 Sequence 3D position trajectory comparison

经过计算，相比基于TCN 零速检测方法，利用本文方法测试Urban07 序列最终的水平轨迹误差从22 m减小到12 m，而且高度误差大幅降低，约小于4 m，Urban07 测试序列水平位置轨迹估计图，如图5 所示。

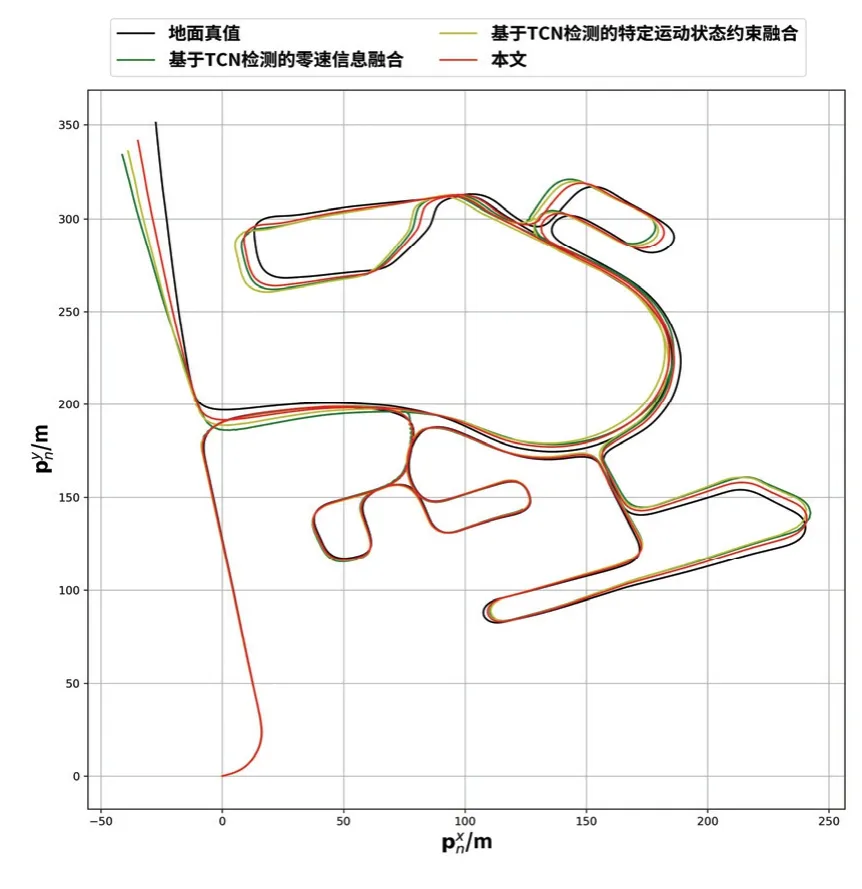
图5 Urban07 序列水平位置轨迹对比图Fig.5 Urban07 Sequence horizontal position trajectory comparison

3 结论

由于MEMS IMU 误差大且复杂，具有非线性、时变性等特点，由此基于MEMS IMU 的捷联惯性导航系统误差在短时间内快速发散，其精度远远不能满足车辆导航需求，本文提出了一种基于深度学习与运动约束的车辆导航方法。该方法先使用改进后的膨胀卷积网络构建了一种具有非线性、时序性、多因素耦合等特点的陀螺仪输出模型，利用过去时刻的IMU 数据预测当前时刻陀螺仪输出的误差，并对其进行补偿。其次，利用时间卷积神经网络动态检测车辆的运动状态，同时，将特定的运动状态约束信息作为观测量，基于IEKF 进行信息融合。本文在公开数据集上验证了所提出的方法，并与基于TCN 检测的零速信息融合方法和基于TCN 检测的特定运动状态约束融合方法进行了对比，实验结果表明该方法能够有效提高位置精度，降低位置误差。

本文已经证明深度神经网络在车辆导航定位中有着良好的应用前景，但是深度神经网络有着庞大数量的参数，在实际应用中需要具有强大运算能力的嵌入式处理器，计算过程会消耗一定的时间，其计算的实时性也是影响实用性的一个重要因素。进一步优化算法，提高算法的实用性是未来的工作。