面向城市复杂环境的GNSS/INS 高精度图优化算法

韩勇强，于潇颖，纪泽源，陈家斌

（1.北京理工大学 自动化学院，北京 100081；2.北京理工大学 光电学院，北京 100081）

惯性/卫星组合导航由于其高精度、高鲁棒性等诸多优点，成为地面、空中等多类移动平台广泛采用的重要导航模式。但城市复杂环境下，卫星信号易被建筑物遮挡且受多路径和非视距等效应影响[1]，导致GNSS 信号出现粗差或者信号丢失情况。

近年来，图优化算法(Factor Graph Optimization,FGO)相比扩展卡尔曼滤波算法(Extended Kalman Filter,EKF)在数据融合方面体现出了明显优势[2]。IMU 预积分对图优化算法的精度具有重要影响，现有图优化算法应用背景多采用低精度IMU，往往忽略惯导解算中的地球自转与有害加速度积分项。为了提高预积分精度，文献[3,4]提出了考虑地球自转的IMU 预积分模型。文献[5]验证了即使对于消费级MEMS-IMU，现有的IMU 预积分也不够精确，必须改进；并将改进的预积分模型应用到GNSS/INS 组合导航系统中，构建了基于优化的GNSS/INS 集成导航系统 (Optimization-Based GNSS/INS Integrated Navigation System,OB-GINS)，该系统显著提高了基于FGO 的GNSS/INS 积分的精度，但OB-GINS 系统并没有考虑卫星信号在复杂环境下的局限性。

当卫星信号出现短暂粗差时，图优化算法无法感知传感器性能变化，认为异常的观测值依旧在可控范围内，进而导致估计误差增大；EKF 算法对异常的观测值具备一定的判别能力，可降低粗差对系统估计造成的影响，但当卫星信号恢复正常时，无法及时作出响应，进而影响系统后续的估计精度。总而言之，无论是滤波算法还是优化算法，卫星粗差观测值一旦作用到系统，都会导致严重估计误差。针对上述问题，国内外的研究学者开展了大量研究。文献[6]提出了一种基于残差卡方检验方法容错卡尔曼滤波器方案，包括三个子滤波器和一个主滤波器。文献[7]设计了一种冗余量测噪声协方差估计方法，可有效剔除多路径等影响产生的野值。文献[8]基于模糊理论的隶属度函数，提出了一种模糊强跟踪EKF 算法，可以快速适应卫星信号突变。文献[9]使用卡尔曼滤波新息值，设计了一种基于高斯检验的鲁棒估计方法。文献[10]结合惯导与卫星原始信息进行导航系统故障检测，而后基于故障检测结果对故障因子节点进行自适应隔离。本文针对高精度IMU/GNSS 数据融合问题，重点解决预积分模型不准与卫星定位粗差抑制问题，提高组合导航系统的位姿解算精度。

针对城市复杂环境下高精度、高鲁棒性导航定位的需求，本文在构建IMU 因子、GNSS 因子的基础上，搭建了基于因子图的惯性/GNSS 数据融合算法架构(GNSS-Inertial navigation system with Gross error Detection,GD-GINS)，通过改进预积分模型，提升了因子图优化算法精度；基于卫星信息关联性的特性，设计了一种在线滑动窗口粗差检测算法，可有效提升卫星观测粗差影响条件下的组合导航精度。最后通过仿真和试验验证本算法的优越性。

1 多源融合图优化理论

因子图是由变量和因子节点组合而成的双边图模型，通过对状态随时间的后验概率进行编码，来解决不同频率异构传感器融合问题，如图1 所示。

图1 基于图优化的GNSS/INS 融合框架Fig.1 GNSS/INS fusion framework base on factor garph optimization

在GNSS/INS 融合导航系统中，第k时刻的状态误差变量节点的最小化误差函数为：

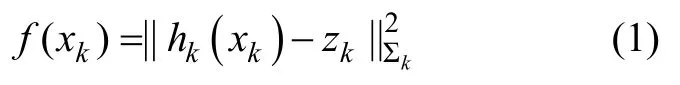
两个相邻时刻变量节点之间的约束定义为二元状态转移因子：

基于图优化的组合导航算法，最小化所有测量残差的先验和马氏距离之和，以获得最大后验概率估计。

2 基于GNSS/INS 的高精度图优化算法

2.1 算法方案

如图2 所示，本文提出的图优化算法主要分为卫星、惯导和非线性优化三个模块。卫星数据进入卫星模块做预处理，惯导数据进入惯导模块做预处理，预处理后的数据插入到非线性优化模块的滑动窗口内；在非线性优化模块中，新的传感器数据加入到滑动窗口后，进行局部状态优化，如果滑动窗口内的状态数量达到阈值，则进行边缘化处理。

图2 算法方案Fig.2 Algorithm diagram

2.2 坐标系与待优化状态定义

如图1 所示，导航系统中的待优化状态变量定义为X=[x0,x1…xn]。其中xk为：

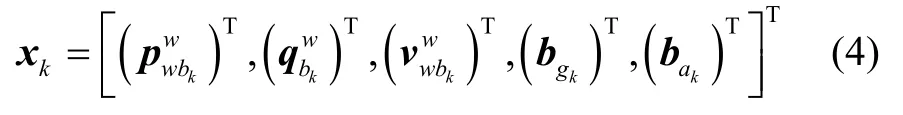
其中，b系为载体坐标系，x、y、z轴分别指向载体前、右、下方，且与载体固连。w系为导航坐标系，x轴指向正北，y轴指向正东，z轴指向地。为tk时刻载体在w系下的位置向量、姿态四元数和速度向量，和分别为陀螺仪和加速度计的零偏。

2.3 卫星惯导模块

(1) 卫星滑动窗口粗差检测

GNSS 观测信号在多帧之间是相关的，基于该特性，本文构建滑动窗口，根据窗口内数据的统计概率值检测新的测量值是否为粗差。

计算窗口内测量值的均值和标准差：

其中，l=1,2…L，L是观测序列的维数。

如果m+1 时刻测量值被剔除，使用窗口内历史观测值拟合出新的观测值代替粗差。本文假设导航系统前100 s 内卫星信号处于开阔视野中，通过前100 s 内观测值的统计概率特性确定λ的取值。

(2) 构建GNSS 因子

GNSS 位置和速度因子的残差函数分别为：

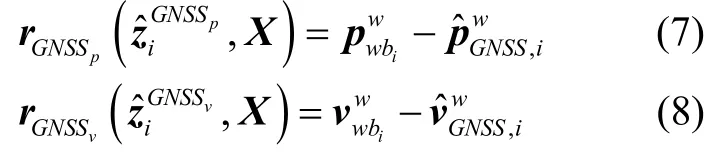
(3) 惯导模块

IMU 测量模型：

其中，e系为地心地固坐标系，i系为惯性坐标系。本文参考文献[7]中的IMU 预积分模型，该模型相比于传统的IMU 预积分模型，考虑了地球自转加速度，进而引入科氏加速度以提高模型精度。载体运动引起w系相对于e系的转动角速度在w系内的投影，记为，由于其引起的误差小于本文使用的传感器误差，所以本文忽略了该项。

IMU 预积分因子的残差函数定义为：

2.4 非线性优化模块

(1) 滑动窗口优化

基于图优化的组合导航算法，最小化所有测量残差的先验和马氏距离之和，以获得最大后验概率估计。

根据上述推导得到的矢量形式的表达式：

令A=JTΣ-1J，B=

为使上式的值最小，即使其一阶导数为0，可得：

则状态变量的解为：

最后使用LM 迭代法求解最优值，获得增量ΔX。

(2) 状态边缘化

当窗口内的状态数量超出阈值时，将最旧的状态边缘化，并将边缘化状态对应的IMU 预积分测量和GNSS 位置和速度测量转化为先验因子。

根据最优化理论，采用LM 线性优化方法对残差进行优化时，每次迭代等价于求解增量方程

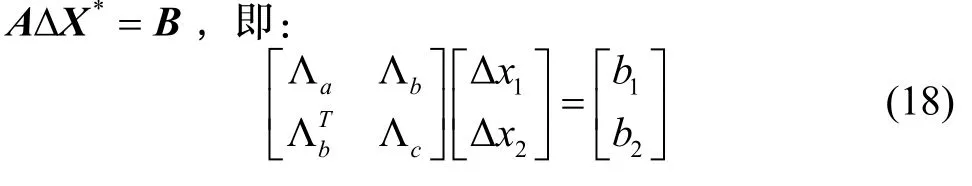
两边同乘舒尔项：

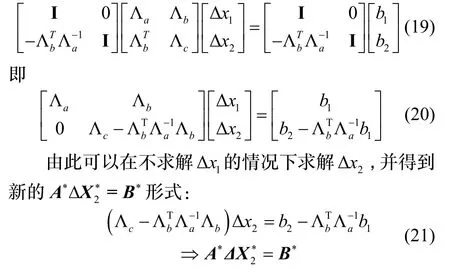
通过舒尔补过程，将要消去的变量Δx1构建的约束关系叠加到和其有观测关系的变量Δx2上，保留了先验信息。

3 GNSS/INS 图优化算法实现

综上，本文算法流程如图3 所示。首先判断GNSS信号是否拒止，如若拒止，则等待下一时间节点；如没有拒止，则将该时刻观测值插入粗差检测滑动窗口进行处理，经过粗差检测后，将GNSS 数据从全局坐标转换为局部坐标，构建GNSS 位置因子、GNSS 速度因子，同时通过初始的位置得到重力加速度、地球自转角速度参数；利用INS 数据构建IMU 预积分因子。将构建的各传感器因子插入到因子图中进行局部状态图优化，得到优化状态值。

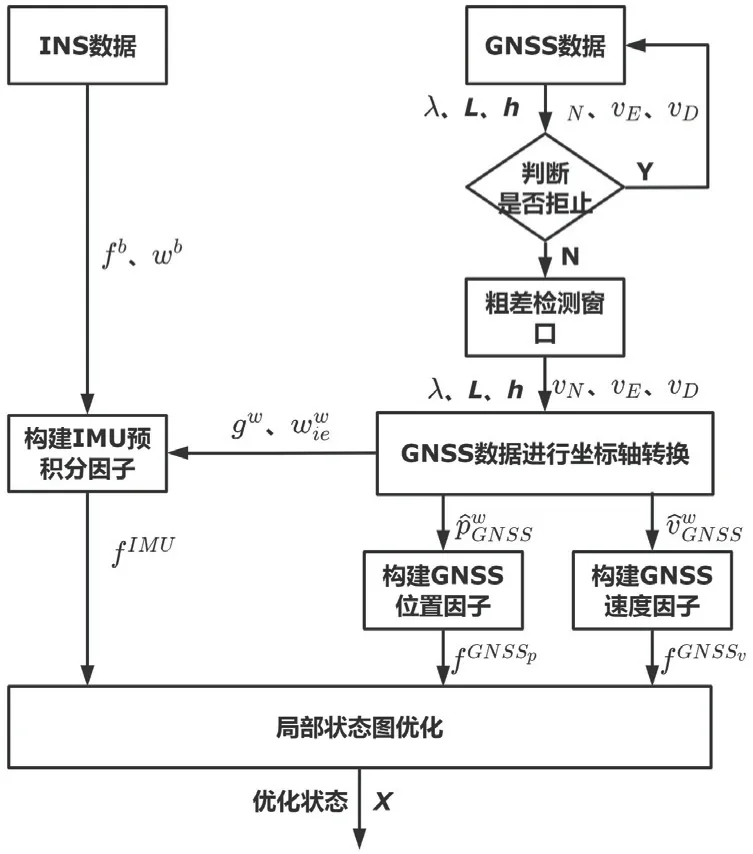
图3 基于图优化的GNSS/INS 组合导航流程图Fig.3 Flowchart of GNSS/INS integrated navigation based on factor graph optimization

4 试验验证

4.1 仿真试验

本文基于MATLAB 平台生成了一条仿真路线，路线方案如图4 所示，其中包括加速、减速、拐弯、上坡、下坡等各种运动情景。各传感器的更新频率、零偏及观测误差如表1 所示。

图4 仿真轨迹Fig.4 Simulation trajectory

表1 传感器更新频率及误差Tab.1 Update frequencies and errors of the sensors

基于该仿真轨迹，本文通过将本文提出方法和EKF、OB-GINS 对比，从而对提出方法的实时状态估计的性能进行评估。图优化与EKF 之间存在以下不同，第一，图优化算法使用多次迭代来最小化成本，而EKF 对每个状态只进行一次迭代；第二，与EKF执行的单一线性化不同，图优化在每个状态的每个迭代步骤都对非线性测量模型进行线性化；第三，由于图优化的批处理性质，所以其能够更好地利用过去和现在时期之间的时间相关性，特别是，在批处理模式下，图优化相当于每次测量更新后的前向滤波器和后向平滑器[11,12]。OB-GINS 是将惯导数据、卫星接收机的位置信息作为观测量通过图优化算法进行融合，其也采用了改进的IMU 预积分模型，GD-GINS 相比OB-GINS 来说，增加了卫星接收机的速度信息作为观测量，并且具备卫星粗差处理机制。

如图5(a)所示，在位置估计方面，GD-GINS 与OB-GINS 算法的估计效果几乎一致；在速度和姿态估计方面，由于GD-GINS 加入了GPS 速度信息，所以相较于OB-GINS 精度有明显提升，如图5(b)(c)所示。此外，GD-GINS 相比于EKF 来说，在位置、速度和姿态状态量估计上均有小幅改善。

图5 各方法导航误差对比图Fig.5 Comparison chart of navigation error of each method

4.2 实车数据仿真试验

为了进一步评估所提出方法的鲁棒性和精度，利用在城市道路采集的真实导航数据集，本文开展了仿真试验。试验车辆装有IMU、GPS 信号接收仪和高精度激光陀螺惯导/GNSS/里程计组合导航系统（作为轨迹基准）。各传感器的更新频率、零偏及观测误差如表1 所示。

试验全程总时长987 s，跑车测试轨迹如图6所示。100～210 s 间纬度出现了峰值为600 m 的突变连续性粗差信号，200～400 s 间经度出现了峰值为400 m 突变连续型粗差信号，持续时间在5 s 以内；700～800 s 间出现卫星拒止情况。

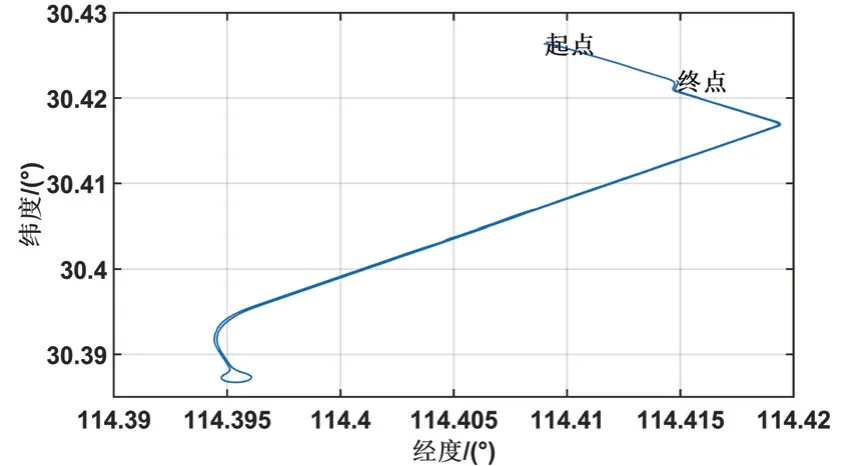
图6 跑车测试轨迹Fig.6 Test trajectory of the car

图7 为实时状态估计的效果图，在100-400 s 之间卫星定位出现了粗差，在700-800 s 之间卫星信号拒止。在100-400 s 之间，GD-GINS 的粗差检测机制可有效降低卫星粗差带来的干扰。700-800 s 之间卫星拒止时，三种算法均只有纯惯导解算，因三者惯导解算方式不同，所以三者误差积累有所不同。EKF 为捷联导航算法，虽GD-GINS 和OB-GINS 同为预积分方式，但初始状态不同。

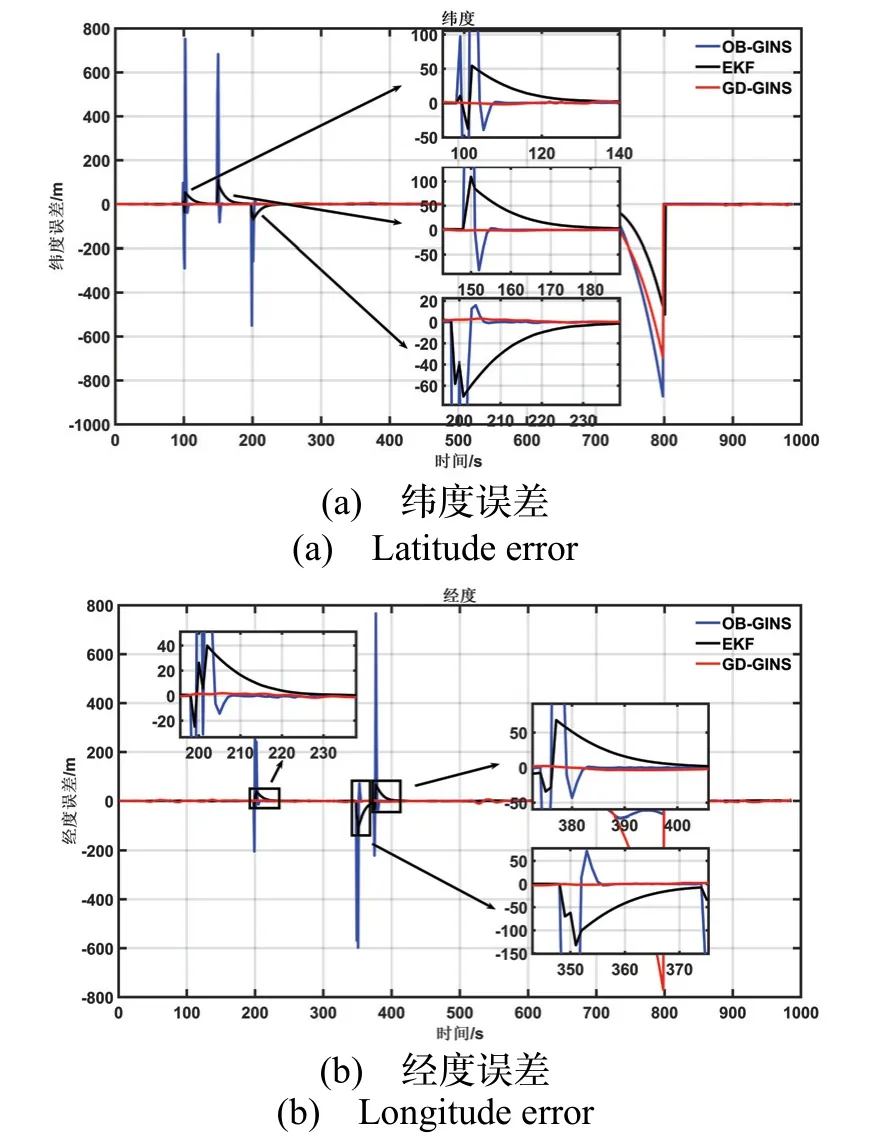
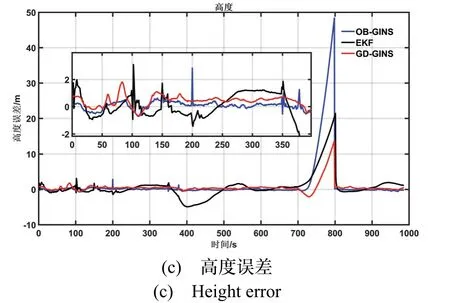
图7 实时状态估计对比图Fig.7 Comparison of state estimation under gross error interference

表2 所示，在卫星存在粗差的时间段GD-GINS相比OB-GINS，在纬度和经度方向上精度分别提升了97.92%和97.57%，相比EKF 在纬度和经度方向上精度分别提升了91.38%和90.81%。验证了本文提出的粗差检测窗口，能够有效地减少因卫星粗差造成的较大误差波动，实现状态估计的鲁棒性。

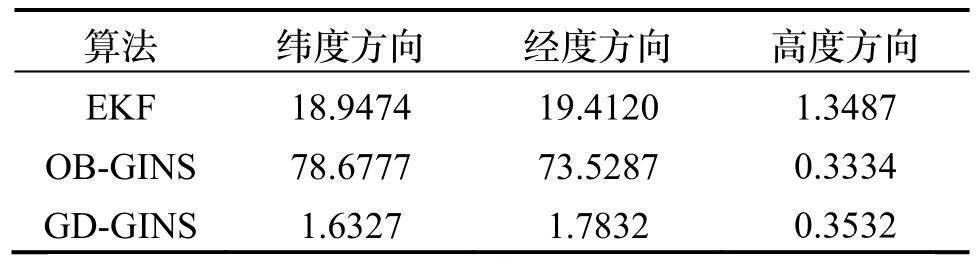
表2 粗差干扰下100-400 s 时间段位置估计误差标准差/mTab.2 The standard deviation of position estimation errors（100-400 s）under gross interference

EKF 算法的估计结果是不可逆的，而图优化算法可在卫星信号恢复后，对之前状态再优化，通过这种后处理手段，可极大提高卫星拒止时的估计精度。本文对卫星拒止时间段内的状态进行后处理，如图8 所示，GD-GINS 和OB-GINS 相对于EKF，估计更平滑，估计精度更高。

图8 GD-GINS 与EKF 优化效果比较Fig.8 Comparison of optimization effects between GD-GINS and EKF

经过后处理，表3 给出了GD-GINS 和EKF 在卫星中止阶段的状态估计误差对比情况，该图优化算法在卫星信号100 s 长时间拒止情况下，可通过后处理手段，使估计具有较强的鲁棒性和平滑性。相比于EKF，GD-GINS 可将位置估计误差降低30%以上。

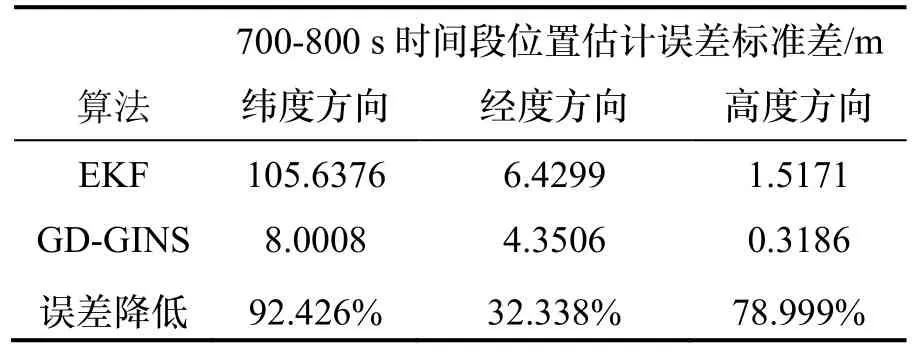
表3 GD-GINS 与EKF 位置估计误差的标准差统计Tab.3 The standard deviation statistics of position estimation error of GD-GINS and EKF

5 结论

本文针对城市复杂环境下的GNSS/INS 高精度鲁棒组合导航问题，提出了一种优化因子图数据融合算法。基于卫星信息关联性的特性，设计了一种滑动窗口粗差检测算法，实现卫星粗差检测与融合预处理，抑制粗差对导航结果的影响；构建考虑地球自转项的IMU 预积分因子、卫星位置、速度因子，提高了因子图优化模型精度。车载数据处理结果表明，GD-GINS的定位精度相比OB-GINS和EKF算法均有小幅提升；针对卫星信号中存在粗差的情况，GD-GINS 的定位误差精度相比OB-GINS 和EKF 算法提升90%以上,可以辅助导航系统获得较好的状态估计效果；针对GNSS拒止的情况，GD-GINS 的位置定位精度相比EKF 提升30%以上。