基于罗经/DVL/USBL组合导航系统的DVL在线标定算法

张 舸，谢阳光，伊国兴，李学成，王 尚

（1.哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001；2.中国航空工业集团公司 西安飞行自动控制研究所，西安 710065；3.中海辉固地学服务（深圳）有限公司，深圳 518067）

随着人类对海洋资源的开发与利用，海底地形勘探、管线巡检、资源开发、深海作战等都对水下定位导航技术提出了新的要求[1,2]，基于多传感器数据融合的水下组合导航系统是实现水下高精度导航的重要研究方向[3-5]。作为水下导航的重要传感设备，基于声学的多普勒计程仪(Doppler Velocity Log,DVL)通过向水底发射声波并分析其回波的多普勒频移来解算水下运载体相对于水底的速度，其测量误差主要由刻度因数误差和安装角度误差组成，对这两项误差参数的精确估计可以极大程度提高水下导航的精度。

J.Gong 等人提出了基于卡尔曼滤波器(Kalman Filter,KF)的DVL 在线标定算法，将DVL 的量测速度与捷联惯导系统(Strap-down Inertial Navigation System,SINS)的速度输出进行模型解算，获得误差参数的在线估计，标定后定位精度优于0.5%航程，但该算法的估计精度随着时间的增长逐渐降低[6]。J.Liu 等人在此基础上提出了基于全球导航卫星系统(Global Navigation Satellite System,GNSS)辅助下的三点在线标定方法，将终点定位精度提高至0.07%航程，但是该方法需要水下运载体进行两次上浮，不适用于大深度工作环境[7]。P.Liu 在此基础上提出了SINS/GNSS 辅助下基于KF 的DVL 在线标定算法，并通过可观测性矩阵分析了标定轨迹对DVL 误差参数估计精度的影响[8]。B.Xu 等人提出了SINS/GNSS 辅助下基于四元数的DVL标定算法，使安装误差角的估计精度得到大幅提高[9]。以上研究均是基于速度观测进行的DVL 标定，其估计精度和稳定性均受量测噪声影响，而B.Xu 等人提出了基于鲁棒不变扩展卡尔曼滤波算法的DVL 标定方法，通过引入李群理论有效降低了由DVL 量测异常值对标定精度的影响，有效提升了基于速度观测进行DVL标定的精度[10]。徐晓苏等人提出了SINS/GNSS辅助下基于梯度下降四元数的DVL 标定算法，在位置观测标定方法下安装角度误差估计精度提高至0.02 °度以内[11]。不同于以上传统的标定算法，J.Liu等人提出了基于遗传算法的DVL 误差参数标定方法[12]，D.Li 等人提出了基于粒子群优化的组合导航系统的DVL 标定方法[13]，B.Wang 等人提出了一种在SINS 辅助下基于GA-SVR 算法的回归预测器的无模型DVL 标定算法[14]，三者均能获得较高的估计精度，但对水下运载体的计算资源要求较高，且均为离线方法，在工程使用中仍有困难。

在工程应用中，出于对水下设备成本控制的考虑，采用了罗经代替惯导，与DVL 和超短基线定位系统（Ultra Short Base Line，USBL）组合导航。在该组合中，由于实际工况下USBL 的工作稳定性往往欠佳，且传感器数据波动较大，无法通过其位置差分获得有效的运载体速度数据，不能为标定DVL 提供有效的速度观测条件，因此无法采用传统基于速度观测的方法进行 DVL 误差参数的标定。本文基于罗经/DVL/USBL 的组合方式，将DVL 的误差参数通过罗经量测传播到航位推算位置信息中，并通过设计的双环路卡尔曼滤波器以基于USBL 位置观测的方式估计得到DVL 的误差参数和导航位置信息。

1 DVL 误差模型参数化表征

1.1 DVL 量测输出模型建模

DVL 是水下运载体的速度量测单元，根据其工作深度的不同输出水下运载体相对于水底或水流速度。本文涉及的遥控无人潜水器（Remote Operated Vehicle，ROV）工作在深度较大的海域，与海底之间的距离满足跟踪模式的工作阈值，DVL 输出ROV 相对于海底的速度信息。

DVL 的理想输出是基于 DVL 量测坐标系O-X d Yd Zd下水下运载体的三轴线速度Vd，当只考虑DVL 的安装偏角误差和刻度因数误差时，其与载体坐标系O-X bY b Zb下的理想速度Vb之间满足：

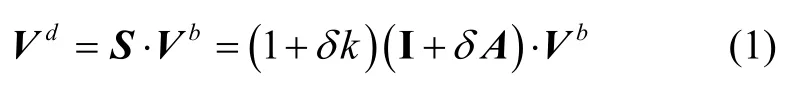
式中，kδ为DVL 的刻度因数误差，反映了DVL 输出值与真实值之间的比例误差，是传感器的固有特性，这里考虑三个方向的刻度因数误差为相同值。δ A为DVL 的安装角度误差矩阵，反映了由DVL 量测坐标系与载体坐标系各轴之间的偏角θdx、θdy、θdz产生的误差，其定义如式(2)所示，当ROV 处于定深度低速航行时，安装角度误差只考虑航向偏角的影响。

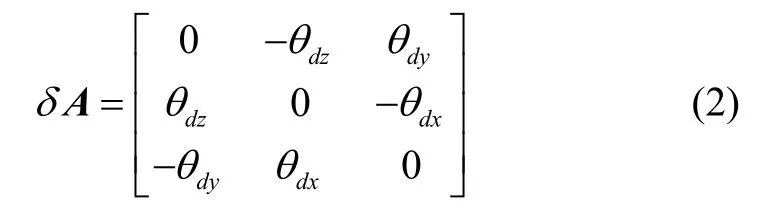
综上，DVL 的量测输出可表示为：

1.2 DVL 误差传播模型建模

根据上述的DVL 模型，对DVL 的标定即对刻度因数误差δk和z 轴安装角度误差θdz的估计。将这两个DVL 误差参数转化为组合导航系统状态变量的一部分，并分析其传播过程，则可以实现在ROV 组合导航解算的同时完成DVL 的在线标定。

给定初始位置，以DVL 和罗经的输出作为数据来源进行航位推算，在忽略其他影响因素的情况下，航位推算得到的位置与真实位置P之间的误差δ P可以认为是由DVL 的两个误差参数引起的，即DVL 的误差参数最终向组合导航系统位置误差传播。

组合导航系统的位置误差变化率如下所示：

其中，和分别表示基于DVL 输出计算得到的导航坐标系下的东向速度和北向速度。L和h分别表示ROV 当前所处的纬度和高度。Rm和Rn分别表示当前位置的子午圈地球曲率半径和卯酉圈地球曲率半径。

在式(4)中，位置误差转换矩阵和速度误差转换矩阵均可由导航系统当前的航位推算、DVL 速度量测等信息计算获得，位置误差δ P在计算中取自上一时刻的迭代值，导航坐标系下速度误差δVn的计算如式(8)所示。式中为基于罗经输出计算的方向余弦矩阵。Cφ为航向角量测噪声转换矩阵。wφ为罗经的航向角量测噪声，是标准差为σφ的高斯白噪声。

其中，航向角量测噪声转换矩阵Cφ是考虑罗经存在航向角量测噪声δφ时对方向余弦矩阵造成的影响，二者满足如下关系：

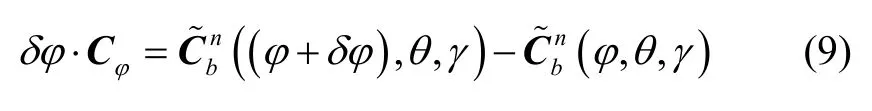
式中，φ表示航向角，θ表示俯仰角，γ表示滚转角。

为DVL 误差参数矩阵，其定义为：

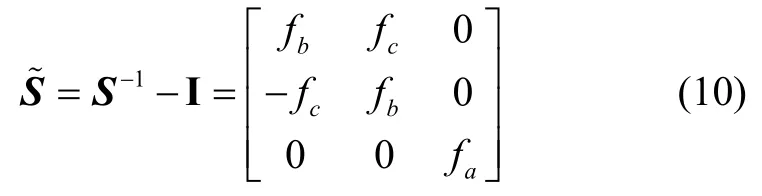
其中，误差参数矩阵中各元素的值为：

式中，D1为DVL 误差参数传递矩阵，D2为航位推算量测噪声传递矩阵，定义分别如式(13)(14)所示：

其中，VdT是DVL 量测数据转换矩阵，其定义为：

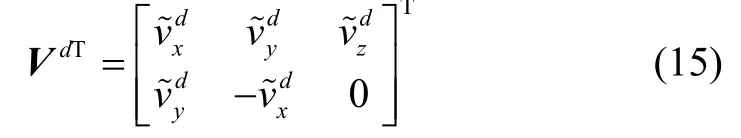
根据式(12)可知，DVL 的误差参数经过转化最终传播到位置误差的解算迭代过程中。

当组合导航解算迭代完成后，通过式(16)可以得到DVL 的刻度因数误差和z 轴安装角度误差。

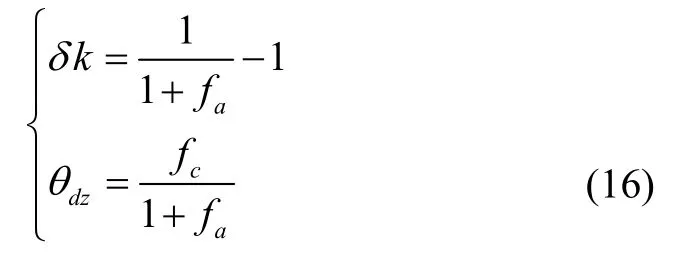
2 基于位置观测的DVL 标定与组合导航算法

如图1 所示，为基于位置观测的DVL 在线标定与组合导航算法框图。算法采用双环路卡尔曼滤波器架构，内环进行组合导航位置解算，外环进行DVL的误差参数估计，通过基于位置观测的DVL 误差传播模型设计卡尔曼滤波器，在实现ROV 的组合导航的同时进行DVL 的在线标定。

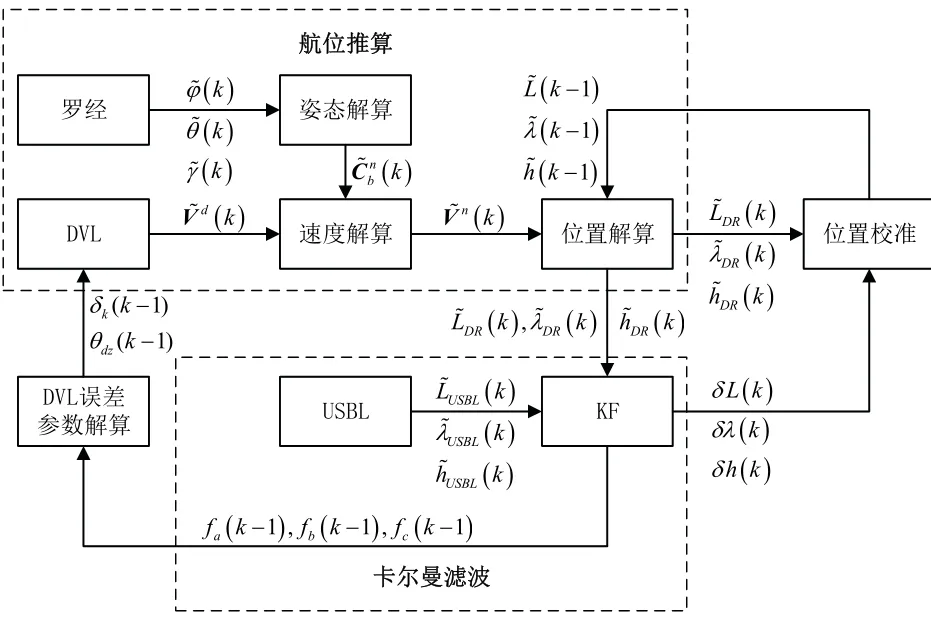
图1 DVL 在线标定组合导航系统框图Fig.1 Block diagram of DVL online calibration integrated navigation system

算法过程中，由罗经和DVL 组成的航位推算进行ROV 的位置更新与迭代，并与USBL 的位置量测在卡尔曼滤波器中进行数据融合进而得到平滑且不发散的组合导航位置。与此同时，基于USBL 的位置观测，卡尔曼滤波器将传播到航位推算中的DVL 误差参数进行估计解算并反馈给ROV 的速度解算过程，在不断的迭代中，算法逐渐稳定，滤波器将输出满足精度要求的DVL 误差参数估计值。

2.1 状态方程

选择DVL 的误差参数向量和ROV 的位置误差作为状态变量，即：

式中，Lδ、δλ和hδ分别为ROV 航位推算位置的纬度误差、经度误差和高度误差。

则DVL 在线标定组合导航系统的状态方程为：

2.2 量测方程

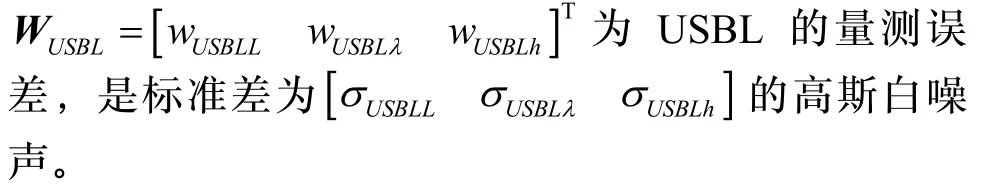
2.3 可观测性分析

根据分段线性定常系统（PWCS）的可观测性分析方法，系统被分为若干个时间段，在每一个时间段内，状态转移矩阵和量测矩阵均为常值，因此可以根据系统的状态转移矩阵和量测矩阵得到k时段导航系统的可观测性矩阵为：

组合导航系统的全局可观测性矩阵可由各时段的可观测性矩阵构成，如下所示：

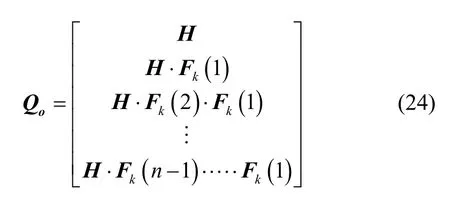
当系统采样时间为1 s，ROV 以1 m/s 的前向速度并保持30 °航向角进行7200 s 匀速直线运动时，对其全局可观测性矩阵进行SVD 分解，得到5 个奇异值分别为170.57、84.87、84.84、52.01 和0.03。

如图2 所示，为DVL 在线标定组合导航系统全局可观测性矩阵Qo经过SVD 分解后所得右奇异值矩阵V中各奇异值对应其正交基元素的取值分布。其中横坐标表示奇异值的序号，即矩阵V的列序号，纵坐标表示各列向量元素的取值。根据系统状态变量的顺序，图中的蓝色、橙色、黄色、紫色和绿色柱形分别代表刻度因数误差、安装角度误差、纬度误差、经度误差和高度误差相关量。由柱形图的分布可以得知，第一个奇异值170.57 对应刻度因数误差的可观测度，第二奇异值84.87 对应经度误差的可观测度，第三个奇异值84.84 对应纬度误差的可观测度，第四个奇异值52.01 对应高度误差的可观测度，第五个奇异值0.03对应安装角度误差的可观测度。由于系统状态变量的量纲不同，其奇异值的大小不能直接作为比较其可观测度的依据，只能证明在该条件下系统的五个状态变量是完全可观的。

图2 DVL 在线标定组合导航系统可观测度分析Fig.2 Observability analysis of DVL online calibration integrated navigation system

3 仿真验证

3.1 仿真条件与精度评价指标

为了验证组合导航系统能够在进行组合导航位置解算的同时在线估计DVL 的误差参数，进行了相关仿真实验，仿真条件如下：

a) ROV 的起始位置为东经 116.35 °，北纬39.98 °，高度-1000 m；

b) ROV 保持前向速度1 m/s，航向角30 °进行匀速直线运动；

c) DVL 量测噪声各轴标准差均为0.1 m/s，刻度因数误差0.015，z 轴安装角度误差0.75 °；

d) 罗经量测噪声各轴标准差均为0.1°；

e) USBL 量测噪声水平方向标准差为1 m，高度方向标准差为0.1 m；

f) 系统采样周期为1 s，仿真时间7200 s。

对于导航算法的定位精度，本文同时采用终点相对精度和全局相对精度来进行表征。终点相对精度是指，在导航结束时由导航算法解算的位置与真实位置之间的距离与总航程之比，该指标仅能反映导航算法在导航终点的定位精度，无法反映导航过程中算法的稳定性。全局相对精度是指，在导航过程中的每一个时段，计算其相对定位精度并在导航结束后对所有时段的导航精度求平均值，如式(24)所示，该指标一定程度上反映了导航算法的精度和稳定性。

对于DVL 误差参数的估计精度，一方面由算法估计值直接反映，另一方面将估计值对DVL 模型进行校正，并计算校正后的航位推算数据，将定位精度与校正前对比可间接反映DVL 误差参数的估计结果。

3.2 仿真结果与分析

图3 是仿真实验中DVL 刻度因数误差和z 轴安装角度误差的估计结果，具体数值如表1 所示。

图3 DVL 误差参数估计Fig.3 Estimation of DVL error parameter

表1 仿真实验DVL 误差参数Tab.1 DVL error parameters in simulation experiment

由表1 可知，在基于组合导航位置观测的DVL标定算法估计结果中，刻度因数误差最终收敛于0.0157，z 轴安装角度误差最终收敛于0.8381 °。与仿真设定值相比，估计结果基本达到要求。

传统基于速度观测的DVL 标定算法中，z 轴安装角度误差的估计值为0.7975 °，略优于前者，刻度因数误差的估计值为-0.7567，显然与实际情况不符。由于观测速度引入了USBL 的圆概率误差，在ROV 低速行驶的情况下，有效数据被误差淹没导致该算法无法正确估计刻度因数误差的值。

因此基于速度观测的DVL 标定方式不适用于罗经/DVL/USBL 组合导航系统中，而基于位置观测的DVL 标定方式则能够有效地规避直接观测速度带来的误差，采用双环路卡尔曼滤波器架构通过对组合导航位置的解算与观测完成对DVL 误差参数的有效估计。

图4 是仿真实验中ROV 的真实运动轨迹、USBL量测轨迹、组合导航解算轨迹以及DVL 标定前后航位推算轨迹对比图。图中，DVL 标定之前的航位推算轨迹随着时间的增长逐渐偏离真实轨迹；USBL 的量测轨迹虽然没有发散，但围绕真实轨迹有较大波动；组合导航解算轨迹与真实轨迹具有较高重合度且相对USBL 数据更加平滑；DVL 标定后的航位推算轨迹虽未随时间增长而发散，但与真实轨迹仍有一定误差。

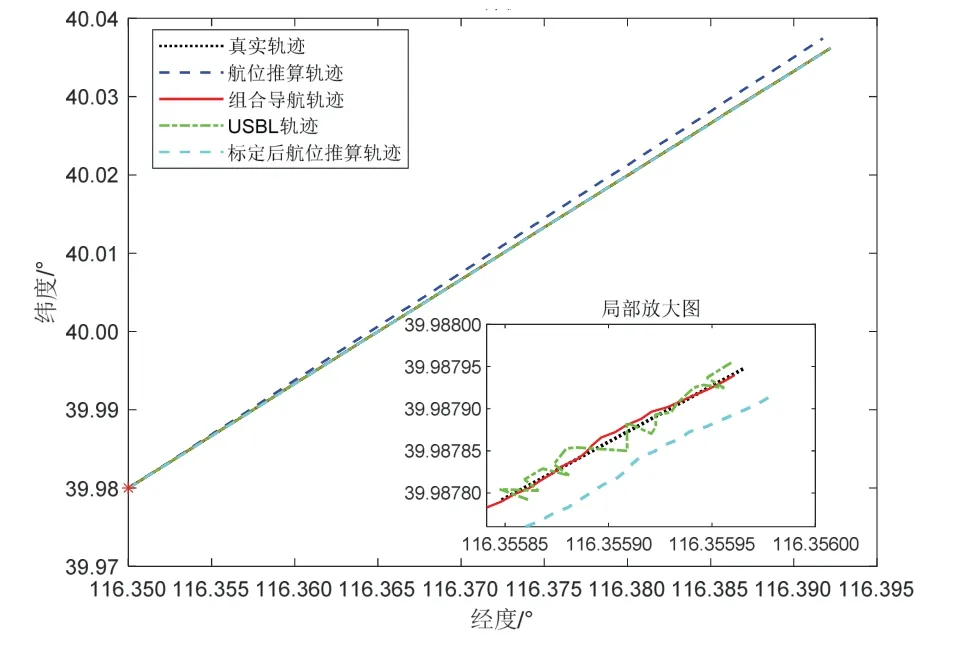
图4 仿真实验轨迹对比Fig.4 Comparison of tracks in Simulation experiment

图5 是仿真实验中组合导航以及DVL 标定前后航位推算解算位置与真实位置之间的误差。图中，DVL 标定之前的航位推算轨迹随着时间的增加，其定位误差逐渐累积且最终发散；组合导航与DVL 标定之后航位推算的定位误差均未发散，但航位推算的定位误差略大于组合导航，具体定位精度如表2 所示。

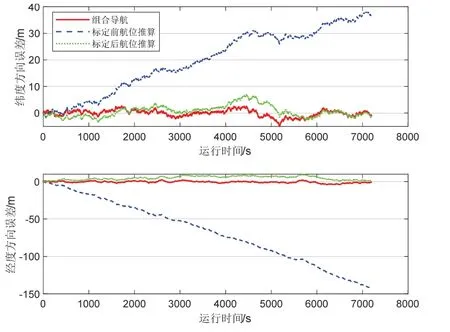
图5 仿真实验定位误差对比Fig.5 Comparison of positioning error in simulation experiment

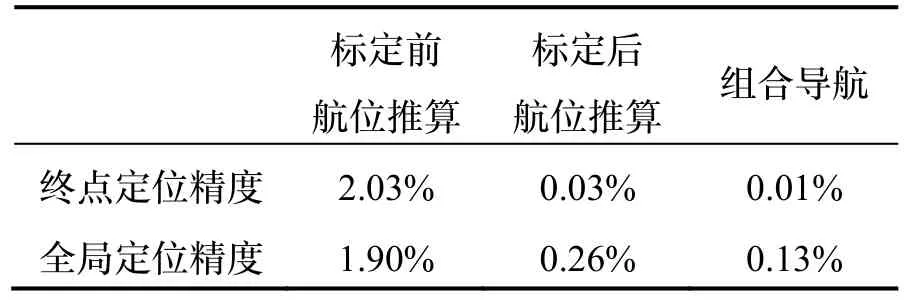
表2 仿真实验导航定位精度Tab.2 Accuracy of navigation in simulation experiment

根据定位精度的计算结果可以证明，在仿真实验中DVL 在线标定组合导航算法解算得到的位置具有较高定位精度和算法稳定性，同时该算法估计得到的DVL 参数误差能够较好地补偿航位推算的定位误差，使DVL 标定后的航位推算的定位精度大幅提升，并具有良好的算法稳定性。

3 海试验证

3.1 测试条件

为了验证DVL 在线标定组合导航系统的实用性，2021 年11 月在南海某海域利用ROV 进行了试验。现场配置状态如图6 所示。

图6 海试ROV 传感器配置Fig.6 Configuration of ROV sensors in sea trial

具体测试传感器设备条件如下：

a) CFCV1500 型ROV 设备，作业水深可达1500 m，速度最高3 节；

b) 全国产化320B 型光纤罗经设备，航向角量测精度优于0.3 °；

c) RDI 1200kHz navigator 型DVL 设备，长时精度约为±0.2%±0.1 cm/s；

d) Sonardyne Ranger 2 HPT 5000 型USBL 设备，定位精度优于15 mm。

3.2 测试结果与分析

图7 和图8 分别为海试过程中罗经、DVL和USBL的有效量测数据，由量测数据可知，ROV 在海试过程中保持245 °左右的航向角向西南方向大致以0.2 m/s的速度运动。

图7 海试罗经与DVL 有效量测数据Fig.7 Measurement data of compass and DVL in sea trial

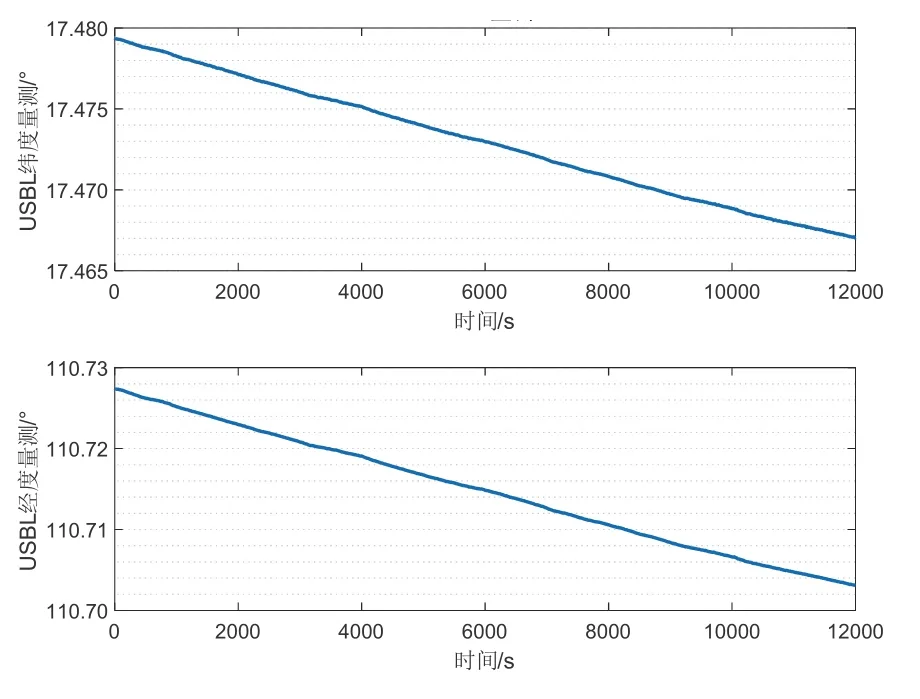
图8 海试USBL 有效量测数据Fig.8 Measurement data of USBL in sea trial

图9 是海试中DVL 刻度因数误差和z 轴安装角度误差的估计结果，其中刻度因数误差最终收敛于0.0043，z 轴安装角度误差最终收敛于-1.9641 °。在无法验证其真实值的情况下，DVL 误差参数的估计精度只能以标定后航位推算的定位精度间接体现。

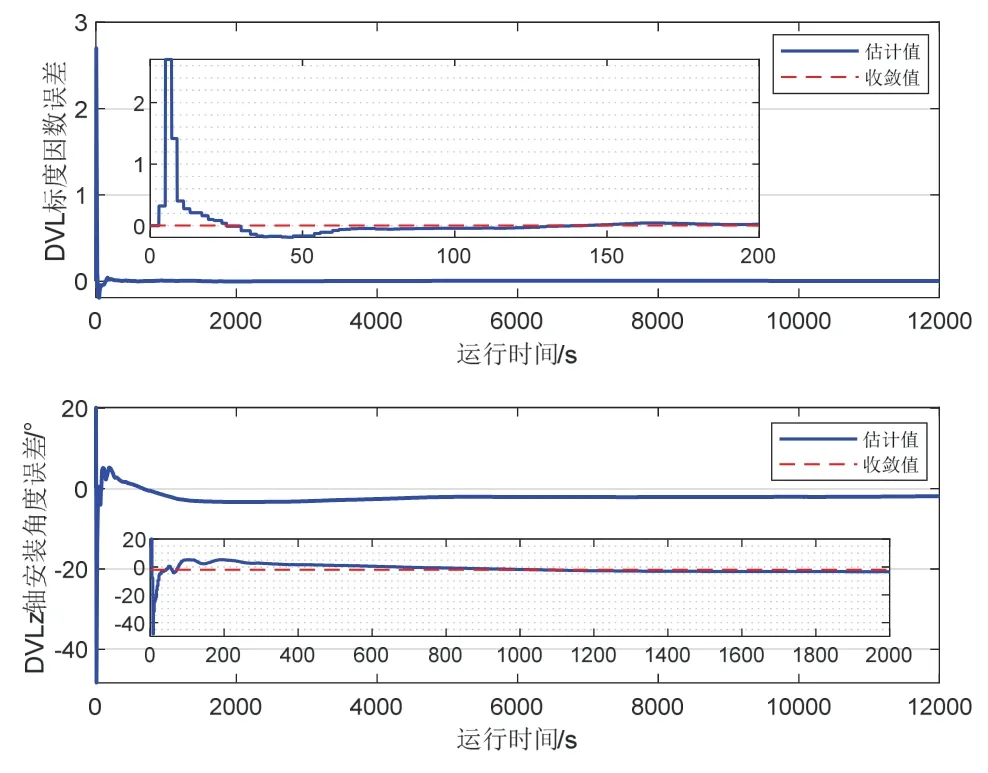
图9 海试DVL 误差参数估计Fig.9 Estimation of DVL error parameter in sea trial

图10 是海试中ROV 的USBL 量测轨迹、组合导航解算轨迹以及DVL 标定前后航位推算轨迹对比图。图中，USBL 的量测轨迹波动较强，但依据传感器的固有特性，其量测结果始终不会发散；组合导航解算轨迹与USBL 轨迹具有较高重合度，且比USBL 数据更加平滑，可以作为ROV 的真实位置估计；DVL 标定之前的航位推算轨迹随着时间的增长逐渐偏离USBL 的量测轨迹；DVL 标定后的航位推算轨迹虽然没有随时间增长逐渐发散，但与USBL 量测轨迹和组合导航解算轨迹之间有明显误差。

图10 海试轨迹对比Fig.10 Comparison of tracks in sea trial

图11 是海试中DVL 标定前后航位推算解算位置与组合导航解算位置之间的误差。图中，DVL 标定前的航位推算轨迹随着时间的增加，其定位误差逐渐累积且最终发散；DVL 标定后航位推算的定位误差得到了显著抑制，具体定位精度如表3 所示。

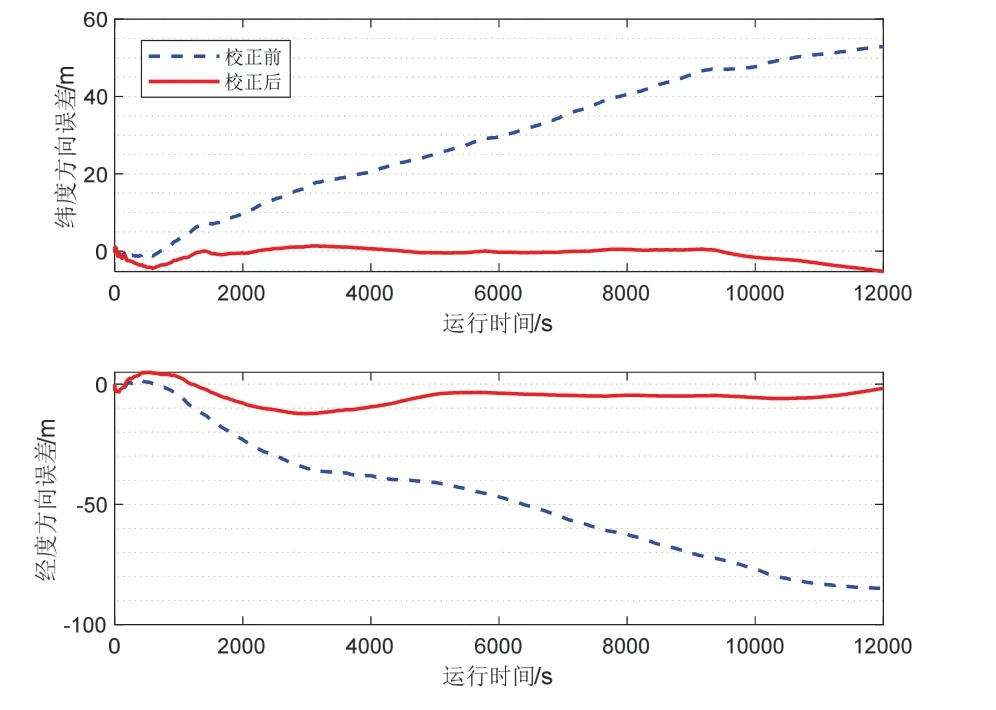
图11 海试定位误差对比Fig.11 Comparison of positioning error in sea trial

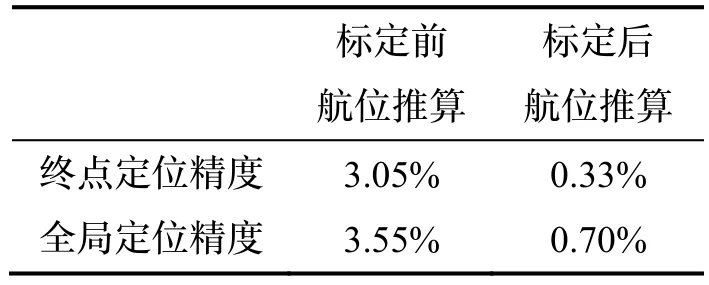
表3 海试导航定位精度Tab.3 Accuracy of navigation in sea trial

根据USBL 量测轨迹与组合导航解算轨迹的分析可以证明，在海试中DVL 在线标定组合导航算法解算得到的位置具有较高定位精度和算法稳定性。根据定位精度的计算结果可以证明，在海试中DVL 在线标定组合导航算法估计得到的DVL 参数误差能够较好补偿航位推算的定位误差，标定后航位推算的定位精度大幅提升，并具有良好的算法稳定性。

4 结论

针对大深度水下工作环境中ROV 组合导航与DVL 标定问题，本文提出了一种基于罗经/DVL/USBL组合导航系统的DVL 误差参数在线标定算法，通过建立DVL 的刻度因数误差和安装角度误差的传播模型，将DVL 的误差参数引入基于罗经和DVL 的航位推算的迭代中，并以USBL 的位置输出作为观测量，对包括DVL 误差参数和航位推算定位误差在内的状态变量进行卡尔曼滤波，进而实现ROV 组合导航输出的同时进行DVL 的在线标定。

仿真结果表明，组合导航位置输出的终点相对定位精度为0.01%总航程，全局相对定位精度为0.13%总航程；DVL 刻度因数的估计值为0.0157，估计精度优于0.0007；z 轴安装角度误差的估计值为0.8381 °，估计精度优于0.09 °；以估计值对DVL 进行标定后航位推算的终点相对定位精度由2.03%总航程大幅提高至0.03%总航程，全局相对定位精度由1.90%总航程提高至0.26%总航程。海试结果表明，组合导航位置输出与USBL 的位置量测具有较好的重合度，且轨迹曲线较为平滑；DVL 刻度因数的估计值为0.0043，z 轴安装角度误差的估计值为-1.9641 °；以估计值对DVL 进行标定后航位推算的终点相对定位精度由3.05%总航程大幅提高至0.33%总航程，全局相对定位精度由3.55%总航程提高至0.70%总航程。证明本文提出的基于ROV组合导航系统的DVL 在线标定算法能够在输出组合导航位置的同时进行DVL 标定，且具有较高的导航定位精度、DVL 误差参数估计精度和算法稳定性。

本文只对DVL 的z 轴安装角度误差进行了估计，同时在误差传播函数推导过程中忽略了安装角度误差的二阶小量，后续的研究将在此基础上建立更精确的误差参数传递模型，并考虑在复杂运动轨迹下对DVL的全部安装角度误差进行更高精度的估计。