平稳随机载荷的灵敏度分析识别方法

夏 鹏， 杨 特， 王 乐, 杨智春

(1. 西北工业大学 航空学院， 西安 710072； 2. 上海机电工程研究所， 上海 201109)

动载荷识别方法通过结构响应信息对结构所受动载荷进行识别，最早于20世纪70年代中期在航空领域被提出，目的在于更准确地获取飞机在飞行过程中的受载情况。经过几十年的发展，国内外学者针对动载荷识别问题开展了大量的基础理论研究和工程应用研究工作，使动载荷识别方法得以不断的创新与完善，并在各个工程领域中得到应用。目前，动载荷识别方法主要分为频域法和时域法，分别在频域和时域中对动载荷进行识别。

动载荷频域识别方法是发展较早、较为成熟的识别方法。Barlett等[1]最早利用频域直接求逆法，识别出直升机桨毂中心在主要谐波频率下的动载荷。之后Hansen等[2]提出频响函数矩阵直接求逆法在共振区附近接近病态，导致识别载荷的误差较大。针对这种现象，一些学者将数学反问题求解理论应用于动载荷识别方法。Karlsson等[3-4]国内外学者针对频响函数矩阵病态问题进行了较为深入的研究，提出了一些改进的频响函数矩阵求逆方法。Jia等[5-6]同时考虑FRF和响应误差，利用5个加速度传感器信号，分别将加权正则化方法和总体最小二乘方法应用于识别作用在平板结构的三个平稳随机动载荷，其正则化参数由广义交叉检验准则(generalized cross validation，GCV)确定。总的来说，动载荷频域识别方法，原理简单且识别精度良好，但得到的结果为频域结果。由于载荷的识别过程需要在频域中进行，需要足够长度的测试样本数据才能保证数据的稳定性，所以只适用于持续时间长的确定性动载荷及随机动载荷样本的识别，而对冲击载荷这类瞬态载荷，其识别效果较差。

与频域动载荷识别方法相比，时域法研究相对较晚，但时域识别结果直观、便于应用，无需在频域内进行傅里叶变换，不需要大量的统计数据，误差也较小，在识别冲击载荷之类的非平稳载荷上较之于频域法优势明显，受到工程界的青睐。随着系统辨识技术、控制理论的发展，结构动力学方程的多种求解方法也发展起来。Law等[7]提出了状态空间形式的移动载荷识别方法，并利用动态规划法解决识别结果扰动过大的问题。Jiang等[8-9]针对模态函数在结构约束边界为零的现象，将空间分布载荷在Legendre多项式空间展开，并成功应用于Euler梁上空间分布动态载荷和作用于薄板上的空间分布载荷。陈帅等[10-11]基于模态空间转换、离散数据最小二乘拟合与模态叠加原理,提出一种动载荷时域半解析识别方法，并准确识别出了作用于悬臂板结构上的平稳随机动载荷。该方法中首次提出了将动载荷进行“分段识别”的概念，也证明了动载荷分段识别方法具有良好的应用潜力；之后，针对随机载荷的识别，Li等[12]提出了一种基于谱分解和正则化的时域随机动载荷识别方法，将随机动态载荷识别转化为载荷均值函数识别和协方差矩阵重构。方法基于格林核函数法建立前向辨识模型，进行谱分解，将动载荷协方差矩阵的辨识转化为一系列特征向量的辨识，经仿真算例与试验验证，对于随机载荷实现了很好的识别效果。该方法直接针对于随机载荷的特征进行识别，是一种高效的随机载荷频域识别方法。而针对随机动载荷的时域识别，Liu等[13]基于Gegenbauer多项式展开理论和正则化方法，在时域中将动载荷表示为时间和随机参数的函数，通过离散化的负荷卷积积分和相应的系统单位脉冲响应函数，提出了一种识别随机结构动力荷载的解析方法。该方法基于结构动力学原理对动载荷进行解析识别，对于随机动载荷通常难以在时域内识别的问题提出了一种有效的解决方法；对于分布式随机载荷，Liu等[14]提出了一种新的基于盲源分离和正交匹配追踪的时空耦合分布动载荷识别方法。通过适当的正交分解，将时空耦合分布动荷载分解为一系列独立的空间分布函数和时程函数，采用格林核函数法和正则化方法进行识别。之后引入盲源分离技术进行时程函数的辨识。经算例验证，该方法能处理复杂结构上的时空耦合分布动荷载，并能分别实现其空间分布表示和时程重构。此方法的提出有效的应对了分布式动载荷难以表征、难以在时域内识别其时间历程的难题，对于分布式动载荷的识别问题具有重要的意义。

灵敏度分析是研究与分析一个系统(或模型)的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。毛玉明等将灵敏度分析技术引入动载荷识别领域，提出了基于灵敏度分析的动载荷时域识别方法，对作用于四自由度离散振动系统的正弦函数周期载荷进行了准确识别，且研究发现，利用灵敏度分析识别动载荷的方法对响应测量噪声不敏感[15]。

本文针对平稳随机动载荷的时域识别问题，提出一种基于灵敏度分析的平稳随机动载荷分段时域识别方法。将平稳随机动载荷样本分为若干小段，将该时间段内结构的输入动态载荷表示为正弦级数叠加的形式，针对灵敏度分析对初值敏感问题，提出选取频率参数的方法，提高了初值赋予的合理性，在一定程度上降低甚至避免了由于灵敏度分析初值敏感而导致识别结果不收敛或识别过程中迭代次数多、计算效率低的问题；并通过灵敏度迭代分析来确定相应正弦级数的幅值，从而确定该时间段内结构所受的平稳随机动载荷样本。最后将各个时间段平稳随机动载荷样本进行整合，得到平稳随机动载荷整体样本的识别结果。

1 动载荷灵敏度识别模型

对于线性多自由度系统，其运动方程可表示为

(1)

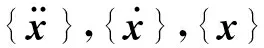
假设稳态随机动载荷{F}在第j个自由度上的激励Fj可以用若干个正弦函数的叠加的形式表示，即

(2)

(3)

(4)

(5)

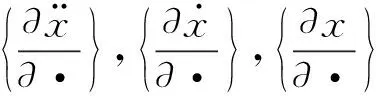
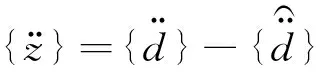
(6)

根据灵敏度定义可得

{δz}=[S]{δP}

(7)

式中：{δz}为加速度响应误差；{δP}是动态载荷参数向量的修正变化量；[S]是结构动响应对动态载荷参数的灵敏度矩阵。将式(7)展开可得

(8)

式中，l为分析时间段内采样时间点个数。同理，当已知结构某自由度上的位移响应或者速度响应，式(7)变为如下形式

(9)

(10)

式(7)可通过求灵敏度矩阵的广义逆，得到外激励参数向量的修正变化量{δP}，即

{δP}=[SHS]-1SH{δZ}

(11)

已知第j步中的载荷参数向量为{Pj}，其对应的修正变化量为{δP}，那么修正后的载荷参数向量{Pj+1}为

(12)

如果当前迭代步中的变化量小于一定的阈值，可以认为灵敏度迭代分析得到收敛。这里，将动载荷识别灵敏度迭代分析模型的收敛条件设置为

(13)

式中，μ为设定的阈值。

2 正则化方法

一般情况下，式(11)的求解中都会遇到不适定问题，即灵敏度矩阵为病态矩阵，从而导致解{δP}对于{δz}中的误差很敏感。因此可以采用Tikhonov正则化的思想[16]，将式(7)不适定问题转化为以下的阻尼最小二乘问题：

(14)

式中，λ是正则化参数。

通过调整正则化参数λ，可得出正则化解{δP}，则上述的优化问题式(14)可转化为如下形式

(15)

通过化简式(15)可得：

{δP}=(SHS+λ2I)-1SH{δz}

(16)

合理地选取正则化参数是正则化有效求解的关键。当选取的正则化参数较大，正则化解变偏离了原问题；当正则化参数较小时，正则化解仍是不稳定的。本文正则化参数λ通过GCV方法来选取。

3 平稳随机载荷样本的分段识别方法

对于工程结构所受到的一段平稳随机动载荷，我们很难用一系列的参数来表示它的时间进程。为了能将平稳随机动载荷样本进行参数化表示，可以将随机信号分割为若干小段，这样就能够用正弦函数叠加的形式来表示这一小段时间内的平稳随机动载荷样本，通过灵敏度迭代分析方法来确定相应正弦函数的参数，从而确定该时间段内结构所受的平稳随机动载荷。

对一小段平稳随机动载荷样本运用灵敏度分析模型进行识别时，很难得到收敛结果。这是因为当一小段载荷信号不存在周期性时，用多个正弦函数叠加方式去描述其时间历程，有无穷多的频率幅值组合能满足要求，即存在无穷多解，导致在灵敏度迭代分析时不能得到收敛结果。实际上，如果需要描述一小段随机样本，只需要一组正弦函数组合来表示即可。因此，在对一小段随机样本进行灵敏度分析时，只需要对特定频率下的幅值参数进行灵敏度分析，迭代求得特定频率下的正弦函数幅值。在选取频率点时，主要关注响应频率谱以及结构的固有频率，即：若响应频带范围内没有结构的固有频率，则在响应频率谱各个峰值的位置选取频率点作为主要频率点，若包含了固有频率，则在固有频率峰值半功率带宽内选取3～5个点作为主要频率点。最后在响应频带范围内均匀地布置若干个频率点，配合之前确定的主要频率点组成进行幅值灵敏度迭代分析所需的频率。

由于实际测到的结构振动响应是连续的，若要对每一时间段进行灵敏度分析，就需要消除待识别时间段之前动载荷对当前时间段响应的影响，从而保证每段的识别精度。本文采用的解决办法，在计算结构响应时，将已完成识别时间段的载荷与待识别时间段的由待识别载荷参数向量P决定的迭代载荷一起作为结构的载荷输入，利用公式(1)中的振动方程计算得到结构在完成识别时间段的载荷与待识别时间段载荷共同激励下产生的全时段响应。同时，在灵敏度分析时只需关注待识别时间段的响应误差，而待识别段响应误差是由该段时间计算响应与真实响应做差得到，由此可以消除该时间段之前的载荷对该时间段响应的影响。在选定频率点后，只对幅值参数进行灵敏度分析迭代能够快速收敛，因此幅值参数的初值不需要进行特殊设置。

平稳随机动载荷样本灵敏度分析方法的识别流程如下：

(1) 获取平稳随机信号激励下结构的振动响应；

(2) 对振动响应进行频谱分析，选定灵敏度迭代分析所需的频率点；

(3) 设定灵敏度分析中的初值，随机响应信号的分段数以及灵敏度分析迭代的收敛条件；

(4) 假设响应信号每段分析时长为Δt，对于第k段时间段[(k-1)Δt+1,kΔt]，由载荷参数得到该段假设载荷，将前k-1段[0,(k-1)Δt]的识别结果与第k段的假设载荷组合，求得总时长为的振动响应；

(5) 由结构真实响应与计算得到的仿真响应求得第k段的误差矩阵，根据灵敏度分析模型，迭代求得第k段假设载荷。检查是否满足收敛条件，若满足则得到该段的识别结果，若不满足则返回第4步；

(6) 将所有时间段的识别结果进行组合，得到该随机信号样本的识别结果。

4 试验验证

为了验证本章所提出的平稳随机动载荷识别方法的可行性和有效性，如图1所示。 采用一个框架模型来进行所提出方法的验证试验，根据测试的振动响应来进行平稳随机动载荷样本的识别。根据框架模型的特点，可以认为框架每层的质量都集中在每层的方框上，每两层方框之间由4个支柱进行连接，每个支柱是由截面为0.139 m×0.027 m × 0.001 m的扁钢条层叠而成。试验中采用1个垂直作用于框架结构的电磁激振器来施加各态历经的平稳随机动载荷。同时，在各层框架上分别布置加速度传感器。加速度传感器采用的PCB公司333B30型加速度传感器，灵敏度为100 mV/g，电磁激振器采用的是MB公司的Modal-50型电磁激振器，功率放大器采用的是MB公司的SL500 VCF型功率放大器，力传感器采用PCB公司208C02型力传感器，用于采集加速度与力信号的仪器为DEWESoft公司SIRID-8×STGM-8×AO型多功能采集仪，采样频率为500 Hz。试验布置如图2所示。

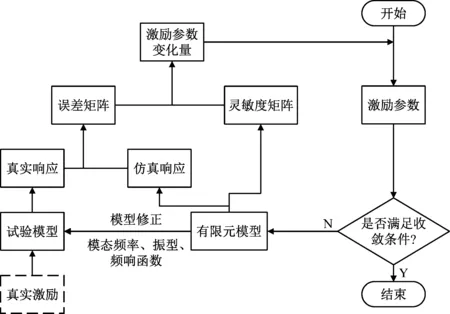
图1 动载荷识别流程

在灵敏度迭代分析过程中，需要尽量保证计算响应的仿真模型与实际模型尽可能一致[17]，因此对本文的试验模型进行动力学模型修正，经过修正后的计算模型与试验模型固有频率比较结果如表1所示。试验通过安置在激振器顶杆与框架第一层之间的力传感器以及各层的加速度传感器来获取力信号和加速度信号，各信号经过A/D转换后输入计算机，在识别过程中选用第2层以及第7层的加速度响应来进行载荷识别，结构所受的随机激励以及2个测点的加速度响应的时域信号如图3～4所示。对于随机动载荷进行片段分割时，分割的片段时间长度应当不小于结构动响应最低峰值频率对应周期的长度。而在完成各段动载荷识别后，段与段之间存在不连续情况时，将端点值取平均值后进行连接。

1-功率放大器； 2-电磁激振器； 3-数据采集仪； 4-计算机； 5-力传感器； 6-加速度传感器

表1 模型修正结果对比

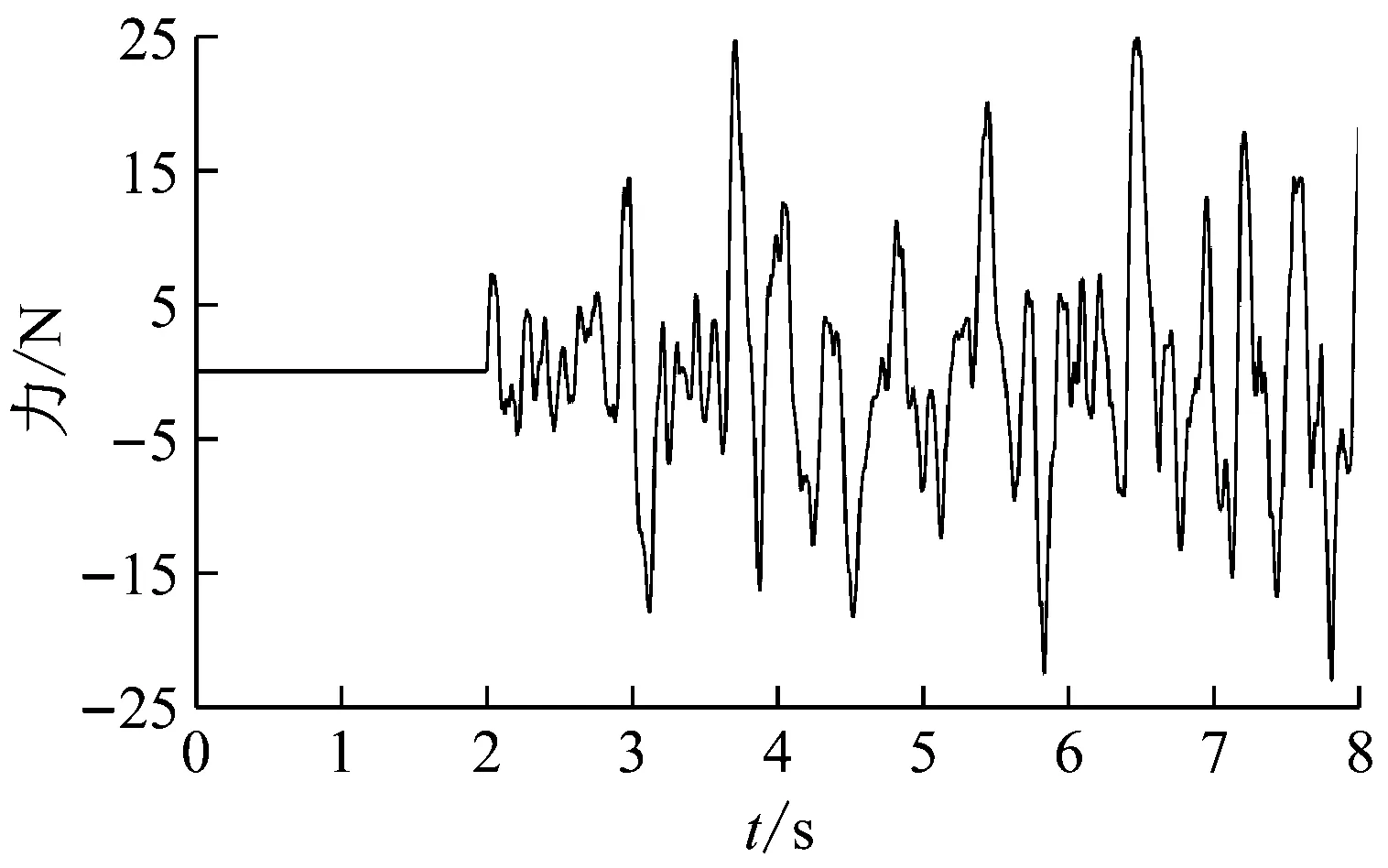
图3 平稳随机载荷样本

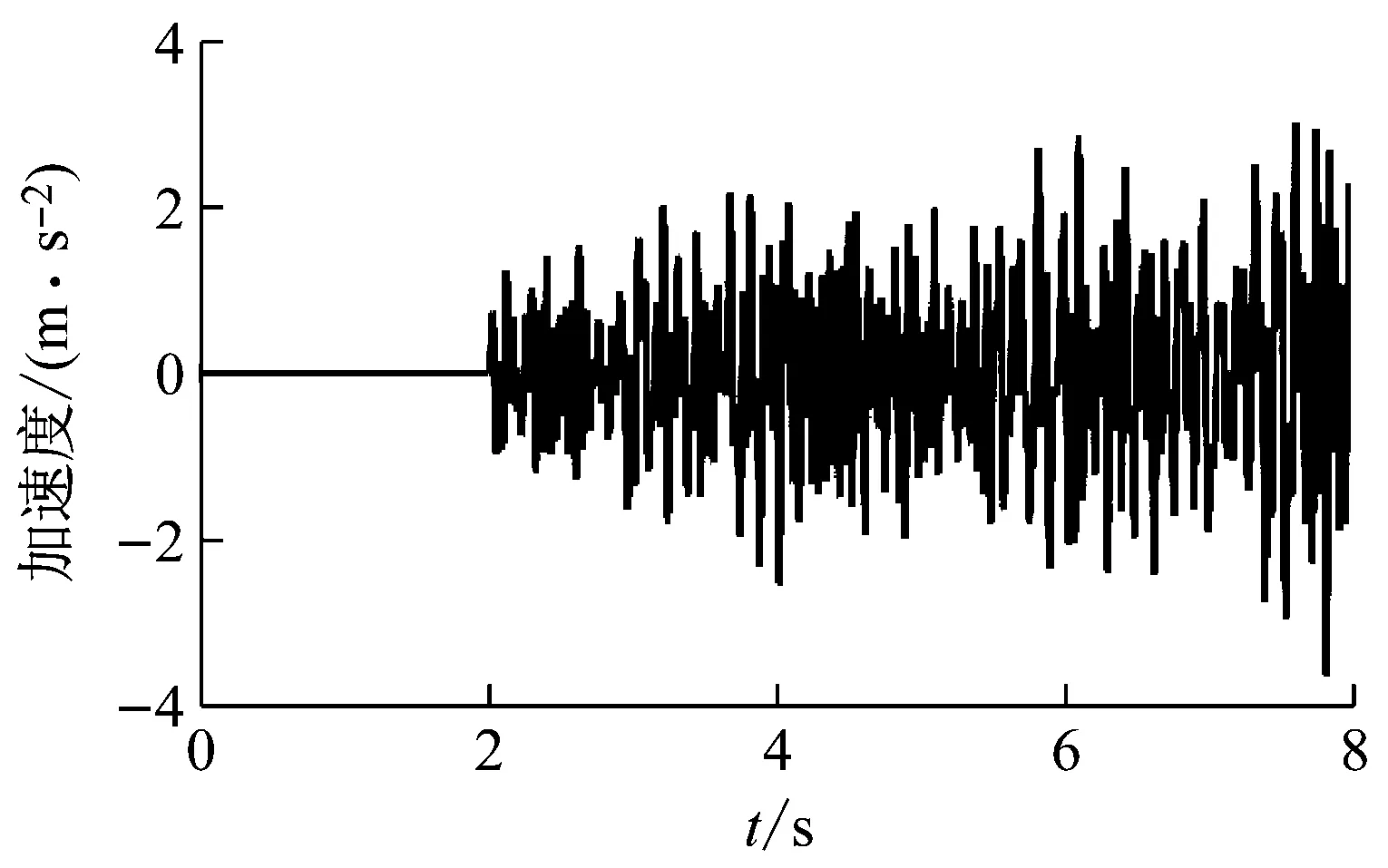
(a) 第2层测点加速度响应

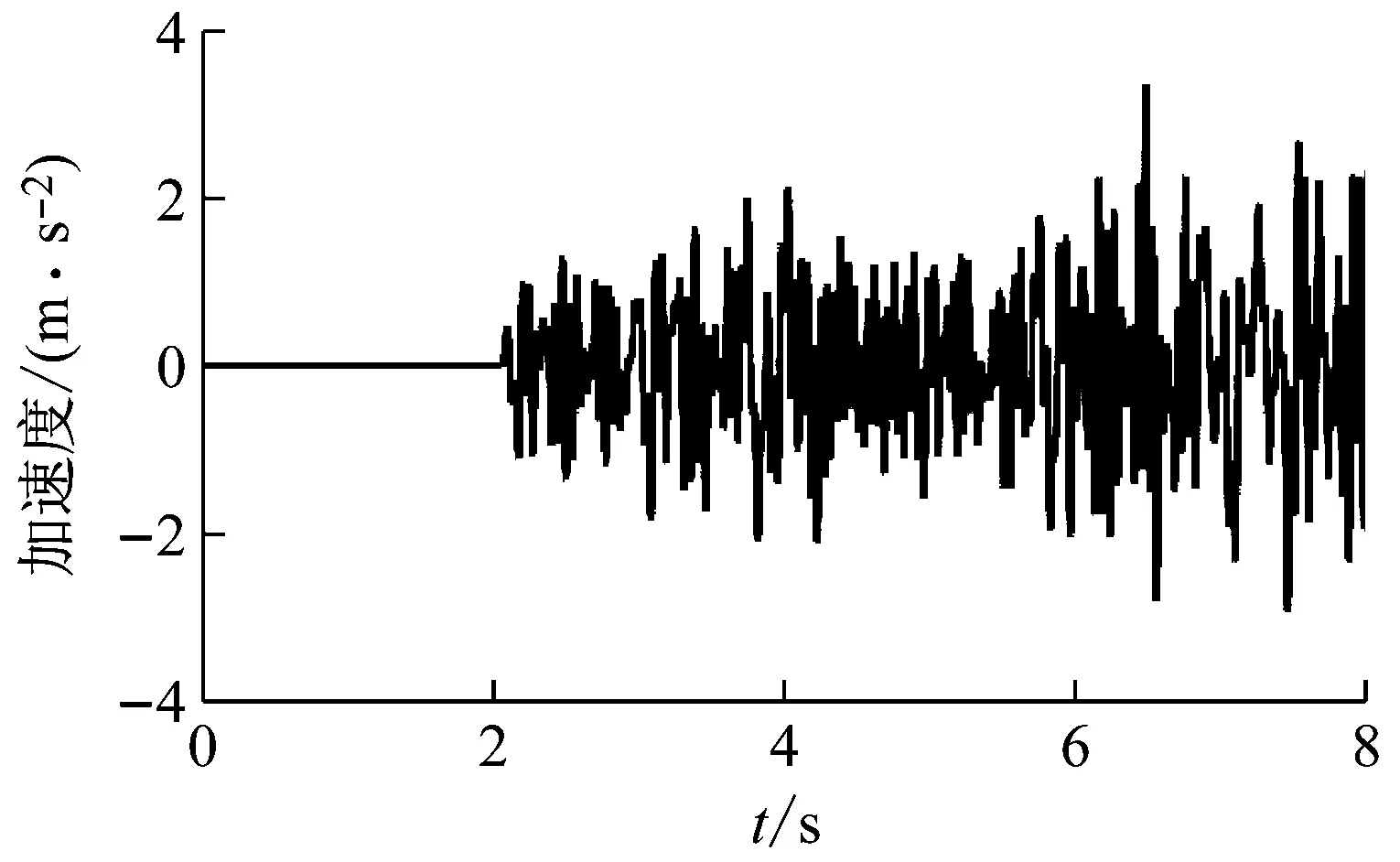
(b) 第7层测点加速度响应

对2个测点的加速度响应信号进行谱分析，来确定幅值灵敏度分析时需要的各个频率点，2个测点的自功率谱密度函数如图5所示，各个峰值坐标位置均在图中用黑点标注。可以看出，响应的频带范围为0～25 Hz，且在2.441 Hz、5.371 Hz、6.836 Hz、7.813 Hz、11.23 Hz、17.58 Hz、18.55 Hz、21.97 Hz以及23.93 Hz处存在峰值。平稳随机载荷，其本身类似白噪声。加上因为是线性系统，其激励起响应的频率应是相似的。因此结构响应和测量噪声混杂的时候，为准确有效挑出真实信号的频率点，本文挑选频率点的处理方法如下：根据前文模态试验结果，本文选取1.44 Hz，2.44 Hz，2.94 Hz，3.44 Hz，4.87 Hz，5.37 Hz，5.87 Hz，6.83 Hz，7.81 Hz，8.81 Hz，9.81 Hz，11.23 Hz，12.23 Hz，13.67 Hz，14.67 Hz，15.63 Hz，17.58 Hz，18.55 Hz，20.97 Hz，21.97 Hz，22.97 Hz以及23.93 Hz，作为灵敏度分析时的频率点。

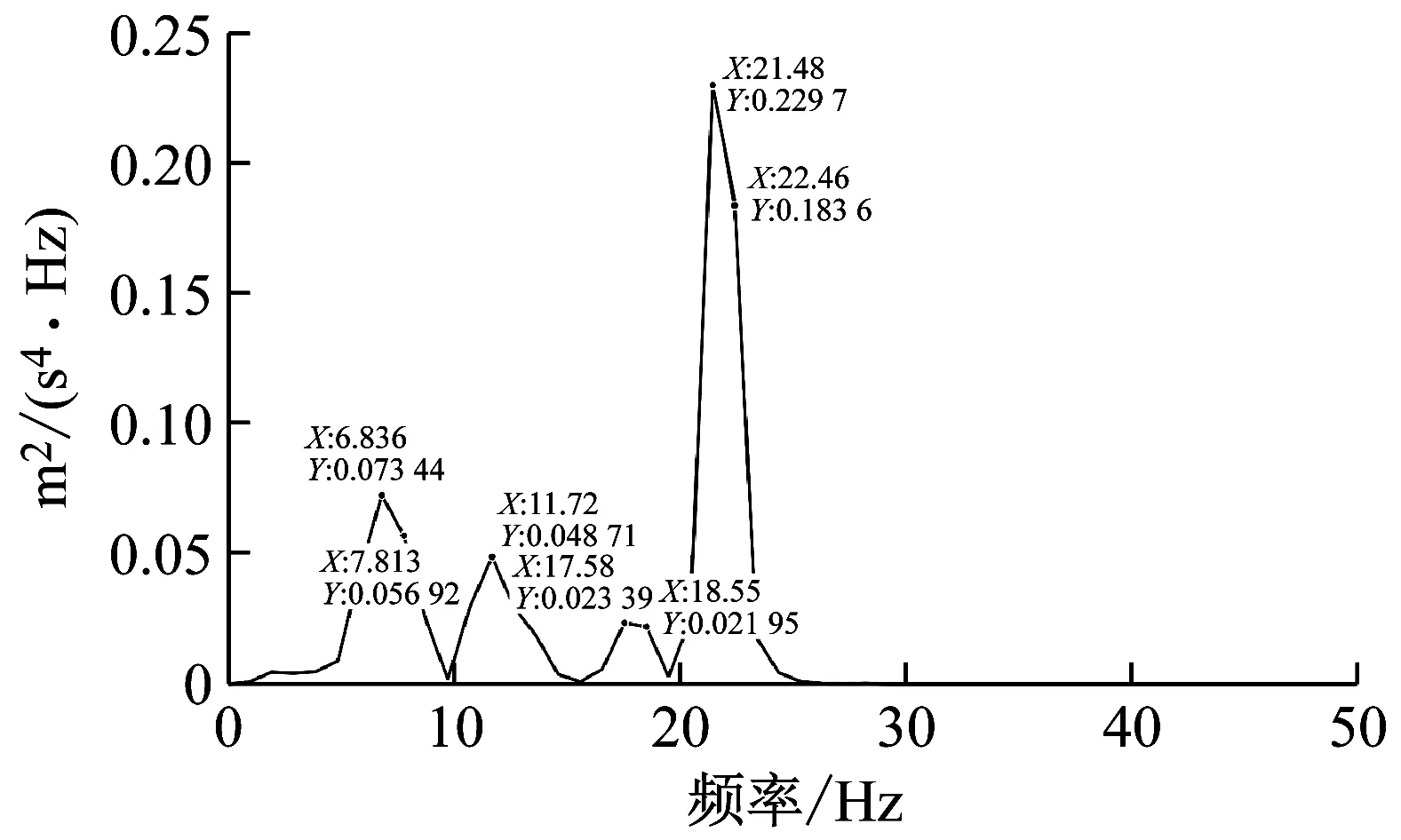
(a) 第2层测点加速度响应自功率谱密度

设各频率点幅值参数为1，将总时长分为45段，迭代收敛的条件μ=0.001。根据本章所提出的基于灵敏度分析的动载荷分段识别方法得到识别结果，平稳随机载荷时域样本识别结果以及相应的识别载荷功率谱密度如图6所示。

(a) 平稳随机载荷样本的时域识别结果

为了进一步定量分析本文提出的识别方法的有效性和准确性，定义两个指标作为评判随机信号识别结果好坏的标准，一个是识别载荷与真实载荷之间的均方根误差(mean square error，MSE)，MSE越小说明识别结果与真实值之间误差越小，两者越接近，另一个是识别载荷与真实载荷之间的相关系数R，R越接近于1说明识别结果与真实值的形状和变化规律越相似。

(17)

(18)

对于本试验算例，识别结果与真实载荷之间的MSE为4.03，R值为0.958 4，说明识别载荷能够较为准确地反映真实载荷的变化规律。从识别结果图中可以看出，在某些位置存在着识别结果不够光滑以及峰值识别误差较大的现象，这也是造成识别结果与真实载荷之间RMSE较大的原因。总体来看，本文提出的方法能够很好地识别出作用在8层框架结构上的各态历经的平稳随机动载荷样本。

5 结 论

本文针对时域随机动载荷，提出了一种基于灵敏度迭代分析的时域分段识别方法，将载荷时间历程进行分段并将每一小段内的载荷表示成正弦函数叠加的形式，通过灵敏度分析方法确定相关载荷参数得到其时间历程，整合各段结果从而得到平稳随机动载荷样本总体时间历程。在灵敏度分析中，针对迭代分析过程中的病态问题，采用了正则化处理方法。指出了在识别的每一小段载荷样本时，只需通过选定的频率点，对幅值进行灵敏度分析迭代来识别该时段内的平稳随机动载荷样本，并给出了频率点选取原则。讨论了相邻时间段之间的相互影响及处理方法。试验结果表明该方法能够很好地识别出作用在8层框架结构上的各态历经的平稳随机动载荷样本，是一种具有应用前景的时域动态载荷识别技术。