双向激励下非线性压电俘能系统的稳态响应分析

夏光辉, 康小方, 李 聪, 陈雷雨, 许庆虎, 满大伟

(1.安徽建筑大学 土木工程学院,合肥 230601；2.安徽建筑大学 安徽省BIM工程中心,合肥 230601；3.安徽建筑大学 安徽省装配式建筑研究院,合肥 230601)

随着物联网技术等为代表的高科技飞速发展，使得微机电系统和无线传感系统、射频识别、无线通讯、嵌入式系统等为代表的高新技术突飞猛进。越来越多的微型执行器、传感器不断涌现。为了给微电子器件提供自供电系统，采用压电振动能量俘获系统将环境中的动能转换成电能为微电子器件提供能源是一种切实可行的途径。近20年来，压电俘能技术被广泛研究和应用[1-2]。包括用于生物体运动的俘能技术[3]、建筑健康监测的分布式传感器节点[4]、用于医疗的嵌入式或植入式传感器节点[5]、汽车轮胎压力监测系统[6]、无人飞行器以及物联网智能家居系统[7-8]等。

在早期的数学建模中，大多数研究者都集中在使用振动俘能系统的线性模型[9-11]，同时研究者们也多使用了集总参数模型(单自由度模型)[12]。虽然集总参数模型通过简单的方法给出了对问题的初步理解，但是它只局限于单一振动模式，缺少物理耦合系统的振型信息，准确的应变分布以及它们对电学响应的影响等。为了从外界环境中俘获更多的振动能量，需要使压电俘能器件的工作频率接近环境振动频率，也就是让俘能器在接近共振的状态下工作。而在接近共振的状态下，俘能器件振动的幅度往往是比较大的。在这种振幅较大的情况下，俘能系统及其环境中的非线性因素将会对俘能器件的性能有明显影响，所以必须加以考虑。预测压电俘能器件在非线性共振现象发生时的工作状态，对于其设计非常重要，其非线性分析是非常有必要的[13]。Stanton等[14-15]对一悬臂梁双晶片压电俘能器进行模型数值理论计算以及实验分析，在几何线性和无端部质量块的情况下考虑了非线性压电材料的本构方程[16-17]。由于在相当低的基础加速度值的情况下非线性效应变得明显，研究结果得出，在共振点附近运行的压电俘能器的性能评估时有必要考虑材料非线性，包含适当非线性项的物理模型可以用来充分捕捉实验观察到的行为。Erturk等[18]对一个压电磁弹性结构的极限环振荡进行了非线性分析和实验，在一个相对宽的频率范围内，此结构产生了一个数量级较大的功率输出。Abdelkefi等[19]研究了考虑几何非线性和阻尼非线性的参数激励下的压电式俘能器模型。根据激励频率，得出对于二次非线性阻尼较小值的情况下，存在一个与亚临界分叉有关的跳跃。Daqaq等[20]对振动俘能的非线性研究进行了较为系统和全面的总结。Leadenham等[21]对双晶片悬臂梁压电俘能、传感和驱动进行了详细的理论分析和实验验证。由于上述的研究基本上都只是涉及单向激励状态，但是自然界中的振动源往往存在很多双向以及多向振动，所以对于混合振动的研究在近几年来引起了学者们的较高关注。Fang等[22]研究了悬臂式压电俘能系统在参数激励和外部直接激励下的俘能性能，采用单模Galerkin方法和谐波平衡法求出频率响应曲线的解析表达式，得出一些有意义的结论，但在他们的研究中未曾考虑非线性阻尼对压电俘能系统俘能性能的影响。Xia等[23-26]研究了参数激励和直接激励下悬臂梁压电俘能系统的非线性问题，得出大多数参数激励系统具有初始阈值，低于初始阈值，参数激励收敛到零稳态响应，没有能量可以俘获。对于参数激励系统，阻尼系数和负载电阻对参数激励下压电俘能系统的初始阈值影响较大。

基于基础激励的多向性和实际环境中的低频率环境，研究了参数激励和直接激励下附加端部质量块悬臂梁压电俘能系统的非线性问题。通过Hamilton原理对一个附加端部质量块悬臂梁双晶片压电俘能系统模型的非线性偏微分方程进行理论推导和计算分析。此压电俘能系统模型在固定基础端受到水平和垂直的双向激励，假设此悬臂梁为轴向不可伸长的Euler-Bernoulli梁，此模型主要包含几何非线性和阻尼非线性。利用Galerkin法将非线性偏微分方程降阶得到参数激励和直接激励作用下附加端部质量块悬臂式压电俘能系统的机电耦合运动微分方程。为了研究压电俘能系统在其主要的一阶共振情况下的响应，采用多尺度法获得了俘能系统的垂直位移、输出电压和输出功率的解析表达式。得到其主要一阶垂直位移幅值，输出电压幅值和输出功率幅值。分析了不同激励情况下，激励相位等对压电俘能系统俘能性能的影响。

1 俘能系统模型

1.1 几何模型

图1表示双向激励下压电俘能系统的模型图。梁由基层和上下两层压电层组合而成，假设压电层与基层紧密结合，基层与压电层之间的电极厚度可以忽略不计。梁的长度为L，宽度为b，厚度为hb=2tp+ts，ts为基层的厚度，tp为单层压电层的厚度。采用双晶串联方式与外载电阻RL相连接。M为端部的质量块质量，lM为质量块的水平长度，hM为质量块的纵向高度。

图1中oxy为惯性坐标系，o′x′y′为局部坐标系，悬臂梁固定端的水平位移为wx(t)，垂直位移为wy(t)。s为沿着梁中性面处的坐标，其在x′方向为u(s,t)，在y′方向为v(s,t)。

1.2 数学模型

根据文献[26]中的式(16)～(17)得到双向激励下压电俘能系统机电耦合的无量纲运动方程如下

(1)

(2)

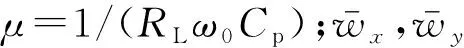
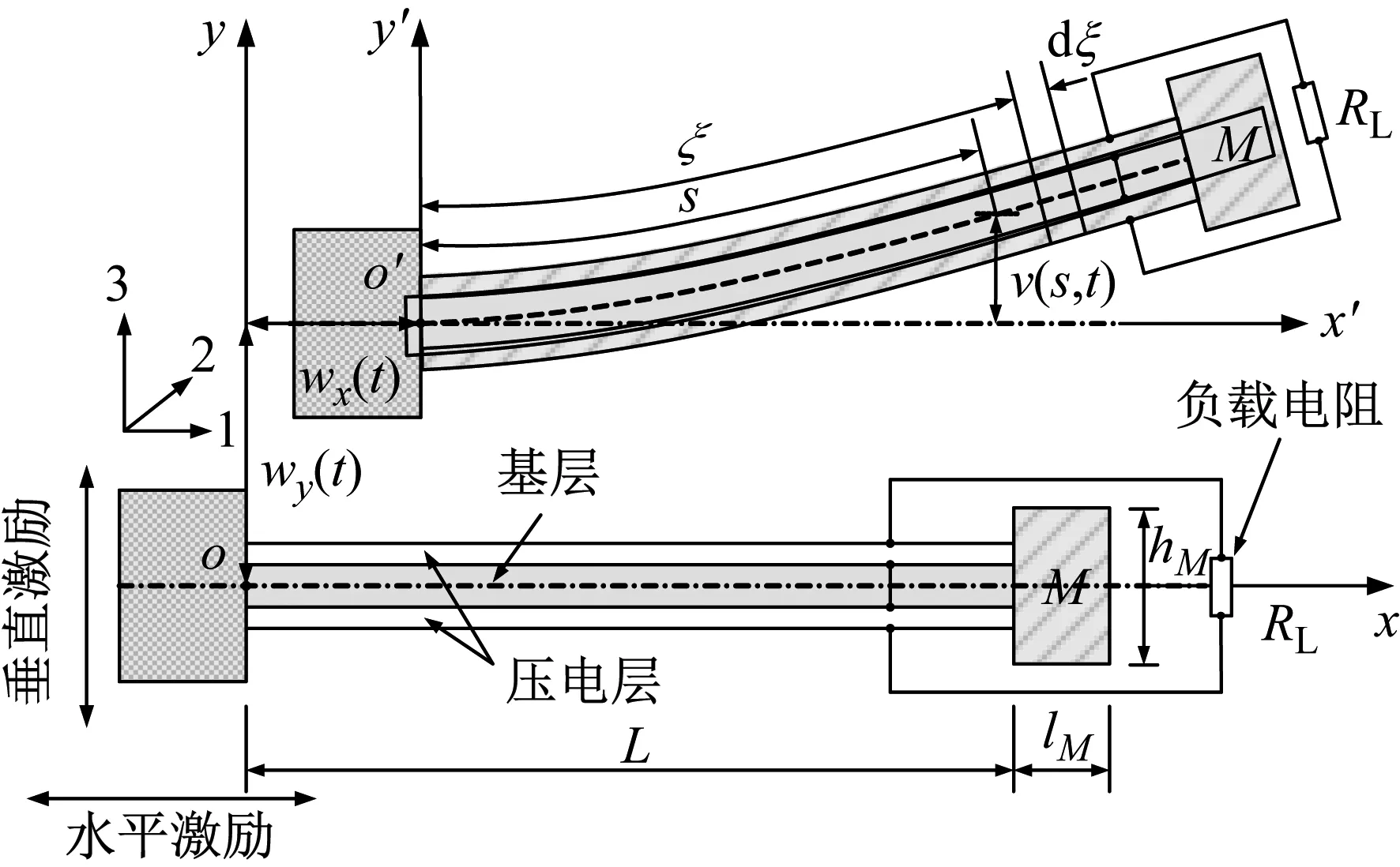
(a) 立面图

2 近似解析解

为了获得式(1)和(2)的解析解，首先利用Galerkin法将式(1)和(2)转化为一组非线性常微分方程，然后采用多尺度法获得机电耦合方程的解析解，研究压电俘能系统非线性特性并分析稳态响应的稳定性。

在参数激励和直接激励下附加端部质量块的悬臂式压电俘能器的非线性机电耦合降阶方程如下

(3)

(4)

其中：

(5)

(6)

我们采用多尺度法求解式(3)和(4)的解析解，假设取第一阶主振型，n=1，基底受到谐和激励为

(7)

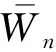
(8)

(9)

其中：

μ=μ0,ηn=η0,χn=χ0

(10)

(11)

消除永年项，即令exp(iΩ0T0)的系数为零，得：

(12)

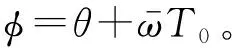
我们将复数A写成极坐标的形式

(13)

式中,a，θ都为时间T1的函数。

将式(13)代入式(12)，进行实部和虚部的分离得到：

c8asin(2φ)

c8acos(2φ)

(14)

式中,φ=σT1-θ。

c1a+cQa2+c2a3+c3a5+c4sin(φ+ψ)+c8asin(2φ)=0

(15)

式中,

(16)

式(14)的φ为相位变化，从-π≤φ≤π。由式(15)第一式求出a的值，然后将a以及相应的φ值代入式(15)第二式求出σ。将求出的a，σ及相应的φ值代入式(10)和(11)，即可获得无量纲位移响应和输出电压响应的解析表达式

(17)

(18)

式中,θ1=arctan(μ0/Ω0)。

稳态响应的输出功率响应的解析表达式为

(19)

对于稳态响应的非平凡解，为了确定非平凡解是否稳定，通过在定常点(a0，φ0)上引入一个时变的无穷小扰动(δa(t)，δφ(t))，即：a=a0+δa(t),φ=φ0+δφ(t)可以求出定常点的稳定性。我们考察式(14)，它的Jacobi矩阵为

(20)

其中，

k12=-c4cosφ0-2c8a0cos(2φ0)

k22=c4sinφ0/a0+2c8sin(2φ0)

(21)

Jacobi矩阵的特征方程如下

(22)

Δ1=-(k11+k22)>0

Δ2=-(k11+k22)(k11k22-k12k21)>0

(23)

3 结果分析

利用前面导出的解析解，本章主要研究双向激励下非线性压电俘能系统的稳态响应中相位的影响。文中所有图形实线部分表示稳定解，虚线部分表示不稳定解。ρM为质量块的密度，bM为质量块的水平宽度。梁的几何和材料参数为：

L=50 mm,b=20 mm,ts=0.2 mm,tp=0.2 mm,

m=96 g/m,Ys=20×109N/m2,Yp=60.9×109N/m2,

ρM=7 165 kg/m3,lM=5 mm,bM=20 mm,

3.1 单独参数激励和单独直接激励作用下相位的影响

当单独参数激励的时候，直接激励为零，即δy=0，此时c4=0，包含相位项的系数为零，相位变化对压电俘能系统无影响。

单独直接激励的时候，δx=0，从而c8=0。相位ψ变化对单独直接激励的稳态响应的位移幅值、输出电压幅值和输出功率幅值幅频响应曲线都没有影响。

3.2 参数激励和直接激励同时作用下相位的影响

为了研究相位变化对压电俘能系统的影响，分别研究了ψ变化的九种取值。

(a)

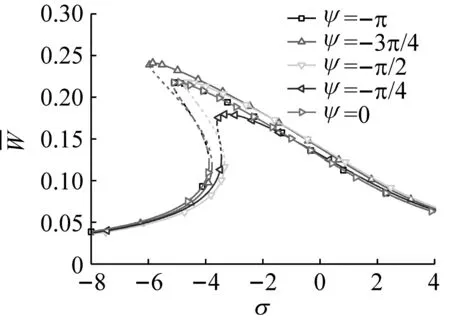
(a)

(a)

3.3 参数激励和直接激励同时作用下激励幅值的影响

(a)

4 结 论

对双向激励下考虑几何非线性和阻尼非线性的附加端部质量块悬臂梁压电俘能器数学模型进行理论推导，得出输出功率的解析解表达式。研究了激励相位和参数激励幅值变化对压电俘能系统性能的影响。具体结论如下：

(1) 单独参数激励或单独直接激励下，激励相位的变化对此压电俘能系统的稳态响应位移幅值、输出电压幅值和输出功率幅值都没有明显影响。

(2) 在同时参数激励和直接激励下，激励相位的变化对压电俘能系统的幅频响应有较大影响，双向激励下压电俘能系统的相位变化响应周期是π。合适的相位取值，可以使压电俘能系统的工作频带拓宽，提高压电俘能系统的俘能性能。

(3) 固定直接激励不变，选取合适的激励相位，参数激励幅值的增加，会显著加强非线性软化现象，并且使压电俘能系统的稳态响应进入到一个双峰状态，从而使压电俘能系统的俘能效率得到提高。