基于高斯过程回归的桥梁多变量地震易损性分析
2022-12-15闫业祥孙利民
闫业祥, 孙利民,2,3
(1.同济大学 桥梁工程系,上海 200092;2.同济大学 土木工程防灾国家重点实验室,上海 200092;3.上海期智研究院,上海 200232)
地震易损性分析表达了在给定地震动强度的条件下工程结构达到或超过某个性能极限状态的概率,已广泛应用于土木基础设施的震前风险预测、震后快速评估以及为抗震加固提供依据。在由太平洋地震工程研究中心发展的新一代基于性能的地震工程框架中,地震易损性分析是极其重要的一环,涵盖了需求分析与损伤分析两大模块[1]。地震易损性分析的一个重要结果是地震易损性曲线,定义为结构在不同的地震强度指标(intensity measure, IM)下对各性能极限状态的超越概率函数。但是,当前广泛使用的地震易损性曲线建立在单一的参数(即一个标量IM,譬如峰值地面加速度PGA,或结构第一阶周期处的谱加速度)之上,其不足主要体现在两个方面:① 单一的IM不足以表征地震动对结构的破坏能力,而矢量IM可能更有效[2];② 结构相关参数中存在的不确定性对易损性有不可小觑的影响[3]。因此,传统的基于单参数的地震易损性曲线无法弥补上述不足,亟需一个新的工具来考虑多重变量对易损性的影响,这正是本文发展多变量地震易损性分析方法的背景与目的。
当前已有一些学者对多变量地震易损性分析作了有益的探索[4-6],其中基于代理模型的Logistic回归是一种较为有效的方法。该方法主要利用代理模型(也称元模型或近似模型,譬如响应面模型、神经网络回归等)来代替有限元“黑箱”分析,通过代理模型预测的大样本地震需求来构造生存-失效二值矢量(0代表安全,1代表超越了极限状态),并在此基础上拟合Logistic回归获得构件的多变量地震易损性函数。上述方法的主要缺点在于流程上的繁琐以及单一的IM仍被使用,而且易损性函数的精度极大地依赖于代理模型的预测精度以及Logistic回归的拟合精度。不同于上述方法,本文提议了一个新的基于地震需求均值和需求方差模型的多变量地震易损性分析方法,并可以直接包含矢量IM与多重结构参数。其中均值与方差采用高斯过程回归来拟合,高斯过程回归是一个非参数机器学习方法,最近一些研究已将其应用于结构的抗震性能评估中[7-9]。作为多变量易损性函数的直接扩展,本文发展了均值与包络易损性曲线的概念以充分考虑各种不确定参数的影响。最后,识别了不同的IM对易损性曲线离散性的影响,并确定了最优的IM形式。
1 基于高斯过程回归的多变量地震易损性模型
1.1 多变量概率地震需求模型
当前的地震易损性评估方法主要采用非线性动力分析进行,即在一系列结构参数与地震动时程的随机组合下进行弹塑性动力分析,然后基于结构地震需求(或损伤指标)和输入参数进行后续的易损性分析。当采用多元回归的方式构造地震需求与输入参数之间的数学关系时,可建立如下表达式
lnyD=g(lnX)+ε
(1)
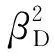
式(1)实质上是使用回归模型来代理隐式的非线性有限元模型,它将地震需求分为了两部分:均值部分与误差部分。均值部分呈现了对平均地震需求的预测;而误差部分则主要来源于如下两个方面:① 有限的IM难以全面呈现地震动之间的变异性;② 回归模型本身的拟合能力难以完全代替真实的有限元模型。因此,本文建议对均值与误差分别建立回归模型来预测结构的地震需求
mD=gm(X)
(2)
(3)
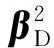
r2=(yD-gm(X))2
(4)
当然,一个常数方差估计也可利用下式得到
(5)
比较式(3)和式(5)不难发现,常数方差仅仅平均了残差平方,而式(3)则是一个更加灵活的回归模型,可以捕捉到可能存在的异方差模式,即方差随着输入参数的变化而出现一定的趋势。
1.2 高斯过程回归
式(1)提供了一个多变量需求模型的框架,其中回归模型可以是任意的。本文使用高斯过程回归作为特定的代理模型考虑到其强大的非线性拟合能力以及灵活的超参数求解技术。
所谓的高斯过程回归即是假定地震需求在所有的N组样本上服从一个均值矢量为mN和协方差矩阵为CN的高斯过程先验
yD~GP(mN,CN)
(6)
在实际使用时,mN可以设置为零元素矢量(即响应数据减去其均值),而协方差矩阵CN∈RN×N中的每个元素可以表达为
(7)
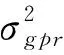
(8)
(9)
式中,κ*为核函数矢量,具有如下形式
(10)
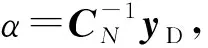
(11)
结合式 (9)~(11) 可以看出在新样本上的预测即为利用既有的N组地震响应样本进行加权求和,距离新样本点越近,则对预测的贡献越大。
1.3 多变量地震易损性函数
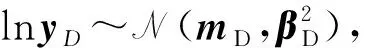
(12)
式中:X*是由x*按行组成的矩阵;K*则是κ*按行构造的矩阵;下标m和β分别用来指代均值与方差的高斯过程回归预测。式(12)之所以是多参数的,是因为新的样本点中可以包括任意的IM和结构参数矢量。之所以称作易损性函数,是因为IM可以设置为逐渐增加的形式。
式(12)可直接用于桥梁构件层次的易损性模型,此时每个构件对应一个地震需求矢量yD。为了获得一个参数化的系统层次易损性函数,本文提议一个基于多元高斯Copula函数的方法。首先根据结构可靠度理论,多重构件的串联系统的易损性函数[11]可以表示为
(13)
式中:m为构件的数目;Fi,Fj,…Fm分别为各构件的易损性函数;P(FiFj…Fm)为所有构件之间的联合易损性函数,其余项类似。式(13)的关键点在于联合易损性函数的求解,用高斯Copula函数可以近似的代替为
P(FiFj…Fm)=CGauss(F)=
ΦR(Φ-1(F1),…,Φ-1(Fm))
(14)
式中:CGauss(·)为高斯Copula函数;ΦR(·)为协方差矩阵等于其相关系数矩阵R的多元高斯累计分布函数;Φ-1(·)为单变量标准正态分布的逆累积分布函数。式(14)的前提假定是将各构件的易损性函数看作某个变量的累积分布函数,这与经典易损性模型中的假定是一致的[12]。将式(12)和式(14)代入式(13),即可获得系统层次的易损性函数,且保留了多变量和参数化的特性。应当注意本文仅分析了基于高斯Copula函数的串联系统多元易损性模型,至于其他的系统形式(如并联和混合串并联等),可直接扩展式(13);对于其他Copula函数类型(如Clayton、Frank、Gumbel等形式),可直接扩展式(14)。更多的发现将有赖于详细的比较研究,限于篇幅本文暂未考虑。
1.4 均值与包络易损性曲线
将任意给定的参数组合代入式(12)~(14)即可获得一个特定极限状态的超越概率,因此在连续变化的参数组合下其表现为高维空间中的易损性曲面。为了对应经典的单变量易损性曲线,可通过下式的高维积分得到
Fm(im)=FIM1[FIM(X)]=
(15)
式中:EIM1[·]为向标量IM1求取期望的算子;IM*为除去IM1以外的地震强度指标;fΘ和fIM*分别为结构参数Θ与IM*的联合概率密度函数。可见式(15)为一个以积分求期望的过程(先积分结构参数再积分强度指标),但是当变量维度很高或者变量间有相关性时变得十分复杂,甚至不可解。因此本文提议使用如下的非线性曲线拟合方式以获得易损性曲线
(16)
图1显示了式(16)的拟合过程,首先将易损性投影到F-IM1平面内,然后通过非线性最小二乘拟合出一个参数为λim和βim的对数正态分布的累积分布函数。式(16)所求的易损性曲线实质上是考虑了所有参数随机性的一个平均,因此将其称作均值易损性曲线。
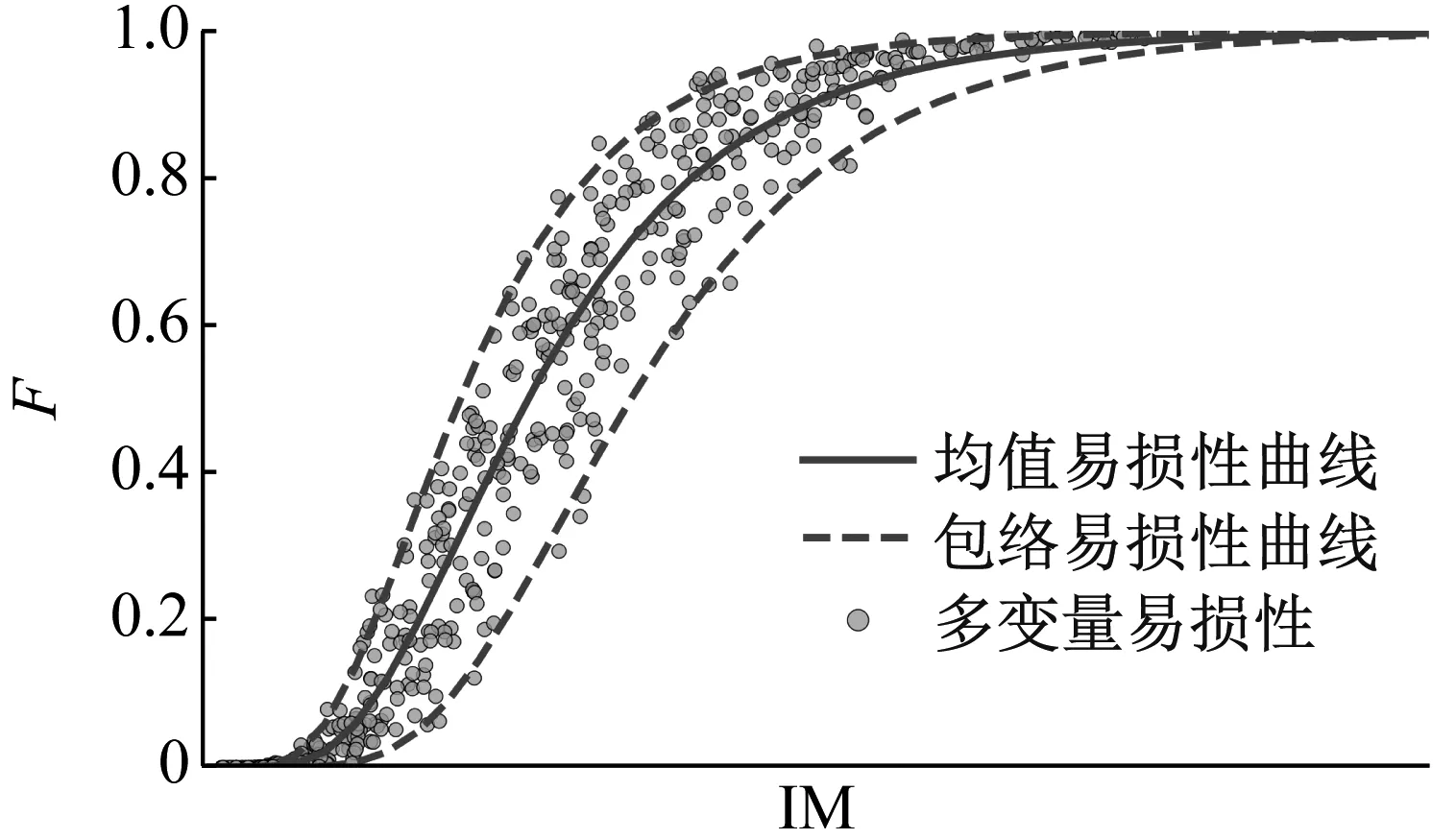
图1 均值易损性曲线与包络易损性曲线
既然投影到F-IM1平面内的易损性是离散的,且式(16)代表了其均值,那么其包络易损性曲线也可以容易获得。首先提取出离散易损性点的包络点,对上界和下界包络点分别应用式(16)即可获得包络易损性曲线,如图1所示。
2 多变量地震易损性分析步骤
本文提议的多变量地震易损性分析的具体步骤,如图2所示。
步骤1:选择数量为N0的地面运动记录,对于具有两个正交水平分量的记录可取其几何均值作为新的记录。确定用来缩放地面运动的地震强度指标IMs(譬如PGA或Sa(T1))以及缩放目标区间[IMsmin,IMsmax]。
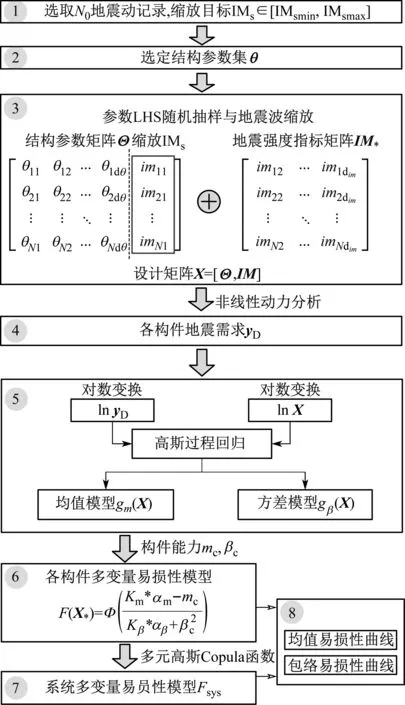
图2 多变量地震易损性分析流程图
步骤2:选定随机结构参数Θ。
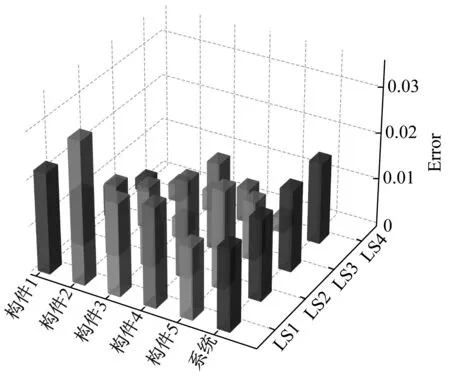
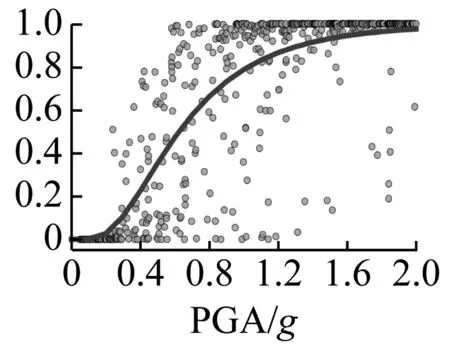
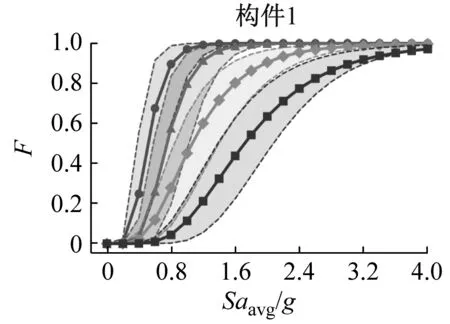
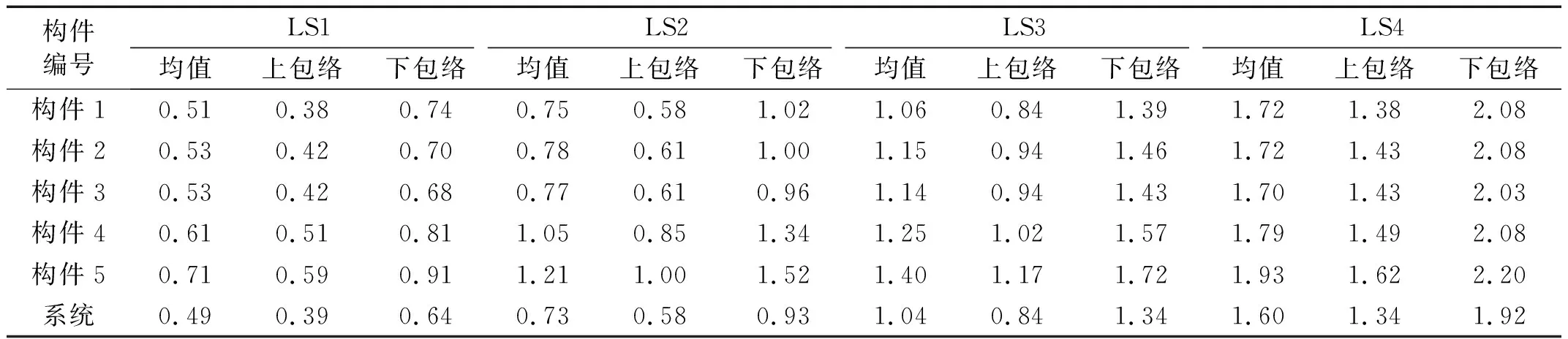
步骤3:利用拉丁超立方抽样(LHS)技术抽取行数为N的结构参数矩阵。注意将上述IMs设置成[IMsmin,IMsmax]内的均匀分布,和结构参数一起进行抽样。并以生成的IMs样本为目标对N0条地震波进行缩放。如N0 步骤4:利用生成的N个结构参数组合与N条缩放后的地震波代入到有限元模型进行非线性动力分析,得到每个构件的地震需求矢量yD。 步骤5:将yD和X进行对数变换后进行高斯过程回归,分别建立均值需求模型和方差需求模型。 步骤7:假定系统为串联,利用高斯Copula函数建立系统的多变量地震易损性模型Fsys(X*)。 步骤8:分别拟合构件与系统层次的均值易损性曲线与包络易损性曲线。 需要强调的是步骤3中将缩放目标IMs与结构参数一起进行拉丁超立方抽样的目的是使生成的结构参数样本和目标IM保持空间填充特征,这类似于增量动力分析(IDA),区别在于IDA的缩放IM是离散的,而本文是在区间[IMsmin,IMsmax]内均匀连续分布的。因此,这种均匀缩放的方法能够以尽量少的动力分析次数获得尽可能高的易损性精度,而这也得到了后文的蒙特卡罗方法的验证。 本文的算例为一座60 m+100 m+60 m三跨钢筋混凝土连续梁桥,采用单柱式桥墩,两墩等高16 m,空心矩形截面,尺寸为纵桥向3 m,横桥向8 m,壁厚0.8 m。上部结构为变截面连续箱梁,宽17 m,高3 m。支座为盆式橡胶支座。由于本文目的是发展易损性分析方法,为简化问题忽略了基础对桥梁动力响应的贡献。利用地震工程仿真平台OpenSees建立了如图3所示的桥梁有限元模型。上部结构采用弹性梁单元模拟;桥墩采用基于力的纤维截面梁柱单元模拟,其中混凝土纤维的本构采用Concrete01材料模拟,核心区混凝土采用Mander模型来计算箍筋的约束效应,钢筋纤维采用Steel01材料模拟。桥台与填土之间的被动力-位移关系使用Hyperbolic Gap材料模型,桥台与主梁之间的冲击则利用Impact材料模拟。对于可滑动支座,使用理想弹塑性模型来模拟其摩擦作用。图3(b)列举了这些本构模型的参数,其具体解释请参照OpenSees的用户手册,关于参数的计算方法可参见文献[13]。利用该有限元模型,并将第3.2节中的随机参数设置为其均值,可以计算出桥梁的动力特征。由计算得桥梁的前两阶模态周期分别为0.71 s和0.42 s,其振型均包含桥墩的纵向弯曲。因此为节省篇幅,本文仅分析纵桥向上的易损性,并利用这两阶振型的频率计算Rayleigh阻尼矩阵的质量和刚度比例系数,用于随后的动力计算。 (a) 桥梁有限元模型 既然式(12)所示的易损性函数可以包含多个变量,因此可以将桥梁参数设置为随机变量以考虑其不确定性对易损性的影响。本文共选取21个与桥梁地震响应有关的随机参数,如表1所示。这些参数包括4个无约束混凝土本构参数(fcc-峰值受压强度,εcc-与峰值强度对应的应变,fcu-极限受压强度,εcu-极限受压应变);1个与所有混凝土构件相关的参数ρc-混凝土质量密度;4个受约束混凝土的本构参数,其参数符号意义与无约束下的相同;3个与钢筋本构相关的参数(fys-屈服应力,Es-弹性模量,bs-屈服后刚度比);3个与支座摩擦有关的参数(Fy1-桥墩上支座的屈服力,Fy2-桥台上支座的屈服力,δy-屈服位移);3个与桥台-主梁冲击有关的参数(K1-初始刚度,K2-二次刚度,xy-屈服位移);2个与桥台-填土被动挤压有关的参数(Kmax-初始刚度,Fult-极限被动土压力);1个桥梁阻尼比参数。 表1 各随机结构参数的概率分布特征 本文共对五个构件进行易损性分析,包括桥台后回填土,桥台上支座以及墩上支座,纵向固定支座下的桥墩墩底和墩顶截面。桥台和回填土之间的峰值压缩位移,支座的纵向峰值滑动位移以及桥墩截面的曲率Park-Ang指标分别作为其损伤测度。曲率形式的Park-Ang指标定义如下 (17) 式中:φy和φu分别为等效屈服和极限曲率,My为等效屈服弯矩,上述参数可由截面的弯矩-曲率分析得到;φm是地震产生的截面峰值曲率;ET是由滞回耗散的能量;因子βPA用来呈现循环荷载对结构损伤的影响,本文取为0.294。 共定义轻微、中等、严重和完全破坏四种极限状态(limit states, LS),每个构件的每种极限状态所对应的能力概率分布如表2所示。所有构件的抗力被假定为对数正态分布,并为轻微和中等破坏采用较低的变异系数0.25,而为严重和完全破坏状态指定更高的变异系数0.5,关于确定分布参数的细节参见文献[12-14]。 表2 各构件极限状态与能力的均值 本文选取了报告FEMA P695[15]中整理的50条地震动记录,包括22条远场记录,14条近场无脉冲记录,以及14条近场含脉冲记录。这50条地震波将根据第2章中的设计样本总数N进行缩放。譬如N=500,则先将50条地震波复制10次,然后根据拉丁超立方抽样生成的500个IMs样本进行缩放,这样既保证了地震波的随机缩放特征,又保证了和结构参数一起的空间填充特征,因此共进行N次非线性动力分析。关于地震波的细节参见FEMA P695,本文不再列出。 对于本文,考虑到PGA更加容易缩放,将其作为缩放IMs并在[0,2g]内采样。为了充分考虑到其余IM对易损性精度的贡献,本文增加了另外3种地震动强度指标,分别为峰值地面加速度PGV,结构第一阶自振周期处的谱加速度Sa(T1),以及周期区间[0.2T1,2T1]内的几何平均谱加速度Saavg。为了呈现缩放后的地震波的上述IM的分布特征,图4显示了N=500时各IM的分布,其中PGA服从[0,2g]内的均匀分布,这正是本文所采用的均匀缩放所期望的结果,而其余三个IM拟合成了对数正态分布。对于算例桥梁T1=0.71 s,Sa(T1)与Saavg的均值分别为1.57和1.19g,而PGV与结构无关,均值为1.44 m/s。 按照第2章中的流程即可获得各构件的地震需求矢量yD与输入参数矩阵X,对数变换后应用高斯过程回归即可获得结构的地震需求均值与方差模型。图5显示了构件1和构件5的地震需求以及残差平方与PGA的关系,可以看出即使经过了对数变换地震需求与PGA之间的关系仍然呈现出了非线性,意味着传统的线性回归是不适用的,而高斯过程回归则可以较好地捕捉到非线性模式。此外,构件5的残差明显表现出了异方差模式,即随着PGA的增加方差逐渐增大。若使用常数方差估计,显然会在较高的PGA处低估其方差,而再次使用高斯过程回归进行方差预测则可以灵活地适应方差的变化。另外需要强调的是构件1的异方差模式不显著,则高斯过程回归直接给出了常数方差估计,即如果从残差中学习不到任何模式,其最终会给出一个均值估计。因此,高斯过程回归可以灵活地适应任何方差模式,这也是本文发展需求方差模型的原因。其余构件与此类似,不再赘述。 实际上,样本尺寸会影响高斯过程回归的预测性能,进而影响到由此生成的多变量易损性函数的精度。为了研究其影响以及验证所提方法的精度,使用蒙特卡洛仿真来直接生成各构件的易损性。具体做法为将PGA在区间内分成以0.1g为增量的20个离散的水平,在每一个PGA水平利用第2节中的抽样技术抽取5 000个样本进行非线性动力分析,各极限状态下的超越概率可利用失效的样本数直接除以总数(即5 000)得到。因此基于蒙特卡洛的易损性总共实施了10万次动力分析。为了测量所提方法生成的均值易损性曲线与蒙特卡洛之间的误差,定义如下的指标 (18) 式中:Fi为所提议方法生成的均值易损性曲线在每个PGA水平处的值,Fmc,i则对应蒙特卡洛计算的失效概率,因此指标Error测量了二者在所有PGA水平上的平均易损性偏差。 图6为各构件与系统层次的易损性误差随样本尺寸N的变化情况,在N=50时所有构件和系统有较大的误差,这意味着较少数量的样本无法为高斯过程回归提供充足的训练。但是当N=100时易损性误差迅速减小,在N=300趋于稳定,即不再随着N的不断增加而减小。事实上,这些不能被缩减的误差是模型误差,来源于高斯过程回归的预测,以及在生成易损性函数时的正态性假定。若想继续减小这些误差,需要发展更加合理的代理模型以及易损性生成方法。 图6 易损性精度与样本尺寸的关系 对于本文算例来说,N=300可以认为是一个最优的样本尺寸,即在保证精度的同时最大程度地降低有限元分析的代价。图7显示了N=300时所有构件与极限状态的误差,这些误差都在0.02以下,这对于地震作用下的高失效概率来说是可接受的。此外,观察到系统层次的易损性误差也是较低的,表明本文所提议的基于多元高斯Copula函数的系统易损性函数生成方法是可靠的。至于本文所提议方法的效率,由于蒙特卡洛法的总分析次数为10万,因此效率比为300/(1×105)=0.003,可见本文所提议的方法具有非常高的计算效率。 图7 N=300时各构件与系统的易损性误差分布 4.2节验证了所提议方法的精度与效率,即生成的均值易损性曲线收敛于蒙特卡洛的解,不过使用的是PGA,使用PGA的原因是其作为缩放IM。但是其他的IM也可以用来生成均值易损性曲线,图8显示了由不同IM生成的均值易损性曲线的结果,每个IM的区间由图4推断得到。可以看出各图最大的区别在于易损性投影点的离散性,其中Saavg的最小,其次Sa(T1)和PGV,离散性最大的是PGA。越高的离散性说明还有更重要的参数影响着易损性,而其本身的影响则相对较小。因此,Saavg是一个更好的测度用来生成均值易损性曲线。尽管这样,Saavg仍具有一定的离散性,说明其它参数(包括其余IM以及结构参数)的影响也是不可忽略的,这也意味着任何单个参数都不足以完全呈现易损性,佐证了本文发展多变量易损性函数的必要性。此外,需要强调的是尽管PGA的离散程度较大,但是上节证明了其均值易损性曲线是精确的,因为其平均了所有不确定参数的影响,而离散性反映的是其不确定程度,可以由包络易损性曲线来呈现。 根据4.3节的分析,图9显示了所有构件以及系统层次以Saavg生成的均值与包络易损性曲线。由图可知几乎所有构件的所有极限状态的均值易损性最终都达到了1,而且包络易损性曲线的面积也几乎缩减至0,意味着失效是必然的,没有任何不确定性存在。这里Saavg的区间设置为[0,4g],这由图4中的均值和方差推断而来,即μ+3σ=1.19+3×0.88=3.83g,这说明虽然用来缩放的PGA限制在[0,2g]内,但是Saavg却可以高达4g左右,对于本文算例来说是很高的地震强度。此外,上下包络易损性之间的距离衡量了该极限状态易损性的不确定性程度,可以发现这种不确定性呈现了两端小(端部为0),中间大的特点,而且不同的极限状态之间会出现重叠现象,暗示着易损性曲线表征破坏状态之间的模糊现象,需要未来更深入地探索。 表3列出了所有均值与包络易损性曲线的中位值,即当超越概率为0.5时所需的Saavg强度,其值越小表明更加易损。表3显示桥台填土和支座比桥墩更加容易遭受地震损伤;由于固定支座下桥墩与上部结构表现为刚架形式,故而上端截面也承受较高的损伤概率,但稍低于底部截面;由于本文假定桥梁系统为串联形式,所以其中位值Saavg低于所有构件。 表3 均值与包络易损性曲线的中位值 最后需要强调虽然Saavg被建议用来拟合均值与包络易损性曲线,但是其依赖于结构的自振周期,因此PGA等与结构无关的指标仍然被建议用来缩放地震波,考虑到缩放与生成均值、包络易损性曲线是相互独立的环节。 本文提议了一个基于高斯过程回归的多变量地震易损性分析框架,可以将易损性表达为由地震动强度指标和结构参数组成的矢量输入的多元函数。生成的均值与包络易损性曲线能够全面考虑地震波与结构参数中的不确定性。以一座三跨钢筋混凝土连续箱梁桥为算例,结果表明本文所提议的方法与直接蒙特卡洛仿真具有相一致的精度,并且具有极高的效率,大大减少了有限元分析数量。通过比较研究发现,平均谱加速度Saavg是一个生成均值与包络易损性曲线更加合适的指标,考虑到其具有最小的易损性离差,而且在区间端部不确定性缩减为零。此外,研究结果显示任何单个参数均不能完全呈现结构的易损性,需要在分析中包含多重变量的影响。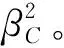
3 桥梁结构与有限元模型
3.1 有限元模型与本构关系

3.2 随机参数
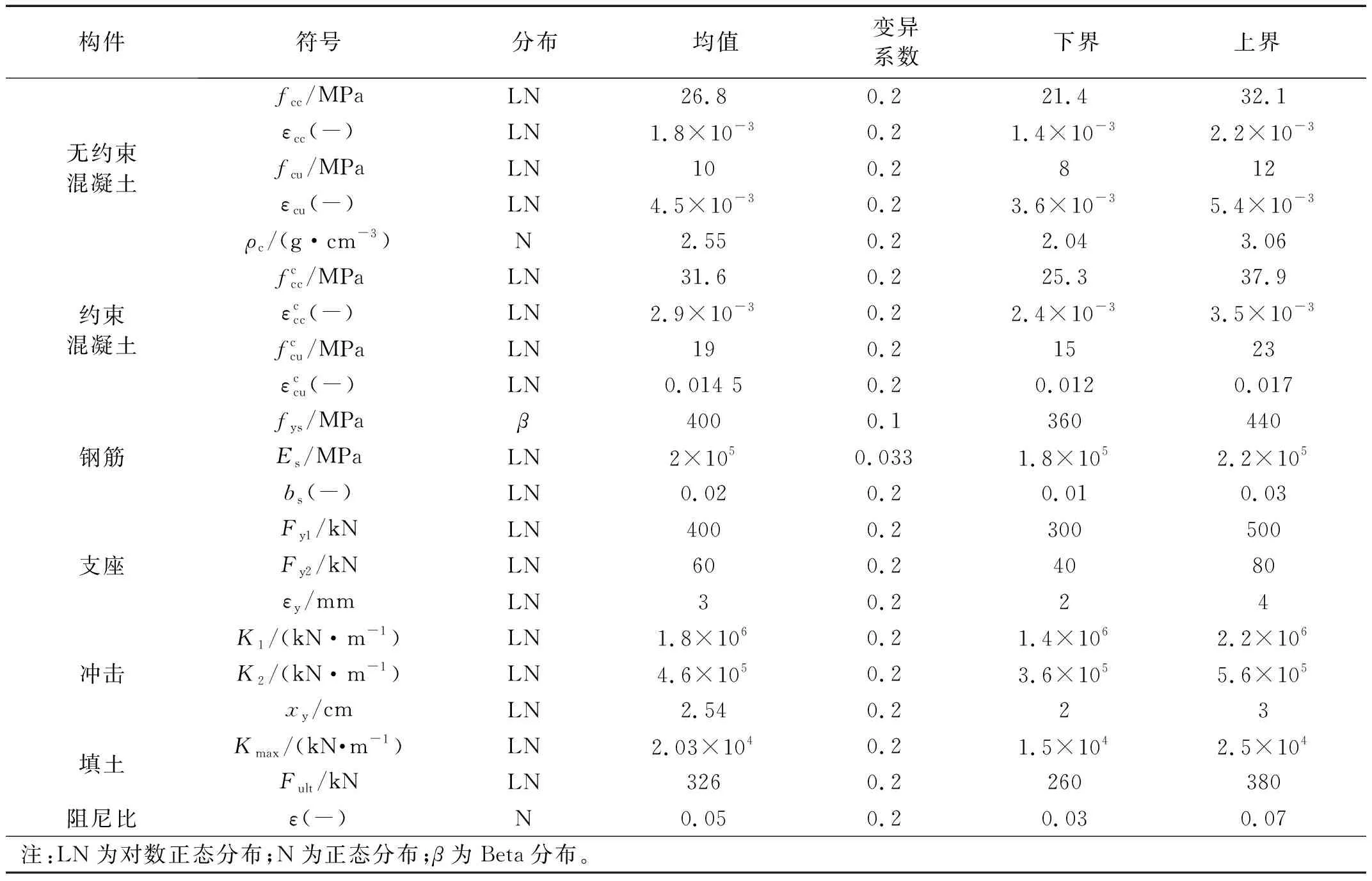
3.3 构件的损伤指标与极限状态
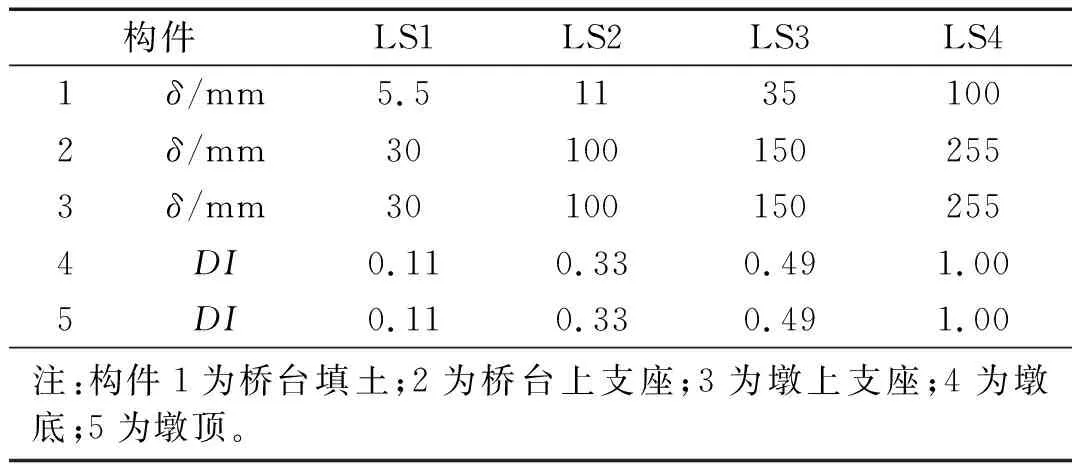
3.4 地震动记录
4 分析结果
4.1 地震需求均值与方差模型

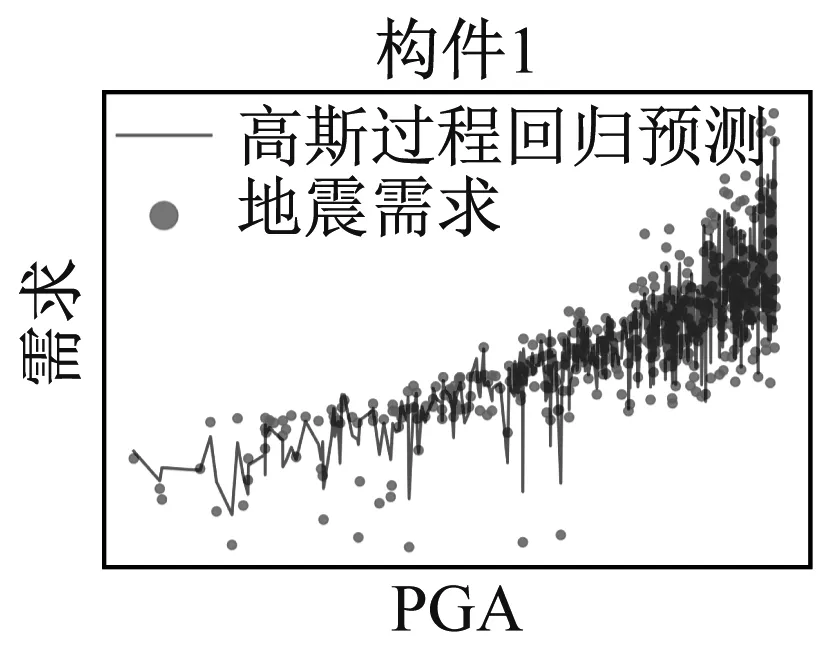
4.2 样本尺寸与模型精度验证

4.3 IM的影响
4.4 均值和包络易损性曲线
5 结 论
