中国经济增长对碳排放的非线性影响分析——基于PSTR的实证研究

张 省，王金营

（1.华北电力大学（保定），河北 保定 071003；2.河北大学 经济学院，河北 保定 071002）

一、引言

随着全球气候问题的日益凸显，碳减排问题成为世界各国面临的共同挑战。2020年习近平主席在第75届联合国大会中提出了“2030碳达峰，2060碳中和”的双碳目标。与此同时，作为全球第一大发展中国家，中国的经济发展水平与发达国家仍存在较大的差距，实现经济高质量发展仍为第一要务。十九大做出了“两步走”战略部署，即“到二〇三五年基本实现社会主义现代化；从二〇三五年到本世纪中叶把中国建成富强民主文明和谐美丽的社会主义现代化强国”。双碳目标与“两步走”经济增长目标是否会相互掣肘、彼此制约？两类目标能否同时实现？经济增长是否必然带来碳排放量的增加？回答这些问题，对中国经济增长对碳排放的影响进行深入分析就十分必要。

Grossman等最早对经济增长与碳排放的关系进行研究，并提出了EKC（环境质量与人均收入间的关系）倒“U”型假说[1]。然而，EKC假说在学术界一直存在着争议，国内外学者采用了不同的数据和计量方法对其进行检验，研究结论并不一致甚至截然相反，大致可分为三类：其一，EKC曲线表现为倒“U”型。国外学者Nasir等的研究证明了EKC倒“U”型曲线的存在[2]。在国内，王菲等(2018)发现中国整体及分区域均存在EKC倒“U”型曲线[3]。其二，EKC曲线表现为其他形态。席艳玲、牛桂敏(2021)[4]的研究证实了经济增长和碳排放之间“N”型曲线的存在；许华、王莹(2021)认为碳排放与经济增长呈倒“N”型曲线关系[5]；肖严华等(2021)发现经济增长与环境污染之间为正“U”型空间关系[6]，与Grossman的EKC假说恰好相反。此外，Mujtaba等(2020)认为经济增长和碳排放之间为负相关关系，李在军等(2022)认为二者为正相关关系[7]，而邓晓兰等(2014)认为两者之间呈单调递增关系[8]。其三，在不同的情形下EKC表现为不同的形态。如Galeotti等(2006)认为OECD国家的EKC呈倒“U”型关系，而非OECD国家为单调关系。林伯强、江竺均(2009)的研究发现ECK假说仅适用于经济发展水平较高的发达国家，发展中国家是否存在EKC倒“U”型曲线因情况而异。朱磊、张建清(2017)发现中国只有东部和东北部地区满足EKC假说，中部和西部并不满足EKC假说[9]。李国志(2018)则发现中国在1970—1989年间不存在EKC曲线，而1990—2015年则存在典型的倒“U”型EKC曲线[10]。

通过文献梳理可以发现如下问题：第一，很多EKC研究文献，大多采用时间序列模型、面板数据模型抑或空间计量模型，这种先验的形式在本质上都属于线性设定，应用线性形式的模型来检验经济增长与碳排放的非线性关系，欠缺合理性。文章拟应用面板平滑转换回归模型(Panel Smooth Transition Regression,PSTR)，研究经济增长对碳排放的非线性影响。第二，现有研究大多局限在经济增长对碳排放的影响是促进还是抑制。文章将突破这种单一的研究视角，关注影响系数的数值大小变化趋势，设置不同转换变量，从“门槛”效应的角度分析经济增长对碳排放影响发生变化的边界，深入研究经济发展水平、能源结构、技术进步、城镇化水平等不同省际特征差异对两者关系所产生的非线性影响。

二、研究方法与数据来源

1.研究方法

为研究不同经济发展水平、能源结构等地区差异下中国经济增长对碳排放的非线性影响，文章采用González等(2005)提出的面板平滑转换回归模型进行实证分析。PSTR模型基本形式为：

其中，i=1，2，…，N代表不同个体，t=1，2，…，T代表不同时间段。yit为被解释变量；xit为解释变量；ui和εit分别为个体的固定效应和随机扰动项。β0代表解释变量线性部分的系数，βj×Gj代表其非线性部分的系数。qit为模型的转换变量；Gj为转换函数，是关于转换变量qit的连续、有界函数，转换函数的值被标准化在0～1之间。r表示转换函数的个数。γ＞0代表斜率系数，决定模型转换发生的速度，其数值越大，代表转换速度越大。c=(c1，c2，…，cm)为m维位置参数向量，也称为门槛值，代表了模型转换发生的位置。转换函数Gj一般用Logistic函数的形式表示，如下所示：

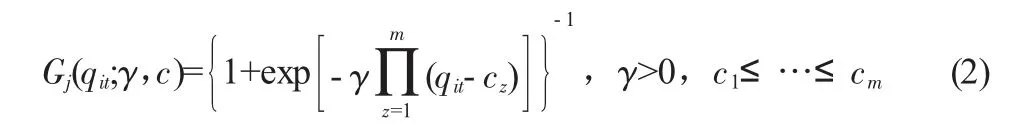
由于Gj是连续函数，当Gj在[0，1]区间内发生连续变化时，回归系数将在区间内完成连续平稳转化。m表示位置参数的个数，González等(2005)认为m取1或2足以具有代表性。此外，当转换变量qit为解释变量xit时，根据转换函数Gj的性质，式(1)中将包含解释变量xit的r+1次多项式，当有β0＞0且β0+β1＜0成立时，表明EKC曲线存在。

在PSTR模型中，xit对yit的影响系数与转换变量qit相关，yit关于xit的边际效应为：

2.变量选取与数据来源

文章选取1997—2019年中国30个省份（因数据缺失剔除西藏和港澳台地区）作为研究对象，样本数据来源于中国碳核算数据库、《中国统计年鉴》《中国人口统计年鉴》《中国能源统计年鉴》。变量的指标选取如下：

一是被解释变量：人均碳排放。目前大部分文献采用碳排放总量这一指标，考虑到影响碳排放总量的因素既包括经济因素，也包括人口因素，文章重点研究经济增长对碳排放的影响，有必要将人口因素对碳排放的影响排除在外。因此，文章选取人均碳排放量作为PSTR模型的被解释变量。

二是解释变量：人均GDP。考虑到中国人均可支配收入自2013年起统计方法和口径发生变化，文章选取人均GDP作为经济增长的表征指标。为剔除价格因素影响，以1997年为基期，计算得到各省不变价GDP，作为PSTR模型的解释变量。

三是转换变量。文章分别选取第三产业比重、城镇化率、煤炭消费比重、专利授权量、对外开放度分别作为模型1～5的转换变量，选取人均GDP同时作为模型6的解释变量和转换变量。PSTR模型中将包含人均GDP的r+1次多项式，根据各阶人均GDP回归系数的显著性和数值的正负，验证中国EKC曲线的具体形态。

三、结果分析

1.平稳性检验

为防止出现伪回归现象，文章首先采用面板单位根检验方法对各个变量进行数据平稳性检验。检验结果显示，文章所涉及的7个变量均在1%的显著性水平下平稳，可以进行建模。

2.线性检验

在使用PSTR模型进行估计之前，首先要进行线性检验（原假设H0：r=0，备择假设H1：r=1），检验在不同转换变量的影响下经济增长对碳排放是否存在非线性影响。根据线性检验结果，6个模型的LM、LMF、LRT三个统计量的P值均为0，即在1%的水平下均显著拒绝了原假设H0：r=0，说明经济增长对碳排放存在显著的非线性影响，文章建模具有合理性。

3.剩余非线性检验

剩余非线性检验的目的是确定PSTR模型中转换函数的最优个数r。若接受原假设H0：r=1，则认为模型只设定一个转换函数是恰当的；若拒绝原假设，则意味着模型需要设定多个转换函数。表1的结果显示，所有模型均未能拒绝原假设，表明模型1～6均设定一个转换函数是恰当的，即r=1。

4.位置参数的个数确定

在确定了转换函数个数r之后，就需要进一步确定各个模型转换函数的位置参数个数m。文章对6个模型分别在m=1和m=2的情况进行PSTR估计。根据AIC和BIC信息准则确定位置参数m的最优个数，结果见表2，m=1。

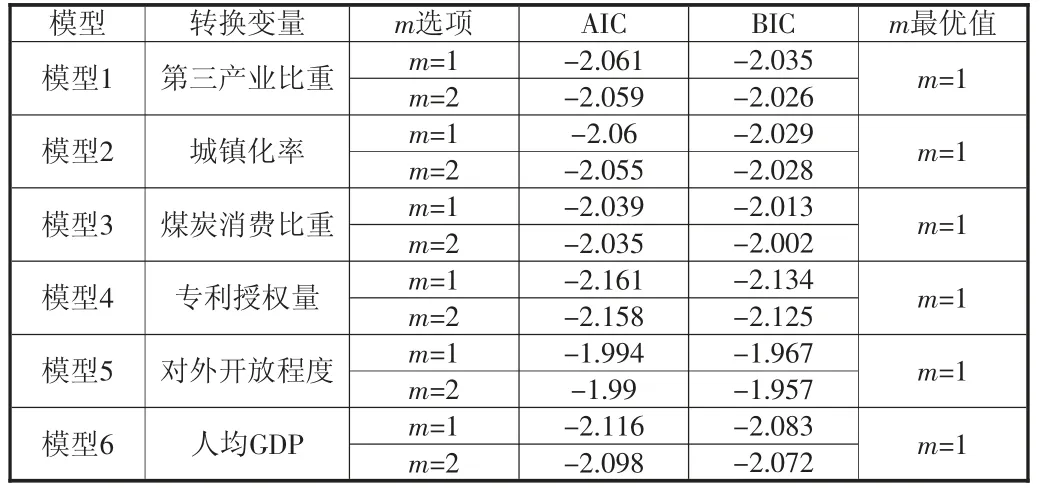
表2 PSTR模型参数确定结果

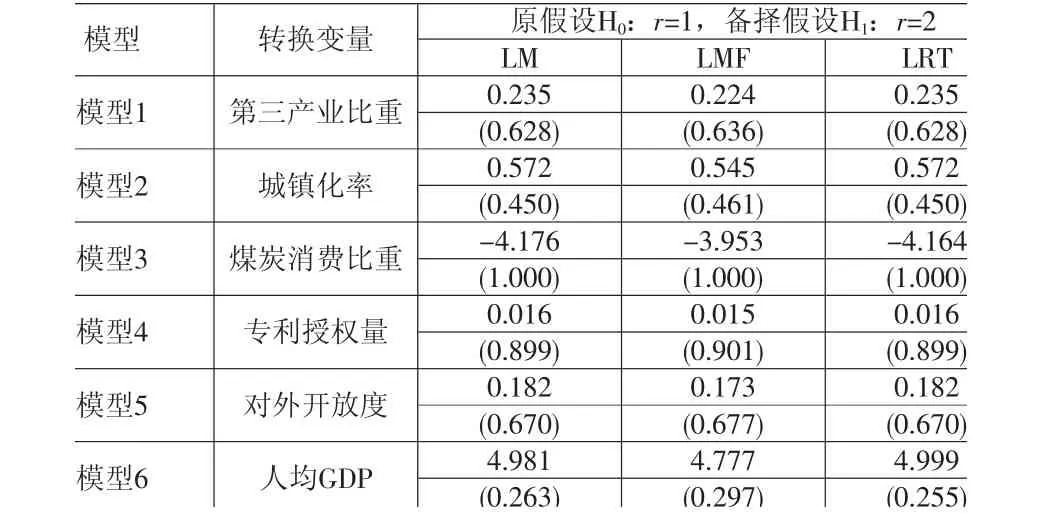
表1剩余非线性检验结果

5.PSTR模型回归结果

在确定转换函数个数r与位置参数个数m后，通过网络格点搜索法寻找转换函数的位置参数c和斜率系数γ的最优组合，从而获得转换函数G的具体表达式。将转换函数带入PSTR模型1，使用非线性最小二乘法进行参数估计，得到解释变量在不同机制下的回归系数，回归结果见表3。可以看到，模型1～6的回归系数均在1%水平下显著。

表3 PSTR模型回归结果

6.转换变量对经济增长与碳排放关系的影响分析

（1）第三产业比重对二者关系的影响分析

模型1分析经济增长对碳排放的影响系数随第三产业比重变化而发生平滑转换的情况。由表3可知，模型1存在单一门槛值c为0.7343，人均GDP线性部分的系数β0=1.0331＞0，而非线性部分的系数β1=-1.5768＜0。综合这两部分，可以确定经济增长对碳排放影响系数的取值范围在理论上为[-0.5437，1.0331]。

图1绘制了转换函数和影响系数的变化曲线，转换函数的最小值为0.0484，最大值为0.6515，转换速度适中，建模效果较为理想。随着第三产业比重的不断增加，影响系数在高、低区制间平滑转换，其取值范围在实际中为[0.0057，0.9568]，当第三产业比重低于0.7343时，经济增长对碳排放存在显著的正向促进作用，影响系数最大为0.9568，而当第三产业比重高于0.7343，经济增长对碳排放的正向促进作用逐渐减弱，影响系数最终减小至0.0057＞0，并未出现理论上的最小值-0.5437，因此，截止到2019年，中国仍处于EKC曲线的爬坡阶段，拐点尚未出现。究其原因，由图1可以看出，1997—2019年大部分样本观测值仍处于低区制内，第三产业比重较低。由表4可以看到，截止到2019年，第三产业比重跨越门槛值的省份只有北京，因此，其他省份应着力于经济产业结构优化，提升第三产业比重，尽早跨越门槛值，转换函数的数值才会从0.6515继续增加至理论值1，影响系数的数值才会从0.0057继续下降至理论值-0.5437，中国才会越过拐点进入EKC曲线的下坡阶段。

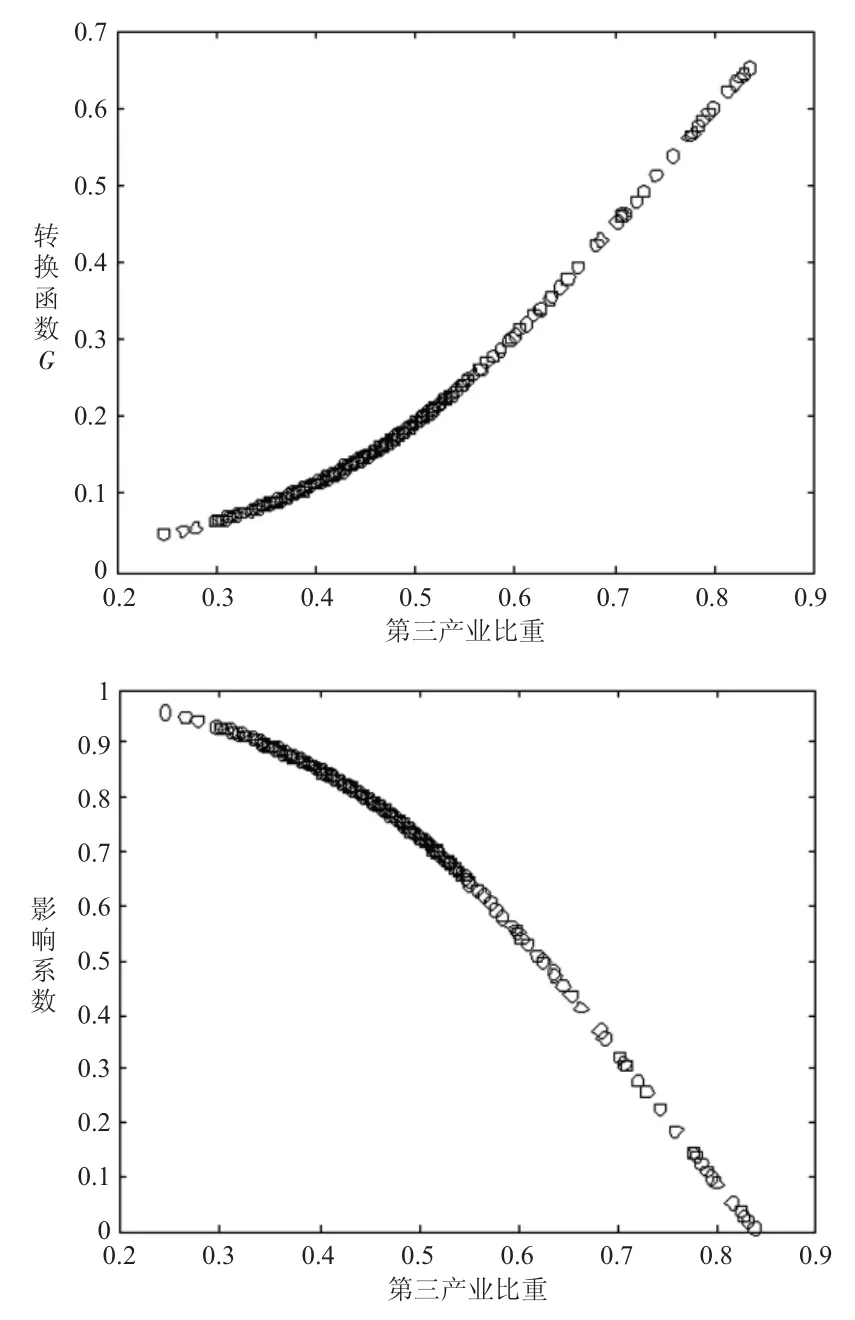
图1模型1的转换函数及影响系数平滑转换图

（2）城镇化率对二者关系的影响分析

模型2分析经济增长对碳排放的影响系数随城镇化率变化而发生平滑转换的情况。由表3可知，模型2存在单一门槛值c=0.8375，人均GDP线性部分的系数β0=0.9035＞0，而非线性部分的系数β1=-1.1196＜0，因此，经济增长对碳排放影响系数的取值范围在理论上为[-0.2161，0.9035]。

图2绘制了转换函数和影响系数的变化曲线，最小值为G=0.0037，最大值为G=0.6153，并在二者之间实现了平滑转换。随着城镇化率的不断提高，经济增长对碳排放的影响系数在高、低区制间平滑转换，其取值范围在实际中为[0.2147，0.8993]，当城镇化率低于0.8375时，经济增长对碳排放存在显著的正向促进作用，影响系数最大为0.8993，而当城镇化率高于0.8375，经济增长对碳排放的正向促进作用逐渐减弱，影响系数最终减小至0.2147＞0，并未出现理论上的最小值-0.2161，因此，截止到2019年，中国仍处于EKC曲线的爬坡阶段，拐点尚未出现。其原因在于，由图2可以看出，1997—2019年大部分样本观测值处于低区制内，城镇化率较低。由表4可以看出，截止到2019年，城镇化率跨越门槛值的省份只有北京、上海、天津。因此，中国其他省份应加快城镇化进程，使城镇化率尽早跨越门槛值，转换函数的数值才会继续从0.6153增加至理论值1，影响系数的数值才会继续从0.2147下降至理论值-0.2161，中国才会越过拐点，进入EKC曲线的下坡阶段。

（3）煤炭消费比重对二者关系的影响分析

模型3分析经济增长对碳排放的影响系数随煤炭消费比重变化而发生平滑转换的情况。由表3可知，模型3存在单一门槛值c=0.397，人均GDP线性部分的系数β0=0.0743＞0，非线性部分的系数β1=1.0522＞0，综合这两部分，经济增长对碳排放的影响系数的取值范围在理论上为[0.0743，1.1265]。

图3绘制了转换函数和影响系数的变化曲线，随着煤炭消费比重的不断降低，经济增长对碳排放的影响系数在高、低区制间实现平滑转换，其取值范围在实际中为[0.1473，1.1017]。当煤炭消费比重大于0.397时，经济增长对碳排放存在显著的正向促进作用，影响系数最大为1.1017，而当煤炭消费比重小于0.397，经济增长对碳排放的正向促进作用逐渐减弱，影响系数最终减弱至0.1473，并未出现理论上的最小值0.0743，因此，由表4可以看出，截止到2019年，中国仍处于EKC曲线的爬坡阶段，拐点尚未出现。其原因在于，由图3可以看出，1997—2019年大部分样本观测值处于高区制内，煤炭消费比重较高。截止到2019年，煤炭消费比重跨越门槛值的省份只有北京、上海、天津、海南、广东。因此，中国其他省份应加快能源结构低碳化，降低煤炭消费比重，尽早跨越门槛值，这样，影响系数的数值才会从0.1473继续减少至理论值0.0743。

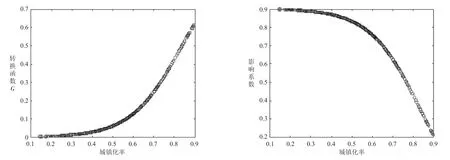
图2模型2的转换函数及影响系数平滑转换图

图3模型3的转换函数及影响系数平滑转换图

（4）专利授权量对二者关系的影响分析

模型4分析经济增长对碳排放的影响系数随专利授权量变化而变化的情况。由表3可知，模型4存在单一门槛值c=9.1561，人均GDP线性部分的系数β0=1.1265＞0，而非线性部分的系数β0=-0.6497＜0，因此，经济增长对碳排放影响系数的取值范围在理论上为[0.4768，1.1265]。

转换函数和影响系数的变化曲线如图4所示，随着专利授权量的不断增加，经济增长对碳排放的影响系数在高、低区制间平滑转换，其取值范围在实际中为[0.4795，1.1259]，与理论取值区间很接近。当专利授权量小于9.1561时，经济增长对碳排放存在显著的正向促进作用，影响系数最大为1.1259，而当专利授权量大于9.1561，经济增长对碳排放的正向促进作用逐渐减弱，影响系数最终减弱至0.4795＞0，因此，由表4可以看出，截止到2019年，中国仍处于EKC曲线的爬坡阶段，拐点尚未出现。由图4可以看出，1997—2019年大部分样本观测值处于高、低区制之间，分布在位置参数c=9.1561两侧，各省技术水平正在不断提升，处于关键的转型期。截止到2019年，除新疆、宁夏、海南、青海之外，中国其余省份专利授权量均已跨越门槛值，技术减排效应正在发挥积极作用。

（5）对外开放度对二者关系的影响分析

模型5分析经济增长对碳排放的影响系数随对外开放度变化而变化的情况。由表3可知，模型5存在单一门槛值c=0.4049，人均GDP线性部分的系数β0=0.8328＞0，而非线性部分的系数β1=-0.4003＞0，因此，经济增长对碳排放影响系数的取值范围在理论上为[0.4325，0.8328]。

转换函数和影响系数的变化曲线如图5所示，随着对外开放度的增加，经济增长对碳排放的影响系数的取值范围在实际中为[0.4325，0.8209]，与理论取值区间很接近。当对外开放度小于0.4049时，经济增长对碳排放存在显著的正向促进作用，影响系数最大为0.8209，而当对外开放度大于0.4049，经济增长对碳排放的正向促进作用逐渐弱化，影响系数最终减小至0.4325＞0，因此，由表4可以看出，截止到2019年，中国仍处于EKC曲线的爬坡阶段，拐点尚未出现。由图5可以看出，1997—2019年大部分样本观测值处于低区制内，对外开放度较低。截止到2019年，对外开放度跨越门槛值的省份只有北京、上海、天津、广东、浙江、江苏。因此，中国其他省份应加大对外开放力度，尽早跨越门槛值，实现经济增长对碳排放影响系数从低区制向高区制的转换。

（6）中国EKC曲线检验

模型6以人均GDP为转换变量，对中国EKC曲线进行检验。由表3可知，模型6存在单一门槛值c=1.2243，人均GDP线性部分的系数为β0=0.9830＞0，而非线性部分的系数为β1=-0.5739＞0，综合这两部分，经济增长对碳排放影响系数的取值范围在理论上为[0.4091，0.9830]。

转换函数和影响系数的变化曲线如图6所示，随着人均GDP的不断增加，经济增长对碳排放影响系数在高、低区制间平滑转换，其取值范围在实际中为[0.4293，0.9828]，与理论取值区间很接近。当人均GDP小于1.2243时，经济增长对碳排放存在显著的正向促进作用，影响系数最大为0.9828，而当人均GDP大于1.2243，经济增长对碳排放的正向促进作用逐渐减弱，影响系数最终减弱至0.4293＞0，因此，截止到2019年，经济增长仍然会带来碳排放的增长，两者关系仍处于EKC曲线的爬坡阶段，目前尚未达峰。

由图6可以看出，1997—2019年大部分样本观测值处于低区制内，大部分样本的人均GDP尚未跨越门槛值。由表4可以看出，截止到2019年，多数省份人均GDP均实现跨越门槛值1.2243。随着中国经济增长方式的转变，产业和能源结构的优化，经济发展动力的增强，中国其他省份人均GDP将逐渐跨越门槛值，经济增长对碳排放的影响系数将会持续降低，二者关系不断向EKC曲线的拐点趋近，直至由正转负，实现碳达峰并进入EKC曲线下坡阶段。

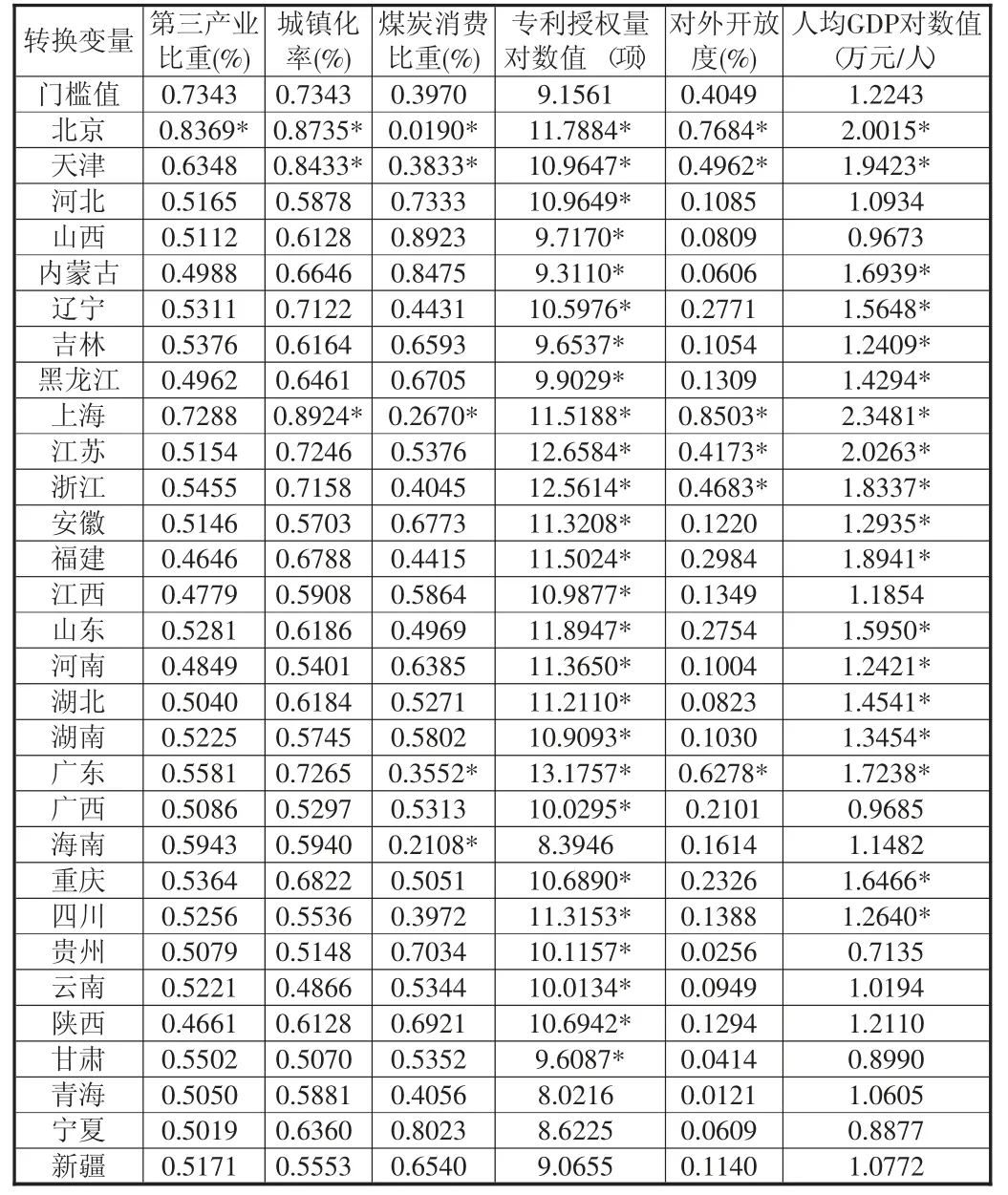
表4 2019年中国各省份转换变量门槛值跨越情况统计表

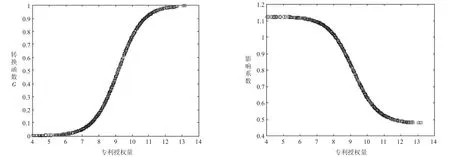
图4模型4的转换函数及影响系数平滑转换图

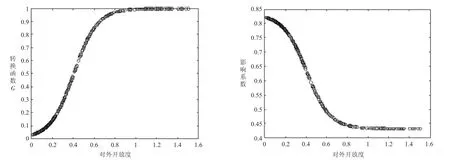
图5模型5的转换函数及影响系数平滑转换图

四、结论与建议

1.研究结论

第一，中国经济增长对碳排放的影响系数不断降低，但始终为正，因此中国尚处于EKC曲线的爬坡阶段，拐点尚未出现；第二，除新疆、宁夏、海南、青海之外，中国其余省份专利授权量均已跨越门槛值，中国的技术减排效应已经凸显；第三，除北京、上海、天津、广东、海南、江苏、浙江外，其他省份的第三产业比重、城镇化率、煤炭消费比重、对外开放度均未跨越门槛值，中国经济增长对碳排放的影响系数还有很大下降空间；第四，中国达到EKC曲线顶峰并进入下坡阶段的关键在于提高第三产业占比和城镇化率，这两个转换变量对应的转换函数值均为0.6左右，远未达到理论值1，只有不断进行产业结构优化调整，加快绿色城镇化进程，经济增长对碳排放的影响系数才会由正转负，促进中国“双碳”目标与“两步走”目标的同时实现。

图6模型6的转换函数及影响系数平滑转换图

2.政策建议

第一，技术进步在中国碳减排进程中已经发挥了积极的作用，为了实现碳减排目标和经济增长目标，未来需进一步加大研发投入，并不断优化投入结构，重点扶持低碳能源技术研发。

第二，中国跨越EKC曲线拐点的关键在于两点：其一，不断促进产业结构绿色升级。控制第二产业低附加值、高能耗、高排放的行业增长，大力发展资源节约型和环境友好型的特色产业，壮大新兴产业和现代服务业。其二，高效推进绿色城镇化进程。坚持以新发展理念为指导，将生态文明理念贯彻到新型城镇化建设中，持续推进城镇绿色低碳发展。

第三，部分省份的煤炭消费比重较高，需深入推进能源结构转型，大力发展风能等新能源，扩大清洁能源消费比例。

第四，持续扩大高水平对外开放，横向扩大国际合作的范围，纵向提高国际分工的层次，积极发展低污染、高附加值的现代服务贸易，有利于解除经济增长的“高碳锁定”。