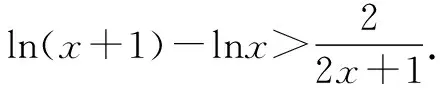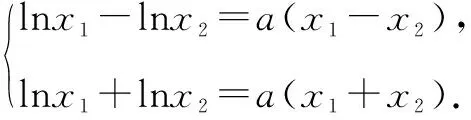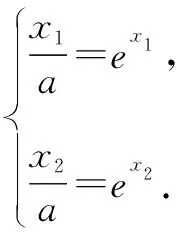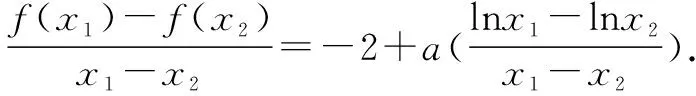对数均值不等式及其应用
2022-12-10黄瀚元
数理化解题研究 2022年31期
黄瀚元
(广西壮族自治区柳州高级中学 545006)

在近些年的高考与模拟考试卷中,以上述不等式为背景的试题屡见不鲜,如果我们能掌握并熟练运用上述不等式,那么我们的解题思路就可以清晰自然,解题过程就可以简洁通畅,为此,我们有必要对此不等式做深入研究.
1 对数均值不等式的证明

下面我们来证明这个不等式.
不失一般性,不妨设a>b.




所以函数f(x)在区间(1,+∞)单调递减.
故f(x) 所以函数g(x)在区间(1,+∞)单调递增. 故g(x)>g(1)=0. 证毕. 结合上述证明过程,我们可以得到两个重要的不等式链: 用图象表示如图1、图2所示: 图1 图2 如果我们把对数均值不等式中的a,b分别用ea,eb替换,则可得到: 我们把它叫做指数均值不等式. 证明由对数基本不等式可知 把上式中的a,b分别用x+1,x替换,得 证明由对数基本不等式可知 把上式中的a,b分别用n+1,n替换,得 证明由对数基本不等式可知 例4 方程lnx=ax有两个不相等的实数解x1,x2,证明:x1+x2>2e. 由对数均值不等式可得 所以lnx1+lnx2>2⟺x1x2>e2. 例5 已知函数f(x)=x-aex有两个不同的零点x1,x2,求证:x1+x2>2. 又因为x1,x2是f(x)的两个极值点, 所以x1>0,x2>0,且x1+x2=a,x1x2=1. 又由对数均值不等式可知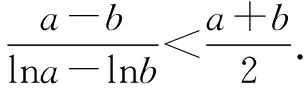
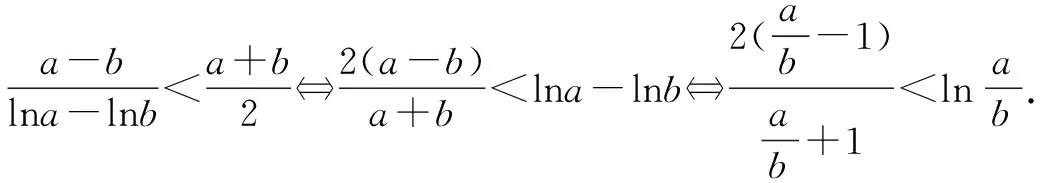
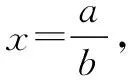

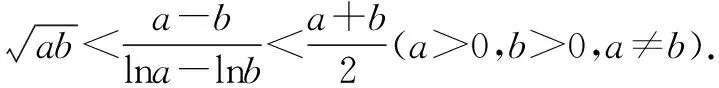
2 对数均值不等式的推论
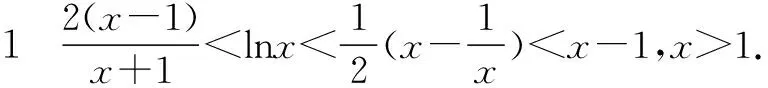


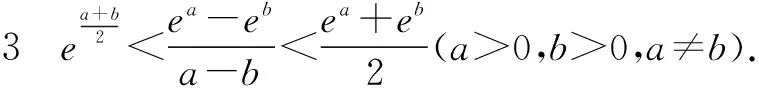
3 对数均值不等式的应用