斜面上斜抛运动情境的分析

何国泉

(江苏省如皋中学 226500)

分析斜面上斜抛运动情境，主要依据运动的分解以及运动学规律等知识.考虑到部分习题具有一定技巧，为使学生少走弯路，提高效率，应结合实际情况做好经典习题地筛选以及讲解，更好地拓展学生视野，尤其预留时间要求学生做好听课地总结，将细节把握到位，真正地实现灵活应用.

1 理论讲解

斜面上运动做斜抛运动通常构建平面直角坐标系，将初速度进行成水平以及竖直两个方向.其中在水平方向上物体做匀速直线运动，在竖直方向物体做具有初速度的匀加速运动.求物体在斜面上的运动时间是解答该类运动情境的关键.那么该如何进行处理呢？

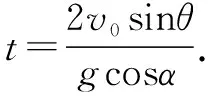
2 案例分析

例1运动员滑雪的可简化为如图1所示的情境.一可视为质点的运动员从倾角为α=30°的斜面顶端O点以v0=20m/s的初速度飞出.初速度方向和斜面的夹角θ=60°，虚线为运动员的运动轨迹，其中A为运动员运动示意图运动轨迹的最高点，B为轨迹上离斜面最远的点，C为过B点作竖直线和斜面的交点，忽略空气阻力，g取10m/s2.求：(1)运动员从A点运动到B点的时间；(2)O、C两点间的距离.

图1

答案：(1)5m/s (2)40m

为更好地锻炼学习者分析该问题的能力，课堂上预留以下问题，要求其思考解答：该如何求解BC之间的距离？

例2如图2将一光滑斜面ABC固定在水平面上.其中AC=BC=2.5m.一可视为质点，质量m=1kg的小球，从斜面底端A以vA=10m/s的初速度冲上斜面，刚好沿P点切线进入到口径很小的光滑圆管轨道中.其中轨道圆心为O，半径R=1m.OP和竖直方向的夹角θ=60°，Q点为轨道最高点，忽略空气阻力，g取10m/s2.求：(1)小球从B点抛出后在空中运动到最高点时的速度；(2)小球从A点运动到P点所有的时间；(3)小球在Q点对圆弧轨道的作用力.

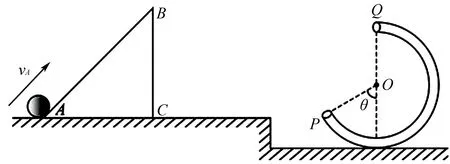
图2

该题为斜面上斜抛运动和圆周运动的综合题.解题的关键在于搞清楚小球运动过程中角度以及速度关系，结合实际情况对其运动进行合理分解.

答案：(1)5m/s.

(3)60N.

例3近年来充气弹跳飞人娱乐项目受到人们的喜爱.娱乐过程可简化为如图3所示的情境.娱乐者躺在可看做斜面的气包AC上的P点.斜面和水平方向的夹角θ=37°.工作人员从站台蹦到气包上.娱乐者被弹起后以和斜面垂直的方向飞出，经过最高点O落到B点.其中B点和O点竖直方向的距离h=3.2m，水平距离l=2.4m.AB处在同一水平面上.不考虑空气阻力，g取10m/s2.则( ).

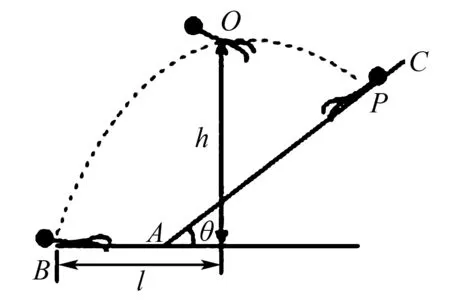
图3

A.P点到B点的位移为3.6m

B.AB之间的距离为0.4m

C.从P点到B点的运动时间为1s

D.从P点到B点中的最大速度为9m/s

该题考查的知识点较多.解题时既需对娱乐者的运动速度进行分解，又需要运用几何知识以及三角函数求出对应参数的值.该题的计算量较大，计算时应认真仔细，采用不同字母表示对应参数，避免混淆.

答案：C.

例4如图4，将一截面呈直角三角形的劈形物块固定在水平地面上.斜面高h=4m，左侧倾角α=37°，将一小球以v0=9m/s的初速度从C点沿斜面抛出，且落在AB面上后不反弹.忽略一切阻力.重力加速度g为10m/s2( ).

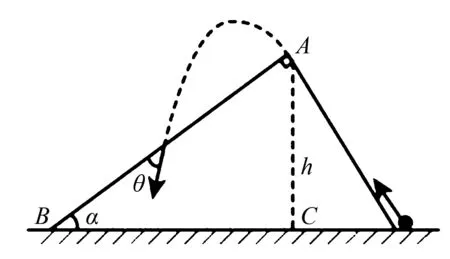
图4

A.小球到达A点的速度为8m/s

B.小球在空中运动的时间为0.16s

C.小球达到最高点后下落的时间为0.17s

基于斜面上做斜抛运动的规律的积累与应用，很容易判断出ABC三项的正确与否.D项相对来说具有一定难度，需灵活应用匀速直线运动规律，并结合几何知识，理清角度之间的内在联系.

斜抛运动看似较为较为复杂，可联系所学知识将速度、加速度进行特定方向上的分解，以更好地运用平抛或者匀加速运动相关规律，尤其为更好地解答斜面上的斜抛运动问题，应注重做好以下几点：

其一，做好斜抛运动和平抛运动规律的对比，找到两者之间的异同点，尤其注重从研究平抛运动规律中获得启发，寻找分析斜抛运动的思路.根据要求解的问题建立合适的平面直角坐标系，以降低速度、加速度分解难度.

其二，为提高解题效率，应做好不同情境习题的筛选，借助多媒体技术为学生展示物体的具体应用过程，深化其对物体做斜抛运动地认识，促使其更好地找到解题切入点.同时，引导学习者注重运用运动学公式以及几何知识构建物理方程，推导、牢记相关结论，在以后解题中直接套用，并做好运用地总结，及时发现与弥补运用中的不足.

其三，分析斜抛运动情境时不能满足于得出正确结果，应尝试着进一步挖掘习题价值，尝试着对习题进行改编，而后进行分析，加深对习题印象的同时，更好地锻炼解题灵活性.不仅如此，注重引导学生学会学习，既要定期进行错题重做，又要多与其他学习者交流解题经验，学习他人长处，不断提升自身解题技能.