利用圆锥曲线的相似性解决一类问题

唐宜钟

(陕西省汉中市龙岗学校 723100)

1 问题提出

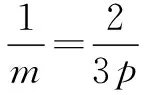
由于含有多个字母，且中间涉及换元技巧，有一定难度. 作为选择题，多数学生运用特值法，令抛物线为y2=4x(p>0)，可得

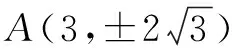
换用其他特值，依旧成立.于是笔者猜测：所有抛物线都相似，它们对应线段长所成比例表达式存在某种形似.

2 问题证明

曲线相似定义：已知图形C1与图形C2，若两个图形上的点之间存在一一对应关系，且图形C1上任意两点的距离与图形C2上两对应点的距离之比是常数k(k≠0),我们称这两个图形相似，把k称为图形C1对图形C2的相似比.

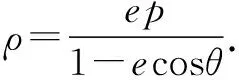
如图1，把两个圆锥曲线C1和C2平移使得相应的焦点重合于点F，从点F任意作一条射线分别与两曲线交于点P1与P2，则

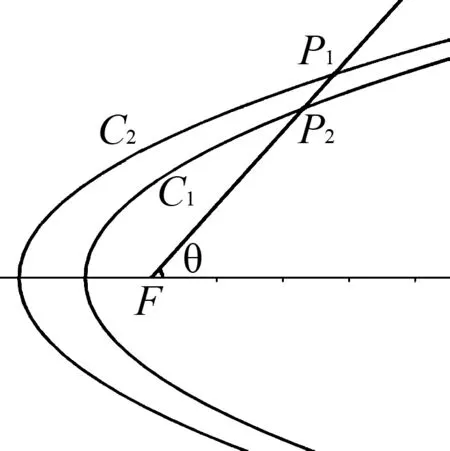
图1

特别地，当e1=e2=1时，共焦点的抛物线是相似的，相似比等于焦准距之比，相似中心为焦点.

又相似比也等于通径之比，故开口相同的抛物线平移到同一顶点也相似，相似中心为顶点. 通过旋转，不同开口方向的抛物线可以统一开口方向.

故所有的抛物线都相似，相似比为焦准距之比(通径之比).

3 高考运用

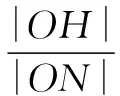
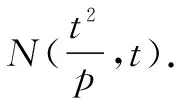
可认为点H在抛物线C:y2=2px(p>0)上，点N在抛物线C′:y2=px(p>0)上.

显然抛物线C与C′相似，相似中心为顶点.

例2(2019年浙江卷)如图2，已知点F(1,0)为抛物线y2=2px(p>0)的焦点，过点F的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且点Q在点F右侧.记△AFG,△CQG的面积为S1,S2.

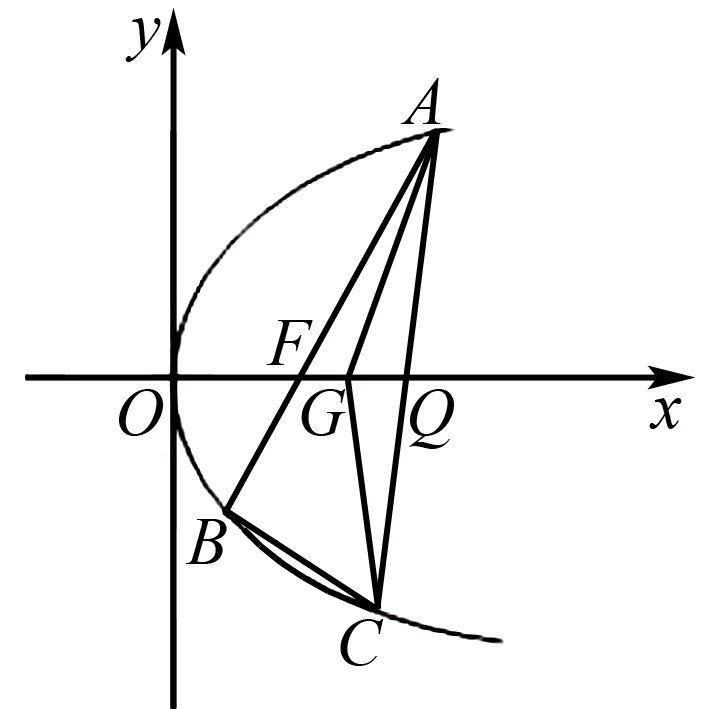
图2

(1)求P的值及抛物线的标准方程；

解析(1)y2=4x；

由A，F，B三点共线得kAB=kAF.

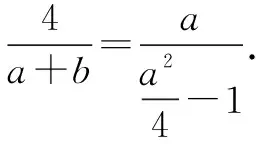
从而ab=-4.

同理可得ac=-4q.

由三角形重心公式,得

c=-a-b，

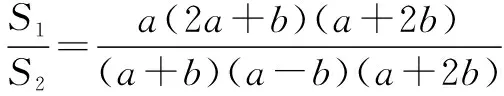
由于所有抛物线都相似，故其对应三角形面积之比为相似比的平方.本题是两个三角形面积之比，故对任意抛物线，面积比例式应该相同.

事实上，若抛物线为y2=2px(p>0)，仿照上述解法，可得

ab=-p2，ac=-2pq.

即c=-a-b，

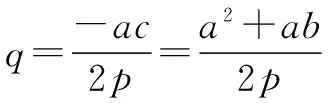
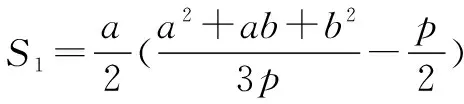
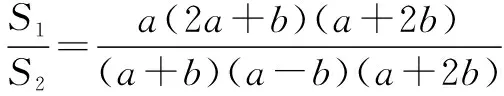
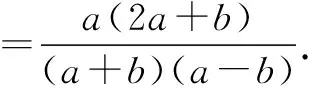
可见，对任意抛物线，本题结果都不变.

4 结论推广

通过上述证明，说明离心率相同的共焦点椭圆(双曲线)相似.

可得到两个椭圆(双曲线)的长轴、短轴或焦点对应成比例，则它们相似，相似中心可以为中心与顶点.

即两个椭圆(双曲线)只要离心率相同，在对应顶点重合，或中心重合，或对应焦点重合的前提下，都是相似的，相似比为焦准距之比(通径之比).