特值法在解题中的应用

程永军

(江苏省南京市雨花台中学 210000)

高中数学的集合、函数、不等式、空间立体几何等重要知识点是高考拉开学生成绩的关键，也是让许多高中生焦头烂额的学习难点.高考考场时间寸秒寸金，一些题目按照传统的运算步骤耗时耗力，一步运算出错就会前功尽弃.因此，广大高中数学教师要在日常的教学过程中加强填空题、选择题的特殊值教学工作，让学生学会巧代特殊值，不断积累特殊值求解的经典例题，从而为数学解题寻找捷径，提高数学答题效率，最终取得优异的高考数学成绩.

1 特值法在解题中的重要性

1.1 开拓学生思维

高中数学解题中的特值法可以节省解题时间，在最短的时间内得出正确答案，为后续的解题提供充足的时间.其特值不单是指特殊值，也指特殊点、特殊数列、特殊几何等，只要在题目当中属于特殊情况就都可以将其代入题目中，利用这些特殊值来快速地解决，得出问题的正确答案.特殊值法不仅能够开拓学生的思维，而且能够帮助学生形成发散性思维.除此以外，特殊化比一般化更为重要.特殊化策略是将原问题视为一般，构造其特殊问题，通过对特殊问题的分析而获得原问题的解决，特殊化策略是一种退的策略，所谓“退”，可以从复杂退到简单，从一般退到特殊，从抽象退到具体.在这种特殊值的方法下，能够有效促进学生的逻辑思维发展，帮助学生树立良好的思维意识.

1.2 把问题简单化

建构主义理论认为，学习不是教师单纯地进行教学，而是数学教师教会学生如何进行数学学习的过程 ，虽然学生在学习中没有过多地接触复杂、难懂、抽象的数学表达，没有过于丰富的解题经验，但是他们依照对数学思维的认识，会以较为形象、直观的方法表达他们对题意的解释.特值法就是他们生活经验与数学理解有效结合的形式之一，通过直观表达，学生从复杂的文字表述中提炼出重点词、关键句，简化了繁杂的题意，让思维更为简单、更有价值.不得不说，特殊化作为化归策略，其基本思想方法是很简单的，对于“一般”而言，“特殊”问题往往显得简单、直观和容易解决，并且在特殊问题的解决过程中，常常蕴含着一般问题的解决方法.所以，人们在解决某个一般性的数学问题遇到困难时，常常会想到先解决它的特殊情况，然后再把解决特殊问题的方法推广到一般问题.从形式上看，将一般问题特殊化是不困难的，但是某个一般性问题经过不同的特殊化处理后会得到多个不同的特殊化命题.

1.3 提高数学成绩

特值法作为高考中的基本数学方法，多数时候用于选择题和填空题，通过找到题目的特殊值，将其代入到所解的式子中，将问题简单化，不仅能够提升学生的学习效率，而且适用于考试这一特殊场景中，帮助学生在短时间内得到高的分数，同时又能够锻炼学生的发散性思维和逻辑思维.特殊值法的解题依据和逻辑基础是，如果某个结果对一般情况适用，那么对特殊情况也适用；如果对特殊情况适用，那么对一般情况不一定是适用的；如果对特殊情况不适用，那么对一般情况也一定不适用.这是一个非常简单的思维逻辑.

2 特值法在高中数学解题中的应用

2.1 特值法帮助学生灵活运用数学知识

高考试卷有送分题和拉分题两种题型，送分题用传统的解题方法即可求解，但拉分题按照传统作答方式步骤十分繁琐，考场时间寸秒寸金，出题人意在选拔具有创新数学思维、灵活运算技巧的优秀数学人才.因此，广大教师要引导学生充分利用高考真题活化自己的数学思维，提升数学运算速度和答题正确率.

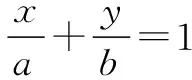
A.a2+b2≤1 B.a2+b2≥1

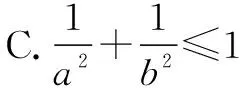
这道试题重点考查学生的直线函数与三角函数知识，同时这是一道选择题，教师要鼓励学生“小题小做”，采用排除法或特值法进行求解.教师可以引导学生运用多种方式进行解答.

(2)特殊公式法.教师要鼓励学生多用巧力解题，灵活运用平常记忆的特殊公式解题，该直线函数正好等于1，由sin2α+cos2α=1可知点M在单位圆上，再由题目可知直线与单位圆有交点，接着运用直线与圆的距离公式便可求解.

(4)关于“1”的平面向量法.教师可以指引学生利用平面向量数量积坐标运算法则进行解答.

2.2 特值法帮助学生培养灵活数学运算思维

特值法不同于循规蹈矩的传统数学运算，它需要学生在熟练掌握教材知识的基础上灵活运用知识，结合题干给出的特殊点、特殊直线、特殊函数、特殊几何图形，并根据自己的作答经验寻找最快捷的解题方法.另外，特值法还可以帮助学生锻炼数学思维、积累数学运算技巧.

题2 定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x，y∈R)，f(1)=2，则f(-3)等于( ).

A.2 B.3 C.6 D.9

该题是一个典型的抽象函数题，传统的解题方法是反复赋值、重复运算，而特殊值则令x=n，y=1，接着运用题干所给的关系式将函数f(x)转化为函数f(n)，或者求出f(0)，f(3)的数值，进而求得函数f(n)的解析式，然后利用函数f(n)的解析式求得答案，这样便可以把抽象函数转化为带有解析式的普通式方程，为学生节省大量的运算时间.

另外，“特值法”指的是特殊代替一般，但并不改变试题的根本性质，这一特点便表明特殊值代入、特殊值转换、特殊函数构造等都是题目作答的一种特殊情况.大多数学生擅长利用传统方式作答，特值法可以看成是对传统作答方法的一种补充.

2.3 寻找满足特值法使用的条件

使用特值法需要考虑一定的限制条件，代入特殊数值不能影响最后的运算结果，其次，代入的量要与题干所给的关系式紧密对应.针对某些试题，一般条件成立，特殊条件也能成立，但特殊条件成立，一般条件可能不成立.许多学生为了省时省力盲目使用特值法解题，经常把0，1等数值直接代入题干公式中，这可能导致使用传统的简单运算就能解答的送分题变成夺命题，最终让学生丧失了对特值法的使用信心.因此，广大高中数学教师要积极培养学生善于从题干中剥离条件、细心分析的能力，并让学生养成题后检查的习惯.

题3已知y=loga(2-ax)在区间[0，1]上单调递减，则a的取值范围为( ).

A.(0，1) B.(0，2) C.(1，2) D.[2, +∞)

该题是一道指数对数函数问题，由对数知识可以得到a>0，且a≠1，由此可以运用排除法，将B选项排除掉.又因为函数在区间[0，1]为单调递减，A选项明显不符合.教师可以让学生细心观察剩下的C，D选顶，并发现其中的规律，如C，D选项都有数值2，这时，教师便可以引导学生利用特值法并结合对数函数成立条件，如果特殊值2不能满足题干要求，则该选项必定是错误的，学生不用再考虑其他数值，最终选择C选项.

2.4 特值法是解决填空难题的有效方法

高中数学填空题也是特值法常见的应用题型，常见的应用类型有求代数的取值范围、直接求值、几何图形等.

该题型需要学生运用三角形、等差数列、三角函数等知识进行求解，传统的数学求解需要运用三角函数公式进行复杂代换，而运用特值法可以一分钟内求得结果.学生在作答前要认真阅读填空题的题干，精准把握题目要求，如该题目要求三角形三边长为等差数列，我们不妨取等边三角形直接代入计算，令三个角都为60°，便可以轻松得到结果，这样既满足题目所给出的条件限制，又能帮助学生快速作答.另外，填空题不同于选择题，学生没有可以参考的选项，必须从题干中多挖掘隐藏的信息，结合教材知识，寻找可以满足题干要求的特殊值代入计算.

总之，特值法求解可以帮助学生快速、高效作答，利于学生节省更多宝贵的考场时间攻克后面难度较大的压轴题，高中数学老师要在日常的教学工作中引导学生多思考、多提问，争取做到一题多解、一法多用，从而帮助学生取得优异的高考数学成绩，实现人生理想！