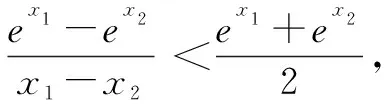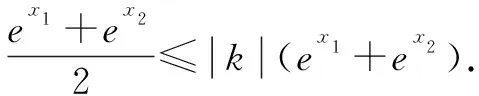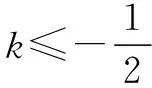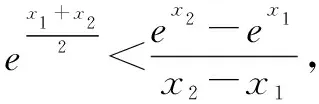一个不等式的发现及其应用举例

刘海涛

(安徽省芜湖市第一中学 241000)

1 问题的提出

在近些年的高考和各类模拟考中，频繁出现与lnx，ex有关的双变量问题，这类问题的常用解法是构造函数将双变量问题转化为单变量问题，处理方法有比值代换或差值代换，但是过程繁琐，技巧性强，运算量大，学生不易掌握.文[1]介绍了对数均值不等式，使得关于lnx的双变量问题难度降低，为解决该类问题提供了新思路和新方法，但是关于ex的双变量问题怎么办呢？笔者通过研究，发现由对数均值不等式可以得到一个关于ex的不等式链，可以用其解决一类关于ex的双变量问题.

2 指数均值不等式的介绍

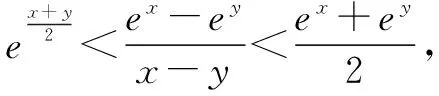
3 指数均值不等式的应用举例

3.1 在函数零点问题中的应用

例1已知函数f(x)=2ex-x2-ax.若f(x1)=f(x2)，且2x0=x1+x2，问：函数f(x)在点(x0,f(x0))处的切线是否与x轴平行？

解析由题意，得

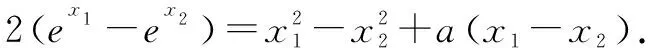
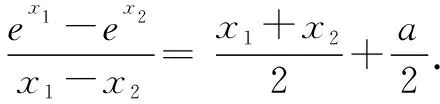
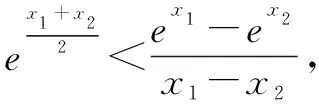
函数f(x)求导得

f′(x)= 2ex-2x-a.

则f′(x0)=2ex0-2x0-a<0.

故函数f(x)在点(x0,f(x0))处的切线不与x轴平行.

3.2 在比较大小问题中的应用

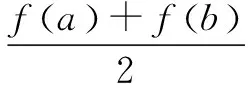
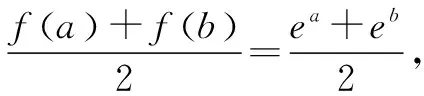
由指数均值不等式可得

评注该题是2013年陕西高考理科数学的压轴题，若考生在备考阶段学习过指数均值不等式，考场上便可信手拈来.

3.3 在证明不等式问题中的应用

例3已知函数f(x)=xe-x(x∈R).如果x1≠x2，且f(x1)=f(x2)，证明：x1+x2>2.

解析由题知x1e-x1=x2e-x2.

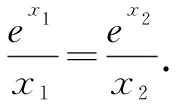
由分式的和比、差比性质,得

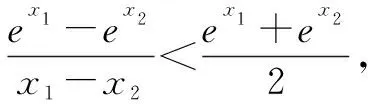
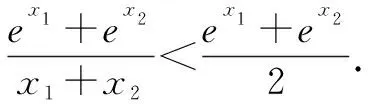
故x1+x2>2.

例4已知f(x)=ex-mx.若x1,x2(x12.

解析由题知ex1-mx1=ex2-mx2=0.

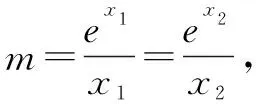
评注例3是2010年天津高考理科数学的压轴题，例4是2018 年全国高中数学联赛福建省预赛第 14 题，两道题官方给出的参考答案是采用对称化构造函数的方法证明，难度大，对学生思维要求高，考生不易解答，但是该题利用指数均值不等式可以快速解答，过程简洁自然，给人耳目一新的感觉.

3.4 在求参数范围问题中的应用

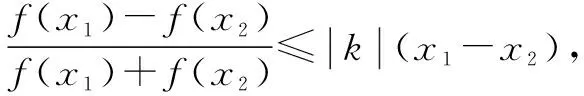
解析由题意，得

不妨设x1

评注该题运用指数均值不等式的右边恰到好处地放缩了原不等式，快速地获得了关于参数k的不等关系，简洁地求得了k的取值范围.

例6已知函数f(x)=x2+ax+1，g(x)=ex(其中e为自然对数的底数).若对任意x1,x2∈[0,2](x1≠x2),不等式|f(x1)-f(x2)|<|g(x1)-g(x2)|均成立, 求实数a的取值范围.

即|(x1-x2)(x1+x2+a)|<|ex1-ex2|.

不妨设0≤x1

即-et-2t≤a≤et-2t.

设m(t)= -et-2t，φ(t)=et-2t，

易知m(t)在(0,2)上单调递减，

则m(t)

求导得φ′(t)=et-2.

易得φ(t)在(0,ln2)上单调递减，在(ln2,2)上单调递增.

则φ(t)≥φ(ln2)=2-2ln2.

故-1≤a≤2-2ln2.

本文利用指数均值不等式给出了上述六道与ex有关的双变量问题的简便解法，让读者感受指数均值不等式的妙用，但是任何一种方法都有其局限性，我们在日常的学习中，要结合自身掌握程度和实际情况，选择最佳的解题方法，不可一味追求某一种解法，要学会从不同解法中汲取不同的数学思想，从而提高自身的数学核心素养与解题能力.