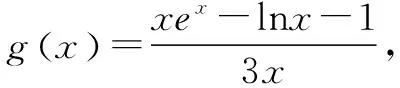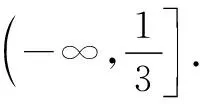逻辑推理素养指导下的解题活动
——发散思维,一题多解
2022-12-10杨苍洲
杨苍洲
(福建省泉州第五中学 362000)

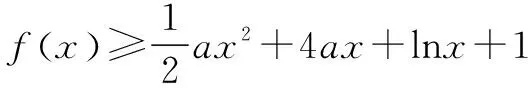
解法1先证xex-x-lnx-1≥0在(0,+∞)上恒成立.
令g(x)=xex-x-lnx-1(x>0),则
因为x>0,所以g″(x)>0.
所以g′(x)在(0,+∞)单调递增.
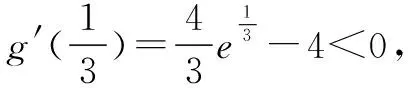
g′(1)=2e-2>0,
且当0 当x>x0时,g′(x)>0,g(x)单调递增. 故g(x)min=g(x0) =x0ex0-x0-lnx0-1. 由g′(x0)=0,得 即x0ex0=1,lnx0+x0=1. 因此g(x)min=g(x0)=0. xex-3ax-lnx-1≥g(x)≥0, 满足题意. xex-3ax-lnx-1 又g(x0)=0, 所以x0ex0-3ax0-lnx0-1 不满足题意. 分析2观察不等式的结构,从而产生联想,进行指对同构.观察到题中不等式包含指数与对数,且可以通过指对互化构造出相同的结构,因此,考虑直接同构进行化简放缩. xex-3ax-lnx-1≥0. 即ln(x·e3ax)-(x·ex)+1≤0. 令g(t)=lnt-t+1,则 当0 当t>1时,g′(t)<0,g(t)单调递减. 所以g(t)≤g(1)=0. 即lnt-t+1≤0,当且仅当t=1时,等号成立. 因为xex>0,所以 ln(x·ex)-(x·ex)+1≤0. ① 所以ln(x·e3ax)-(x·ex)+1≤ln(x·ex)-(x·ex)+1≤0,符合题意. 令h(x)=xex-1(x>0),则 h′(x)=(1+x)ex>0. 故h(x)在(0,+∞)单调递增. 又h(0)=-1<0,h(1)=e-1>0, 所以存在唯一x0∈(0,1),使得h(x)=0. 故当且仅当x=x0时,①式等号成立. 即ln(x0·ex0)-(x0·ex0)+1=0. 因此,存在x0∈(0,e),使得ln(x0·e3ax0)-(x0·ex0)+1>ln(x0·ex0)-(x·ex0)+1=0. 不符合题意. 分析3直接变参分离后,把问题转化为求最值的问题,再利用“隐零点”,设而不求,整体代换,求解最值. xex-3ax-lnx-1≥0. 由g′(x)=0,得 x2ex+lnx=0. 又因为y=xex在(0,+∞)单调递增, 即lnx+x=0. 令h(x)=lnx+x, 因为h(x)在(0,+∞)单调递增, 故当且仅当x=x0时,g′(x0)=0. 因为y=x2ex+lnx在(0,+∞)单调递增, 所以当0 所以g′(x)<0. 所以g(x)单调递减. 当x>x0时,x2ex+lnx>0,g′(x)>0,g(x)单调递增. 因此g(x)min=g(x0) xex-3ax-lnx-1≥0. 令g(t)=t-lnt-1,则 当0 当t>1时,g′(t)>0,g(t)单调递增. 所以g(t)≥g(1)=0. 即t-lnt-1≥0,当且仅当t=1时,等号成立. 因此xex-ln(xex)-1≥0. ② 令h(x)=xex-1(x>0),则 h′(x)=(1+x)ex>0. 故h(x)在(0,+∞)单调递增. 又h(0)=-1<0, h(1)=e-1>0, 所以存在唯一x0∈(0,1),使得h(x)=0, 此时x0ex0=1. 所以[xex-ln(xex)-1]min=x0·ex0-ln(x0·ex0)-1=0. 因为x>0,所以