一道2022年全国高中数学联赛预赛试题的几种解法

石秀成

(江苏省句容高级中学 212400)

1 试题呈现

这是2022年全国高中数学联赛重庆预赛试题的第7题，考查解析几何问题中的直线与圆、圆与圆的综合，属于高考难度，解答起来倒并不困难，但细品之下，本题可以从代数视角和几何视角等多个角度思考，解法多样，各具特色，因此本文从这些角度进行了一题多解，与读者共享.

2 解法探究

解法1(代数法)由题意联立，得

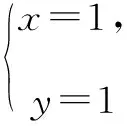
又点A在第一象限，所以A(1,1).

因此设直线CD:y-1=k(x-1)，

即kx-y+1-k=0.

解得k=5或1.

解法2 (参数方程法)由题意联立，得

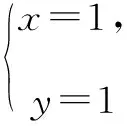
又点A在第一象限，所以A(1,1).

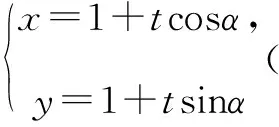
解得点C对应的参数为

t1=-2(cosα+sinα).

同理可得点D对应的参数为

t2=2(2cosα-sinα).

即-2(cosα+sinα)=4(2cosα-sinα).

解得tanα=5.

故k=5.

图1

所以D为AC的中点.

因为AC是圆O1的弦，

所以O1D⊥AD.

则以AO1为直径的圆(设圆心为O3)与圆O2相交于A，D两点.

由平面几何知识可知AC为两圆的根轴.

即AC⊥O2O3.

又O1(0,0)，A(1,1)，O2(3,0)，

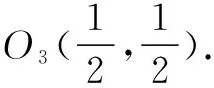
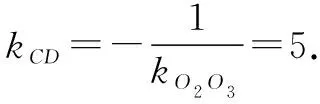
评注本解法从形的角度入手，首先通过垂直关系发现隐圆O3，进而通过平面几何知识观察出AC是圆O2和O3的根轴，借助根轴的性质可知AC⊥O2O3，而两圆的圆心坐标是显然的，因此直线AC的斜率是易得的. 本解法充分挖掘了条件的几何关系，以形显数，从形上揭示了几何问题的本质，过程简洁明了.

所以D为AC的中点.

设D(x0,y0)，取AD中点为M，由A(1,1)和D(x0,y0)，可得

因为O1D⊥AC和O2M⊥AC，

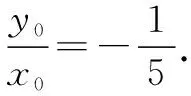
又kCD·kO1D=-1，所以kCD=5.

评注本解法将几何法和代数法融于一体，首先由垂直和平行的几何关系得以建立代数恒等式，再通过代数运算的化简得到参数之间的关系，进而达到求解问题的目标，这个过程深刻体现了数形结合的思想.

3 试题推广

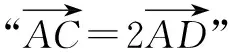
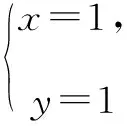
又点A在第一象限，所以A(1,1).

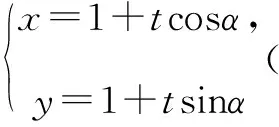
代入圆O1得t2+2t(cosα+sinα)=0.

解得点C对应的参数为

t1=-2(cosα+sinα).

同理可得点D对应的参数为

t2=2(2cosα-sinα).

即-2(cosα+sinα)=2λ(2cosα-sinα).

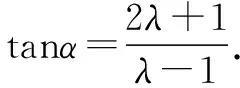
我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休.”由此可见数形结合的重要性，而解析几何的本质就是运用坐标法研究几何问题，因此兼具数与形的特征，所以在解决此类问题时要注重几何直观与方程运算的结合，多角度分析问题、解决问题.

本题的一题多解彰显了数学思维的无限魅力，强调了对知识的融会贯通和方法的灵活运用的重要性，不管是对竞赛学生，还是广大高考学生都大有裨益，特别是在新课标、新高考评价体系的背景下，基于题海战术的刷题应试在高考中已不再有效，更加强调思维的灵活性和知识的综合运用性，而一题多解能够帮助学生们打破思维的定势，锻炼思维的灵活性和认知的深度，进而达到提升学生的核心素养和关键能力的目标. 通过一题多解变式推广，认清了问题的本质，以不变应万变，提高了学习的效率，也是立足“双基”、服务“双减”政策的有效手段.