一道新高考解析几何试题的拓展探究

余业兵

(重庆市西南大学附属中学校 400700)

1 试题呈现

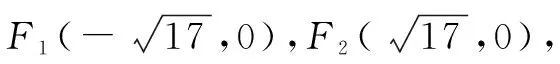
图1

(1)求C的方程.

2 试题解析

由韦达定理，得

又因为|TA|·|TB|=|TP|·|TQ|，

所以k1+k2=0.

故直线AB的斜率与直线PQ的斜率之和为0.

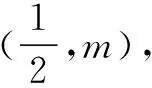
化简整理,得(16cos2θ1-sin2θ1)t2+(16cosθ1-2sinθ1)t-(m2+12)=0.

因为|TA|·|TB|=|TP|·|TQ|，

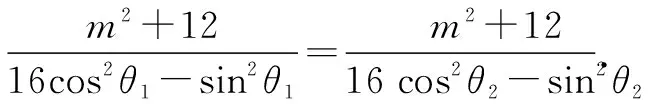
所以cos2θ1=cos2θ2.

所以cosθ1+cosθ2=0.

所以θ1+θ2=π.

故直线AB的斜率与直线PQ的斜率之和为0.

探究1 这里的“斜率之和为零”是一般性规律吗？如果是，它需要满足什么条件？与哪些要素有关系？

证明设直线AB和直线CD相交于点T，若点T在圆外，由圆幂定理知

|TA|·|TB|=|TC|·|TD|.

设点T的坐标为(m,n)，直线AB的倾斜角为θ1，直线CD的倾斜角为θ2.

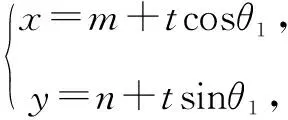
代入b2x2-a2y2=a2b2，得

b2(m+tcosθ1)2-a2(n+tsinθ1)2=a2b2.

整理为(b2cos2θ1-a2sin2θ1)t2+(2mb2cosθ1-2na2sinθ1)t+b2m2-a2n2-a2b2=0.

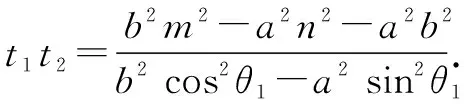
因为A,B,C,D四点共圆，

所以|TA|·|TB|=|TC|·|TD|.

所以cos2θ1=cos2θ2.

所以θ1+θ2=π.

所以kAB+kCD=0.

探究2结论1的逆命题成立吗？即反过来，“kAB+kCD=0”一定有“A,B,C,D四点共圆”吗？

答案是肯定的，我们有如下结论：

证明设点T的坐标为(m,n)，直线AB的斜率为k1，直线CD的斜率为k2,直线AB的方程为y-n=k1(x-m).

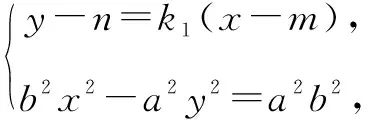
同理可得

因为直线AB和直线CD的斜率为0，

所以|TA|·|TB|=|TC|·|TD|.

由圆幂定理逆定理知，双曲线上四点A,B,C,D四点共圆.

探究3 这个等价命题在椭圆和双曲线中也成立吗？

类似地，大家不难证明以下结论成立.

结论4 一般地，若A,B,C,D是抛物线E:y2=2px(p>0)上的任意四个不同点，若直线AB和直线CD的斜率都存在，则“直线AB和直线CD的斜率之和为0”与“A,B,C,D四点共圆”等价.

就像这道高考试题一样，很多看似普通的数学题目背后常常蕴含了深刻的规律性，对题目的深入思考与探究不仅可以让我们厘清题目背后的逻辑规律、来龙去脉，更可以开阔视野，拓展思维，从而站得更高，看得更明，窥见整个全局.这就是数学探究的魅力所在！