关于教材中一道课后习题的思考

哈尔滨市第一〇七中学 唐 宏

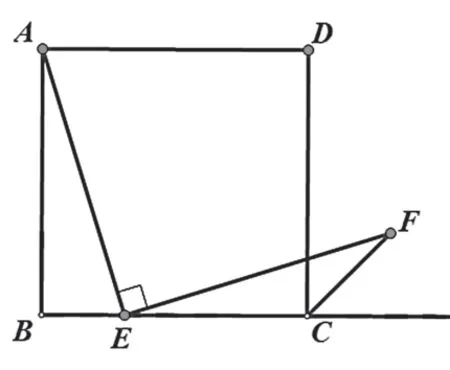
人教版义务教育课程标准实验教科书数学八年级（下册）第二十五章中有这样一道很值得回味的课后习题。原题：如图，四边形ABCD是正方形，点E是BC边的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F，求证：AE=EF.（提示：取AB的中点G，连接EG.）

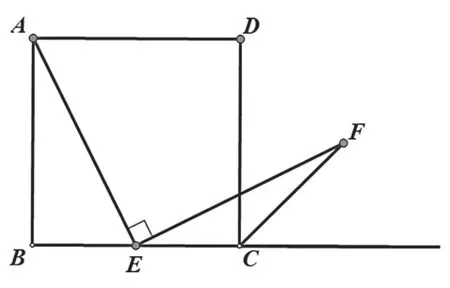
一、问题的分析

这道课后习题是一道非常值得研究的好题，深入研究这个问题能够把初中直线型几何问题发挥得淋漓尽致。教材中的处理大大降低了这道题的难度。第一，教材中给了解决问题的提示，学生根据提示很容易构造两个全等的三角形，从而顺利地得到结论。第二，题目中把点E设置为BC边中点，使问题特殊化，在问题的解决上可能就会用到特殊的方法，如利用计算也可以解决这个问题。

我们发现点E在直线BC上任意位置结论都成立，也就是说这道题并不是静态的数学问题，而是一个动态问题，我们在教学时，可以适当调整，如将点E是BC中点改为点E是BC边上一点，对于知识点掌握好的学生，可以考虑点E为直线BC上一点，分情况探究。或是去掉提示，让学生的思想从束缚中解放出来，充分想象在初中阶段证明两线段相等的方法有哪些，根据这些思维想象，设计解决问题的方法，最后达到解决问题的目的。

在几何证明问题中，最常见的就是证明线段相等或角相等，其方法也是多种多样，这里我们以线段相等为例，研究证明两条线段相等的一些主要思想与方法。

二、问题的提出与解决

例题：如图，四边形ABCD是正方形，点E是BC边上一点，∠AEF=90，且EF交正方形外角的平分线CF于点F.求证：EF=AE.

分析角度一：边等角等构全等

本题中证明线段EF=AE，可以考虑把线段EF、AE放在两个三角形中证全等，但是EF与AE所在的两个三角形不全等，因此可以考虑构造全等三角形。

因为∠CEF=∠BAE，EF=AE，但CE≠AB，可以考虑构全等三角形。

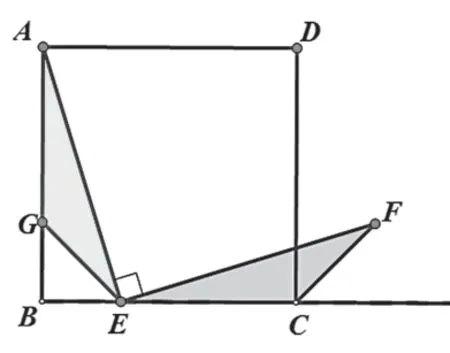
解法1：

在AB上截取AG=EC，

证明△CEF≌△GAE，所以EF=AE.

小结：利用已知条件一组对应角等，截取边相等构造全等三角形。

连接AC可证∠CFE=∠CAE，EF=AE，但CF≠AC，可以考虑构全等三角形。

解法2：保留△CEF，

连接AC，因正方形ABCD，

过点E作EG⊥BC，交AC于G，则∠EGC=∠ECG=45°，

证明△ECF≌△EGA，所以EF=AE.

小结：利用正方形对角线的性质，连接对角线，得到角相等，构造全等三角形。

解法3：保留△ACE，

连接AC，因为正方形ABCD，

过点E作EG⊥BC，交FC延长线于G，

证明△AEC≌△FEG，

所以EF=AE.

小结：利用正方形对角线的性质，连接对角线，利用翻折构造全等三角形。

分析角度二：从图形变换看

本题证明线段EF=AE，可以通过图形变换改变AE或EF的位置，再证明相等，也就是等量代换。

通过对△ABE实施变换来改变AE的位置得到新的线段，证明变换后的线段等于EF。

解法4：对△ABE作翻折变换，

延长FC交AB的延长线于G，

证明△GBE≌△ABE，

所以∠BGE=∠BAE，EG=AE，

因为∠CEF+∠AEB=90°，∠-GAE+∠AEB=90°，

所以∠CEF=∠BAE=∠BGE，

因为∠EGF+∠BGE=45°，∠EFG+∠CEF=45°，

所以∠EGF=∠EFG，

所以EF=EG，所以EF=AE.

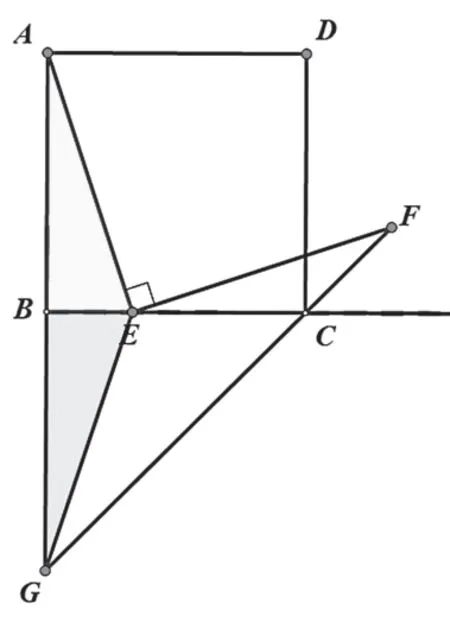
小结：利用等量代换，根据翻折变换把相应线段进行转换。

解法5：对△ABE作旋转变换

因为正方形ABCD，

在AB的延长线上截取BG=BE，连接EG

证明△ABE≌△CBG，

所以AE=CG，∠ECG=∠BAE=∠CEF，

所以EF//CG，所以四边形EGCF是平行四边形，

所以EF=CG，所以EF=AE.

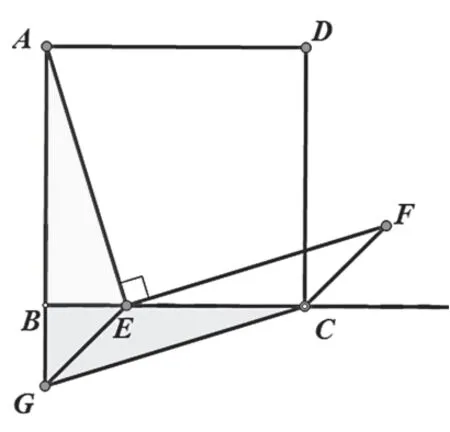
小结：利用等量代换，根据旋转变换把相应线段进行转换。

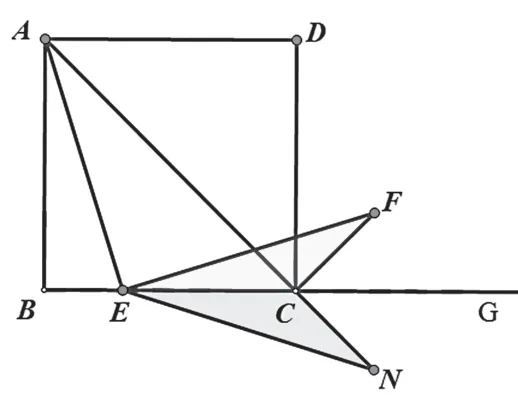
解法6：对△CEF作旋转变换

连接AC，因为正方形ABCD，

在AC上截取CG=CF，

在DC的延长线上截取CN=CE，连接NG、NE，

证明△ECF≌△NCG，

证明四边形AENG为平行四边形，

所以NG=AE，所以EF=AE.

小结：利用等量代换，根据旋转变换把相应线段进行转换。

三、问题的变式训练

（一）题目中的条件结论互换

变式一：如图，四边形ABCD是正方形，点E是BC边上一点，G在BC的延长线上，F在∠DCG的平分线上，且EF=AE.

求证：EF⊥AE.

变式中把原题的已知和结论进行了互换。

解法1：翻折△ACE

延长FC到N，使CN=CA，连接EN，

可证△NCE≌△ACE，

所以∠N=∠CAE，NE=AE，

又 因 为EF=AE， 所 以EF=NE，

所以∠N=∠F，所以∠CAE=∠F，

所以∠AEF=90°，即EF⊥AE.

解法2：翻折△ECF

延长AC到N，使CN=CF，连接EN，

由∠FCE=∠NCE=135°，EC=EC，

则可证△NCE≌△FCE，

所以∠N=∠F，EN=EF，

又EF=AE，所以EN=AE，

所以∠N=∠CAE，所以∠CAE=∠F，

所以∠AEF=90°，即EF⊥AE.

解法3：做双垂构旋转

过点E分别向AC、FC引垂线，垂足为M、N，

易证EM=EN，又AE=EF，

所以△AEM≌△FEN，

所以∠F=∠EAM，

所以∠AEF=90°，即EF⊥AE.

小结：有了上述证明方法，虽然条件和结论互换，仍然很容易想到解决问题的方法。考察了学生们举一反三的数学思维。

（二）条件改为其他等价条件

变式二：如图，四边形ABCD是正方形，点E是BC边上一点，G在BC的延长线上，F在∠DCG的平分线上，且∠EAF=45°.

提示：此问题的主要解法是利用旋转相似，利用旋转相似的成对性解决问题，如下图所示.

原题是教材八年级下册的一道课后习题，教师在讲九年级下册三角形相似时，也可以把这个问题提出来，让学生们思考能不能用相似的知识去解决。学生们会想起自己曾经研究过这个问题，并跃跃欲试地要进行证明。这时候教师应该温馨提醒：一是注意题目中条件的变化，二是应用三角形相似的知识去解决，由此燃起学生们的学习激情。学生们思考过后，能想出用旋转相似解决问题，既用到了图形变换中的相似，又用到了三角形的相似，可以说是一箭双雕。

（三）题目中的E点位置改为在直线BC上

变式三：如图，四边形ABCD是正方形，点E是直线BC上一点，∠AEF=90°，且EF交正方形外角的平分线CF于点F.

求证：EF=AE.

此题证明方法与前面例题方法一致。对于这个问题的变式可以留在习题课上进行讲解，等学生完全掌握了翻折、旋转等图形变换以后，再进行训练，层层深入地把图形变换的思想传授给学生，让他们的能力有一个提升。除此以外，教师还可以进一步做研究，通过加上线段的长度，把问题综合化，这样也更加训练了学生们的思维。

数学题是做不完的，在“双减”的大环境里，教师应该多进行思考，如何在有限的时间里教给学生们无限的方法，同时培养学生们的数学思维。数学课堂教学要在发展学生的思维能力，拓展学生的思维宽度上下功夫。一题多解与问题的变式可以很好地解决这个问题，既培养了学生分析问题的能力，也提升了学生解决问题的能力。将数学问题适当变换条件或者结论，变化形式或内容，会得到一些新的数学题。把一道数学题变成新的数学题，所用知识，解题方法都可能发生变化。通过比较鉴别，会使学生进一步开阔思路，学得灵活；同时有利于巩固基础知识和基本技能的训练，起到举一反三的作用。

问题的变式在新课、复习课和习题课都可以应用。教师可以引导学生从多个角度去分析，让学生们掌握多种方法去解决，同时体会图形变化带来的知识内容上的丰盈；让学生们自己发现数学知识是相通的，在学习的过程中慢慢达到预期的学习目标。

通过这个问题的变式与拓展，希望教师在数学教学的课堂中都能重视变式的应用，利用变式给学生们创造良好的思考氛围和条件，努力达到学生数学核心素养落地的目标。