修磨机格里森弧齿锥齿轮有/无接触模态分析

张启升, 李瑞琴, 梁晶晶

(中北大学机械工程学院， 太原 030051)

螺旋锥齿轮具有传动平稳、承载能力大、噪声低等优点，广泛应用于航空、航天和工程机械传动系统中。磨头是磨床的核心部件，它不仅能承受内齿轮和齿轮箱激振力产生的振动，还要承受工作时钢坯冲击力产生的振动。

磨床磨头采用螺旋锥齿轮传动，齿轮副不仅产生复杂的接触应力，而且在激振力的作用下产生机械振动。当激振力的频率接近齿轮副的固有频率时，会发生共振，产生严重的噪声，甚至齿轮副完全失效。模态分析是分析系统更复杂的动态特性的基础和前提条件。为了更准确地得到系统的动态性能结果，首先要得到符合系统实际情况的模态分布结果。因此，分析弧齿锥齿轮的固有振动特性，找出其在工作状态下的薄弱环节，通过改进结构设计来避免共振的发生具有重要意义。这将提高弧齿锥齿轮的疲劳强度和寿命，具有重要的实际应用价值。

近年来，齿轮是传动系统的核心零件，中外学者针对不同应用场合的齿轮啮合对接触、刚度和动力学等开展了理论和实验研究[1-5]。Hou等[1]基于矢量形式内禀有限元法，推导了8节点六面体单元的计算公式，并将其应用于齿轮的接触分析中。该方法能够精确地分析粗糙啮合模型下的齿轮啮合问题，但是对于精确传动的齿轮力学精度尚待验证，而且该方法通用性不强。刘明勇等[6]利用有限元软件在考虑齿轮啮合时会产生塑性变形、齿面摩擦、温度以及材料线性强化等因素影响，研究了斜齿轮啮合过程中齿面接触力分布。杨博会等[7]利用有限元法分析了不同几何传动误差的齿轮副的接触应力、承载传动误差，得到在特定工况下随着传动误差的增大，边缘接触程度减少。纪红等[8]通过对弧齿锥齿轮齿面进行接触分析，采用磨齿的方法加工齿轮，借助三坐标测齿对弧齿锥齿轮进行加工和检测，对复杂速比的弧齿锥齿轮设计和加工，提供了有效的解决方案。任海果等[9]计算了5个螺旋齿轮在不同腹板厚度下的自振特性，总结了几种基本的低阶模态。Faydor等[10]给出了三齿弧齿锥齿轮有限元接触分析方法。刘坤等[11]为验证高压泵斜齿轮结构的可靠性对轮齿啮合处的受力情况进行静态分析，同时为避免共振的发生进行模态分析,得到系统的振动特性和固有频率通过分析，验证了结构的合理性。李飞等[12]分析了摩擦因数、重合度对传动系统振动幅值的影响。得到不同工况下摩擦因数不同，随着润滑油的变化产生一定的规律。李源等[13]利用有限元软件分析了航空弧齿锥齿轮的啮合过程。栾孝驰等[14]针对某型航空发动机传动锥齿轮在使用中因行波共振造成的从动轮断裂失效问题,采用仿真分析与试验验证相结合的方法，研究弧齿锥齿轮参数调节状态下的行波共振特性及其影响规律。李盛鹏等[15]在考虑转速和传动力矩引起的预应力利用ansys软件对锥齿轮动频率进行了分析，得出离心力和啮合扭矩对弧齿锥齿轮的振动频率有一定的影响。

综上所述，学者们通过实验、理论分析法或有限元方法对齿轮的固有频率和振型进行了大量的研究。但是，鲜见实际工况下动态接触模态分析问题的研究。因此，现针对某钢铁公司磨床的需求，设计了一套磨头齿轮减速器，采用螺旋锥齿轮传动。为了保证模态数据与实际工况的一致性，应建立磨床磨头传动系统的精确模型，并将约束因素作为实际状态施加在齿轮上，在进行模态计算时，接触模态分析将边界条件添加到对象上，如此分析将更接近工程实际情况。利用有限元分析软件研究稳态工况下有、无接触情况下的固有特性和振动模态，为弧齿锥齿轮的疲劳寿命及设计提供可靠的理论依据。

1 动力学方程及接触模态分析理论

在稳定的工作状态下，磨床磨头的应力会影响因负载恒定而产生的固有频率。因此，在进行模态分析时，考虑预应力的影响是很重要的。预应力模态计算的基本过程如下：首先进行线性静力分析，然后考虑随时间变化的荷载，以及质量、阻尼等惯量的影响。

1.1 动力学方程

在经典力学理论中，n自由度系统的结构动力学方程为

(1)

不考虑阻尼效应时，系统将进行自由振动，即C=0，F=0，式(1)与式(2)等价。

(2)

得到特解为

x=φsin(ωt+α)

(3)

式(3)中：φ为自由响应的位移振幅向量矩阵；ω为频率向量；t为时间；α为待定的值。

将式(3)代入式(2)中得到振型方程为

(K-ω2M)φ=0

(4)

式(4)中：ω2为特征值；φ为特征向量。

当φ不为零时，式(4)是一个广义特征值问题。

它也是一个n阶代数齐次数组，以φ的元素为变量，方程非零解的充要条件是其系数矩阵的行列式等于零，即

|K-ω2M|=0

(5)

式(5)称为式(4)特征值问题的特征方程，是关于频率ω2的n次代数方程。当没有相等的根时，得到n个大于零的不同根ω0i(i=1,2，…，n)，即0<ω01<ω02<…<ω0n。其中，ω0i为振动系统的第i阶主频率，为结构的固有频率，为相应的无阻尼振动系统。当将每个ω0i(i=1,2，…，n)代入式(4)，可得含有n-1个关于φi的独立方程的代数数组。然后，得到线性无关的非零向量φi的n个解式(6)。用归一法，得到主振型，这是一个无阻尼的振动系统，因此它是实向量的固有振型。

φi=[φ1i,φ2i,…,φni]T，i=1,2,…,n

(6)

φ=[φ1,φ2,…,φn]

(7)

特征值和特征向量是系统的特征参数，特征向量φi为n维列向量，方程(7)是一个n×n阶矩阵。它是系统的特征向量矩阵，也称为模态矩阵。

1.2 接触模态分析

接触模态是指齿轮传动系统在实际工况下的固有频率和振型分布。由于介质阻尼的存在，齿轮系统的模态与真空和油中的有一定的差异。接触模态分析增加了实际情况的边界条件，结果更接近实际工程情况。

在求解接触模态的过程中，首先进行线性静力分析，然后得到用于结构分析计算的应力刚度矩阵(σ0→S)，最后利用式(8)求解接触模态。

(8)

式(8)中：ω0i为振动频率；φi为模态。

计算固有频率和振型的方法有很多，如矩阵迭代法、子空间迭代法、lanczos法等。Lanczos法，可以快速从复杂模型中提取多阶模态，集成于Ansys中。分析后可以通过图形显示分析和使用结果。

Ansys Workbench中接触模态分析的一般流程和步骤如图1所示。在稳定的工作状态下，磨床磨削头的应力会影响因负载恒定而产生的固有频率。因此，在进行模态分析时，考虑预应力的影响是很重要的。预应力模态计算的基本过程如下:首先进行线性静力分析，然后在第一步的基础上求解结构的固有特性。

图1 接触模态分析过程Fig.1 Process of contact modal analysis

2 格里森螺旋锥齿轮设计与模型建立

为某钢铁企业开发的修磨头传动采用的是格里森弧齿轮，首先必须确定该种复杂齿轮的各种设计参数。

2.1 格里森螺旋锥齿轮副的设计

齿轮由电机驱动，两轮轴交角Σ=90°，大齿轮安装于输入轴一端悬臂支承，小齿轮安装于输出轴两端由轴承支承于箱体上。弧齿锥齿轮的参数非常多，限于本文的篇幅和重点，文中忽略了参数的计算过程，最终确定的齿轮的基本参数设计出二维图(图2)。建立三维图完成装配，如图3所示。

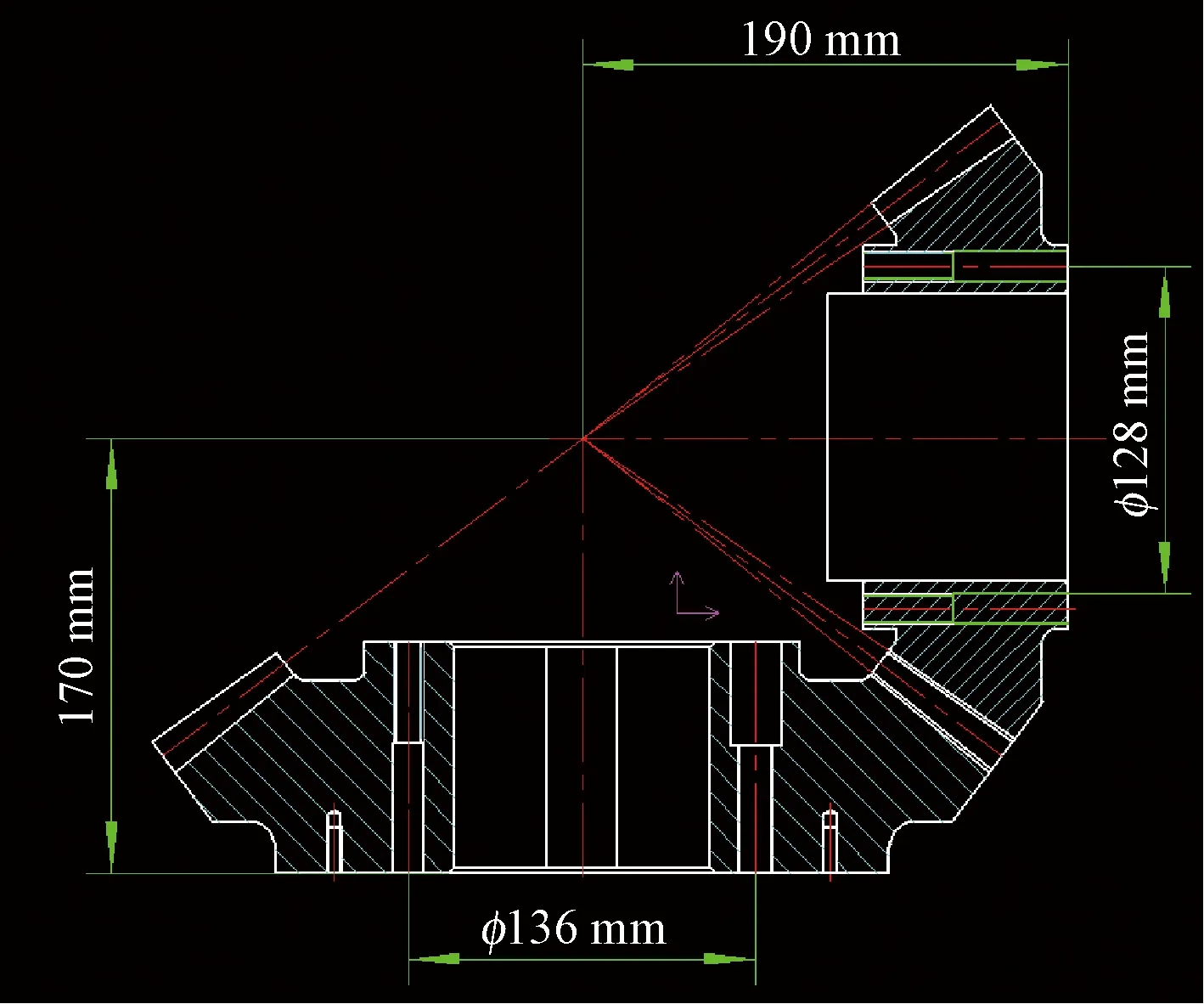
图2 格里森弧齿锥齿轮Fig.2 Gleason spiral bevel gear

图3 格里森弧齿圆锥齿轮实体模Fig.3. Solid model of Gleason spiral bevel gear

2.2 格里森弧齿锥齿轮的实体模型的建立

格里森弧齿轮结构复杂，为了精确模拟齿轮在工作状态下的受力情况，必须建立合适的分析模型，以更接近实际情况。综合考虑计算精度的影响及有限元模型的计算规模，根据圣维南原理，对部分局部特征进行了简化。对齿轮分析而言，模型的简化主要从以下方面着手：①忽略在工作过程中仅起连接作用弧齿锥齿轮与轴连接的键及固定螺栓和孔特征；②忽略主动轮和被动轮端面的螺纹、倒角特征和各处的过渡圆角，将质量进行等效分布。

3 有限元分析前处理过程

3.1 有限元模型的建立

有限元模型建立的几个关键问题包括单元类型的选择、网格尺寸的控制、网格划分密度、单元的阶数等。设置平均单元边长为2 mm，选取网格划分方式为自动划分。齿轮的材料为20CrMnTi弹性模量E=2.07×105MPa，泊松比μ=0.254,材料密度7 830 kg/m3。

3.2 创建接触对

在一定的工作载荷下，使格里森弧齿锥齿轮的接触比保持在合理的范围内，可以使轮齿刚度的变化相对柔和，降低齿轮引起的振动噪声和强度失效的风险。

螺旋锥齿轮在满负荷条件下的接触比计算式为

(9)

式(9)中：εr、εα、εβ分别为总重合度、端面重合度和纵向重合度。

齿轮副的重合度为 2.3，由重合度的要求可知弧齿锥齿轮同时参与啮合的齿对数最多为 3对，因此采取三齿啮合模型进行接触模态分析。齿轮接触采用实体模型为面-面接触。设置三对接触对，其中大齿轮为主动轮作为接触面，小齿轮为被动轮作为目标单元，摩擦系数为0.06。

3.3 约束与加载

文中分别分析齿轮自由模态和接触模态，前者不需要对模型施加任何约束和载荷，而接触模态分析比前者复杂得多。根据实际工作条件，在输入轴上施加2 100 N·m的扭矩，而在主轴上施加890 N·m的阻力扭矩。圆柱约束施加在轴承上，这使得齿轮只能绕轴承的轴线旋转。

4 格里森弧齿锥齿轮模态分析

4.1 无预载荷模态仿真

模态分析主要用于确定格里森齿轮的内在特征，在此基础上可以确定齿轮的设计是否合理，通过优化使齿轮零件满足生产对质量和精度的要求。从软件中得到齿轮自由模态下前10阶固有频率如表1所示。

每一个模态的固有频率对应一个振型图，其中，自由模态分析中前3阶是3个方向的刚体模态，频率都近似为0，仅仅是上下和左右振动没有实际工程意义，故在此忽略。图4为第4～第10阶的振型图，从频率振型图能够得到以下结论：第4～第6阶也为刚体模态，但是他们的数值远远大于0。第4阶，大小齿轮各有一端轴向振动；第5阶，大小齿轮各有一端轴向振动，相似于第4阶；第6阶大齿轮对角轴向振动，小齿轮有一端轴向振动；第7阶模态其实是真实的第一阶模态，大齿轮周向滚动振动,小齿轮左右摇摆振动；第8阶，大齿轮对角轴向振动，小齿轮有一端轴向振动；第9阶，大齿轮周向滚动振动,小齿轮对角轴向振动；第10阶，大齿轮四端轴向振动, 小齿轮周向对折振动。

表1 格里森齿轮自由模态前10阶固有频率

图4 第4 ～ 10阶的自由模态振型图Fig.4 Free mode shape diagram of the 4th～10th order

4.2 齿轮的接触应力分析

在稳定工作状态下得到齿轮的等效应力云图和等效位移云图分别如图5(a)和图5(b)所示。从图5(a)可以看出，最大等效应变发生在从动轮齿面接触处，其值为1.396×103m。图5(b)是两对齿啮合的应力云图；由应力的云图可以看出，应力主要集中在接触部位和齿根，该位置啮合最大应力发生在小齿轮啮入齿的齿根处，最大应力值为311.37 MPa，小于材料的许用接触疲劳应力。图6为大、小齿轮接触考虑摩擦时的总接触应力云图，最大接触应力分别为278.208 MPa 和311.37 MPa。对图6(a)和图6(b)进行比较可知,齿轮副在运转过程中,其接触位置的应力应变最大，齿根应力与接触印痕的移动方向一致，因为接触应力比齿根应力大许多，所以齿根应力显示不明显。

图5 稳定工作状态下等效应力云图和等效位移云图Fig.5 Equivalent stress and equivalent strain under stable working state

4.3 齿轮的接触模态分析

通常情况下，低阶固有频率的振动对结构的动力性能影响很大，而远离振源的模态频率对结构振动的实际贡献很小。因此，在进行满足工程需要的接触模态分析时，通常可以提取系统的前6阶固有频率和相应的振型。

在静力分析的基础上，对螺旋锥齿轮副进行了接触模态分析，得到了相关的频率和振型(表2)和齿轮副的前6阶振型如图7所示。与自由模态分析的结果进行了比较，得出如下结论。

图6 考虑摩擦时的齿轮接触应力云图Fig.6 Contact stress cloud diagram of gear considering friction

表2 弧齿锥齿轮各阶振动特性

图7 工作状态下齿轮副的前6阶振型Fig.7 First 6 vibration modes of gear pair under working state

(1)在预应力状态下，齿轮副的固有频率略有增加，各阶振动模态与未施加预应力时相似。接触模态状态下，对齿轮的动态特性影响不大。第1阶为主动齿轮和被动齿轮的圆周振动和滚动振动，被动齿轮的径向振动和拉伸振动；第2阶是被动齿轮一端上下振动；第3阶是被动齿轮从一侧振动到另一侧；第4阶为被动齿轮振动向相对方向折叠；第5阶是被动齿轮沿4个方向扭转和沿周向折叠振动；第六阶是驱动齿轮在6个端部伸缩振动，被动齿轮在圆周方向振动折叠。

(2)在自由模态下，第7阶和第8阶的频率非常接近，与1阶和2阶频率相当，因此很容易引起共振现象。接触模态时，2阶和3阶频率非常接近，容易发生共振。因此，在进行齿轮设计时，外部激励和啮合内力引起的频率区域应尽量避免以上区域。

(3)系统固有频率与结构刚度矩阵、质量矩阵有关。本文中,载荷对质量矩阵的影响可以忽略，频率随着结构刚度的增大而提高。

(4)通过齿轮回转频率公式fr=n/60和啮合振动频率公式fh=nZ/60，可得出该齿轮内部激励不会使齿轮自身产生剧烈振动。

5 结论

对格里森弧齿锥齿轮进行了自由模态和接触模态分析。对格里森弧齿锥齿轮在稳态工况下的模态进行了分析，得出了齿轮的接触应力和前6阶振型及固有频率，得出以下结论。

(1)对螺旋锥齿轮模型进行了静力学分析，验证了其结构的合理性。弧齿锥齿轮的应力和变形主要集中在接触区，其次是齿根区的受压侧和受拉侧，齿根裂纹后，有裂纹时的最大位移大于无裂纹时的最大位移；小裂纹对接触应力影响不大，切削刃应力集中导致齿根应力值突变，裂纹尖端附近的应力值比无裂纹时大。传动开始啮合时，齿轮啮合的最大应力出现在轮齿根部。弧齿锥齿轮副的接触比大，前端承载三个齿，微小裂纹对应力值影响不大。

(2)分析了接触工况的齿轮系统固有频率和振动模型。与自由模态分析相比，外载荷不是影响模态的关键因素，但其影响不容忽视。固有频率随结构刚度的增加而增加。接触模态的一阶频率为389.2 Hz，高于弧齿锥齿轮的稳态工作频率，因此不会出现共振现象，弧齿锥齿轮的设计具有较好的动态特性。模态分析结果弧齿锥齿轮动力学的结构设计和进一步研究提供了理论依据，同时也为齿轮的结构优化和噪声控制提供了参考依据。