一种基于CSF-WOA-LSSVM的匹配点云土石方量计算方法
2022-12-05何广焕唐诗华王文贯张炎刘银涛蒙金龙
何广焕, 唐诗华*, 王文贯, 张炎, 刘银涛, 蒙金龙
(1.桂林理工大学测绘地理信息学院, 桂林 541006; 2.广西空间信息与测绘重点实验室, 桂林 541006;3.广西建设职业技术学院土木工程学院, 南宁 530007)
土石方量计算在工程施工项目、国土资源监测中占据着不可忽视地位,其计算结果的准确性是工程项目的施工进度、造价预算以及土地资源储备量估算的重要影响因素[1],如何准确高效地计算土石方量已成为当今众多学者的研究方向。无人机倾斜摄影测量技术可快速获取测区影像匹配密集点云,进而可利用密集点云建立数字高程模型或提取地面点进行土石方量计算[2-3]。当前,诸多学者将无人机倾斜摄影测量技术应用在土石方量计算上已取得一些阶段性的研究成果。李博等[4]提出利用Photoscan软件对无人机影像进行匹配密集点云生成,然后对通过点云分类和非地面点高程修正法生成的数字高程模型进行土石方量计算,高效、准确地获取了土石方量计算成果。相诗尧等[5]利用五镜头影像对公路建立实景三维模型,通过重新构建模型表面三角网来剔除植被、房屋、树木等影响土方计算的地物,并利用清表后的实景三维模型生成地面点云,进而计算公路土石方量。高利敏等[6]通过匹配点云生成两期DEM模型,结合Virtual Surveyor软件计算土方变化量,为土方监测提供了一种新方法。王春香等[7]利用改进的神经网络对三维点云模型空洞进行修复,很好地还原了三维点云模型的真实性。李雅盟等[8]运用布料模拟滤波(cloth simulation filtering,CSF)法对激光点云进行地面点提取,通过设置相应的地形阈值取得了很好的效果。刑鹏威等[9]通过不规则三角网法对匹配密集点云进行地面点云提取,并利用最小二乘支持向量机(least squares support vector machine,LSSVM)对地面点云空洞进行修复,获得了稳定、可靠的地面点云。
现有的研究已很好地促进了无人机倾斜摄影测量技术在土石方量计算中的应用与发展,但直接通过匹配密集点云计算土石方量的研究比较少,目前数字正射影像图、数字高程模型、实景三维模型等低空摄影测量产品的成果质量均依赖于匹配密集点云的三维点位精度,由此可看出,匹配密集点云在精度上具有更大的优势[10-11]。为了进一步促进无人机匹配点云在土方计算工作中的作业效率和成果精度,现提出通过CSF滤波法对匹配密集点云进行滤波、降噪、抽稀等处理提取地面点,然后利用经鲸鱼优化算法(whale optimization algorithm,WOA)优化后LSSVM对所提取的地面点空洞进行插值修复,并将修复完成的地面点数据导入南方CASS软件中进行土石方量计算,进而为土方工程提供一种更为快速、精度更为可靠的土方计算方法。
1 土石方量计算流程和算法原理
1.1 土石方量计算流程
为了高效、准确地采集土石方测区的地面点数据,利用无人机倾斜摄影测量技术、PPK技术、RTK技术对测区进行影像、控制点、基站卫星观测文件等数据采集。利用Photoscan、PEN-PPK软件对采集完成的数据进行处理生成匹配密集点云,对匹配密集点云进行CSF点云滤波、WOA-LSSVM地面点插值修复,进而获取测区真实地面点数据,最后将处理完成的地面点数据导入南方CASS软件进行土石方量计算。具体流程如图1所示。

图1 土石方量计算流程Fig.1 Calculation process of earthwork volume
1.2 CSF点云滤波原理
传统分离地面点和非地面的滤波算法,大多数是依赖坡度、高程等变化因素来提取地面点,但需要用户对点云数据具有丰富的先验知识才能很好地设置滤波器中的各种参数。Zhang等[12]提出了一种CSF滤波法,该方法先把测区点云进行180°转置,然后将一块网格状构成的布料贴附在转置的地形点云上,布料在重力、邻近节点作用力的相互拉伸下产生位移,当布料静止时,所覆盖的区域就代表当前测区的地形,如图2所示。

图2 布料模拟滤波基本原理Fig.2 Basic principles of cloth simulation filtering
具体表达公式为

(1)
式(1)中:m为粒子的重量,一般定义为1;X为粒子在时间t时的位置;Fext(X,t)为粒子受到的重力大小;Fint(X,t)为粒子受到邻近节点作用力大小。重力和节点相互作用力随时间 变化而变化,所以可用数值积分来求解。
1.3 LSSVM点云空洞插值修复模型
支持向量机属于深度学习中的线性回归法,通过训练学习利用所有的支持向量得出最优分割平面,但在对偶问题上容易出现二次规划现象,为克服其缺点,LSSVM利用最小二乘法将原不等式约束改为等式约束,化简了计算流程,提高了原算法的泛化能力和收敛速度[13-14],能让支持向量机更适用于样本多、面积大的点云空洞修复。其原理及修复过程如下。
给定点云训练样本集{(x1,y1),(x2,y2),…, (xn,yn)}, 则xn∈Rn表示高程点的平面二维坐标,yn∈Rn为高程一维输出样本。利用映射函数φ(x)把输入的三维地面点数据映射到高维特征空间,并在该空间中构造优化的线性回归函数,其数学模型为
y(x)=wTφ(x)+b
(2)
式(2)中:y(x)为高程预测值;wT式为训练权重向量;b为偏差值。根据结构风险最小化原则,将其转化为以下优化问题:
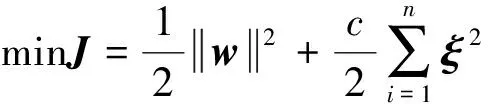
(3)
约束条件为
s.t.yi=wTφ(xi)+b+ξi,i=1,2,…,n
(4)
式中:c为正则化参数,其作用是为了控制地面点云模型的拟合度;ξ为惩罚变量,表示地面点云模型的拟合误差允许值。通过拉格朗日函数和KKT条件优化,可得地面点空洞修复模型为

(5)
式(5)中:ai为拉格朗日乘子,其作用是为找到模型最优解;K(x,xi)为核函数,主要作用是减少计算量。根据Mercer条件,利用径向基函数(RBF)作为地面点空洞修复模型的核函数,具体表达式为
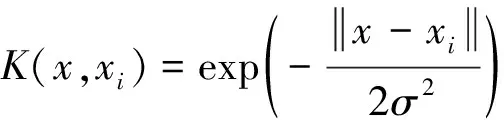
(6)
式(6)中:σ为核函数参数;exp(·)为高斯核函数。
1.4 鲸鱼优化算法
钟明辉等[15]受鲸鱼群捕食行为的启发,提出了一种鲸鱼优化算法。WOA通过模仿鲸鱼对猎物的3种捕猎方式,以达到搜索猎物位置最优解的目的。该算法结构简易,并且在收敛速度、全局寻优能力方面具有一定的优势,其主要作用是为LSSVM点云插值模型提供可靠的正则化参数c和核函数参数σ,进而更好地修复地面空洞点。
1.4.1 环绕猎物
鲸鱼环绕猎物过程中,座头鲸的位置看作待优化问题的解,当座头鲸确定猎物位置后,靠近猎物,并将其位置当作猎物位置,其他鲸鱼不断更新自己的位置并向座头鲸位置靠近,形成环绕猎物的状态,具体公式为
D=|C·X*(d)-X(d)|
(7)
X(d+1)=X*(d)-A·D
(8)
式中:·表示逐元素乘法运算;D为座头鲸与猎物的距离参数向量;d为当前迭代数;X*(d)为猎物位置向量;X(d)为座头鲸的位置向量;X(d+1)为其他鲸鱼群的位置向量;C和A为两个控制参数。
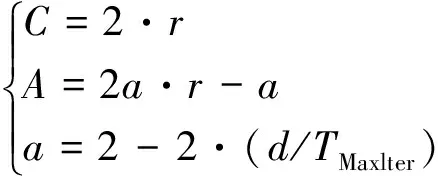
(9)
式(9)中:·表示逐元素乘法运算;r为[0,1]内的随机数;TMaxlter为种群最大迭代次数;a随鲸鱼种群迭代次数的增加从2~0线性递减。
1.4.2 螺旋气泡攻击
鲸鱼进行螺旋气泡攻击时,先计算自身到猎物位置的距离并慢慢逼近,当到达猎物位置对其进行螺旋气泡攻击,具体公式为
D′=|X*(d)-X(d)|
(10)
X(d+1)=D′·ebl·cos(2πl)+X*(d)
(11)
式中:D′为当前鲸鱼与猎物的距离参数;b为1的螺旋状常数;l为[-1,-2]内的随机数。
1.4.3 全局搜索猎物
为了避免鲸鱼在捕食猎物的过程中出现局部最优解的情况,鲸鱼群可通过全局随机搜索的方式实现捕食,根据猎物位置的变化而不断更新自身位置,具体公式为
D=|C·Xrand-X(d)|
(12)
X(d+1)=Xrand-A·D
(13)
式中:Xrand为当前随机猎物的位置。
2 工程实例
2.1 测区概况
本工程为广西陆川县某花岗岩石矿场的土石方量测量项目,测区南北长约480 m,东西宽约550 m,地形相对高差约为110 m,占地面积约为200亩(1亩=667 m2),大部分区域地表呈裸露状态。测区内部含有部分建筑物、棚房、灌木等地物以及石矿生产线中的大型设备。为验证文章土石方计算方法的可行性,均匀选取16个被地物遮挡的隐蔽高程点作为检查点,并通过RTK技术获取其坐标信息。测区及检查点点位分布的具体情况如图3所示。
2.2 数据采集与预处理
2.2.1 数据采集
利用大疆精灵4RTK单镜头无人机对测区进行影像数据采集,根据对测区现场的踏勘情况同时结合飞行设备的硬件参数,采用倾斜摄影3D技术、PPK定位技术、RTK定位技术对测区进行数据采集,共获取测区743张相片、5个点位分布均匀的像控点、1个基站架设点的静态数据及其厘米级的三维坐标。其中航线设计的具体参数为:相对航高为80 m、地面分辨率为2.1 cm、飞行速度为7.1 m/s、航向和旁向重叠度为80%、云台角度为-60°。像控点及基站点坐标信息通过RTK技术获取,并对基站点进行静态数据采集,为后期影像POS数据解算提供卫星观测数据。
2.2.2 数据预处理
数据预处理的主要目的是获取测区可靠的匹配密集点云,为后期点云滤波、地面空洞插值修复、土石方量计算提供准确的原始点云数据。首先,利用PEN-PPK软件对导入的原始影像POS数据、静态观测数据、厘米级基站点坐标进行联合解算,进而获取高精度的影像POS数据。其次,将准确的POS数据、倾斜相片、像控点导入Photoscan软件进行相对定向、绝对定向、空三加密等处理,进而生成精度可靠的匹配密集点云,具体情况如图4所示。

图4 匹配密集点云Fig.4 Match dense point cloud
2.3 CSF点云滤波降噪
匹配密集点云往往含有许多噪声点,除了地面点云之外,还含有建筑物、植被、湖泊、路灯等非地面点云。本文研究利用CSF滤波法对测区提取地面点云,该算法只需要设置4个参数:时间步长为0.65 s,地面点阈值为0.2 m、格网分辨率为0.2 m、迭代次数为300次。其中,时间步长指布料粒子位置更新所需要的时间;地面点阈值指将具离地面有一定高度的离散点判断为地面点;网格分辨率指布料网格大小,一般设置为点云分辨率的2~3倍。经CSF滤波提取的地面点云如图5所示。

图5 具有空洞的地面点云Fig.5 Ground point cloud with cavity
2.4 地面点空洞修复
2.4.1 WOA-LSSVM插值
通过CSF滤波提取的地面点云,基本剔除了建筑物、植被、大型设备等非地面点云,同时也造成了部分区域产生地面空洞,直接利用该点云数据进行方量计算会使计算结果远偏离土石方量真实值,所以需对地面点云空洞进行修复,尽可能还原地表真实地形。采用WOA-LSSVM对地面点空洞进行插值修复,并且与LSSVM、Kriging插值法以及RTK实测数据进行比较分析。由于点云数据量巨大,且为了提高软件的计算速度,则在修复之前先对提取的地面点云进行抽稀,获取平均间距为3 m的地面点。在WOA算法优化参数的过程中,将LSSVM插值修复模型的点位中误差作为猎物位置更新的适应度函数,鲸鱼种群数量设置为60头,最大迭代次数为100,螺旋状常数设置为1,为LSSVM插值修复模型提供该研究区域最合适的正则化参数和核函数参数。最后把待插修复点的平面坐标导入训练完成的三维点云拟合模型中进行高程预测。图6为经WOA-LSSVM修复后地面点三维模型。

图6 修复后的地面三维模型Fig.6 Repaired 3D ground model
2.4.2 插值修复模型精度分析
由于测区高差过大,并且存在多处高陡崖,所以绘制了全测区的3 m等值线图和局部测区1 m等值线图来验证经WOA-LSSVM插值修复后的地面点可靠性,并且与LSSVM插值法、Kriging插值法以及通过RTK技术按5 m采样间隔获取的实测数据做对比分析,如图7和图8所示。
由图7可知,相比RTK实测数据的3 m等值线图,LSSVM插值法、Kriging插值法存在少量等值线局部突变的情况,并且Kriging插值法在测区中部出现等值线分层,表明两种方法所插值修复的地面点数据存在的离散误差点较多。由图8可知,相比RTK实测数据的1 m等值线图,Kriging插值法、LSSVM插值法在局部测区的左下方出现大范围等值线突起,并且在许多地方出现大小不一的等值线突变,表明存在许多面状区域性的地面点粗差。而WOA-LSSVM修复法在两种等值线图则几乎没有出现等值线分层、突起、变异的情况,并且等值线的走向与RTK实测数据的等值线图更为贴近,表明该方法具有一定的可靠性和稳定性。为了进一步验证WOA-LSSVM插值修复法的精确性,选取16个被地物遮挡的高程点作为检查点,进行精度统计分析,结果如表1所示。
由表1可知,WOA-LSSVM插值法的检查点残差变化区间为-0.317~0.214 m,LSSVM插值法为-0.344~0.224 m,Kriging插值法为-0.519~0.449 m。在整体精度上,WOA-LSSVM插值法的平均误差和中误差分别为:0.105 m和0.137 m,LSSVM插值法为:0.148 m和0.172 m,Kriging插值法为:0.135 m和0.205 m。相较于其他两种方法,经WOA优化后的LSSVM插值法的检查点残差变化区间最小、效果更好,在精度方面也更具优越性。为了更为清晰直观地展现三种插值修复法的变化趋势和稳定性,绘制了检查点残差的变化折线图,结果如图9所示。

图7 4种方法的全测区3 m等值线图Fig.7 3 m contour map of the whole survey area by four methods
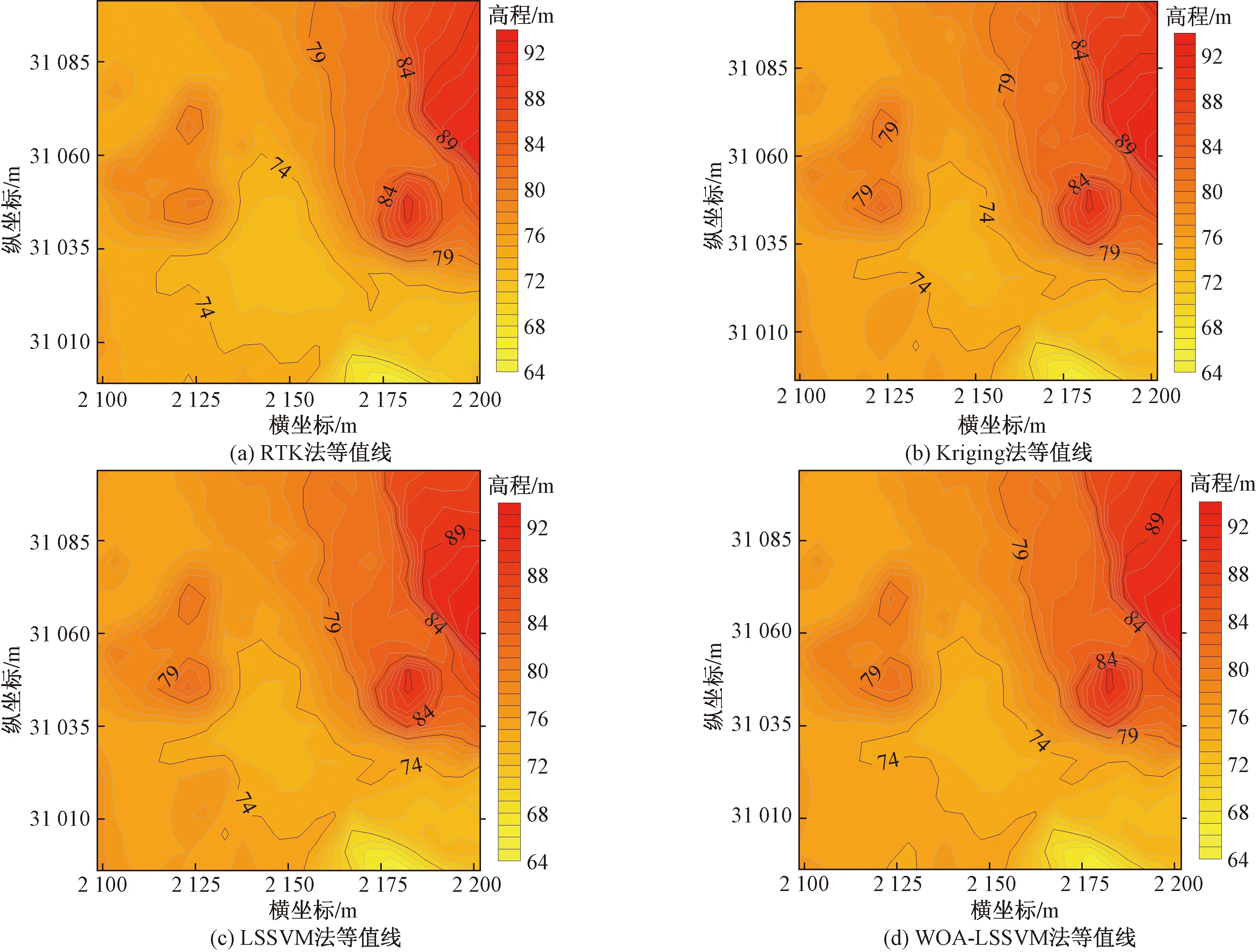
图8 4种方法的局部区域1 m等值线图Fig.8 Local 1 m contour map of four methods

表1 3种修复法的检查点精度统计表Table 1 Statistical table of checkpoint accuracy of three repair methods
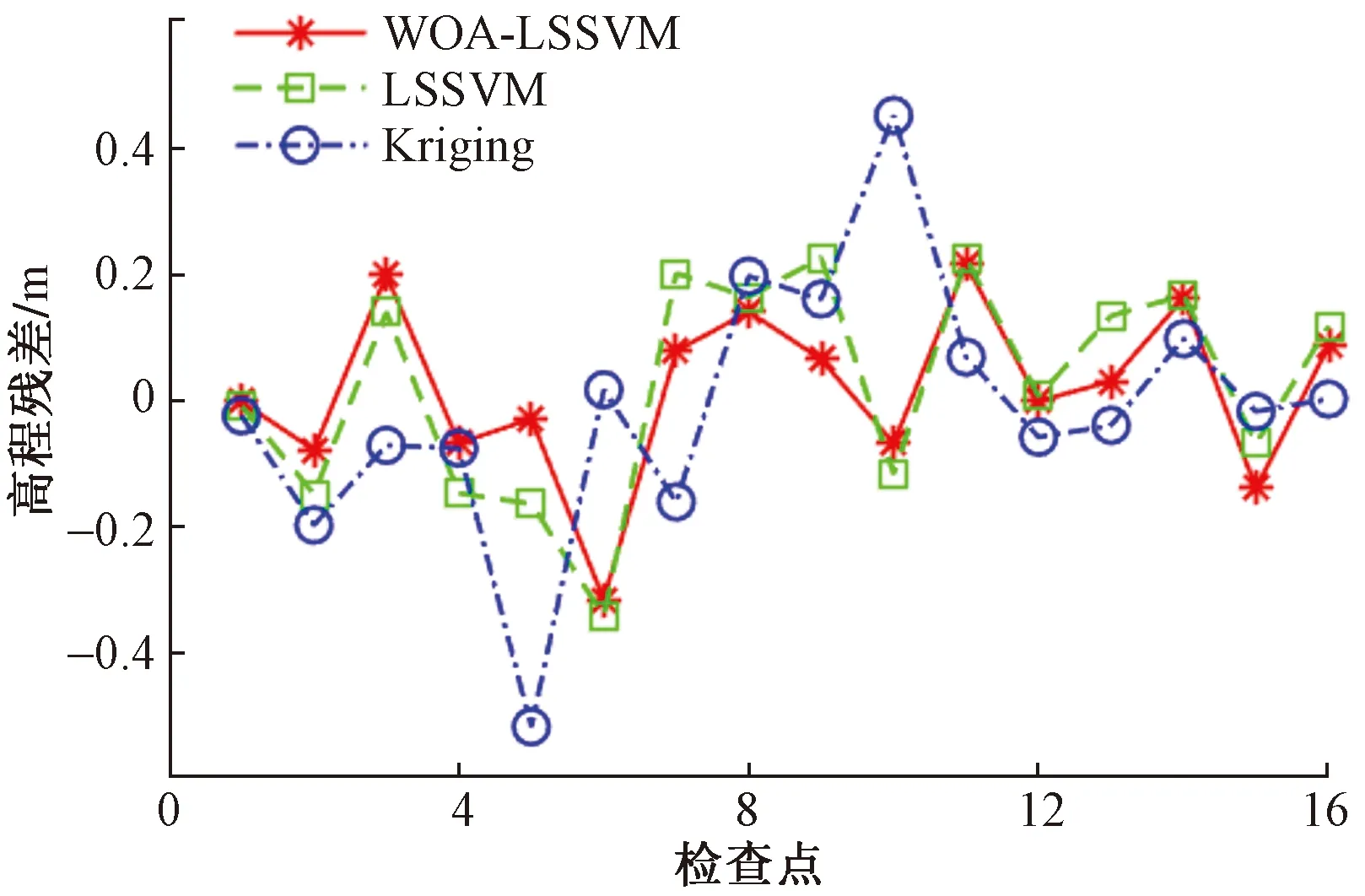
图9 检查点残差对比图Fig.9 Comparison diagram of checkpoint residuals
由图9中的高程残差波动趋势可知,相对于LSSVM插值法、WOA-LSSVM插值法,利用Kriging插值法修复的检查点高程残差波动范围明显更大,而经过WOA优化的LSSVM插值法所修复的隐蔽点高程残差相比原插值方法更为稳定、波动性更小、更趋近于真值。
2.5 土石方量计算
为验证本文方法在土石方量计算中的准确性和可靠性,利用RTK技术按5 m间隔对测区进行地面点数据采集,并在研究区植被较茂密、地势起伏大的区域进行适当的地面点加密采集,然后将CSF-WOA-LSSVM法、CSF-LSSVM法、CSF-Kriging法、RTK技术所处理和实测的地面点数据导入南方CASS软件中,设置相同的标高及相关参数,以及确定相同的区域边界线,通过方格网法计算测区的土石方量,结果如表2所示。
通过对4种方法所计算的土石方量结果进行分析比较可知:
(1)通过对无人机匹配点云进行滤波、空洞插值修复所完成的土方计算工作,在工作效率方面要比传统RTK土石方测量更具优越性,将工作时长缩短了近3倍,并且大大减少了外业工作时间。
(2)与通过传统RTK技术实测计算所获取的土石方量结果相比,经过滤波、插值的3种方法均能满足土石方量计算的规范要求,其中CSF-Kriging法的土石方量和差值比分别为:98 437.4 m3和2.03%;CSF-LSSVM法为90 150.2 m3和1.86%;CSF-WOA-LSSVM法为:67 073.6 m3和1.38%,并且在3种方法中准确性最高,更适用于在土方工程。
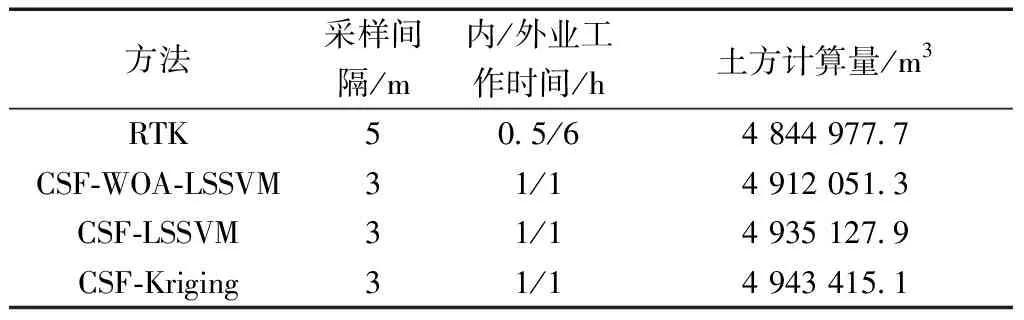
表2 土方计算结果对比Table 2 Comparison of earthwork calculation results
(3)利用WOA-LSSVM插值法修复的地面点数据进行在土石方量计算,所计算的结果相比LSSVM插值法的准确性提高了26%,这主要是因为WOA算法为LSSVM插值法提供了更为准确的正则化参数和核函数参数,从而提高了土石方量计算的准确性。
3 结论
在土石方工程中,如何快速、准确地计算土石方量,对整个项目的施工进度和成本控制具有重要影响。利用无人机摄影测量技术生成研究区的匹配点云,通过CSF滤波法对其进行地面点提取,利用WOA-LSSVM插值法、LSSVM插值法、Kriging插值法对所提取的地面点空洞进行修复,最后将3组插值修复完成的地面点导入南方CASS软件进行土石方量计算,并结合RTK实测土方数据对3种方法进行了精度验证和适用性分析,得出以下结论:①利用无人机影像匹配点云进行土石方量计算,得益于其不受研究区域环境障碍的影响,使得外业数据采集的时间大大缩短,进而有效地提高了工作效率;②CSF滤波算法整体参数设置简单,处理过程中无需过多的先验性知识,并且可较好地提取匹配点云中的地面点;③对具有孔洞的匹配地面点云,利用WOA-LSSVM插值法对其进行修复可获得到稳定、可靠的完整地面匹配点云,具体精度达到了0.137 m;④将WOA-LSSVM插值法所修复完成的地面匹配点云用于土石方量计算,与RTK技术获取的土石方量计算结果相比更为接近,差值比为1.38%,完全满足土方计算的规范要求,可为土石方工程提供一定的参考依据。
