地基附加应力改进计算方法及其规律分析

贺 敏，仰宗宝，徐卓君，曹文贵，张 超，徐 赞

（1.湖南工业大学 土木工程学院，湖南 株洲 412007；2.湖南大学 岩土工程研究所，湖南 长沙 410082；3.湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室，湖南 湘潭 411201；4.湖南城市学院 土木工程学院，湖南 益阳 413000）

0 引言

地基在外荷载作用下的应力分布是基础工程设计的重要依据[1]。目前，工程中普遍运用弹性力学理论[2-4]计算地基土体的附加应力，该方法假定地基土体是均匀和各向同性的弹性介质体。然而实际上地基土体并非连续弹性介质体，而是由若干大小相差悬殊的细小颗粒堆积而成的碎散体，其工程力学性质更加接近于散体介质[5-6]。可见，建立考虑土体散体特征的地基附加应力解析方法是岩土工程亟待解决的关键问题，这正是本文研究的出发点。

目前，基于弹性力学理论的附加应力解析解（Boussinesq 解[2]、Mindlin 解[3]、Flamant 解[4]等）在工程中应用广泛，而针对不同的工程环境和外荷载条件，国内外学者们在经典附加应力解析解的基础上进行了适当的改进，并建立了梯形荷载[7]、轴对称山体荷载[8]作用下，路基[9-10]、桥头[11]等工程背景下，地基土体内部的任意一点[12]等，可应用于不同工况的地基附加应力解析解，但经典的解析方法及其改进解析方法的研究，均是以地基土体为连续均匀弹性体为假设前提的。

众多学者认为，土体是由大量土石颗粒组成的散粒集合体，其应力传递机理、响应机制以及分布规律等均与连续弹性介质不同，于是，一些考虑土体散体介质特征的附加应力解析方法应运而生。学者们采用试验探究[13-17]、离散元数值模拟[18-20]等多种方法对地基附加应力传递及其分布规律进行了探讨，并且进一步研究了其理论解析方法[21-24]，这为工程应用提供了有力的依据。

韦珊珊[13]采用声波测试技术、刘源等[14]采用光弹试验、J.M.Erikson[15]、蒋红英等[16]采用压痕试验、Wang C.D.等[17]采用模型试验，分别探究了散体介质在竖向静荷载作用下的附加应力传递机理及分布规律，均认为散体介质附加应力传递的扩散范围比连续介质（外荷载作用下附加应力扩散范围为半无限空间）的要窄小；C.Goldenberg 等[18-20]采用离散元数值模拟，探究了散体介质在外荷载作用下的应力响应机制，均认为散体介质在外荷载作用下的应力是通过颗粒间的接触和相互作用而向下扩散传递的，散体介质内部形成了明显强弱有别的力链，且其应力扩散范围为以荷载作用域为顶面的锥体；此外，代志宏等[21]考虑颗粒粒径、胶结力、静水压力等因素对土颗粒单独进行受力分析，建立了附加应力分析的细观模型；蒋红英等[22]引入概率理论，建立了二维有序散体介质的附加应力传递模型；廖智强等[23]考虑土颗粒无序排列的复杂性，建立了地基附加应力的概率论解析解；曹文贵等[24]将附加应力传递范围视为半无限锥体，推导了竖向圆形均布荷载作用下的地基土附加应力解析解。

上述关于散体颗粒介质的附加应力传递及其分布规律的研究，为地基附加应力解析方法的进一步发展指明了方向。因此，贺敏[20]在已有研究的基础上，考虑了土体颗粒的力学性质、外荷载大小等因素，对地基土附加应力传递机理及其分布规律展开了初步研究，提出了考虑散体特征的地基土附加应力解析方法。然而，该方法建立的竖向矩形均布荷载作用下的地基附加应力二维积分隐式解，不便被应用于工程实践中，因此，本文拟在此研究的基础上，考虑地基土体的散体介质特征，建立基于Boussinesq解的竖向矩形均布荷载作用下，地基附加应力的改进计算方法，并且对此进行参数分析，以进一步探究地基土附加应力的分布规律。

1 竖向均布荷载作用下的附加应力二维积分表达式

竖向均布荷载作用下，考虑散体介质特征的地基附加应力二维积分隐式解析解参见文献[20]。

1.1 附加应力响应范围的边界分析模型

通过PFC（particle flow code）数值模拟分析，综合考虑土颗粒大小级配、土颗粒相互作用及外加荷载等因素，分析各因素对地基附加应力响应的影响规律，建立如图1 所示竖向均布荷载作用下附加应力响应范围的边界分析模型。

竖向均布荷载作用下地基附加应力响应范围边界分析模型，采用边界曲线上某点到荷载作用域边缘的水平距离Δr来描述，其计算式如下：

式中：z为双曲线上某点到荷载作用域边缘的竖向距离（m）；φ为土体内摩擦角（rad）；q为均布荷载（MPa）；Cu为土体颗粒不均匀系数；βi（i=0,1,…,9）为参数，其取值如表1 所示[20]。

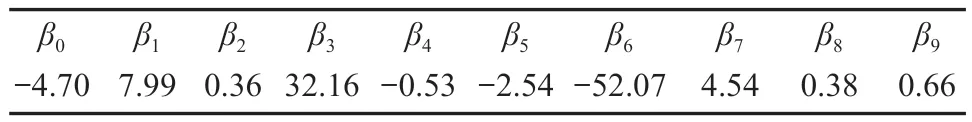
表1 边界分析模型参数取值Table 1 Parameter values of boundary analysis model

1.2 集中荷载作用下的附加应力

将附加应力响应范围内的土体视为整体，引入Love 位移函数，用弹性力学方法推导，得竖向集中荷载下地基附加应力分量解析解如式（2）所示。

式中：σx、σy分别为附加应力所求点M的x、y方向的水平正应力；σz为附加应力所求点M的竖向正应力；F为集中荷载；(x，y，z) 为所求点M的坐标；μ为土体泊松比；

1.3 竖向均布荷载作用下的附加应力

基于应力叠加原理，将竖向均布荷载作用域划分为若干微元，视微元上的荷载为集中荷载，将若干集中荷载在点M处所产生的应力叠加，即为均布荷载在点M处所产生的附加应力。以最常见的矩形均布荷载为例，以矩形荷载作用域的任一角点为坐标原点，建立直角坐标系，对集中荷载作用下的地基附加应力在荷载作用域内进行面积积分，如图2 所示，即可得到竖向矩形均布荷载作用下附加应力分量二维积分表达式，如式（7）所示。

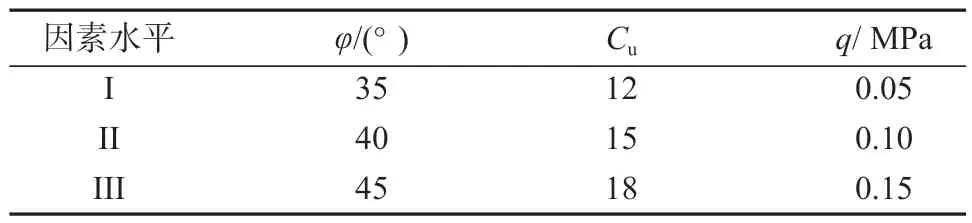
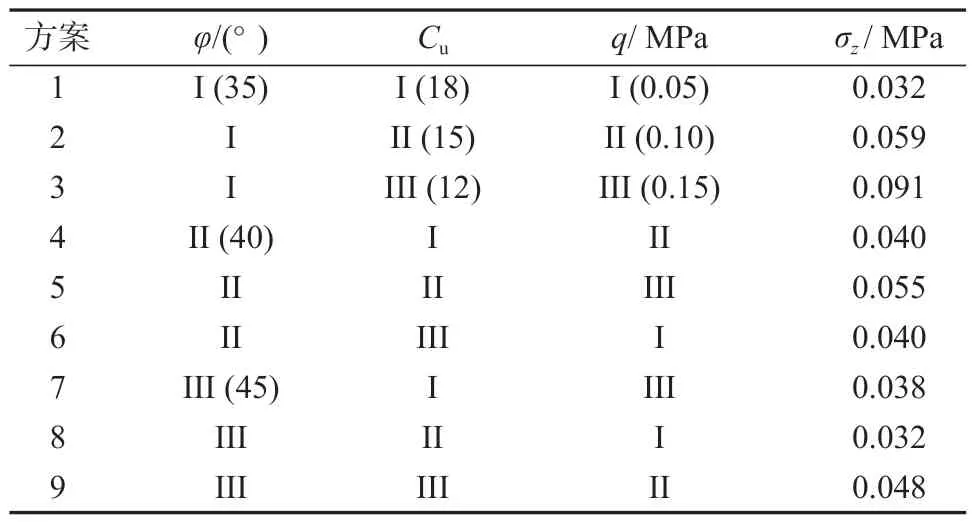
式中：l为荷载作用域长；b为荷载作用域宽；qdξdη为微元集中力dF，其中，0<ξ

2 竖向矩形均布荷载作用角点下的附加应力解析解

为便于积分，取竖向矩形均布荷载作用域角点下M点（位于直角坐标系z轴上），则x=0，y=0，代入式（7）和（8），可得下面以水平附加应力和竖向附加应力为例，推导二维积分表达式的附加应力显式解析解。

2.1 水平附加应力分量的推导

对η积分并整理后，得式如下：

令ξ=g(z)tant，dξ=g(z)sec2tdt，代入式（14）并整理后，可得：

对β和ξ积分并整理后，可得：

令m=l/b，n=g(z)/b，代入式（17）并整理后，可得：

式（18）即为考虑散体特征的竖向矩形均布荷载作用角点下水平附加应力分量的显式表达式。

2.2 竖向附加应力分量的推导

式（12）中，竖向附加应力σz经过整合后，其表达式如下：

对ξ积分并整理后，可得：

令η=g(z)tant，dη=g(z)sec2tdt，代入式（20）并整理后，可得：

令β=sint，dβ=costdt，cos2t=1-β2，代入式（21）并整理后，可得：

对β积分并整理后，可得：

令m=l/b、n=g(z)/b，代入式（23）并整理后，可得：

式（24）即为考虑散体特征的竖向矩形均布荷载作用时，角点下竖向附加应力分量的显式表达式。

2.3 附加应力的解析解表达式

由上述公式推导可知，竖向矩形均布荷载作用时，角点下竖向附加应力的解析解如下：

式中：m=l/b；n=g(z)/b；g(z)见式（1）与式（3）；Δt见式（10）；Δk见式（11）。

式（25）即为考虑散体特征的竖向矩形均布荷载作用时角点下附加应力的解析解。

3 显式解析解的合理性验证

本研究是在考虑散体特征的地基附加应力隐式解析解[20]的基础上，推导得到的显式解析解（见上文中式（25））。而且文献[20]采用室内模型试验和PFC 颗粒流数值模拟试验，已经对隐式解的合理性和适用性进行了验证。研究结果表明：文献[20]的方法与Boussinesq 解相比更接近试验监测值，这是由于Boussinesq 解将地基土体视为半无限的线弹性连续介质，未考虑地基土物理力学参数以及荷载大小对附加应力响应范围的影响，而文献[20]的方法将地基土体视为散体介质，考虑了土体物理力学参数对附加应力响应范围及其解析解的影响，理论上更加符合实际情况。

下面将对比分析本文推导得到的显式解析解（见式（25））与文献[20]中隐式解（见式（12））以及Boussinesq 解，在竖向矩形均布荷载中心线上的竖向附加应力σz的计算结果，以验证本文显式解析解的合理性和可行性。

由于式（25）为竖向矩形均布荷载角点下附加应力的解析解，因此，需采用“角点法”确定矩形均布荷载中心线上的竖向附加应力σz。本研究中将矩形均布荷载划分为4 个小矩形，计算一个小矩形在角点下产生的附加应力，再乘以4 即可得到矩形的竖向附加应力值。文献[20]中的模型试验参数设置如下：荷载作用域的尺寸l×b为0.3 m×0.3 m，泊松比μ为0.2，内摩擦角φ为35°，颗粒不均匀系数Cu为10，所求点埋深z分别为0,0.25,0.50,0.75,1.00 m，均布荷载大小分别为50,100 kPa。据此参数，按式（25）、文献[20]中隐式解和Boussinesq 解分别计算矩形均布荷载中心线上的竖向附加应力σz，所得结果如图3所示。

由图3 可以得知，以本文推导得到的竖向矩形均布荷载作用下地基附加应力改进解析方法计算得到的附加应力随深度的分布形态，与Boussinesq 解计算得到的分布形态基本相同，即在荷载中心线上的附加应力均随着深度的增加而逐渐递减。由此可知，本文推导的显式解析解合理且可行，是一种考虑散体介质特征的竖向矩形均布荷载作用下地基附加应力改进计算方法。

4 各因素对附加应力的影响规律分析

由式（25）可知，地基附加应力与基础尺寸、点的位置（x轴、z轴坐标）、荷载q大小、土体内摩擦角φ、不均匀系数Cu等因素有关，为了深入研究地基附加应力的响应机制，下面将以竖向附加应力σz为例，探究各因素对附加应力的影响规律，包括参数分析和极差分析。

4.1 参数分析

本研究针对外加荷载大小、土体内摩擦角、不均匀系数等对荷载中心线上的竖向附加应力σz进行参数分析，探究各因素对竖向附加应力的影响规律。

各影响因素依据工程实际情况选取3 个不同的水平值，如表2 所示。

表2 各因素水平Table 2 Levels of various factors

在分析某个参数的影响规律时，其他参数均选取第Ⅱ水平值作为参数分析常量。此外，基础长边l为2 m，短边b为1 m，泊松比μ取0.2，所求点埋深z分别取0,0.5,1.0,2.0 m 共 4 个水平值。

下面依据表2 设置的参数，分析荷载中心线上各点竖向附加应力σz随深度的分布规律，所得参数分析结果如图4 所示。

由图4a 和4b 所示规律曲线可以得知，同一深度处的竖向附加应力随着内摩擦角和不均匀系数的增大而逐渐减小。这是由于附加应力在地基土中的扩散范围是随内摩擦角和不均匀系数的增加而增大的，根据静力平衡原理，附加应力扩散范围的增大，会导致附加应力值减小，这也证明了本文所得出附加应力解析解的合理性。

由图4c 可以得知，同一深度处的竖向附加应力随外加荷载的增大而逐渐增大，而其增量随外加荷载的增大而逐渐减小，这是由于附加应力在地基土中的扩散范围是随外加荷载的增加而逐渐增大的，根据静力平衡原理，附加应力扩散范围的增大会在一定程度上缓解附加应力的增大。

由以上分析可知，竖向均布荷载作用下地基竖向附加应力随内摩擦角和不均匀系数的增大而逐渐减小，随外加荷载的增大而逐渐增大，其增量随外加荷载的增大而逐渐减小。

4.2 极差分析

为探究各因素对附加应力响应的影响程度，确定影响附加应力的各因素主次顺序，下面采用正交试验设计方法，对各因素水平下的竖向附加应力σz展开极差分析。

本正交试验包括荷载大小、土体内摩擦角和不均匀系数3 个分析指标，每个指标有3 个水平，因此，此正交试验设计方案如表3 所示。

表3 正交试验方案及其附加应力解Table 3 Orthogonal test scheme with its additional stress solution

依据设定的正交试验方案，计算得到各方案竖向矩形均布荷载作用下，中心线上深度z=1 m 处点的竖向附加应力值（见表3）。

下面依据表3 中各方案的竖向附加应力结果，对各因素进行极差分析。

依据式（26）确定各因素水平下竖向附加应力σz（见表3）的平均值：

各因素水平下，竖向附加应力σz平均值的极差L由下式确定：

由式（27）获得的各因素水平下竖向附加应力σz平均值的极差，如表4 所示。

表4 不同因素水平下σz 平均值的极差Table 4 Mean value range of σz under different factor levels MPa

由表4 可以得出如下结论：影响竖向矩形均布荷载作用下地基竖向附加应力的因素，按其主次顺序依次为q、Cu、φ。

5 结论

地基土体为大量土颗粒无序排列的散体介质，因此，竖向荷载作用下地基土中附加应力向下、向外扩散传递，且其应力响应范围为以荷载作用域为顶面的锥体，该锥体边界形状与外荷载、土体内摩擦角和颗粒不均匀系数大小密切相关。据此，本文建立了考虑散体介质特征的竖向矩形均布荷载作用下，地基附加应力的改进计算方法，并且对附加应力解析解进行了参数分析和极差分析：

1）本研究在均布荷载作用下地基附加应力通用解析方法的基础上，采用二维积分，推导出竖向矩形均布荷载作用下地基附加应力的显式解析解，建立了考虑散体特征的地基附加应力的改进计算方法，该方法考虑了荷载大小和土体物理力学性质等众多因素的影响；

2）将本研究得到的解析解和文献[20]的解析解以及Boussinesq 解计算得到的附加应力进行了对比分析，验证了本研究给出的解析解的合理性和可行性，可为基础工程设计提供有力依据；

3）通过对本研究中解析解的参数分析和极差分析结果可知，影响附加应力的因素按其影响程度由大至小依次为荷载大小、颗粒不均匀系数、内摩擦角，且附加应力随颗粒不均匀系数和内摩擦角的增大而减小，随外加荷载的增大而增大，其增量随荷载增大而逐渐减小；

4）本研究中考虑的散体介质特征，更适用于粗粒土地基，而对于细粒土地基，其适用性有待进一步证明；

5）对于多层地基，各层土体的物理力学性质及力学参数不同，暂时无法直接使用本解析解，后续将对此展开相应研究。