基于Bezier 曲线的四足机器人Trot 步态优化

薛晨慷，李 光，易 静，谭薪兴

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

近年来，移动式机器人受到了社会各界的关注，越来越多的科研工作者对其进行研究[1]。当前，移动式机器人主要分为履带式、轮式、足式、爬行或蠕动式等[2]。履带式、轮式机器人对地形有严格要求，一般要在较平坦、无障碍物的地面工作，而足式机器人运动更灵活，可在复杂崎岖路面上行走，如沙地等[3]，可被应用于资源探查、军事运输[4]等方面。

足式机器人包括单足、双足、四足和六足机器人等[5]。与单足、双足机器人相比，四足机器人的运动稳定性更好、负载能力更强、运动灵活性更佳[6]；与六足机器人相比，则四足机器人结构简单[7]、成本较低，且具备更好的机动性。基于此，本研究选取四足机器人为研究对象。

目前，对四足机器人的研究主要集中在结构设计、运动规划、算法控制3 个方面[8]。其中运动规划在四足机器人中起着至关重要的作用，可分为路径规划和轨迹规划两个部分。合理规划足端轨迹有助于减小机器人触地时的冲击，减少对机体的伤害；而且足端轨迹对机器人的稳定性有着非常大的影响。

关于足端轨迹规划的方法，田俊等[9]提出了一种基于五次多项式的静步态足端轨迹，五次多项式规划足端轨迹能够保证加速度连续过度，缺点在于加速度处于不断加速减速的过程中，容易出现加速度过大的问题。马慧姝等[10]人利用相机拾取生物犬步行时的足端数据点，再通过三次B 样条曲线拟合的方法形成足端轨迹，但规划的轨迹曲线不经过拟合数据的原始点。Liu C.H.等[11]利用直线轨迹来规划四足机器人的足端轨迹，而直线轨迹的缺点在于抬腿和落地的瞬间速度以及加速度不为0。也有学者利用复合摆线[12]、椭圆曲线[13]等规划四足机器人的足端轨迹；利用函数公式规划足端轨迹的优点在于方法简单，但是会限制机器人足端轨迹的形状。

综上所述，本研究旨在遵守质心稳定的原则，结合四足机器人足端轨迹约束条件，利用Bezier 曲线规划四足机器人的足端轨迹，并在仿真平台上验证此步态的可行性；然后，将所得到的结果与复合摆线规划足端轨迹法得到的结果进行比较，以此验证Bezier曲线轨迹优化的可行性与有效性，以期为机器人足端轨迹的研究提供理论参考。

2 四足机器人结构及运动学模型

2.1 四足机器人结构

四足机器人的结构是根据四足哺乳动物的身体结构，并基于仿生学原理设计而成的。四足机器人主要由机身和4 条腿组成，根据腿部结构的不同可划分为全膝式、全肘式、外膝肘式和内膝肘式机器人。本研究采用的四足机器人为全肘式结构，每条腿有侧摆关节、髋关节和膝关节3 个关节，共3 个自由度，其中侧摆关节可以实现机器人的侧向运动，而髋关节和膝关节组合可以实现机器人的前后向运动以及俯仰运动。

2.2 四足机器人运动学模型

以四足机器人右前腿为例，采用标准D-H 法建立坐标系，其运动学模型如图1 所示。

图1 中，坐标系O{XW,YW,ZW}为世界坐标系；坐标系B{X,Y,Z}为机身坐标系，原点在机器人躯干的质心处，X轴正方向为机器人前进的方向，Z轴正方向为竖直朝上，Y轴的正方向根据右手定则确定。坐标系{0},{1},{2},{3}分别为侧摆关节、髋关节、膝关节以及足端的坐标系；θ1,θ2,θ3分别为3 个关节的关节转角；L1,L2,L3分别为侧摆、大腿、小腿3 根连杆的长度。

2.2.1 正运动学

以四足机器人的右前腿为例，依据所建立的坐标系，推导出机器人的运动学方程，其D-H 参数如表1 所示。

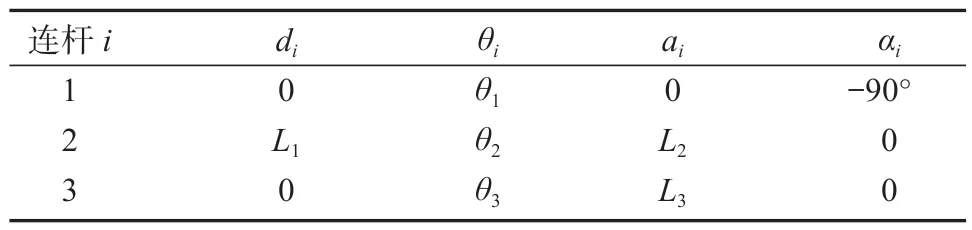
表1 右前腿D-H 参数表Table 1 D-H parameter table of right front legs

表1 中，ai为连杆长度，αi为关节扭角，di为关节距离，θi为关节转角。

机器人矩阵变换的通式为

于是得到如下各关节之间的变换矩阵：

以侧摆关节处坐标系为基座标，则足端对基座标的关系可以表示为

将表1 各参数带入式（5）中得到：

最终可以确定机器人足端正运动学方程为

2.2.2 逆运动学

如果机器人末端的位姿已经给出，要求其各关节的值，则需运动反解。逆运动学主要有代数法和几何法两种，本文采用代数法求逆运动学解。

1）求θ3。对式（7）进行平方和，得

令矩阵方程中对应元素相等，可得到：

利用式中第三个等式条件，同时令

经三角代换得

3）求θ2。利用式（13）中的两个等式条件，可以得到式（17）：

联立式（9）（10）（11）（17），计算可得

3 四足机器人足端轨迹规划与优化

根据抬腿顺序的不同，四足机器人步态可分为对称步态和不对称步态[14]。对称步态中，对角步态即Trot 步态，因其稳定性好、速度大[15]、重心偏移量小等优点成为最常见的研究步态。因此本研究采用Trot 步态进行研究，即行走过程中同时抬起、落下右前和左后腿（或左前和右后腿）。Trot 步态的时序图如图2 所示。

3.1 足端轨迹规划

根据参考文献[16]，可以得到复合摆线轨迹摆动相的方程为

式中：s为步长；h为抬腿高度；T为步态周期；λ为腾空率，即摆动相占整个步态周期的比例。

复合摆线规划的足端轨迹，其水平和竖直方向上速度、加速度分量在初始及结束的瞬间都为0。因此利用五次Bezier 曲线对复合摆线足端轨迹进行拟合。

Bezier 曲线于1962 年，由法国工程师Pierre Bezier 发明，并被成功应用于汽车车体工业设计，且将其广泛应用[17]。现如今Bezier 曲线主要用于Photoshop 等计算机绘图软件中曲线的绘制。Bezier曲线由线段与节点组成，可以依据起始点、控制点、终止点的坐标绘制出一条光滑的曲线[18]。如图3 所示为根据4 个点绘制的Bezier 曲线。图中控制点之间的连线为Bezier 曲线的控制多边形，生成的光滑曲线则为Bezier 曲线。

通过Bezier 曲线拟合得到的摆动相轨迹方程为

式中：i=0,1,…,5；Pxi为第i点的横坐标，取值为0,0,0.5s,0.5s,s,s；Pzi为第i点的纵坐标，取值为0,0.65h,1.3h,1.3h,0.65h,0。

设置步长s=20 mm，抬腿高度h=10 mm。

综上可得，复合摆线规划的足端轨迹和五次Bezier 曲线的足端轨迹拟合曲线如图4 所示。

结合参考文献[19]的研究可知，当足端轨迹与地面的底角为钝角时，冲击力更小，机器人行进更加稳定。因此在五次Bezier 曲线的基础上对轨迹进行修改，使其满足抬腿与落地时足端轨迹与地面的底角大于90°。为实现这一条件，需要在Bezier 曲线的起始点和终止点处额外添加3 个控制点，用该方法形成的Bezier 曲线最终共需12 个点控制。

首先对Z轴坐标进行重新规划，原五次Bezier曲线中最高点的纵坐标为1.3h，现将0～1.3h重新划分为6 等分。预设足端轨迹与地面的夹角为135°，并根据Px0=0,Pz0=0，Pz1=0.26h，通过斜率公式计算得到Px1=-0.13s，令Px2=Px1=-0.13s。用同样的方法可得到Px9=Px10=1.13s，最终得到的所有控制点的坐标如表2 所示。

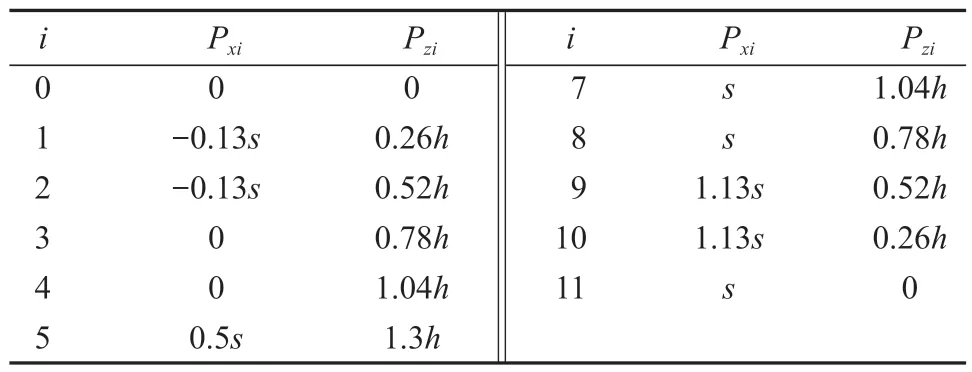
表2 初始控制点坐标Table 2 Initial control point coordinates

依据表2 中数据，最终得到一个周期内摆动相的足端轨迹方程，为

足端轨迹曲线如图5 所示。

对轨迹进行求导，可以得到其速度与加速度。由于Bezier 曲线控制点的坐标是常数，并且与变量t无关，因此对函数的求导转化为对伯恩斯坦多项式Bn,i(t)的求导：

最终计算得到轨迹的速度、加速度方程分别为

水平和竖直方向上的速度、加速度分量曲线图像分别为图6、图7 所示。

观察图5、图6、图7 中的曲线，发现形成的轨迹存在以下问题：

1）实际抬腿高度会超出预设的抬腿高度10%；

2）水平方向的速度和加速度在t=0 时刻过大；

3）水平方向上的速度和加速度在一个摆动相的时间内振幅过大。

针对以上问题，依据Trot 步态约束条件对控制点的坐标进行优化。

3.2 足端轨迹优化

Trot 步态约束条件如下：

水平方向为

竖直方向为

针对速度：通过改变3 个控制点的横坐标使两个一阶插值点为0，让速度等于0；

针对加速度：通过改变4 个控制点的横坐标使其两个二阶插值点为0，让加速度等于0；

针对抬腿高度：通过减小各控制点的纵坐标，使抬腿高度满足要求。

依据上述条件，经过多组数据对比，最终得到一组最优控制的点坐标，如表3 所示。

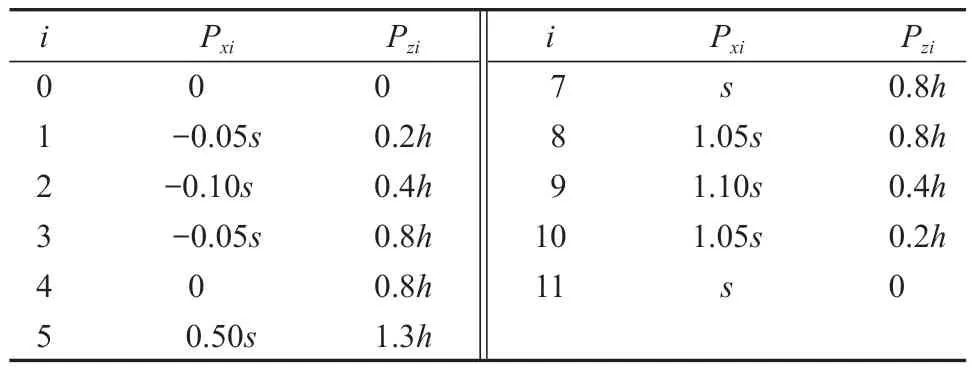
表3 最优控制点坐标Table 3 Optimal control point coordinates

优化后一个周期内摆动相轨迹函数为

一个周期内摆动相的足端轨迹如图8 所示。

其速度与加速度图像如图9 和图10 所示。

4 实验仿真与结果分析

4.1 仿真平台搭建

本文采用Solidworks 软件，以“YOBOGO”四足机器人为模型，建立四足机器人的虚拟样机。四足机器人的结构参数如表4 所示。

表4 四足机器人结构参数表Table 4 Structural parameters of quadruped robots

将模型导入Matlab/Simulink 中，结合实际情况，设置机器人的材料为铝合金，地面的接触刚度为1×104N/m，接触阻尼为1×102N/m，静摩擦系数为0.9，动摩擦系数为0.75。之后通过Simulink 模块并结合编写的程序，搭建如图11 所示仿真平台，并进行仿真实验。

4.2 仿真实验结果分析

4.2.1 实验一结果分析

实验一将复合摆线规划的足端轨迹与Bezier 曲线规划的足端轨迹进行对比。仿真过程中，除足端轨迹函数外，保证机器人的初始位置、步态周期T、占空比、步长s及抬腿高度h都完全相同。仿真结果如图12、13 所示，分别从机体前进距离、偏航距离、质心波动范围、足端的冲击力等方面判断机器人稳定性。又因机器人初始时刻距离地面有微小高度，落地期间产生的数据不准确，因此，为保证数据的有效性，对前两个周期即1 s 内的数据不予采用。

由图12 可看出，10 s 仿真时间内，无论是x轴方向的前进距离，y轴方向的偏航距离，以及z轴方向的波动范围，都有较大改善。由图13 所示不同步态下冲击力对比曲线可看出，Bezier 曲线规划的轨迹下，足端与地面接触时的冲击力更小。

4.2.2 实验二结果分析

实验二通过改变四足机器人步长s和抬腿高度h，对照步长s=20 mm，抬腿高度h=10 mm 时的冲击力和质心位移，找到足端轨迹最优步长和抬腿高度。设置步长范围为20～40 mm，间距为5 mm；抬腿高度区间为7～15 mm，间距为2 mm。每两组进行一次对比实验，选择数据更好的一组进入下一组对比实验，仿真时间设置为20 s。仿真结果见图14、15。

由图14 和15 可看出，h=9 mm，s=25 mm 时，机器人行走距离更远、速度更快，偏航距离及偏航角度更小；质心的上下波动范围以及足端冲击力几乎没变化。因此，此组步长及抬腿高度最佳。

5 结语

本研究应用Bezier 曲线规划四足机器人的足端轨迹。首先，采用五次Bezier 曲线对复合摆线规划的足端轨迹进行拟合，并依据足端轨迹规划约束条件，使足端冲击力最小的规划方法，对曲线的控制点进行增加和修改，最终得到Bezier 曲线规划四足机器人的足端轨迹方程。其次，在Matlab/Simulink 软件中建立机器人仿真平台，计算并建立机器人的正逆运动学模型；从机器人的前进距离、偏航距离、质心波动程度及落地时足端对地面的冲击力4 个方面，与复合摆线规划的足端轨迹进行对比，验证了Bezier曲线规划下的足端轨迹效率更高，机器人运动也更稳定。最后，在Bezier 曲线规划的足端轨迹下对抬腿高度及步长之间的关系进行研究，找到了抬腿高度与步长组合的最优解，完成对四足机器人行走的最优规划。结果表明：采用Bezier 曲线规划足端轨迹，能较好地优化机器人的运动效率及稳定性。