软黏土中静压桩打桩过程对土体强度和刚度影响的理论分析

周 航， 王增亮， 申 航， 李籼橙

(1.重庆大学山地城镇建设与新技术教育部重点实验室， 重庆 400045； 2.重庆大学土木工程学院， 重庆 400045)

静压桩问题是岩土工程中一个非常重要的问题. 静压桩打桩过程中会对周围土体产生扰动效应，桩周土体的应力状态、物理力学性质会发生改变，这对桩基的承载变形特性会产生重要的影响. 目前的研究主要关注打桩过程中桩周土体应力状态的改变、打桩后超静孔隙水压的消散以及挤土变形问题. 然而工程实际中，打桩后桩周土体的物理力学性质的改变也很重要，比如土体的强度和刚度变化，这对后续桩基承载变形的发挥有着重要的影响，土体强度的变化会直接造成桩基承载力的变化，而土体刚度的变化会影响桩基沉降变形的大小. 目前，关于土体强度和刚度变化的研究仍然较少，打桩后桩周土体强度和刚度如何变化，还没有完整和严格的理论分析方法.

对于打桩问题，在理论分析方面，主要是通过柱孔扩张理论、应变路径法和大变形有限元3种基本分析方法来开展. 其中，柱孔扩张理论作为一维的数学模型，由于其数学结构简单，很容易找到问题的精确解析解，所以广泛应用于解决岩土工程中的问题，例如沉桩挤土、桩基承载力、土体原位试验(静力触探试验、旁压试验、扁铲胀试验)、隧道开挖、锚板上拔、钻井稳定、压力注浆等问题. Gibson等[1]、Vesic[2]、Randolph等[3]最早将扩孔理论引入到岩土工程领域中用于解决土体原位试验、桩基础承载力以及沉桩挤土等问题，柱孔扩张理论主要是基于小变形理想弹塑性本构模型建立的. 随后，Carter等[4]、Yu等[5]给出了黏性摩擦材料以及考虑剪胀特性的土体的扩孔大变形闭合解析解. Stimpson等[6]采用相似变换技术给出了一种通用的孔扩张的计算方法. Cao等[7]推导了修正剑桥(modified Cam-clay，MCC)模型中的孔扩张问题的近似解析解. Chen等[8-10]给出了MCC模型土体中排水和不排水的柱孔扩张的弹塑性精确的解析解，该方法考虑了扩张平面外的应力对扩张力学响应的影响(三维效应). 周航等[11-16]考虑了非圆形以及各向异性初始应力的问题，建立了椭圆形柱孔扩张理论以及各向异性应力条件下的柱孔扩张理论. Mo等[17-18]基于非关联流动法则摩尔- 库伦模型推导了2层土中的孔扩张问题，给出了闭合解析解，并且利用该解析解来解释静力触探在多层土中的贯入问题.

根据现有研究成果，可以发现现有柱孔扩张理论框架包含2类：一种是Stimpson等[6]基于偏微分方程相似变换的技术提出来的，然而该方法存在一个缺陷，偏应力q采用最大主应力σ′1和最小主应力σ′3差来定义，即q=σ′1-σ′3，这不符合严格的弹塑性力学理论框架，因此，Stimpson等[6]的解答只能看作是近似解答. 另外一种就是Chen等[8-9]提出来的弹塑性精确解，该解答中偏应力q采用了严格的三维定义.

然而Chen等[8-10]的解答需要分别考虑土体的不排水和排水条件. 因此，现有柱孔扩张理论框架都存在缺陷. 本文结合Stimpson等[6]以及Chen等[8-10]2种方法的优势，并且去掉2种方法的缺点，提出一种通用的柱孔扩张求解方法，可以用于不排水解答，也可以用于排水解答.

本文针对软黏土中的打桩问题，采用柱孔扩张理论模型模拟打桩的过程，软黏土本构关系主要采用MCC模型来描述，结合弹塑性扩孔理论框架，建立扩孔基本控制偏微分方程，采用相似变换技术将偏微分方程组转化为常微分方程组，利用常微分方程数值求解技术获得柱孔扩张的MCC数值解答. 随后，基于该解答开展参数分析，探讨不同土体参数条件下打桩后桩周土体的强度和刚度的变化规律. 最终提出简化的设计公式，给工程设计提供参考.

1 柱孔扩张理论模型

图1给出了柱孔扩张(平面应变)理论模型，静压桩打桩的过程可以简化为无限大的土体中圆形孔洞扩张的过程(不考虑桩土之间的摩擦作用)，无限大土体在无穷远处受到均匀的水平应力场，水平应力为σh0(σh0=σr0=σθ0)，在垂直于扩孔平面的竖向应力为σv0(σv0=σz0)，土体的初始孔隙水压为u0. 扩孔过程中，柱孔扩张的压力为σa，对应的柱孔扩张半径为a. 孔洞周围的土体假设为弹塑性土体，土体本构关系采用MCC模型来描述. 随着孔洞压力的不断增大，孔周围的土体要发生屈服，孔洞附近的土体进入塑性状态，而离孔洞比较远的地方土体处于弹性状态，随着孔洞压力的不断增大，孔洞周围土体达到临界状态(p/q=常数)，这样在孔洞周围会形成3块区域：孔洞附近的临界状态区、塑性区以及远离孔洞的弹性区.

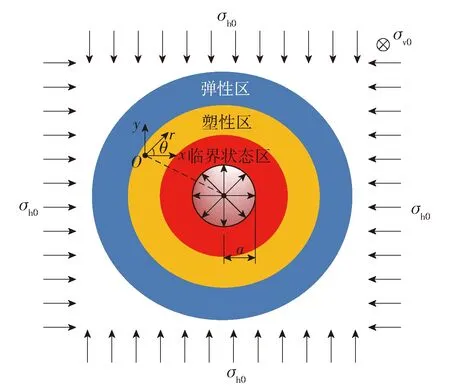
图1 柱孔扩张理论模型Fig.1 Model of cylindrical cavity expansion theory

此外，本文推导的解析解基于以下3个基本假设：1) 孔周的土体处于完全排水(超静孔隙水压始终为0)或者完全不排水(土体的体应变始终为0)状态，而本文主要研究软黏土中的打桩问题，因此，扩孔过程可以认为土体处于不排水状态，但是为了使得推导的解析解不失一般性，这里考虑2种排水条件；2) 孔扩张过程服从平面应变假设；3) 弹性区土体服从线弹性假设.

2 相似变换

柱孔扩张条件下，柱坐标对应的3个方向即为主应力方向，因此，平均应力p′和偏应力q可以分别写成

(1)

(2)

式中σ′r、σ′θ和σ′z分别为柱坐标下的径向、环向和竖向有效应力分量.

为了考虑大变形效应，采用物质导数来描述物理变量随坐标和时间的变化关系，即

(3)

式(3)可简写为

(4)

式中：v为土颗粒的径向运动速度；r为土体的径向坐标；t为扩孔的时间.

利用式(4)，大变形条件下的柱孔扩张几何方程可以表达为

(5)

相似变换技术的核心就是采用一个相似变量，使得偏微分方程转化为常微分方程，从而使得求解大为简化，柱孔扩张的相似变量可以写为

(6)

式中vp为弹塑性边界处土颗粒的径向速度.

采用相似变换后，有以下的关系：

(7)

(8)

(9)

3 本构关系

根据文献[19]，MCC模型的屈服面方程可以写为

F(p′,q,p′c)=q2-M2[p′(p′c-p′)]

(10)

式中：p′c为土体硬化参数，表示土体等向压缩下的屈服压力；M为临界状态线的斜率.

屈服面需要满足一致性条件dF=0，因此，MCC模型的屈服面一致性条件可以表达为

dF=mrdσ′r+mθdσ′θ+mzdσ′z-M2p′dp′c

(11)

式中

(12)

(13)

(14)

根据文献[8-9]，柱坐标下的MCC模型弹塑性的本构关系为

(15)

(16)

(17)

(18)

(19)

式中：E=2G(1+ν′)为土体的弹性模量，G=[3(1-2ν′)υp′]/[2(1+ν′)κ]为土体的剪切模量，ν′为土体的有效泊松比；υ为土体的体积比；κ为υ-lnp′平面加载- 再加载曲线的斜率.

4 弹塑性扩孔控制方程

对于弹塑性扩孔，孔洞周围将会出现3个区域：临界状态区域、塑性区域以及弹性区域.在临界状态区域和塑形区域中，应力必须满足平衡方程和本构模型屈服准则，而在弹性区中应力需要满足平衡方程.孔扩张的运动学方程则由土体的不排水条件(本文主要考虑不排水问题)、应变- 位移关系以及边界条件来控制.在弹塑性分界面(弹性区和塑形区的分界面)上面应力和位移必须保持连续.

4.1 临界状态区和塑性区

1) 应力平衡方程

对于柱孔扩张问题，应力需要满足平衡方程

(20)

式中u为土体的孔隙水压.

2) 本构方程

柱坐标条件下，本构关系可以写成式(15)中的统一矩阵形式.

3) 一致性条件

此外，屈服面需要满足式(11)中的一致性条件.

4) 连续性条件

在孔扩张过程中，土体需要满足质量守恒条件

(21)

5) 排水条件

完全不排水条件下，也即在扩孔过程中土体体积不变，有

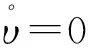
(22)

对于完全排水情况，孔隙水压的变化始终为0，即

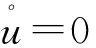
(23)

本文主要研究软黏土中的打桩问题，因此，仅考虑不排水条件.

上面5个条件即构成了弹塑性孔扩张的偏微分方程组，为了求解该方程组，需要采用相似变换技术，首先将物理变量作归一化，即

(24)

式中p′0为土体的初始平均应力.

然后将式(7)～(10)中的相似变换代入前面5个条件构成的方程组中，可以得到常微分方程组

(25)

式中

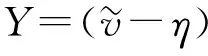
(26)

Dr=mr，Dθ=mθ，Dz=mz，Dξ=-M2p′

(27)

6) 边界条件

为了求解方程(25)，需要给出初始条件和边界条件，这里可以利用孔洞和弹塑性边界处的信息来确定.在弹塑性边界处，相似变量η=1.

(28)

(29)

(30)

(31)

(32)

(33)

式中：下标“0”表示初始状态；下标“p”表示弹塑性边界处;R为超固结比.进一步地，在孔口处相似变量需要满足

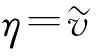
(34)

结合控制方程和上述边界条件编写MATLAB微分方程组数值求解程序，可以获得临界状态区和塑性区的半解析解.

4.2 弹性区

在弹性区，土体应力应变关系服从胡克定律，有

(35)

(36)

Δσ′z=ν′(Δσ′r+Δσ′θ)

(37)

式中ur为土体的径向位移.

在弹性区，土体需要满足式(20)中的应力平衡方程，但是需要注意的是弹性区超静孔隙水压等于0，土体的孔隙水压等于初始孔隙水压u0, 因此，式(20)可简化为

(38)

将方程(35)～(37)代入方程(38)，可以得到关于径向位移的偏微分方程

(39)

采用变换

(40)

式中rp为弹塑性边界的半径，方程(39)可以简化为常微分方程

(41)

方程(41)存在闭合解析解

(42)

式中C1和C2为常数，可以通过弹性区的边界条件求得.注意到当η→+∞时，径向位移必须消散为0，因此，C1必须为0，方程(42)可以简化为

(43)

因此，将方程(43)代入方程(35)～(37)获得

(44)

(45)

(46)

为求解C2常数，需要利用弹塑性边界处(η=1)应力连续的条件，因此，应力和位移的最终表达式可以写为

(47)

(48)

(49)

(50)

5 半解析解的验证

为了验证本文提出的柱孔扩张通用半解析解的正确性，利用本文解答分别计算完全不排水和完全排水2种情况，然后分别与Chen等[8-9]提出来的完全不排水和完全排水解答进行对比，计算参数与文献中保持一致.主要对比了排水(如图2所示)和不排水(如图3、4所示)的柱孔扩张压力扩张关系.利用MATLAB 2018中的“ODE45”函数可以求得方程(25)的数值解，对于不排水问题需要采用方程(22)的条件，对于排水问题需要采用方程(23)的条件.可以发现，本文计算得到的排水解答和不排水解答与文献中的完全一致.本文的解答是一个通用解答，通过式(25)来计算，而Chen等[8-9]提出来的方法需要分别考虑排水和不排水2种情况，并且2种情况的推导方式也不一样.

图2 排水柱孔扩张压力- 扩张关系本文解答与文献[8]中的解答对比Fig.2 Comparison of the proposed solution for drained cylindrical cavity expansion pressure-expansion relations with the solution in Ref. [8]

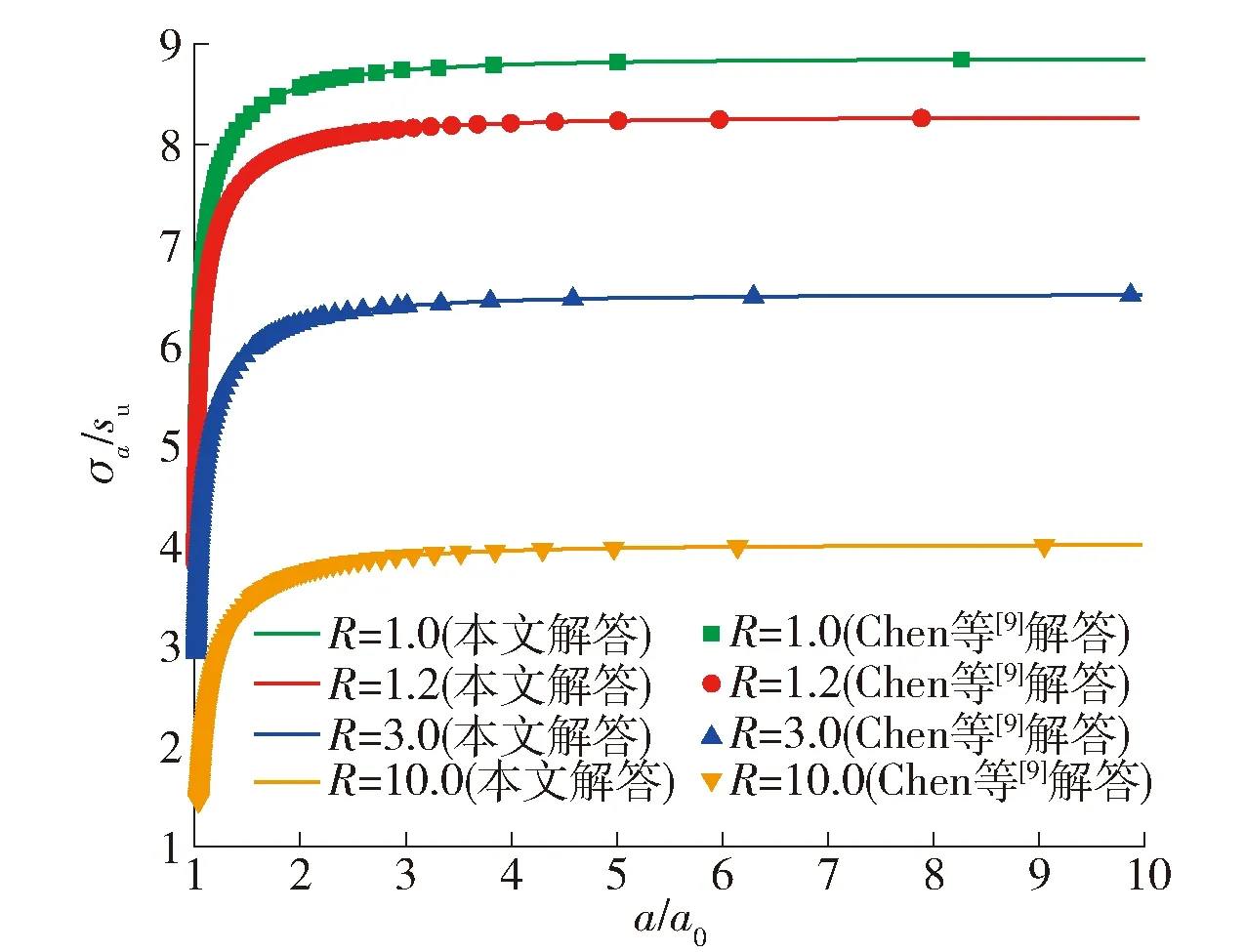
图3 不排水柱孔扩张压力- 扩张关系本文解答与文献[9]中的解答对比Fig.3 Comparison of the proposed solution for undrained cylindrical cavity expansion pressure-expansion relations with the solution in Ref. [9]

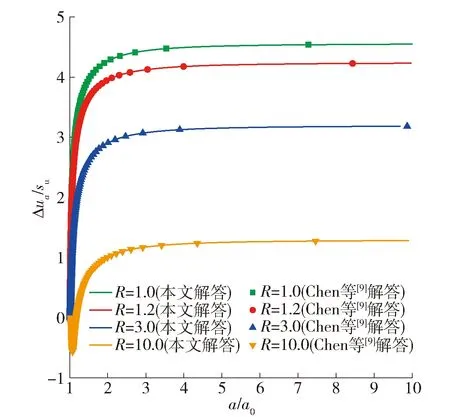
图4 不排水柱孔扩张超静孔隙水压- 扩张关系本文解答与文献[9]中的解答对比Fig.4 Comparison of the proposed solution for undrained cylindrical cavity expansion excess pore pressure-expansion relations with the solution in Ref. [9]

6 桩周土体强度和刚度的变化

从MCC模型的理论框架可知，土体的强度和刚度(剪切模量)[7]可以表示为

(51)

G=[3(1-2ν′)υp′]/[2(1+ν′)κ]

(52)

对于不排水孔扩张问题，土体的体积比υ保持不变，始终等于初始值υ0，而其余的本构参数κ、λ、M、ν′在扩孔过程中也是一个常量.可以发现，土体的强度和刚度都只跟平均有效应力p′有关，并且正比于平均有效应力p′.因此，得到

(53)

式中：δ为打桩后的土体强度(或剪切模量)和初始土体强度(或剪切模量)之比；su0为土体的初始强度；G0为土体的初始剪切模量.

可以发现，打桩后桩周土体强度和剪切模量的变化可以采用δ表示，因此，下面主要讨论不同土体参数以及不同土体本构模型条件下，该参数的变化规律.

7 参数分析

从上述推导可以发现，对于MCC模型中不排水柱孔扩张解答，主要取决于以下6个独立的归一化的变量:G/p′0、ν′、(λ-κ)/υ、M、R、Λ≜q0/p0，因此，参数分析主要围绕这6个变量开展.

图5～10分别给出了这6个参数对打桩后桩周土体强度和剪切模量变化规律的影响.图 5给出了不同G/p′0条件下δ沿着桩周土体径向变化规律.G/p′0取值范围为20～500(考虑了超软土和较硬土).结果表明，打桩后桩周土体的强度和剪切模量的变化规律可以分为3块区域：完全扰动区、塑性扰动区(过渡区)和未扰动区.在完全扰动区域，土体的应力水平达到临界状态；在塑性扰动区域，土体进入塑性，但是还未达到临界状态；在未扰动区域，土体处于弹性状态.随着G/p′0的不断增加，桩周土体的完全扰动区域以及塑性扰动区域不断扩大，土体强度的退化明显.完全扰动区域的大小为2a～10a(a为桩体半径).图 6给出了不同ν′下δ沿着桩周土体径向变化规律.可以发现，随着ν′的不断增加，完全扰动区域以及塑性扰动区域不断扩大，然而在完全扰动区域土体的δ变化不明显.图7给出了不同(λ-κ)/υ下δ沿着桩周土体径向变化规律.可以看出，(λ-κ)/υ的变化并不影响完全扰动区域以及塑性扰动区域的大小，其仅影响完全扰动区域内土体的δ的大小，并且随着(λ-κ)/υ的不断增大，完全扰动区域内土体的δ不断减小，土体强度和刚度退化明显.图8给出了不同M下δ沿着桩周土体径向变化规律，可以发现M对塑性扰动区域的大小以及完全扰动区域的大小影响不大，然而对完全扰动区域土体的δ有很大影响.当M不断增大时，完全扰动区域土体的δ不断减小.当M=0.5时，完全扰动区域的土体的强度和刚度表现出硬化的特征；当M>1.0时,完全扰动区域的土体强度和刚度表现出软化的特征.图9反映了不同R下δ沿着桩周土体径向变化规律，可以看出，当R=1时(正常固结土)，完全扰动区域土体的δ小于1，土体的强度和刚度表现出软化的特征；当R>1时(超固结土), 完全扰动区域土体的δ大于1，土体的强度和刚度表现出硬化的特征.图10给出了不同Λ下δ沿着桩周土体径向变化规律，可以发现：当Λ=1时，桩周土体的δ等于1，表明土体未受到扰动；而当Λ>1时，桩周土体的δ大于1，土体表现出硬化；当Λ<1时，桩周土体的δ小于1，土体表现出软化.由此可见，参数M(反映土体的强度)、R(反映土体的应力历史)、Λ(反映了土体的初始应力比q0/p0)这3个参数决定了打桩后桩周土体的强度或刚度是硬化还是软化.

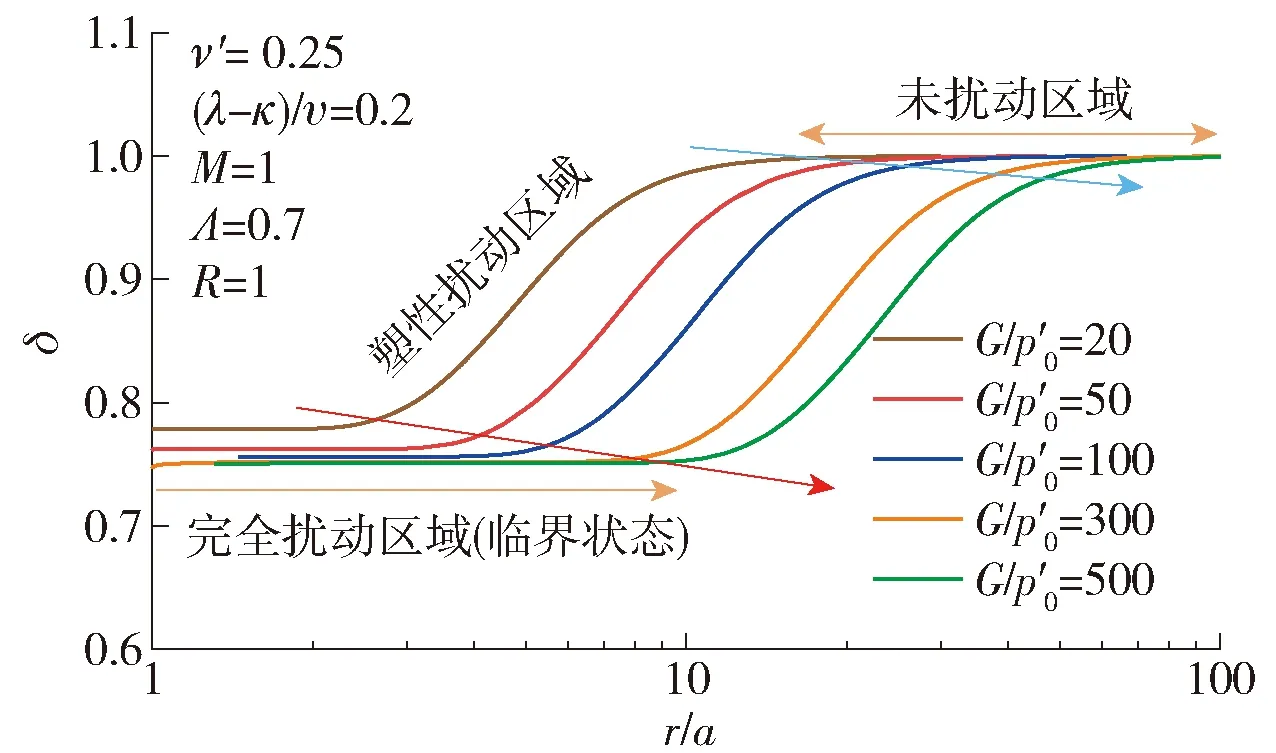
图5 不同G/p′0下δ沿着桩周土体径向变化规律Fig.5 Variation of δ along the radial distance around the pile for different G/p′0

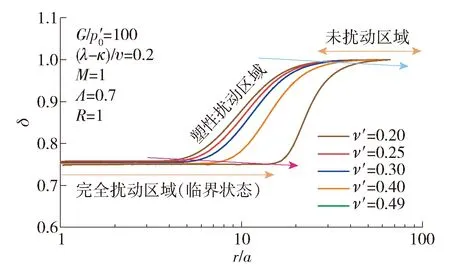
图6 不同ν′下δ沿着桩周土体径向变化规律Fig.6 Variation of δ along the radial distance around the pile for different ν′

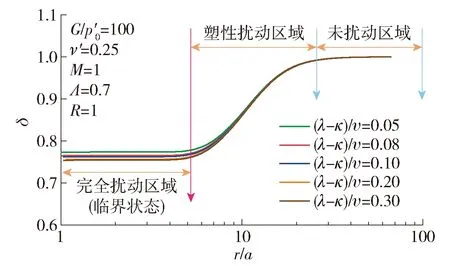
图7 不同(λ-κ)/υ下δ沿着桩周土体径向变化规律Fig.7 Variation of δ along the radial distance around the pile for different (λ-κ)/υ

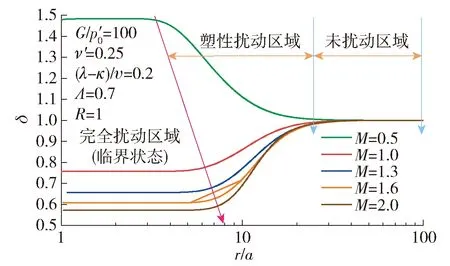
图8 不同M下δ沿着桩周土体径向变化规律Fig.8 Variation of δ along the radial distance around the pile for different M

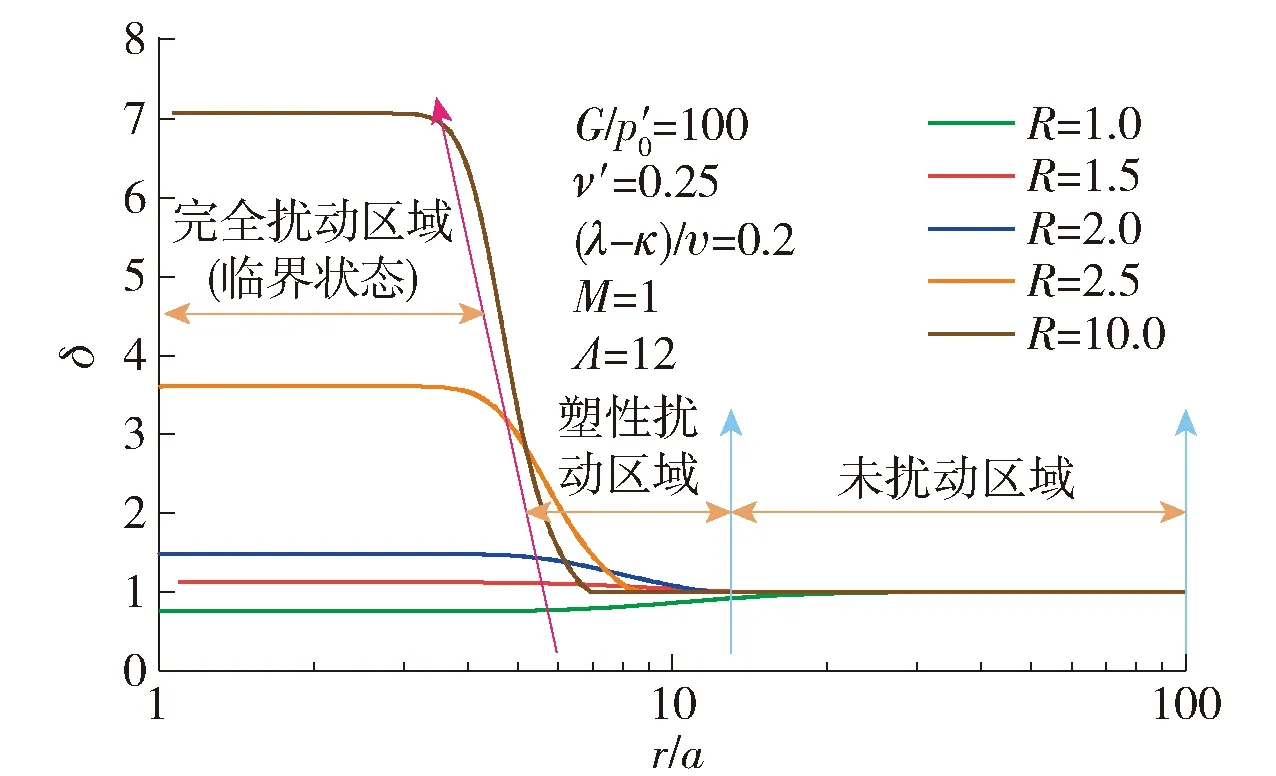
图9 不同R下δ沿着桩周土体径向变化规律Fig.9 Variation of δ along the radial distance around the pile for different R

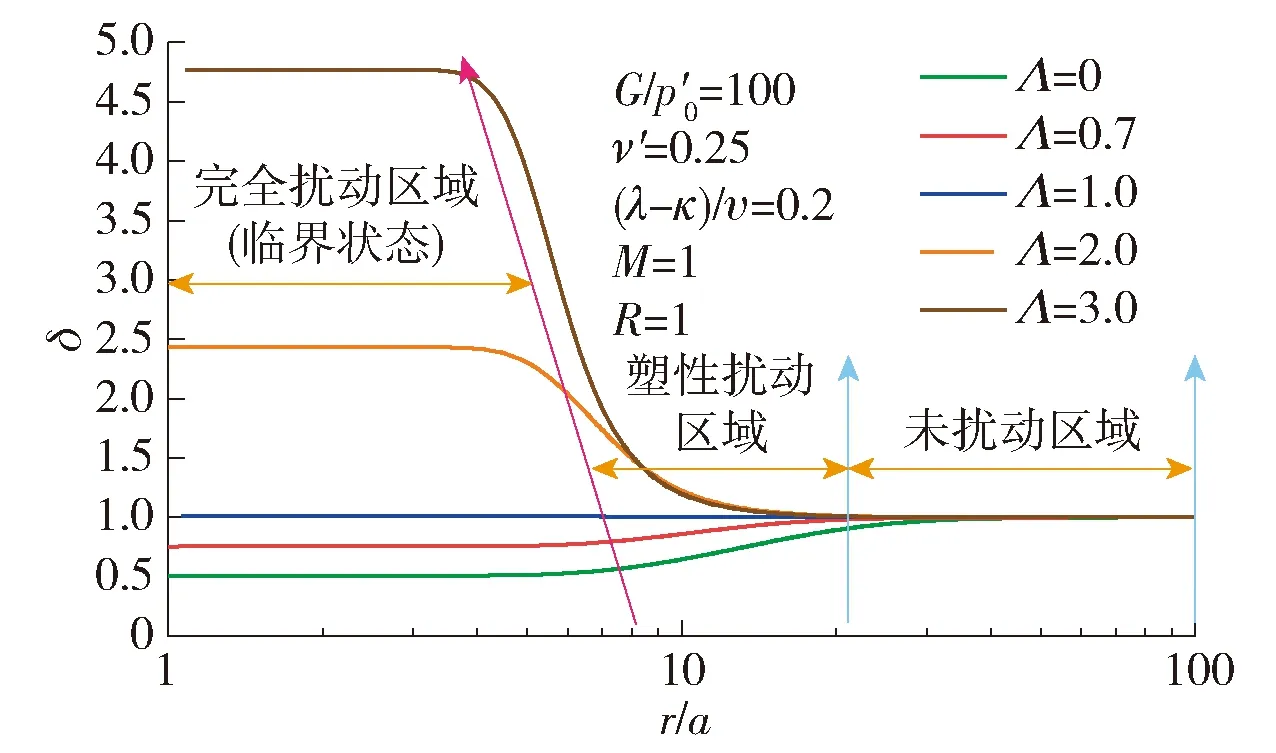
图10 不同Λ下δ沿着桩周土体径向变化规律Fig.10 Variation of δ along the radial distance around the pile for different Λ

完全扰动区域离桩身最近，该区域的属性直接决定了静压桩的承载变形特性.因此，如图11～16所示，进一步地探讨了完全扰动区域土体的δ和半径rc随着6个参数的变化规律.图11表明，完全扰动区域土体的δ随着G/p′0的增大呈现幂函数的减小；rc随着G/p′0的增大呈现幂函数的增大.图12表明，完全扰动区域土体的δ随着ν′的增大略微线性减小(变化不大)，而rc随着ν′的增大指数型增大.图13表明，随着(λ-κ)/υ的不断增大，完全扰动区域土体的δ和rc均按照指数形式递减.从图14可以看出，随着M的不断增大，土体的δ指数型减小而rc指数型增大.图15表明，土体的R增大会导致完全扰动区域土体的δ和rc分别按照线性增大和指数型递减.图16表明，土体的Λ不断增大，δ指数型增大而rc指数型递减.

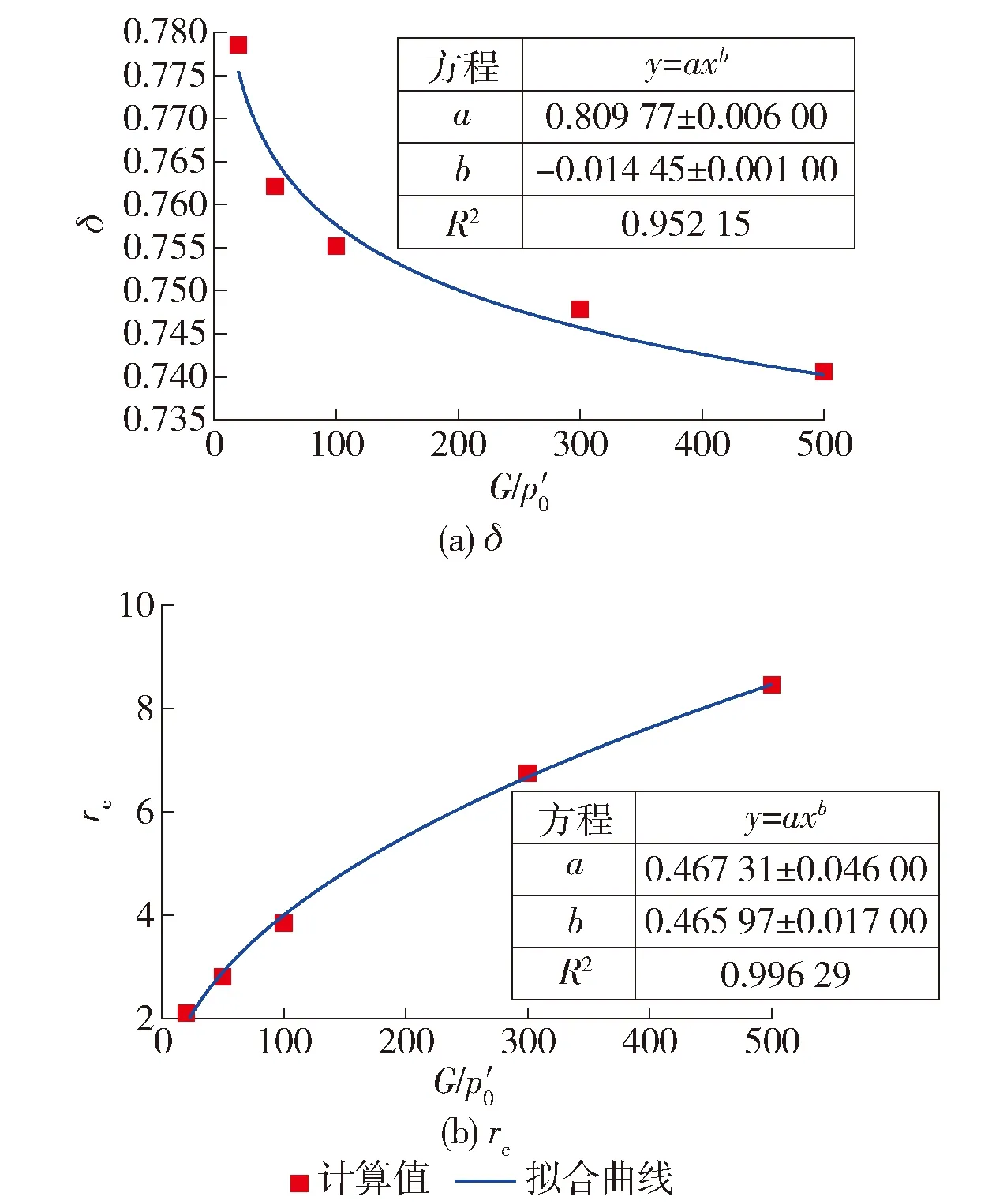
图11 δ和rc随G/p′0 的变化规律Fig.11 Variation of δ and rc with different G/p′0

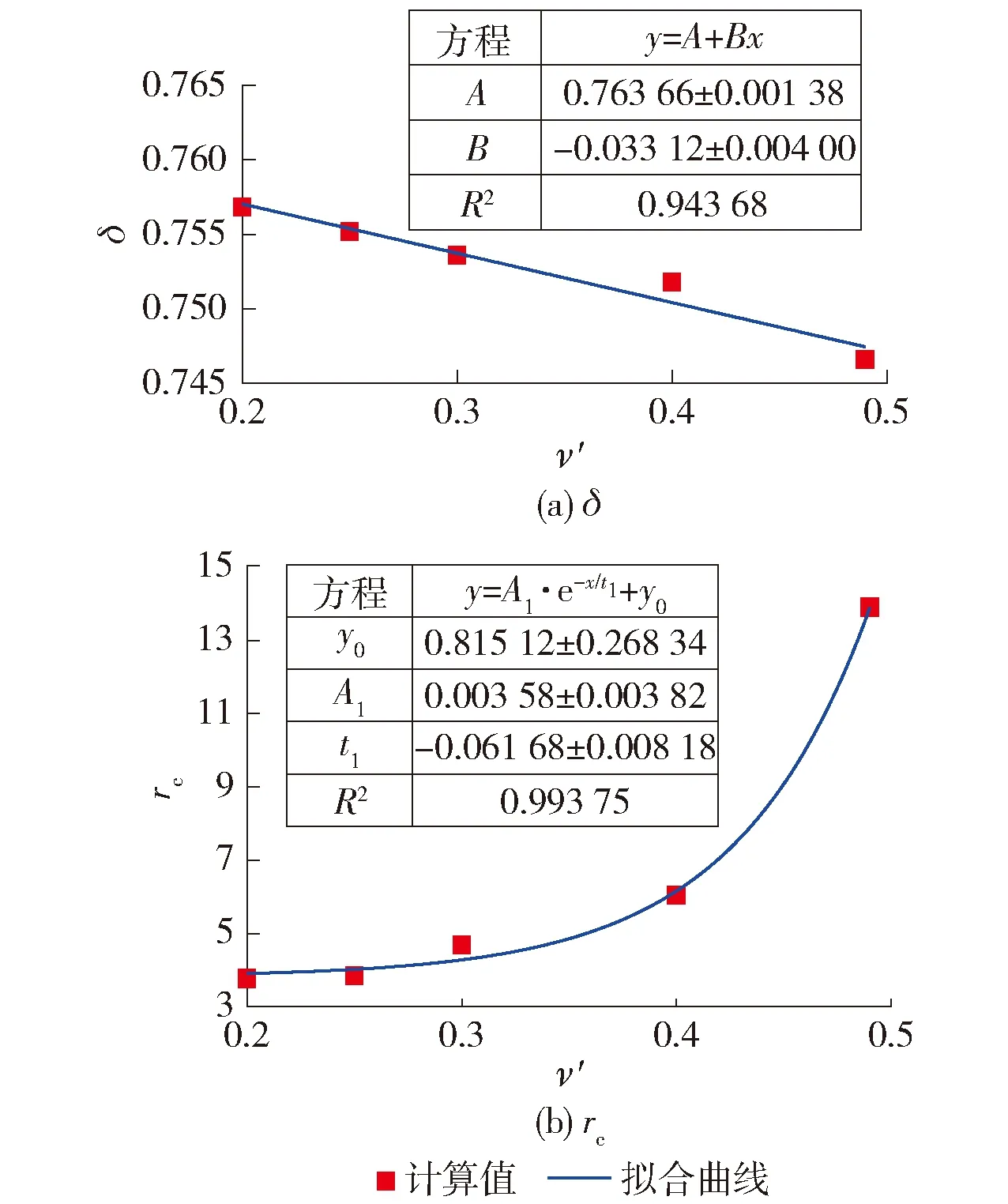
图12 δ和rc随着ν′的变化规律Fig.12 Variation of δ and rc with different ν′

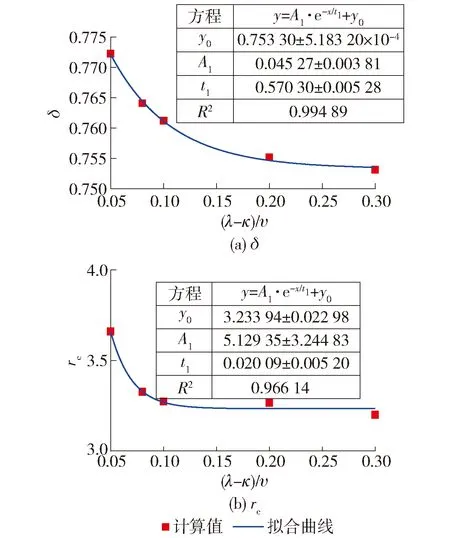
图13 δ和rc随(λ-κ)/υ的变化规律Fig.13 Variation of δ and rc with different (λ-κ)/υ

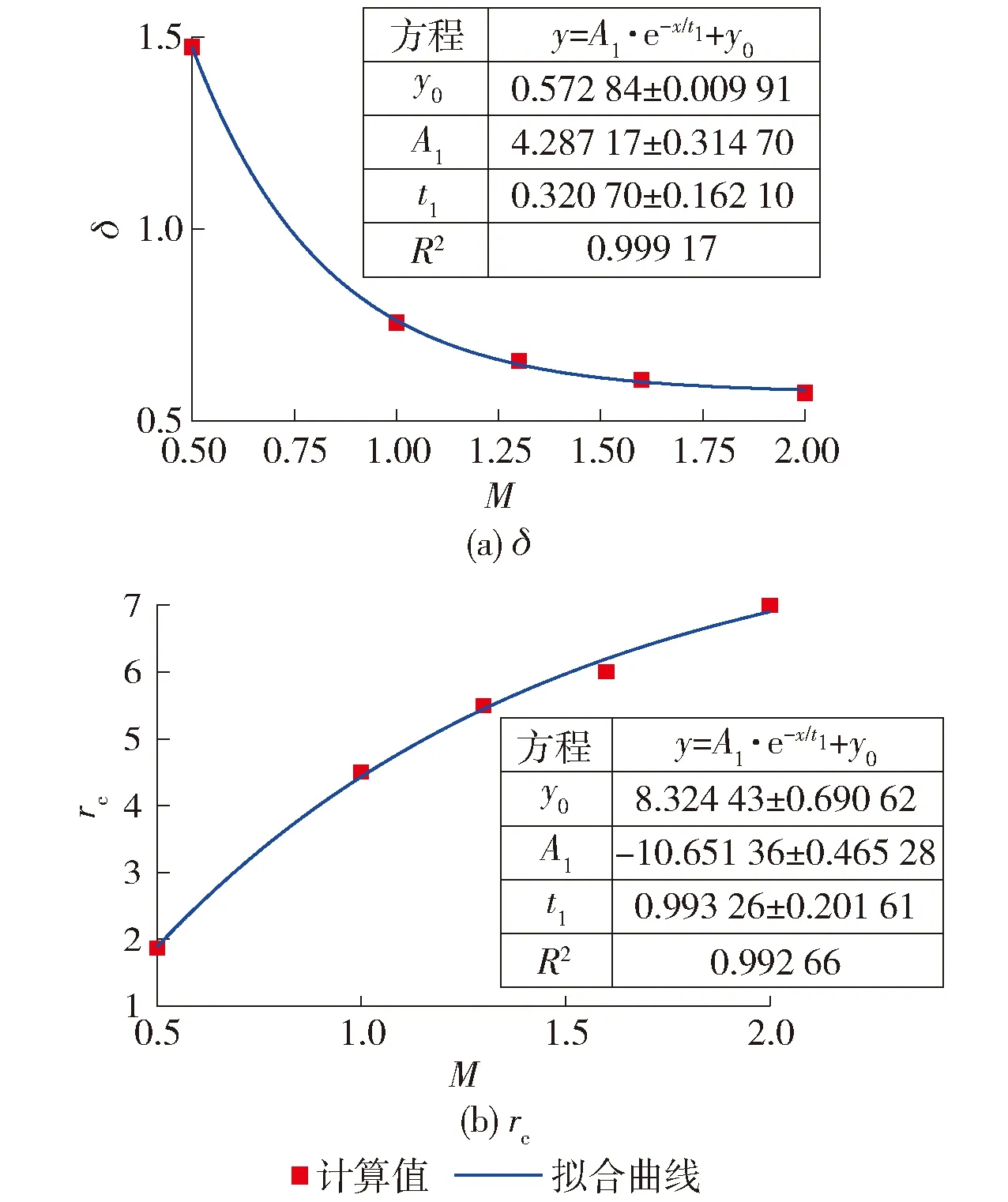
图14 δ和rc随M的变化规律Fig.14 Variation of δ and rc with different M

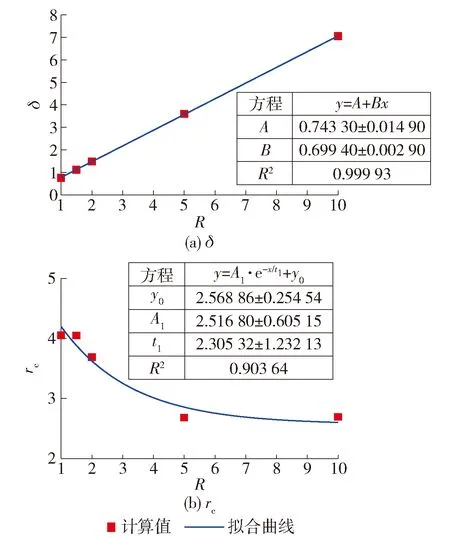
图15 δ和rc随R的变化规律Fig.15 Variation of δ and rc with different R

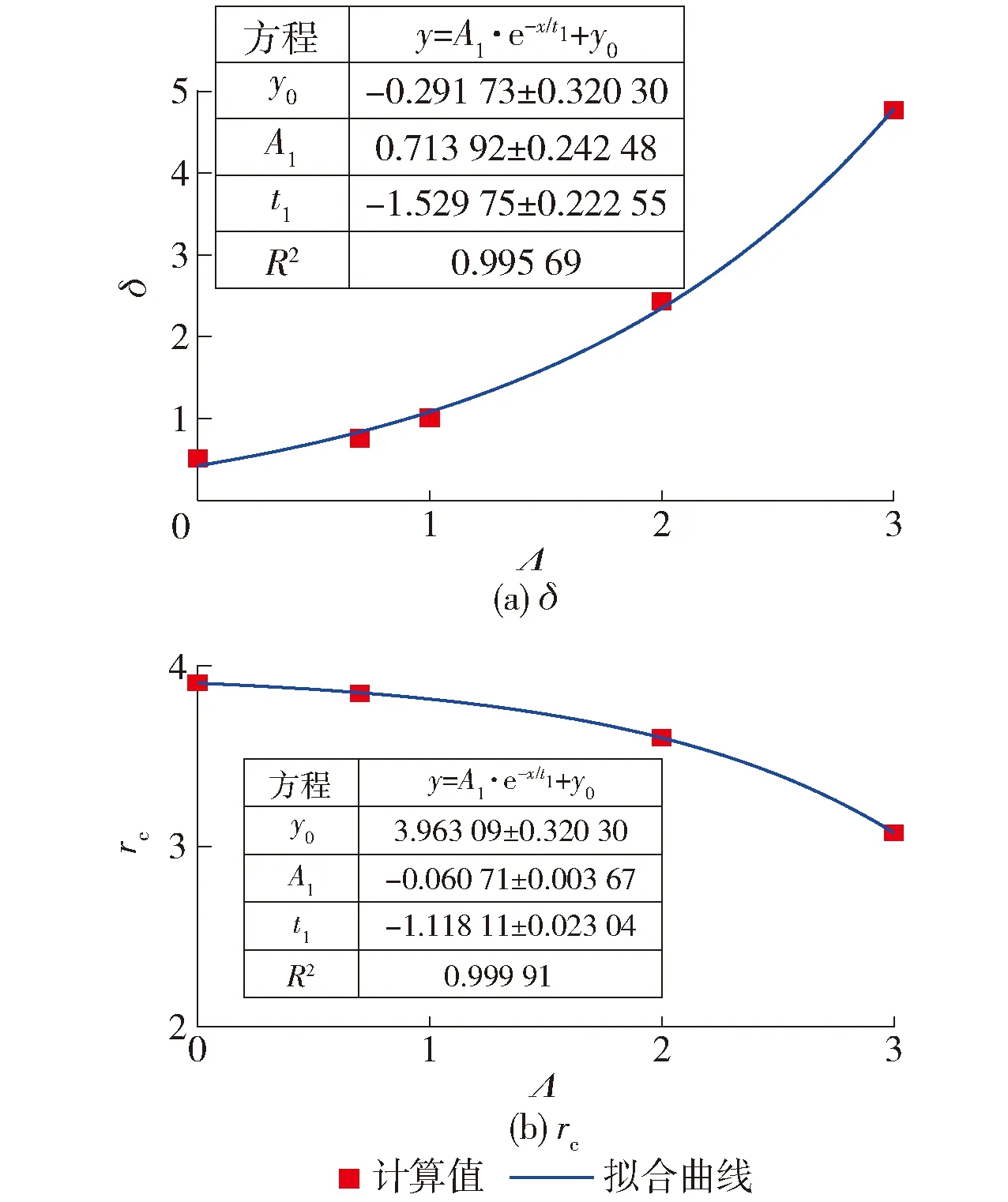
图16 δ和rc随Λ的变化规律Fig.16 Variation of δ and rc with different Λ

8 结论与建议

1) 本文推导的柱孔扩张统一的半解析解采用相似变换技术，可以适用于任意的塑性本构模型，并且能够考虑完全不排水、完全排水条件.

2) 采用不排水柱孔扩张模拟静压桩打桩过程，利用柱孔扩张后土体应力状态的变化来评估桩周土体的强度和刚度的变化，可以发现，打桩后桩周土体的强度和剪切模量的变化规律可以分为3块区域：完全扰动区、塑性扰动区、未扰动区.在完全扰动区域，土体的应力水平达到临界状态；在塑性扰动区域，土体进入塑性但是还未达到临界状态；在未扰动区域，土体处于弹性状态.

3) 利用土体的δ来评估打桩后桩周土体强度和刚度的变化，讨论了不同参数对土体的δ的影响，可以发现，参数M、R、Λ决定了打桩后桩周土体的强度或刚度是硬化还是软化.

4) 参数分析结果表明：随着G/p′0的不断增加，桩周土体的完全扰动区域以及塑性扰动区域不断扩大；随着(λ-κ)/υ的不断增大，完全扰动区域内土体的δ不断减小，土体强度和刚度退化越明显；M不断增大时，完全扰动区域土体的δ不断减小；对于正常固结土或者Λ<1，土体呈现软化特征；对于超固结土或Λ>1，土体呈现硬化特征.

5) 本文建立的静压桩打桩后桩周土体强度和刚度变化的分析方法，为工程设计中更加准确地计算考虑沉桩挤土效应的静压桩承载力提供了一个简单而又严谨的理论方法，改善了现有分析方法中对打桩后桩周土体强度和刚度特性的变化考虑不足的缺点.此外，需要指出，本文主要讨论打桩后桩周土体强度和刚度的变化，而并未讨论打桩后随着时间的迁移，由于超静孔隙水压的变化而产生的强度和刚度变化的时效性.