超磁致伸缩换能器设计及其涡流损耗分析

刘 强，李 婧，张雄伟，贺西平*

(1 陕西师范大学 物理学与信息技术学院，陕西 西安 710119;2 中北大学 先进制造技术山西省重点实验室，山西 太原 030051)

超声换能器是完成电能和机械能转化的装置，在工业中使用最广泛的换能器是磁致伸缩换能器和压电换能器[1]。超磁致伸缩材料(giant magnetostrictive material, GMM)与压电陶瓷材料相比，其导热系数高，散热性好，响应速度快，负载力强，且具有磁致伸缩系数大，能量密度高，无过热失效。GMM广泛应用于换能器、传感器、振动能量收集等领域[2-6]。

当换能器的横向尺寸小于1/4波长时，可忽略横向振动对纵振频率的影响，故传统超磁致伸缩换能器一般根据一维纵向理论进行设计。为满足换能器高功率和高机械强度的要求，就必须加大其横向尺寸，由于泊松效应，纵向振动与径向振动之间产生较强的相互作用，形成耦合振动，此时超磁致伸缩换能器的横向振动不可忽略，一维理论设计结果将会产生较大的误差。为此，Mori等[7]提出了解决各向同性实心圆柱耦合振动的表观弹性方法；任树初[8-9]对大尺寸横向振动体的谐振频率进行了计算研究；Karafi等[10]基于表观弹性法，设计了一个横向尺寸大于1/4波长的夹心式超声换能器的设计程序。

在高频磁场中工作时，材料中会产生严重的涡流损耗，涡流的存在会削弱驱动线圈所提供的磁场，并改变磁场的均匀性。与频率相关的磁滞、涡流不仅会降低超磁致伸缩材料的能量转换效率，还会改变换能器的温度分布，而温升会引起换能器谐振频率降低，振幅稳定性下降[11]。Meng等[12]研究了TbDyFe/环氧复合材料的磁能损耗及其频率依赖性，发现主要损耗来自复合材料的磁滞损耗和整体TbDyFe合金的涡流损耗。黄文美等[13]测量了TbDyFe合金在不同频率和磁通密度的动态磁特性曲线，提出了一种变温条件下磁致伸缩材料的高频损耗计算模型。Xu等[14]通过建立GMM的动态损耗模型预测交变磁场和预应力下GMM的动态磁致伸缩效应。随着激励频率的增加，涡流损耗逐渐主导能量损失，而异常损失的影响并不明显。以上研究表明：分析和控制涡流损耗对于提高超磁致伸缩换能器的工作效率至关重要。

为降低稀土棒的涡流损耗，减小传统解析法设计超磁致伸缩换能器存在的误差。本文基于耦合振动理论设计了超磁致伸缩换能器，由表观弹性法求出换能器的等效弹性常数，对换能器的共振频率进行了计算。利用有限元软件对设计的换能器进行模态分析，并对GMM棒的涡流损耗问题进行计算。进一步研制了一种超磁致伸缩换能器的样机，对换能器进行实验测试，比较分析了换能器共振频率的理论计算值、仿真计算值和实验测量值的误差。

1 耦合振动理论及换能器设计

超磁致伸缩换能器的结构图如图1所示。在导磁圆筒与后盖板上设置螺纹，导磁圆筒通过螺纹固定在后盖板上。前盖板、后盖板、导磁块、永磁体、GMM棒通过预紧螺栓和螺母固定。

1.前盖板 2.螺母 3.导磁块 4.永磁体 5.导磁圆筒 6.线圈 7.GMM棒 8.后盖板 9.螺栓

1.1 耦合振动理论

半径为r、长为2l的圆柱形弹性振动体，在不考虑剪切形变，只考虑伸缩形变的条件下，其振动等效为细圆柱的纯纵向振动和薄圆盘的纯径向振动。在不同方向的振动可以用不同的表观弹性常数进行表征。根据弹性力学理论，在柱坐标下，振动体内任一点的正应力σr、σθ、σz与正应变εr、εθ、εz之间的关系为

(1)

(2)

(3)

式中，E和v分别为材料的弹性常数及泊松比。在准静态情况下，σr=σθ，由式(1)～(3)可得

Ez=E/(1+2v/n)，

(4)

Er=E/[1-v2+nv(1+v)]。

(5)

式中：n= ―σz/σr，表示振动体内纵向振动与径向振动之间的耦合系数，n决定了2个一维振动之间的耦合程度以及相互关系；Ez=σz/εz、Er=σr/εr分别为振动体在z及r方向的表观弹性常数。两端自由的圆柱体纵向频率方程和径向频率方程分别为

sin(2kzl)=0，

(6)

krrJ0(krr)-(1-v)J1(krr)=0。

(7)

式中：kz=ω/Cz，kr=ω/Cr，Cz= (Ez/ρ)1/2，Cr= (Er/ρ)1/2，kz、kr及Cz、Cr分别表示等效的纵向及径向振动的波数以及声速，ω为角频率，ρ为密度;J0及J1分别为零阶以及一阶贝塞尔函数。由(6)～(7)式可得

2kzl=iπ，

(8)

krr=R(j)。

(9)

式中：i，j=1,2,3…。

根据上述各式可得出圆柱体耦合振动的耦合系数

(10)

根据(10)式求得耦合系数n，带入式(4)～(5)，可得到换能器各部分的等效弹性常数和波数。

1.2 换能器设计

将换能器的前后盖板、GMM看作杆，假设其进行简谐振动，杆纵向振动的波动方程为

(11)

式中：ξ(x)为质点的位移函数；S(x)为杆的横截面积；k为波数。圆锥形截面杆的振速V(x)、弹性力F(x)的通解为

(12)

(13)

式中：A、B为待定系数；Z=ρcS为超声振子的特征声阻抗；α=(D1-D2)/D1l，D1、D2、l分别为圆锥形变截面杆大端直径、小端直径以及圆锥形截面杆的长度；S(x)为任意位置处圆锥形截面杆的横截面积。

节面位于换能器的后导磁块与后盖板的结合面，后盖板的长度即为1/4波长。换能器的前端和后端处于自由状态，所以F1(0) =F5(l5) = 0。在节面处的振速为0，即V1(l1) =V2(0) = 0，根据换能器各界面处的振速及力连续边界条件，可得到频率方程为

(14)

式中，A5和B5为待定系数。

表1为换能器的材料参数，根据换能器的频率方程与已知参数，基于一维纵向振动理论，求得换能器的共振频率。并采用表观弹性法求出换能器各部分的等效弹性常数和波数，由频率方程以及参数求出修正后换能器的共振频率。

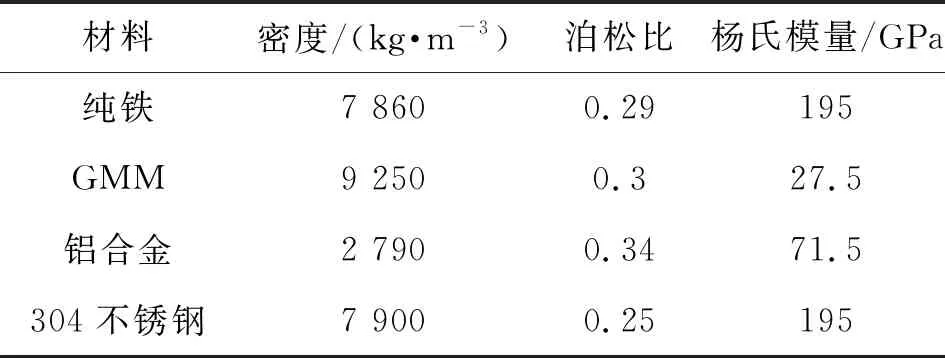
表1 材料参数

2 仿真分析和实验

为了验证超磁致伸缩换能器理论计算的结果，根据图1设定换能器的尺寸为：l1=62.5 mm，l2=6 mm，l3=20 mm，l4=6 mm，D1=62 mm，D2=D3=D4=20 mm，d5=50 mm(变幅杆小端直径)，D5=62 mm(变幅杆大端直径)，l5=7 mm。

在Solidworks中建立超磁致伸缩换能器的模型导入ANSYS有限元软件中，采用压磁-压电比拟法对换能器进行模态分析，图2为超磁致伸缩换能器的振动模态，换能器的共振频率为21 021 Hz，换能器后盖板的振幅最小,前盖板的振幅最大,说明了换能器结构的合理性。

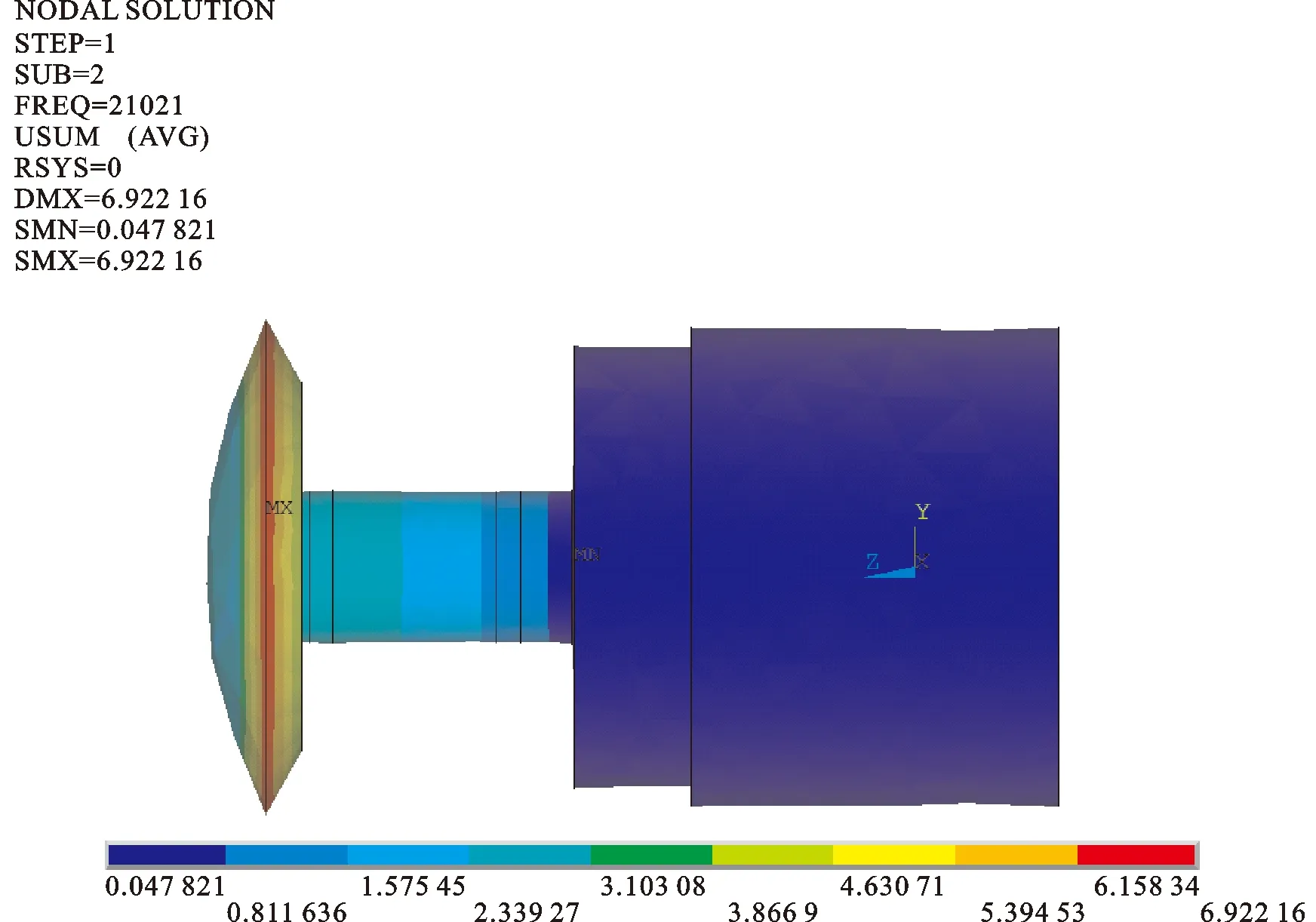
图2 换能器的振动模态

在有限元软件中对两种结构GMM棒的涡流损耗进行仿真计算，分别为未处理的GMM棒和切片处理的GMM棒，根据换能器的工作频率计算出切片处理GMM棒中切片厚度为1.3 mm左右[15]。设置线圈匝数为350匝，激励电压为45 V，图3为仿真计算得到两种GMM棒的涡流损耗分布图，未处理GMM棒(图3a)的涡流损耗主要集中在外径表面附近，内部较小；而切片处理GMM棒(图3b)外表面的涡流损耗明显减小。仿真计算得到未处理GMM棒的涡流损耗为0.484 W，切片处理GMM棒的涡流损耗为0.155 W，切片处理GMM棒的涡流损耗比未处理GMM棒减小了67.98%。

图3 不同结构GMM棒的涡流损耗分布图

研制的样机如图4所示，利用阻抗分析仪对换能器进行频率测试。

图4 换能器的样机

图5为频率测量得到的超磁致伸缩换能器的阻抗曲线，从图中可以看出换能器的共振频率为20.790 kHz。

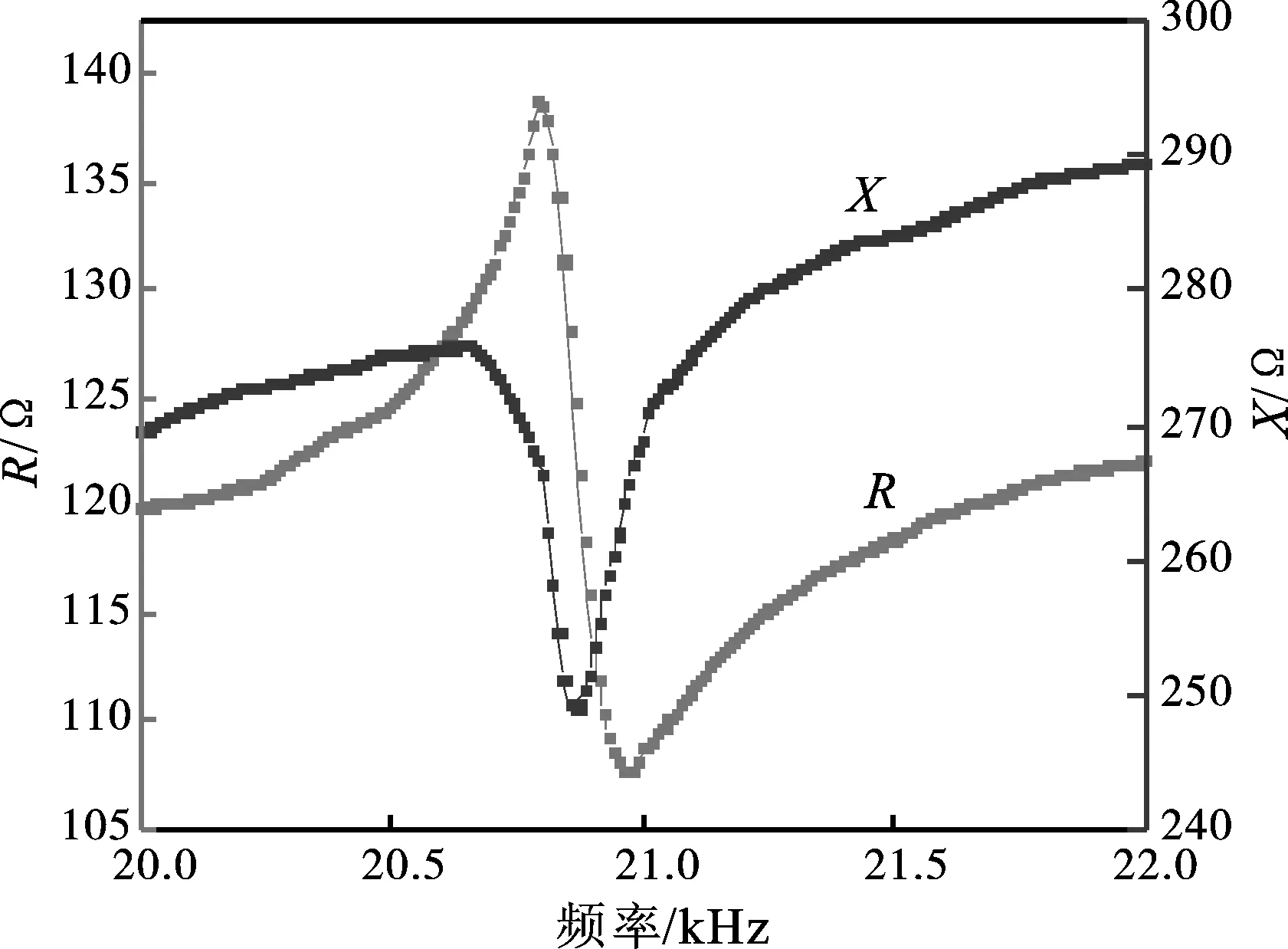
图5 换能器的阻抗曲线

表2为超磁致伸缩换能器理论计算、仿真模拟、实验测试的共振频率，一维纵向振动理论求得换能器的共振频率为fr，表观弹性法求得换能器的共振频率为fc，有限元仿真分析求得换能器的共振频率为fn，实验测量得到换能器的共振频率为fm，Δfr为一维纵向振动理论与实际测量求得共振频率的相对误差，Δfc为表观弹性法与实际测量求得共振频率的相对误差，Δfn为有限元仿真模拟与实际测量求得共振频率的相对误差。从表2中可以看出一维纵向振动理论求出换能器共振频率与实测值的误差为18.73%，表观弹性法求得换能器的共振频率与实测值的误差为0.22%，有限元法求得换能器的共振频率与实测值的误差为1.1%。基于一维纵向振动理论求出换能器的共振频率值与实际测量值误差较大，而表观弹性法计算得到换能器的共振频率与实际测量比较接近；这是由于一维振动理论要求换能器的横向尺寸远小于其纵波波长，当横向尺寸较大时，由于耦合振动的存在会产生较大的误差，而表观弹性法考虑了换能器的横向振动，计算所得到的结果与实际测量值更加接近。

表2 换能器的谐振频率

3 结论

本文利用有限元软件对稀土棒的涡流损耗进行分析计算，并基于解析法设计了一种超磁致伸缩换能器，利用表观弹性法得出换能器的等效弹性常数，对换能器的共振频率进行了计算；并对换能器进行动力学仿真分析；研制了超磁致伸缩换能器的样机，采用阻抗分析仪对换能器进行频率测试。得到以下结论：

(1)未处理稀土棒的涡流损耗外径表面大，内部小；与未处理棒相比，切片稀土棒的外径表面涡流损耗明显减小。切片处理GMM棒的涡流损耗比未处理GMM棒减小67.98%。

(2)基于一维纵向振动理论求出换能器共振频率与实验测值的误差为18.73%，表观弹性法求得换能器的共振频率与实验测值的误差为0.22%，根据表观弹性法计算的换能器共振频率与实验测量值比较符合。