斜槽式超声传振杆的纵弯复合振动及其等效电路

许 龙，陈一博

(中国计量大学 物理系，浙江 杭州 310018)

随着超声技术的发展，新的超声应用对超声振动能量的传播方式及作用形式提出了更高的要求。在超声线束焊接[1-2]、超声马达[3-5]、超声手术刀[6-8]以及超声振动切削[9-11]等技术中,纵弯复合振动具有更好的作用效果。目前，纵弯复合超声振动主要通过夹心式纵弯复合振动压电换能器[12-14]和纵弯模式转换超声换能器[15-17]产生。夹心式纵弯复合振动压电换能器利用两组压电陶瓷晶堆分别产生纵向振动和弯曲振动，当两种振动模式实现同频共振时振动系统进行纵弯复合振动[18]。纵弯模式转换超声换能器是在单一纵向激励作用下利用变幅杆结构上的不对称性，将该激励“分解”为两个相互垂直的响应，从而实现纵弯模式转换[19-20]；或者在纵向振动的变幅杆上，沿工具头进行横向激发，使其弯曲振动进而实现整个系统的纵弯复合振动[21]。

本文基于纵弯模式转换原理提出一种斜槽式超声传振杆，利用Euler-Bernoulli理论[22-23]推导了细棒弯曲振动T型等效电路和斜槽式超声传振杆纵弯复合振动机电等效电路，利用等效电路和有限元仿真得到了不同斜槽倾角时斜槽式超声传振杆纵弯复合振动的共振频率，通过两种方法所得共振频率的对比分析验证了等效电路模型的可靠性。进一步研究了斜槽式超声传振杆的斜槽位置和两斜槽间距对其纵弯复合振动模态的影响，以及斜槽长度和倾斜角度对其共振频率和输出端(右端)振动特性的影响。

1 斜槽式超声传振杆的结构和原理

图1为斜槽式超声传振杆的结构示意图，斜槽式超声传振杆为含有两个平行贯穿斜槽的圆柱形结构，圆柱的半径为R0，长度为L(L=L1+L2+L3，L1为斜槽左边部分长度，L2为斜槽的轴向长度，L3为斜槽右边部分长度)，A、B、C、D(A′、B′、C′、D′)为输出端面(输入端面)与圆柱外表面交界线上的节点，C″为CC′线段上的一个节点，位于斜槽左边部分和斜槽部分的交界面处。当在斜槽式超声传振杆的输入端(左端)施加纵向激励时，纵向振动传递到斜槽部分会因其结构不对称产生横向作用力，使斜槽右边部分产生弯曲振动，进而在斜槽右边部分产生纵向和弯曲的耦合振动。

图1 斜槽式超声传振杆的结构图

假定斜槽为宽度极窄的细缝，对斜槽式超声传振杆的质量无影响，斜槽仅起到将纵向振动转换为弯曲振动的作用。当斜槽式超声传振杆的输入端受到纵向力激发时，由于斜槽的作用整个超声传振杆产生纵向和弯曲复合振动。

2 均匀细棒弯曲振动的等效电路

对于均匀细棒的弯曲振动，若忽略剪切形变和转动惯量的影响，则可将均匀细棒简化为Euler梁，其弯曲振动波动方程为

(1)

式中：η为横向振动位移；K为截面回转半径；c2=E/ρ,E为杨氏模量，ρ为材料密度。利用分离变量法可得(1)式的通解为

η(t,x)=(Acoshλx+Bsinhλx+Ccosλx+Dsinλx)cos(ωt-φ)。

(2)

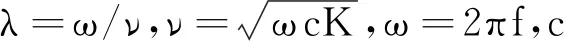
为了简化运算，引入符号S(λx)、T(λx)、U(λx)和V(λx),并且各函数之间关系满足dS/dx=λV、dT/dx=λS、dU/dx=λT、dV/dx=λU，其表达式分别为

(3)

将(2)式改写为Krylov函数

η(t,x)=[C1S(λx)+C2T(λx)+C3U(λx)+C4V(λx)]ejωt。

(4)

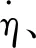
(5)

将式(4)代入均匀细棒边界条件式(5)，可得

(6)

(7)

式中，S1=πr2。由(6)式求解待定系数C1～C4为

(8)

将式(8)代入式(7)，可得细棒弯曲振动时横向作用力和横向振动速度的关系式为

(9)

式中：

(10)

根据(9)式，通过力电类比可得如图2所示的均匀细棒弯曲振动的T型等效电路。图2中：Za=Z1-Z2,Zb=Z2。

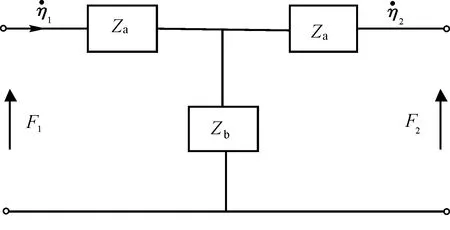
图2 均匀细棒弯曲振动等效电路

3 斜槽式超声传振杆的等效电路

斜槽式超声传振杆由斜槽左边等截面细棒、含斜槽细棒和斜槽右边细棒3部分组成，由于斜槽部分的斜槽宽度很小，可忽略其对振动系统质量的影响。当在斜槽式超声传振杆输入端施加纵向力激发时，纵向力经过斜槽会产生横向力分量，纵向和横向力的共同激励下斜槽右侧的传振杆产生纵弯复合振动。以斜槽部分和斜槽右边部分的交界面为纵向振动和纵弯复合振动的交界面，定义Nl为交界面处纵向振动与纵向振动之间的机械转换系数(纵纵机械转换系数)，Nt为交界面处纵向振动与弯曲振动之间的机械转换系数(纵弯机械转换系数)，Nl和Nt的表达式分别为

(11)

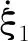
(12)

(13)

Zt1和Zt2为分界面右边部分弯曲振动的串并联阻抗，其表达式为

(14)

当斜槽式超声传振杆的输出端自由时，由传输线阻抗转移可得斜槽式超声传振杆纵弯复合振动的输入机械阻抗为

(15)

式中：Z′为斜槽右边部分纵弯复合振动的机械阻抗，其表达式为

(16)

式中：

HPLC法同时测定复方磷酸可待因口服溶液中3种有效成分及2种防腐剂的含量 ………………………… 魏文芝等（18）：2501

(17)

当斜槽式超声传振杆的输入机械阻抗为零时，由(15)式可得到其共振频率方程

Z0=0。

(18)

公式(18)中的共振频率方程与斜槽式超声传振杆的材料参数、几何尺寸、斜槽的位置和倾斜角有关。

4 模型验证

为了验证理论模型的可靠性，根据图1和表1所示结构尺寸利用有限元软件建立斜槽式超声传振杆的几何模型，并根据表1所示的7075硬铝材料参数定义几何模型的材料参数，选择固体力学模块并定义几何模型的初始条件和边界条件，通过特征频率计算可获得斜槽式超声传振杆的振动模态，如图4所示。在图4中，斜槽式超声传振杆的斜槽左边部分为纵向振动，右边部分为纵弯复合振动。

表1 斜槽式超声传振杆的几何尺寸及材料参数

图4 斜槽式超声传振杆纵弯复合振动模态

为了验证本文建立的斜槽式超声传振杆纵弯复合振动等效电路模型的精度，分别用等效电路法和有限元法计算了不同倾角斜槽式超声传振杆的纵弯复合振动的共振频率，如表2所示，其中fm1和fc1分别为等效电路法和有限元仿真所得共振频率，Δ1表示等效电路法与有限元仿真所得共振频率的相对误差，Δ1=|fm1-fc1|/fc1。

从表2可以看出，随着斜槽倾角的增加，理论和仿真计算所得共振频率的偏差逐渐增大，在斜槽倾角大于30°时，二者的相对误差达10%以上。其主要原因是利用Euler-Bernoulli理论推导细棒弯曲振动等效电路时忽略了剪切形变和转动惯量的影响，适用于小振幅的弯曲振动；当斜槽倾斜角度增大时，斜槽右边部分棒的弯曲振动振幅增大，由等效电路模型所得的共振频率误差也随之增大。因此，建立的斜槽式超声传振杆纵弯复合振动等效电路在斜槽倾斜角度较小时(即斜槽棒处于小振幅弯曲振动时)具有较高的计算精度。

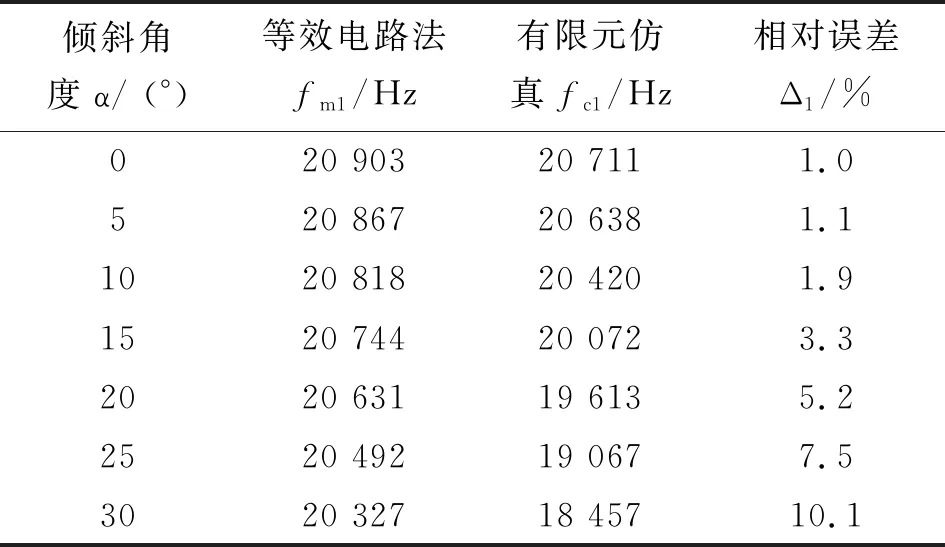
表2 等效电路法和有限元仿真所得斜槽式超声传振杆的共振频率及其相对误差

在建立斜槽式超声传振杆纵弯复合振动等效电路的过程中，引入了纵弯机械转换系数Nt，由Nt定义可知，Nt的大小与斜槽的倾角密切相关。利用有限元仿真计算了不同倾角的斜槽式超声传振杆的输入端纵向振动位移v1和输出端的横向振动位移η2，定义β为斜槽式超声传振杆的纵向与横向位移转换系数，β=η2/v1。纵弯机械转换系数Nt和纵横位移转换系数β随斜槽倾斜角度的变化关系如图5所示。

图5 纵弯机械转换系数Nt和纵横位移转换系数β随斜槽倾斜角度的变化关系

由图5可知，随斜槽倾斜角度α的增加理论模型引入的纵弯机械转换系数Nt和有限元仿真得到的纵横位移转换系数β变化趋势一致，由此可知理论模型引入的纵弯机械转换系数Nt很好地反映了斜槽棒的纵弯位移转换特性。由此表明，纵弯机械转换系数Nt和纵横位移转换系数β均可表示斜槽式超声传振杆纵弯转换能力的大小，具有正相关性。

5 振动性能分析

为研究斜槽式传振杆的振动性能，基于上述仿真模型在传振杆的输入端面施加频率20 kHz、振幅24.7 nm的轴向位移载荷(该位移载荷的振幅由实验测量换能器输出端的振幅所得)，利用瞬态动力学分析模块进行仿真计算。通过瞬态动力学计算，在第1.1 ms时传振杆输出端具有最大纵向及弯曲位移所对应的振型，传振杆的纵弯复合振动达到动态平衡状态。通过提取该振型下输出端面与圆柱外表面交界线上所有节点的横向位移，即图1中节点A、B、C、D所在圆上各节点的横向位移，可得图6所示传振杆输出端面与圆柱外表面交界线上各节点横向位移随其所在位置的变化规律。结合图6和图1，可知传振杆输出端节点横向位移在A、C点所在的位置最大，B、D点所在的位置横向振动位移最小。

图6 传振杆输出端面与圆柱外表面交界线上所有节点的横向振动位移

为了研究斜槽位置对斜槽式超声传振杆纵弯复合振动特性的影响，保持斜槽式超声传振杆总长度L不变，通过有限元软件的瞬态动力学模块计算了斜槽在不同位置时斜槽左边部分圆柱外表面C′C″线段上各节点的横向位移分布情况，其中斜槽位置以斜槽到超声传振杆左端面的距离L1为参考，结果如图7所示。在图7中，当L1=38.5 mm时斜槽式超声传振杆左边部分的横向位移最小，即受到斜槽式超声传振杆右边部分弯曲振动的扰动最小，此时斜槽式超声传振杆左边部分可看作纯纵向振动。

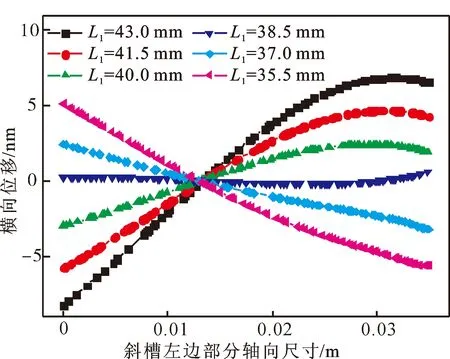
图7 斜槽左边部分横向位移分布

为分析斜槽式超声传振杆两斜槽之间的距离对其纵弯复合振动特性的影响，通过有限元仿真的瞬态动力学计算不同斜槽间距时传振杆在纵弯复合振动模式下圆柱外表面CC′线段上各节点的横向位移分布(如图8所示)，并提取了斜槽式超声传振杆输入端节点C的横向位移(如表3所示)。由表3和图8可知，随着斜槽间距的增加斜槽式超声传振杆输入端横向位移振幅先减小后增加，在斜槽间距为10 mm时具有最小值，表示在斜槽间距为10 mm时斜槽式超声传振杆左边部分受到右边部分弯曲振动的扰动最小，具有最佳的纵弯复合振动模态。

图8 斜槽式超声传振杆横向位移分布

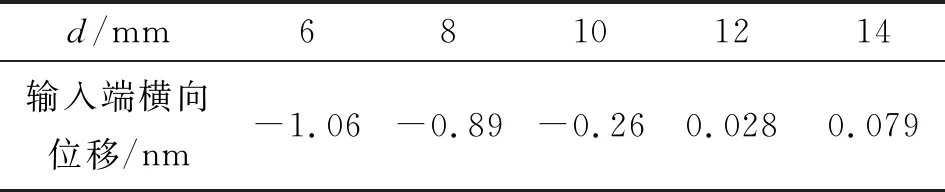
表3 斜槽间距对斜槽式超声传振杆输入端横向位移的影响

为分析斜槽的轴向长度L2和倾斜角度α对斜槽式超声传振杆纵弯复合振动特性的影响，在斜槽式超声传振杆长度L、斜槽位置L1和间距d不变的情况下，利用有限元仿真分析斜槽轴向长度L2(简称斜槽长度)和倾斜角度α对斜槽式超声传振杆共振频率和输出端横向与纵向振动位移之比的影响，结果如图9和图10所示。

图9 不同斜槽长度下斜槽式超声传振杆共振频率随斜槽倾斜角度的变化关系

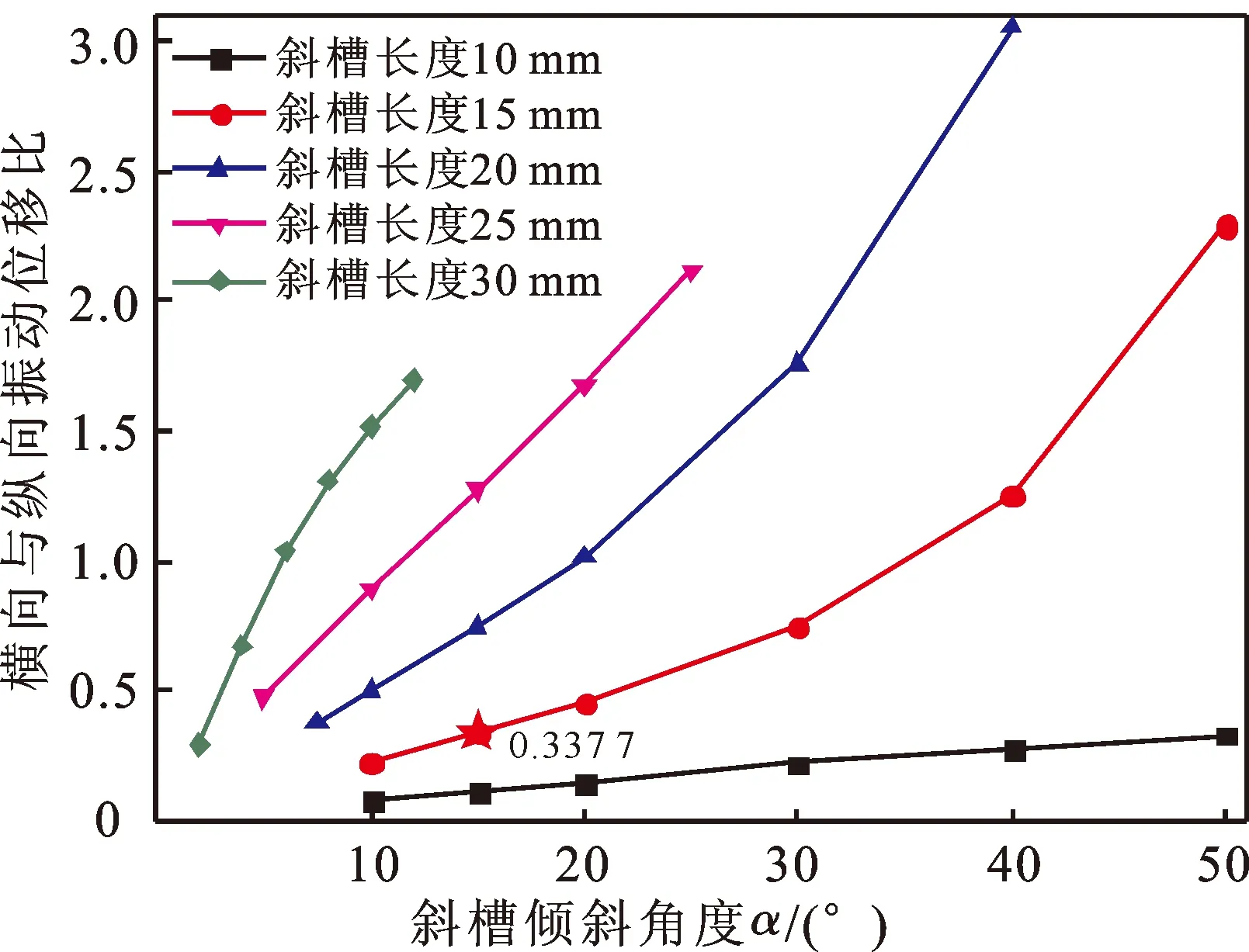
图10 不同斜槽长度下传振杆输出端横向与纵向振动位移之比随斜槽倾斜角度的变化

由图9可知，在同样的斜槽长度下斜槽式超声传振杆的共振频率随斜槽倾斜角度的增加而减小，而且随着斜槽长度的增加，斜槽式超声传振杆的共振频率减小速率变大，由此可知斜槽的长度和倾斜角度越大斜槽式超声传振杆的共振频率越小。由图10可知，在同样斜槽长度下斜槽式超声传振杆输出端横向与纵向振动位移之比随斜槽倾斜角度的增加而增加，而且随着斜槽长度的增加，斜槽式超声传振杆输出端横向与纵向振动位移之比的增加速率变大，由此可知斜槽的长度和倾斜角度越大斜槽式超声传振杆输出端横向与纵向振动位移之比越大。

斜槽式超声传振杆的斜槽长度和倾斜角度越大对其共振频率和输出端横向与纵向振动位移之比的影响越大，其主要原因是随着斜槽长度和倾斜角度的增加斜槽右边部分的横向分力逐渐增大，横向位移振幅也逐渐增大，横向振动对超声传振杆共振频率的影响也越大。

6 实验测试

根据表1所示斜槽式传振杆的几何尺寸选用7075硬铝材料加工了斜槽式传振杆的实验样品，如图11所示。为了测试斜槽式传振杆的纵弯复合振动特性，在斜槽式传振杆的左端连接20 kHz半波长夹心式压电超声换能器作为纵振动激励源，并对其施加峰值为20 V的激励电压，利用LV-S01激光测振仪测量斜槽式传振杆在纵振动激励下输出端节点C的纵向和横向振动位移，实验装置如图12所示(图12a为测量斜槽式传振杆输出端横向振动位移的装置，图12b为测量其输出端纵向振动位移的装置)。图13为实测的斜槽式传振杆输出端的横向和纵向位移-频率曲线。由图13可知，在频率为20 087 Hz时斜槽式传振杆输出端的横向和纵向位移具有最大值，分别为8.6 nm和23.8 nm，该频率对应于换能器及传振杆的纵弯复合振动共振频率，传振杆的横向与纵向位移振幅比值为0.36。通过与表2中倾斜角为15°时理论计算的传振杆共振频率(20 744 Hz)和有限元仿真的共振频率(20 072 Hz)对比，可知3种方法所得斜槽式传振杆的共振频率基本相同。通过对比实验测试和仿真计算的传振杆横向与纵向位移振幅比(分别为0.36和0.34，仿真计算结果参见图10红色曲线第二个计算点所示数值)，可知两种方法所得传振杆的输出端横向与纵向位移振幅之比非常接近。

图11 斜槽式传振杆的实验样品

图13 斜槽式传振杆输出端横向(a)和纵向(b)位移-频率特性曲线

为测试斜槽式传振杆在纵弯复合振动模态下的横向振动位移分布情况，并与图8所示的有限元计算结果进行对比，在斜槽式传振杆外表面沿线段CC′取13个测量点，测量步长为10 mm，利用LV-S01激光测振仪对每个点的横向位移振幅进行了测量,得到图14中斜槽式超声传振杆的横向位移振幅沿其轴向的分布(红色曲线)。为了将实验测试结果与图8中斜槽间距为10 mm的传振杆的有限元仿真结果比较，需要把有限元仿真所得的位移取绝对值，由此可得图14中传振杆的横向位移振幅沿其轴向的分布(黑色曲线)。通过对比可知，两种方法所得横向位移振幅分布基本吻合。

图14 斜槽式超声传振杆的横向位移振幅

7 结论

本文基于Euler梁弯曲振动理论和力电类比，通过引入斜槽式超声传振杆的纵弯机械转换系数，建立了斜槽式超声传振杆纵弯复合振动的等效电路模型并推导了其共振频率方程。通过对比等效电路法和有限元法所得斜槽式超声传振杆的共振频率，发现在斜槽倾斜角度小于30°时两种方法所得结果的相对误差较小,这表明本文建立的斜槽式超声传振杆纵弯复合振动等效电路模型在斜槽倾角较小时具有较高的理论计算精度。对斜槽式超声传振杆振动特性的仿真结果表明：当斜槽位置L1=38.5 mm和间距d=10.0 mm时，斜槽式超声传振杆具有最佳的纵弯复合振动模态；随着斜槽长度和倾斜角度的增加斜槽式超声传振杆的共振频率减小，输出端横向与纵向振动位移之比增大。基于理论分析模型，加工了倾角为15°的斜槽式传振杆，利用激光测振仪测试了斜槽式传振杆在纵弯复合振动模态下的横向与纵向振动位移，实验测试结果与仿真计算结果一致。