基于深度学习和导波阵列的高精度损伤成像方法

许伯强，邱彤彤，岳圣尧，徐晨光,，徐桂东，沈荣和，张 赛，3*

(1 江苏大学 超声检测研究所，江苏 镇江 212013；2 江苏大学 土木工程与力学学院，江苏 镇江 212013;3中北大学 省部共建动态测试技术国家重点实验室，山西 太原 030051)

板状或类板状结构广泛应用于航空、航天、高铁、船舶、风电等工程领域。此类结构在服役过程中经受集中载荷或外部冲击时容易产生微小损伤，若不及时发现则可能损伤累积而诱发重大事故。超声导波因在板状结构中具有传播距离远、能量衰减小、对结构表面和内部缺陷敏感等特点，使得基于超声导波的损伤检测技术受到无损检测(non-destructive testing，NDT)以及结构健康监测(structural health monitoring，SHM)领域研究学者和工程技术人员的广泛关注[1-4]。近年来，基于超声导波的阵列成像方法被广泛应用于NDT/SHM中，发展出多种阵列成像算法；然而，现有的阵列成像方法难以从阵列传感数据中有效提取损伤的微弱散射信息，无法准确表征损伤位置、程度及其类型，因而迫切需要发展能够重构损伤精细特征的成像方法。

在诸多基于超声导波的损伤成像方法中，相控阵时间延迟叠加成像(delay and sum beamforming，DAS)由于算法简单且能够实时重构成像而得到广泛应用。Habermehl等[5]用超声相控阵系统检测了飞机碳纤维增强聚合物基复合材料平板构件，结果表明该系统检测速度与成像效果优于传统超声检测手段；胡红波等[6]采用相控阵超声成像法对不同缺陷的钢筋混凝土叠合板试件进行检测，实现了对新旧混凝土结合面空洞、浮土等缺陷的有效检测。由于相控阵成像算法中的权重为事先确定，成像精度不理想，因而人们发展出相控阵全聚焦成像方法(total focusing method，TFM)。该方法充分利用增加的波场空间信息，实现成像空间分辨率和信噪比的提升[7-10]。Yu等[11]在超声导波相控阵板状结构件检测中，将导波波数-频率色散关系嵌入成像算法，有效提高了损伤成像精度；Liu等[12]提出了基于紧凑矩形相控阵压电换能器阵列的图像合成技术，可以将全聚焦图像与符号相干因子图像相结合得到复合图像，从而提高图像分辨率和对比度。

虽然TFM算法能够对被检测结构中存在的缺陷进行识别，但超声导波的非稳态、色散、多模态等特征[13-14]使得信号的损伤特征难以被准确获取，这给实际损伤高分辨率检测带来挑战。事实上，TFM方法的成像分辨率受衍射极限(Rayleigh准则)制约，理论上可实现的最小分辨率为1/2波长[15]。时间反转多信号分类(decomposition of time reversal operator-multiple signal classification，DORT-MUSIC)成像算法[16]可以实现亚波长高精度成像[17]。DORT-MUSIC算法对环境噪声条件要求高，且无法实现亚波长损伤特征(如缺陷尺寸、形状和类型等)的精确量化[18]。

深度学习(deep learning，DL)是一种多层神经网络方法，能够学习输入和期望输出之间的复杂关系，从而实现高维复杂数据间的非线性映射[19-20]。近年来，深度学习在图像高精度重构方面取得了诸多进展[21-23]。Umehara等[24]提出了基于DL的高精度卷积神经网络，用于增强胸部CT图像的分辨率，较好地恢复了两倍放大倍率下的原始成像结果，成像质量优于传统的线性插值方法；Sun等[25]为解决安全检查系统中单幅辐射图像空间分辨率低的问题，提出了基于DL的高精度重建方法，其量化指标和视觉效果较之传统的高精度重建方法均有较大改善，且具备较快的处理速度；Rasti等[26]以隐马尔可夫模型为基础，提出了基于DL卷积网络和奇异值分解原理的人脸识别系统，提高了监控摄像中人脸识别的精度。鉴于DL算法在医学图像处理、机器视觉领域中能够有效提升图像的精度和分辨率，研究者将DL方法应用于NDT和SHM中。Hu等[27]使用VGG-Net模型对压力容器的损伤定位进行了研究，指出DL方法具有良好的泛化能力和抗干扰能力；Shen等[28]为解决加筋板普遍存在的脱黏损伤检测问题，将卷积神经网络(convolutional neural network，CNN)与超声导波检测手段相结合，实现了对加筋板中脱粘损伤的有效检测；Song等[29-30]基于超声体波构建DL网络模型实现了损伤图像的高精度重现，突破了成像分辨率限制。

本文将导波阵列成像技术和深度学习相结合，在基于超声导波的TFM算法对损伤成像的基础上，将含损伤特征的低分辨率图像输入DL网络模型中，通过网络中分层级、多尺度识别以提取微弱的损伤精细特征，实现损伤的高精度成像，得到损伤大小和形状的细节特征。

1 全聚焦成像算法

TFM成像原理如图1所示。在待测板状结构中，设有N个导波激励阵元,当某个阵元i(1≤i≤N)激发时， 接收阵列中的M个采集点同时接收超声导波时域信号并存储，得到N列导波信号。然后依次单独激发每个阵元，即可得到M×L×N的三维超声导波时域信号,L代表每个采集点的时域采样点数。

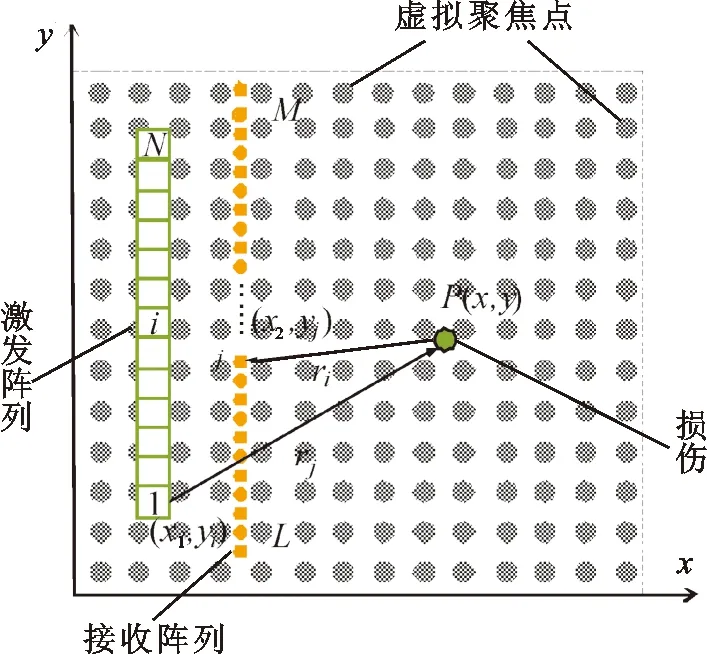
图1 板状结构中损伤TFM成像原理

P点为待测板状结构中任意一点，坐标为(x，y)。对时域信号Uij(ri,rj,t)施加延时量τ得到该点延时后的信号Uij(ri,rj,t+τ)，将所有激励-接收阵元对的延时信号同相位叠加获得P点信号增强后的像素强度为

(1)

式中：i代表发射阵元；j代表接收阵元；x1和x2分别为发射阵元和接收阵元的横坐标；yi和yj分别为发射阵元和接收阵元的纵坐标；cg是激励信号中心频率下的导波群速度。像素强度I与缺陷的特征直接相关。TFM成像过程中，通过傅里叶变换将所有接收的导波时域信号转变到频域，基于相干叠加得到场点P处导波的强度幅值，最终得到图像的强度分布，实现对损伤的评价。

通过数值模拟和实验，对含有单圆形通孔损伤的铝板进行TFM成像，结果如图2所示。将数值模拟下的TFM成像结果(图2b)与DAS成像结果(图2a)对比可以发现：前者具有更高的成像精度和空间分辨率；与实验数据TFM成像结果(图2c)相比，数值模拟下的DAS成像结果热点区域面积少，但定位偏移，成像精度仍然较低。因此，本文选用TFM成像结果为DL网络的原始数据集。

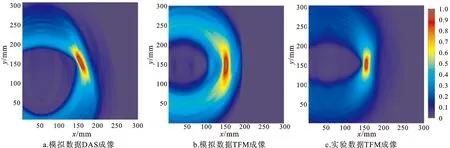
图2 铝板结构单孔成像结果

1.1 数值模拟获取数据

基于COMSOL Multiphysics有限元软件，建立含典型损伤的铝板结构中超声导波激励/传感数值分析模型，如图3所示。其中，铝板的厚度为1 mm，杨氏模量为7×1010Pa，泊松比为0.33，密度为2 700 kg/m3。在待测区域的周围设置宽度为30 mm的阻尼层以消除边界反射波的干扰，并设置圆孔和裂纹两种损伤，圆孔的半径变化范围为2～6 mm；裂纹长度变化范围为8～15 mm，宽度变化范围为0.5～1 mm，损伤位置随机。高分辨率成像方法由图3展示，利用中心间距为10 mm的11个压电片阵列激励超声导波，中心间距为1.5 mm的100个纵向采集点获取损伤散射信号。

图3 数值模拟模型

为了激励超声导波，本文采用中心频率为fc=100 kHz的脉冲调制信号f(t)作为激励信号

(2)

由铝板频散曲线(见图4)可知，中心频率为100 kHz的A0模态导波的相速度为cp=1 761 m/s，其对应的波长约为17 mm，远大于所设置的圆孔和裂纹尺寸。

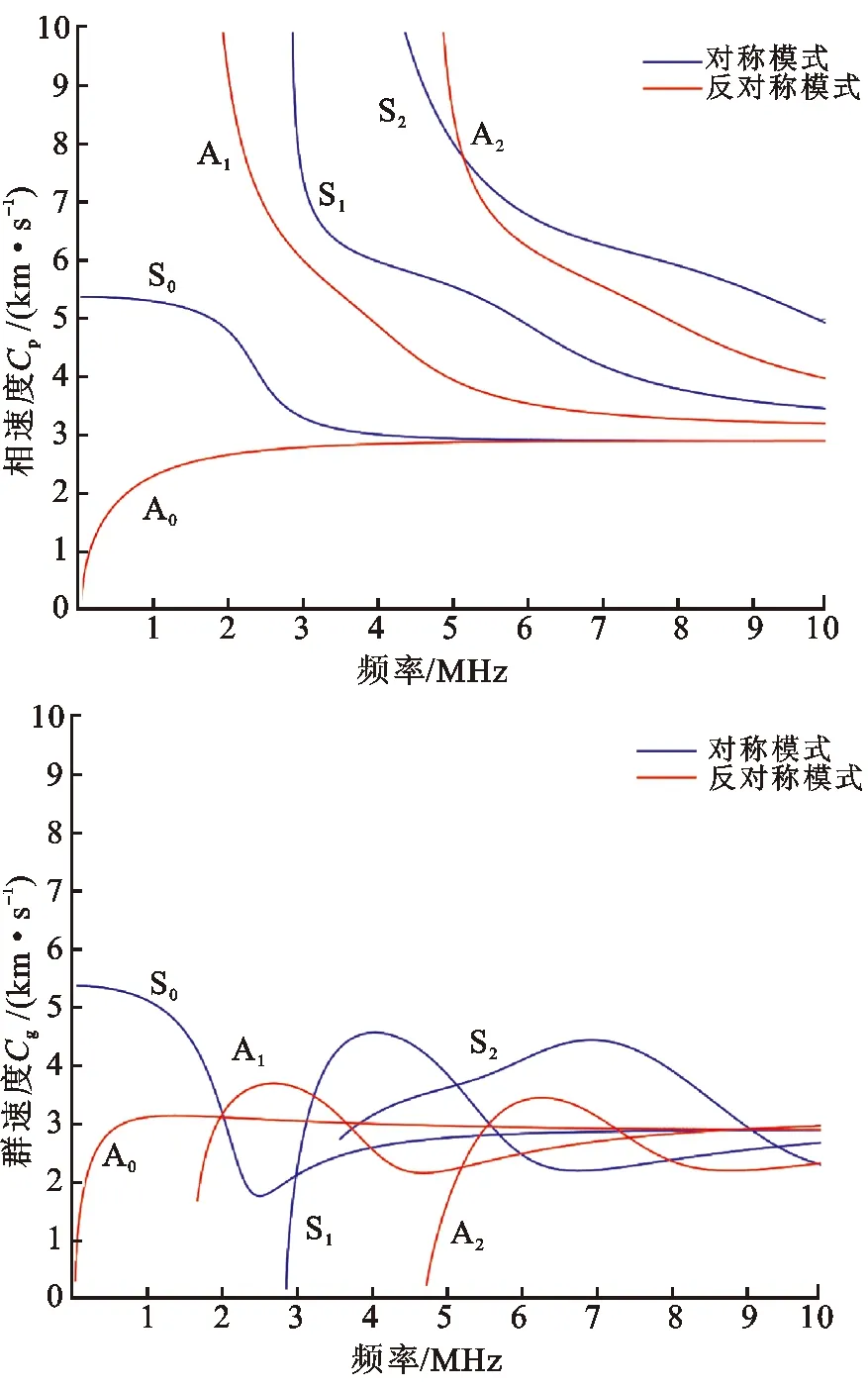
图4 1 mm厚铝板的频散曲线

1.2 实验获取数据

超声导波阵列损伤成像实验系统如图5所示，选用尺寸为500 mm×500 mm×1 mm的铝板作为试样，设有半径为5 mm的双圆形通孔损伤。实验中，将11块PZT贴片(单个尺寸为10 mm×10 mm×0.2 mm)以10 mm的中心间距均匀黏接在铝板上，依次激励PZT用于产生超声导波,激光多普勒测振仪(scanning laser doppler vibrometer，SLDV)沿中心间距为1.5 mm的100个纵向采集点同时接收损伤散射导波信号，形成阵列数据用于后文TFM成像。受SLDV仅能测量板的离面速度的影响，采集数据的主要成分为A0波，采样频率设为5.12 MHz，单次采样时间为400 μs。

图5 实验系统及待测样品

1.3 数据库配置

神经网络的良好训练需要大量数据作支撑，本文所需的TFM图像可以通过数值模拟或实验获得。数值模拟所得图像噪声低，精确度高，但耗时较长；实验方法效率相对更高，但需要大量实验样品，成本高，且易受环境噪声干扰，成像效果相对较差。因此，本文采用数据增强的方法来获得合理且大量的训练数据。

图6给出了本文采用的图像数据生成和增强方法，使用Python图像标签工具Labelme将TFM算法获得的全尺寸超声阵列图像剪裁为64×64像素级标签损伤，经过水平翻转、随机角度旋转、对比度调整、随机尺度放大与缩小等策略最终实现数据库扩充。

图6 图像数据生成和增强策略

通过数值模拟和实验获得的TFM成像图片分别为175张和50张，经过数据增强的操作得到仿真数据的成像结果为10 040张，实验数据的成像结果为2 510张。为了验证高分辨率网络性能，本文设置3种不同的训练与检测方案，如表1所示。

2 深度学习神经网络模型

如图7所示，本文中网络架构以经典的U-Net[31]为基础，采用修正线性单元(rectified linear unit，ReLU)作为激活函数，设置编码层和解码层，以获取损伤的精细特征。网络的编码层由5个卷积模块组成：模块1包含1个1×1卷积层和2个3×3卷积层，模块2仅包含2个3×3卷积层，而模块3～5均含有3个3×3卷积层。模块1～4卷积结束时均进行2×2的最大池化(Maxpool)操作。网络解码层中的4个反卷积模块构成为：1个2×2反卷积层、1个连接层、1个1×1反卷积层和2个3×3卷积层。此外，为了在加速网络收敛的同时避免过拟合现象的发生，在每一次卷积与反卷积之后均添加了相应的批量归一化(batch normalization，BN)[32]操作。

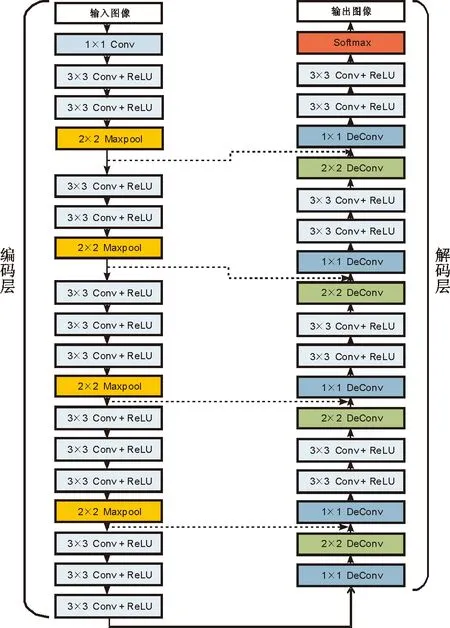
图7 高精度网络的架构

2.1 网络运行过程内视

为了更好地理解网络运行过程中图像特征的变化，本文针对性观察了每个层的输出。通过检测过程的可视化分析，不仅可以展示损伤图像的实际物理性质，并且演示了网络消除导波色散多频率特征的整体过程。

选取裂纹损伤图像进行可视化分析，如图8所示，其中裂纹损伤长9 mm、宽0.5 mm，顺时针偏移垂直位置30°。本节仅对解码层进行可视化操作，并融合展示不同模块下卷积与反卷积的操作结果，以此突出网络学习过程中特征“恢复-抓取-再恢复”。通过图8可以看出，随着反卷积模块运算次数的增加，对于损伤细节特征的抓取与恢复，因色散引起的负面影响不断消除，网络输出图像的分辨率不断增高。

图8 网络检测过程的可视化

2.2 网络模型功能分析

2.2.1 多尺度分析抓取散射信号微弱特征

卷积运算因在图像分类中的高有效性与高可靠性而被广泛应用于深度学习之中，通过多次卷积操作的累加可以构成网络的编码层，能够实现损伤信息的压缩与多维度特征的提取。通过大小为k×k的卷积对w×w大小的图像进行处理，卷积后特征图的宽度为

(3)

卷积层运算进行特征提取的原理如图9所示。假设图像的某一特征A(损伤)包含多个维度的特征(A1～A4：损伤的形状、位置、大小及类型等)，将图像输入卷积层，多个数量级的卷积核同时工作，以对其不同维度的特征进行抓取，再经过池化操作使得不同维度的特征精炼整合。每一次的卷积和池化都是一次不同尺度特征的提取，通过多次卷积和池化操作不断对获取的特征进行抓取与提炼，最终实现针对图像多尺度特征的压缩与抓取。

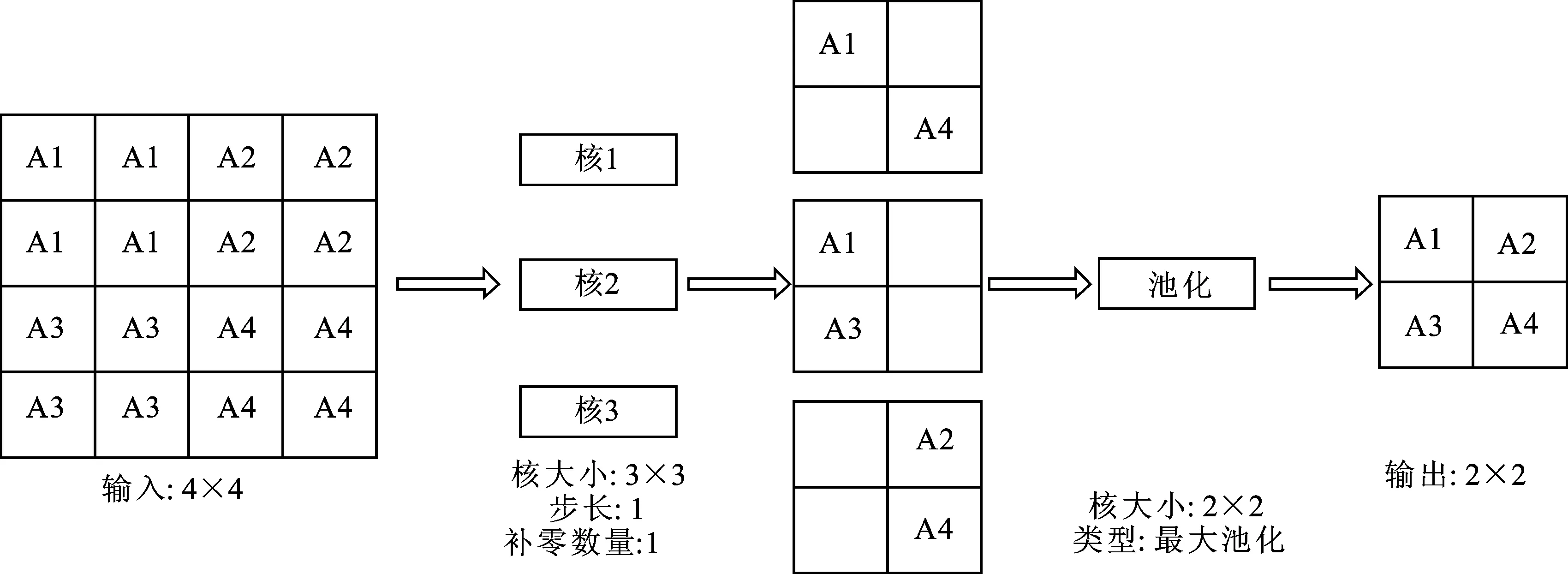
图9 卷积运算特征提取

多次反卷积操作累加构成网络的解码层，反卷积后特征图的宽度为

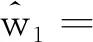
(4)

式中,w1是图像输入宽度。

通过反卷积层运算来重构特征的原理如图10所示，可以从接收到图像的已提取特征A中重构和恢复深层次的损伤特征信息，使图像以更高的分辨率显示损伤细节。每一次的反卷积都是不同尺度特征的恢复，通过多次反卷积操作不断对已获取的特征进行恢复，最终可以完成图像多尺度特征的恢复，从而实现高精度成像。

图10 反卷积运算特征恢复

单一尺度的卷积或反卷积并不能实现对多维且复杂板结构损伤特征的高分辨率提取与恢复，因此网络的编码层与解码层需包含不同尺度的卷积与反卷积操作，以抓取不同分辨率的特征，进而实现高分辨率特征的还原。同时，为了维持每一次卷积与反卷积操作后的尺度不变性，本文在网络编码层中添加了1×1卷积层，在解码层中添加了1×1反卷积层；该操作极大程度地抓取了连续降维和升维计算过程中的图像特征，减少了编码解码过程中必要信息的丢失，丰富了网络捕获信息的多尺度性。

2.2.2 非线性增强

含损伤信息的TFM成像包含损伤的多维度和多尺度精细信息，但噪声、频散等因素的存在导致该类精细信息无法有效提取。1×1卷积与1×1反卷积操作除了能保持图像尺度不变之外，也能够分别增加或减少数据通道维数，因而本文在经典U-Net中增加了1×1卷积和1×1反卷积层。反卷积增加数据特征维数，并通过非线性ReLU激活函数来增加非线性特征的提取。这样，输入的低分辨率(low resolution，LR)图像通过卷积与反卷积操作后，就能从原始低分辨率的损伤图像中提取出微弱的损伤精细特征，进而实现损伤的高精度成像。

2.2.3 分层级特征融合增强

在使用网络对图片特征进行抓取与恢复的过程中，浅层卷积包含分辨率较高的特征与丰富的低层级信息，但特征宽泛，不具代表性；而高层卷积则包含抽象且分辨率较低的特征，但特征聚焦程度较高。通过“跳连”可以把不同层级卷积的特征相互联系，即从编码层获得的某些特征会被直接映射融合到解码层中。解码层中的每一个反卷积会对每一次融合学习后的特征进行反卷积的操作，这将更有利于获取图片不同层级的维度信息，最终实现对多特征图像的高分辨率重建。为了实现损伤细节化特征的分析，在图7所示的编码层和解码层之间构造多个 “跳连”操作。

2.3 网络参数配置

2.3.1 损失函数

损失函数的选择极大地影响网络的训练成果，而一般深度学习卷积网络常用的均方误差(mean square error，MSE)易丢失高频细节特征[33]，并不适用于板状结构精细损伤的高分辨率成像。因此，本文选择Dice Loss[34]函数作为优化的损失函数，其表达式为

(5)

式中:Li是标签图像第i个像素的标签值;Pi是预测输出图像第i个像素有缺陷的预测概率;Np是标记和预测图像的像素总数。该函数的应用可以有效减少预测图像集和真实高分辨率图像集之间的误差，当测试值与标签值的相似度越高时，Dcoeff越趋近于1，损失函数LDice则越趋近于0。

值得一提的是，Dice Loss函数在训练过程中更侧重于对正样本区域的挖掘[34]，与导波损伤高分辨率成像工作中正样本区域(损伤区域)[35]和负样本区域(背景区域)面积占比存在严重不平衡的情况十分匹配。针对不同输入面积的训练图片，正样本区域的面积总是为固定值，这使得针对正样本区域计算的损失值不变，其对网络的监督贡献不会随着输入图片的大小而改变，具有较好的鲁棒性。

2.3.2 超参数选择

损失函数确定后，配置好用于训练和验证的数据集，图7中的高精度网络将接受训练以找到多层网络结构的最优权值，从而使损失函数最小化。表2给出了用于训练高精度网络的参数。

表2 用于训练高精度网络的超参数

2.4 训练结果与网络性能

2.4.1 网络训练结果

训练集、验证集的损失值和精度值曲线如图11所示，其中蓝线是训练集的变化，橙线是验证集的变化。通过整体曲线走势可以看出，损失值随着训练次数的增加逐渐降低，而精度值逐渐上升，两者最终均趋于稳定。

图11 方案1/2和方案3的损失曲线和精度曲线

网络训练结果如表3所示。方案3中训练集的损失值比方案1/2低0.03，验证集的损失值比方案1/2低0.02，而精度值分别高0.03和0.02；这说明对于方案3的混合数据，训练过程趋于平滑的速度更快，且损失值更小，精度值更高。

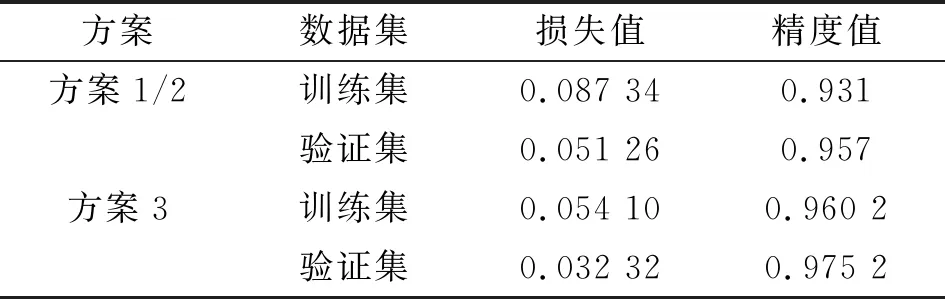
表3 不同方案的网络训练结果

2.4.2 网络性能评价

本文使用类别平均像素准确率(mean pixel accuracy，MPA公式中用VMPA表示)和平均交并比(mean intersection over union，MIoU公式中用VMIoU表示)2个评价标准来表征评价指标。

像素准确率(pixel accuracy,PA)是识别区域内正确分类的像素值在该区域内总像素值中的占比，表示在测试含损伤的测试集时，针对每个类的像素识别结果的正确率。MPA是所有PA的平均值，MPA越趋近于1，网络性能越好,即

(6)

交并比(intersection over union,IoU)是识别区域与理想区域的交集像素与识别区域与理想区域的并集像素的比值，表示在测试含损伤的测试集时，针对正确识别区域内像素的精准度。MIoU是所有IoU的平均值，MIoU越趋近于1，网络性能越好，即

(7)

式中:pii代表模型预测为损伤、实际是损伤的数量；pij代表模型预测为损伤、实际是背景的数量；pji代表模型预测为背景、实际是损伤的数量；pjj代表模型预测为背景、实际是背景的数量。

表4给出了不同方案的MIoU和MPA指标值，3种方案评价指标均接近于1，显示出较好的网络性能。特别是对于方案2，与完全使用模拟数据的研究相比，对仅使用仿真数据训练的网络进行部分实验数据的检测(实验数据为随机抽取)，其MIoU和MPA值仅比方案1分别低0.3%和0.4%，这表示所提出的网络具有良好的训练和检测精度。

表4 不同方案的MIoU和MPA

3 深度学习网络模型验证

3.1 成像结果精度验证

首先验证圆孔-裂纹缺陷图像精度，圆孔损伤半径为2 mm，裂纹损伤长度为15 mm、宽为1 mm。如图12所示，将通过数值模拟所得的TFM成像结果(图12a)送入高分辨率成像网络中，得到DL网络输出结果(图12c)，其中损伤成像区域为黑色阈值区域，两种损伤的实际位置和大小如图12a中白色圆圈和矩形所示。此外，本文将成像结果中心区域点(即色阈值最高的点)与真实成像结果中心区域点的直线距离作为定位指标。针对圆孔损伤，与TFM成像结果相比，DL网络输出结果热点区域面积降低23%，损伤定位精准率增高7%；与真实成像结果(图12b)相比，损伤定位点的像素相交率超过95%，相对误差缩减至1 mm以内。针对裂纹损伤，与TFM成像结果相比，DL网络输出结果热点区域面积降低32%，损伤定位精准率增高5%；与真实成像结果相比，损伤定位点的像素相交率超过91%，相对误差缩减至1.2 mm以内。

图12 圆孔缺陷和裂纹缺陷模拟数据的高精度成像可视化结果

进一步验证圆孔-圆孔缺陷图像精度，2个圆孔半径均为3 mm。将通过数值模拟所得的TFM成像结果(图13a)送入高分辨率成像网络中，得到DL网络输出结果(图13c)。针对位于上方的圆孔损伤，与TFM成像结果相比，DL网络输出结果热点区域面积降低28%，损伤定位精准率增高5%；与真实成像结果(图13b)相比，损伤定位点的像素相交率超过92%，相对误差缩减至1.1 mm以内。针对位于下方的圆孔损伤，与TFM成像结果相比，DL网络输出结果成像热点区域面积降低35%，损伤定位精准率增高4%；与真实成像结果相比，损伤定位点的像素相交率超过98%，相对误差缩减至1.5 mm以内。

图13 2个圆孔缺陷实验数据的高精度成像可视化结果

结果表明，TFM成像算法并没有考虑两个相近圆孔缺陷散射导波的干涉效应，而通过深度学习的非线性增强算法可以分辨损伤的亚波长特征。经过本文所搭建的DL网络模型可以生成缺陷的高精度图像结果，以表征形状和大小等精细特征。

3.2 网络鲁棒性验证

针对原始信号分别添加60 dB和10 dB 2种噪声来进行初始成像后再送入高精度成像网络，以此验证模型的抗噪能力。实验总共形成300张不同信噪比的损伤图像，选用方案3对添加噪声的数据集进行测试，结果如表5所示。

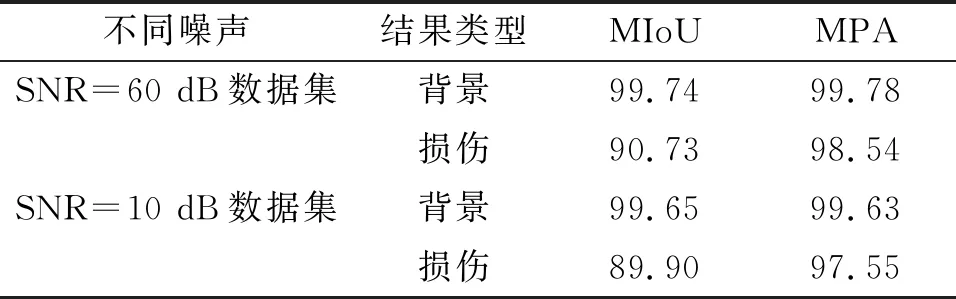
表5 不同信噪比测试集的MIoU和MPA

对比表4和表5数据，60 dB SNR数据集的检测结果与原方案3相同；而10 dB SNR数据集检测结果中的MIoU值比原方案3低0.83%，MPA值比原方案3低0.99%。这表明针对不同信噪比的数据集，其检测结果的指标值基本一致，即本文提出的高精度检测网络抗噪能力强，具有极好的鲁棒性。

以双圆形通孔损伤图像为基准，添加不同信噪比后的成像结果如图14所示。其中图14a与图14c分别为SNR=10 dB和SNR=60 dB的初始成像结果，图14b与图14d为对应的DL模型的输出结果，尽管初始输入的TFM成像结果受不同噪声影响，但最终经过DL网络输出图像结果基本相同，这再次验证了本文所搭建的网络模型对随机噪声具有鲁棒性，可以有效表征所识别缺陷的尺寸、形状等特征。

图14 不同信噪比成像结果

4 结论

本文在阵列导波TFM损伤成像基础上，基于深度学习发展了板状结构亚波长圆孔和裂纹损伤的高精度成像方法，以定位亚波长损伤的尺寸和形状。通过数值模拟和实验对板中损伤的亚波长成像进行研究，建立了用于不同方案下的数据库。本文所提方法在训练过程中最终训练误差值低于0.08，精度值高于0.93，表明网络训练收敛性较高，能够抓取和学习数据库中与损伤相关的特征，并且对阵列数据中的随机噪声具有较强的鲁棒性。

深度学习网络模型生成的高精度成像结果表明，多尺度算法能够针对损伤的细节特征进行抓取，非线性增强模块能够有选择地提取损伤散射的微弱信号，分层级融合算法能够融合不同的损伤点形成损伤的形状。该方法能够实现板状结构中亚波长损伤的高精度成像和分析，为智能超声导波损伤检测方法提供了理论依据和新思路。