一种新的直觉模糊最小二乘支持向量机
2022-12-01周水生张文梦
张 丹,周水生,张文梦
(西安电子科技大学 数学与统计学院,陕西 西安 710126)
支持向量机(Support Vector Machines,SVM)作为处理二分类问题的一种重要方法,已被广泛应用于各个领域[1-4]。不同于传统的支持向量机,最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM)是基于一组等式约束提出的,只需通过求解一个线性方程组即可得到闭式解,而不是求解一个对偶的二次规划问题[5],从而加快了训练速度。目前,LSSVM已广泛应用于模式识别[6]、故障诊断[7]、图像分类[8]和偏微分方程求解[9]等领域。然而,LSSVM易受离群点和噪声的影响。为了解决离群点和噪声对LSSVM的影响,SUYKENS等[10]提出了加权最小二乘支持向量机(Weighted Least Squares Support Vector Machines,WLSSVM),通过为每个样本点分配不同的权值来降低影响,提高模型的鲁棒性。YANG等[11]提出了一种鲁棒的最小二乘支持向量回归机(Robust Least Squares Support Vector Machines,RLSSVM),该方法同时最小化全局模型误差的方差和均值,实验表明可以有效降低噪声对模型的影响。MA等[12]提出了一种新的鲁棒最小二乘支持向量分类器(Robust Least Squares Support Vector Classifier,RLSSVC),通过最小化各类模型误差的均值和方差来提高分类器的鲁棒性。CHEN等[13]将最小二乘损失函数换成截断损失函数,提出稀疏的鲁棒最小二乘支持向量机(Sparse Robust Least Squares Support Vector Machines,SRLSSVM)降低了噪声的影响,提高了模型的鲁棒性。此外,LIN等[14]首次提出了模糊支持向量机(Fuzzy Support Vector Machines,FSVM),为每个样本点赋予不同的隶属度值,使不同的样本点对最优分离超平面有不同的贡献。通过对离群点和噪声赋予低的隶属度,降低了离群点和噪声对分离超平面的影响。对于FSVM算法,其关键问题是如何设计隶属度函数。对于隶属度的确定,TANG[15]提出了一种新的模糊函数,通过计算一类的样本点到另一类样本点边界的距离,有效地区分支持向量和噪声。BATUWITA等[16]提出基于三种距离的线性和指数模糊函数,并将其用于不平衡数据的分类。LIU[17]在此基础上提出了新的高斯模糊函数,实验表明,其分类效果良好。TAO等[18]基于空间一致性原则提出了基于亲和力和类概率的模糊支持向量机,可以有效减小离群点和噪声对模型的影响。FAN等[19]通过计算样本的高阶类概率提出了基于熵的模糊支持向量机,利用样本点熵的信息来确定样本点的隶属度。然而,上述模糊值的提出,均基于样本点对其所在类的隶属程度,未考虑样本点与另一类的关系。
为了更加细致地刻画样本点的不确定程度,ATANASSOV[20]提出了直觉模糊集,包含了样本点的隶属度、非隶属度及犹豫度三方面信息。哈明虎等[21]基于直觉模糊集提出了直觉模糊支持向量机,通过样本的分布特征确定样本的隶属度和非隶属度,将样本直觉模糊化,再利用支持向量机对直觉模糊化的样本进行分类。在直觉模糊支持向量机中,样本点对最优分离超平面的贡献由直觉模糊集的两个参数(隶属度和非隶属度)给出,从而在一定程度上减少了噪声和离群点的影响。HA等[22]提出了一种新的基于直觉模糊集和核函数的模糊支持向量机(Intuitionistic Fuzzy Support Vector Machines,IFSVM),对处理离群点和噪声问题表现优越。REZVANI等[23]将直觉模糊数引入双支持向量机模型,得到直觉模糊双支持向量机。该方法根据样本点的得分函数来评价样本点对分离超平面的贡献,这种方法可以区分支持向量和噪声,改进了传统的基于样本点类中心的模糊支持向量机将支持向量赋予低的模糊值的缺点。上述直觉模糊数的给出方式可以很好地减少噪声和离群值的影响,但是也有其不足之处。计算隶属度时,类中心是基于所有样本点计算的,而离群点可能会导致类中心偏移;非隶属度的计算依赖参数的选取,对于分布稀疏的样本点,若半径选取不合适,则会造成计算不准确。
针对上述问题,基于直觉模糊集,笔者提出了新的隶属度函数和非隶属度函数来确定样本点的直觉模糊数。通过更新样本点的类中心与球面减少离群点的影响,使得隶属度更加准确,同时采用核k近邻方法计算非隶属度函数,避免了邻域内样本点稀疏导致样本点非隶属度不准确的问题。然后根据隶属度与非隶属度计算得分函数来为样本点分配模糊值,通过对离群点和噪声赋予很低的模糊值来降低其对分类模型的影响。进一步将提出的新的模糊值用于LSSVM模型,用来减少离群点和噪声对LSSVM的影响,从而提升模型的鲁棒性。
1 相关知识
1.1 最小二乘支持向量机
(1)
其中,ξi是第i个样本的误差,φ(xi)是一个将xi映射到高维特征空间的非线性函数,C是惩罚因子。
通过求解Karush-Kuhn-Tucker(KKT)条件可以得到如下线性方程组:
(2)
其中,I∈Rl×l是单位阵,e=(1,1,…,1)T是分量为1的矩阵,Y=(y1,y2,…,yl)T表示标签向量,Z=[φ(x1)Ty1,…,φ(xl)Tyl]T表示特征矩阵与标签的乘积,α=(α1,α2,…,αl)T是拉格朗日乘子。通过求解式(2)可以得到问题的解:
(3)
1.2 直觉模糊支持向量机
1.2.1 直觉模糊集
定义1设X是一个非空集合,则称下式为模糊集[20]:
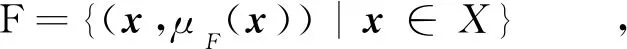
(4)

定义2设χ是一个给定论域,则χ的一个直觉模糊集[20]定义为
A={(x,μA(x),νA(x))|x∈X} ,
(5)
其中,μA(x)和νA(x)分别为x∈X的隶属度函数和非隶属度函数,其中μA∶X→[0,1],νA∶X→[0,1]且有0≤μA(x)+νA(x)≤1成立。x∈X的得分函数[22]可以定义为
(6)
隶属度函数体现了x对集合X的隶属程度,隶属程度越高,隶属度越大;非隶属度函数体现了x不属于集合X的程度。在处理分类问题时,隶属度通常指样本点对其所在类的隶属程度,体现了样本点与所在类的关系;非隶属度通常用样本点与其他类的关系来体现样本点不属于其所在类的程度。得分函数利用样本点的隶属度与非隶属度值给出了样本点的分数值,可以用来比较同一类中不同样本点的隶属程度。
1.2.2 直觉模糊支持向量机
(1) 隶属度函数定义为
(7)
其中,δ>0为参数,r+、r-和C+、C-是正负类点的半径和类中心。
(2) 非隶属度函数衡量了样本点邻域内异类样本点与邻域内所有样本点的关系,其定义为
ν(xi)=(1-μ(xi))ρ(xi) ,
(8)
并满足0≤μ(xi)+ν(xi)≤1,且ρ(x)定义为
(9)
其中,τ>0是参数。
根据样本点的隶属度和非隶属度函数,定义其得分函数为
(10)
基于上述直觉模糊值的支持向量机模型为
(11)
其中,ξi是第i个样本的误差,φ(xi)是一个将xi映射到高维特征空间的非线性函数,C是惩罚因子。
在上述隶属度的定义中,样本点的类中心是基于所有样本点来计算的,受离群点的影响,得到的类中心可能是不准确的。在计算大多数样本点的类中心时,应考虑离群点的影响。计算样本点的非隶属度时,对于分布稀疏的样本点,若邻域半径τ选取过小,则会导致邻域内样本点数量较少,计算得到的非隶属度不准确。
1.3 现有的模糊函数及其局限性
在已有的研究中,定义了很多经典的模糊函数,如文献[16-17]中提出的3种模糊函数:
(12)
(13)
(14)
对于距离也有不同的定义方式,如在文献[16]中介绍了3种距离:① 样本点到自己类中心的距离,记为dcen;② 样本点到预估分离超平面的距离,记为dsph,预估的分离超平面是所有样本点的中心;③ 样本点到分离超平面的距离,记为dhyp,该距离先训练一次传统的支持向量机,再计算样本点到分离超平面的距离。
这些模糊函数的提出有一定的局限性:
(1) 上述模糊值是基于距离给出的,但是相同距离的训练样本点对分离超平面的贡献不一定相同,因此仅基于距离提出的模糊值不能准确描述训练样本点对其所在类的隶属度。
(2) 基于到样本点类中心的距离得到的模糊值可能是不准确。样本点的类中心是基于该类所有的样本点计算的,受离群点的影响,得到的类中心不一定是准确的,因此用该类中心的距离计算的模糊值也可能是不准确的。在计算类中心时,应尽可能避免离群点的影响。
(3) 上述模糊值的给出都是在样本点的输入空间,模糊值描述了样本点在输入空间中的数据特征,而分类时往往是在高维空间中进行,将输入空间中得到的模糊值用于高维空间分类是不合理的。根据空间的一致性原则,应利用样本点在高维空间中的数据特征给出模糊值,再在高维空间中进行分类。
由上述分析可知,已有的模糊值函数并不能很好地描述样本点的分布信息。为此笔者提出一种新的直觉模糊最小二乘支持向量机,结合样本点隶属度与非隶属度信息,赋予样本点更为合理的模糊值,从而提高分类准确率。
2 一种新的直觉模糊最小二乘支持向量机
给出了样本点的隶属度函数与非隶属度函数,再根据其得分函数给出最终模糊值,并将其用于改进LSSVM模型,得到一种新的直觉模糊最小二乘支持向量机(New Intuitionistic Fuzzy Least Squares Support Vector Machines, NIFLSSVM)。
2.1 直觉模糊数
为了减少离群值和噪声对模型的影响,选择合适的模糊函数是至关重要的。现有的模糊值大多是基于样本点的隶属度函数给出的,未考虑样本点的非隶属度。基于直觉模糊集给出了描述样本点与所在类的关系隶属度函数和样本点与其他类的关系非隶属度函数,根据其得分函数得到最终直觉模糊数。此外,基于空间一致性原则,在高维空间中给出样本点的直觉模糊数。
2.1.1 隶属度函数
隶属度函数通常用于衡量样本点对其所在类的隶属程度,隶属程度越高,隶属度的值越大。隶属度函数的计算往往需要利用样本点到其类中心的距离及其所在类的半径。目前,对于类中心和类半径的计算大多是基于所有样本点的,得到的球面包含了所有样本点。但是受离群点和噪声的影响,类中心和类半径的值可能是不准确的,从而计算得到的隶属度也可能不准确。因此在计算类中心和类半径时,可以考虑大部分样本点的类中心和类半径,以减少影响。因此通过更新样本点的类中心和类半径,可以得到包含大部分样本点的球面,来降低离群点和噪声的影响。具体方法如下。
首先计算高维空间中所有样本点到各自类中心的距离:
(15)
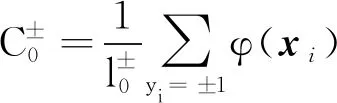
根据文献[24]中对离群值的定义,找出可能的离群点和噪声,这些可能的离群点和噪声满足以下条件:
d≥Q3+1.5Q,
(16)
Q=Q3-Q1,
(17)
其中,Q1为d0的第1位四分位数,Q3为d0的第3位四分位数。
去掉满足式(16)和式(17)的离群点和噪声,重新计算类中心和距离:
(18)
d±=‖φ(x)-C±‖ ,
(19)
此时得到的类中心是基于大多数样本点的。
然后计算隶属度为
(20)
其中,r±=max(d±)为样本点到类中心距离的最大值,表示正负类的半径。
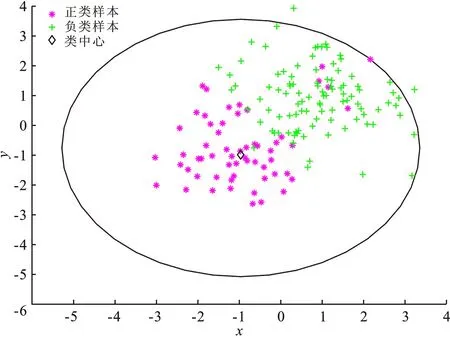
为了体现更新类中心和类半径对去除离群点和噪声的作用,随机生成一组数量为160的人工数据。首先找到正类样本点的类中心和类半径,得到包含所有样本点的球面,再对类中心和类半径进行更新,得到包含大部分样本点的球面,结果如图1所示。图1(a)中的类半径是基于所有样本点的,可以看出,受离群点的影响,初始的类半径很大,这可能导致计算得到的隶属度不准确。图1(b)中,通过计算样本点到原始类中心的距离识别出离群点,得到更新后基于大多数样本点的类半径和类中心,使得计算得到的模糊值更准确。
(a) IFSVM
2.1.2 非隶属度函数
衡量样本点的某个邻域内异类样本点与邻域内所有样本点关系的非隶属度函数,很大程度上依赖于邻域半径的选取。对于样本点稀疏的情况,若半径选取不当,就会造成非隶属度不准确。而核k近邻方法不会受到样本点分布稀疏的影响,能够保证非隶属度的准确性。因此,采用核k近邻的方法来计算样本点的非隶属度函数。具体做法如下:
对于样本点xi,先找到其在核空间中的k近邻{xi1,xi2,…,xik},核空间中样本点之间的距离计算公式为
(21)
计算非隶属度函数:
ν(xi)=(1-μ(xi))ρ(xi) ,
(22)

采用核k近邻方法计算样本点的非隶属度,可以避免样本点分布稀疏,且非隶属度函数邻域因子选取不恰当时,造成样本点非隶属度的不准确。在图1所示的人工数据上,分别找出正类样本中的边界样本点A,噪声B以及正常样本点C的邻域与k近邻,具体见图2。

(a) IFSVM
根据隶属度与非隶属度函数,得到如下直觉模糊集:
T={(x1,y1,μ1,ν1),…,(xm,ym,μm,νm)} ,
(23)
其中,μi,vi分别表示样本点xi的隶属度与非隶属度。定义其得分函数如下:
(24)
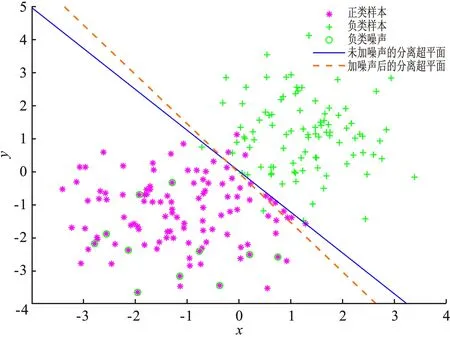
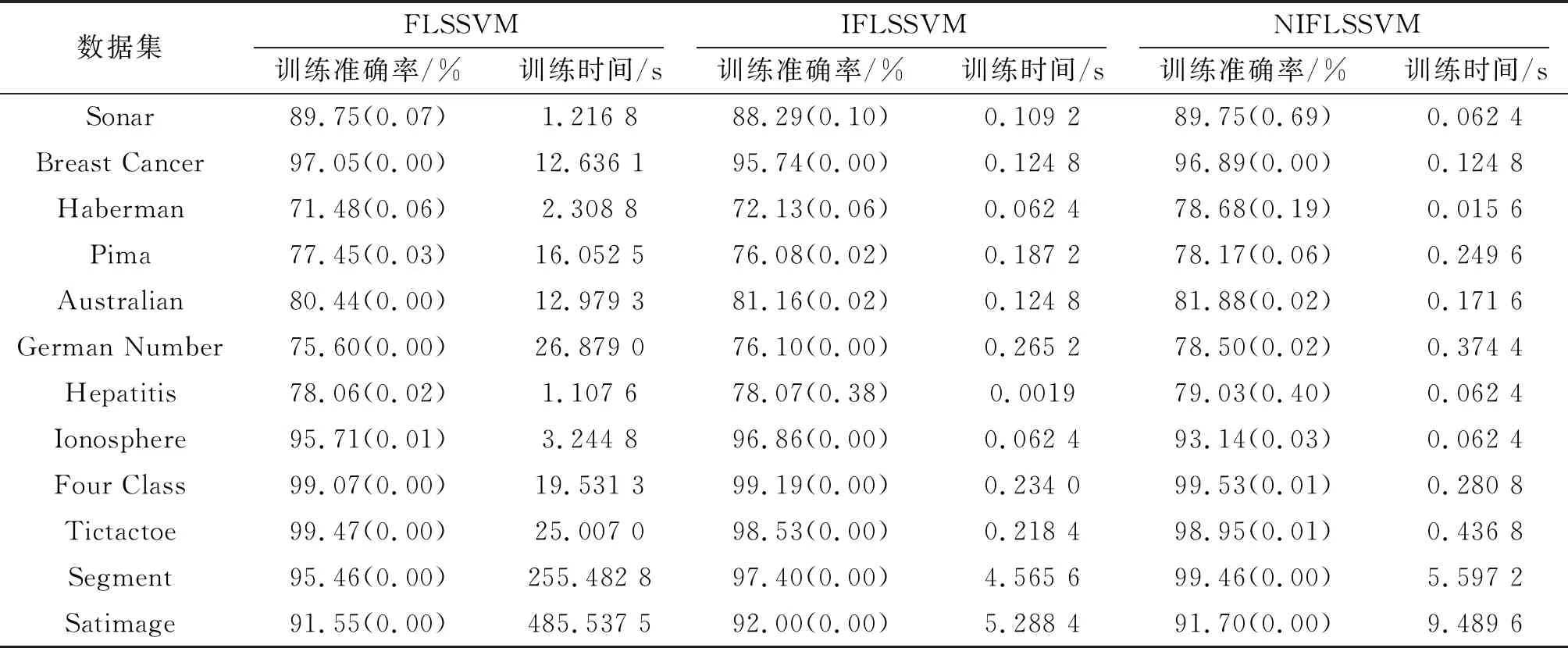
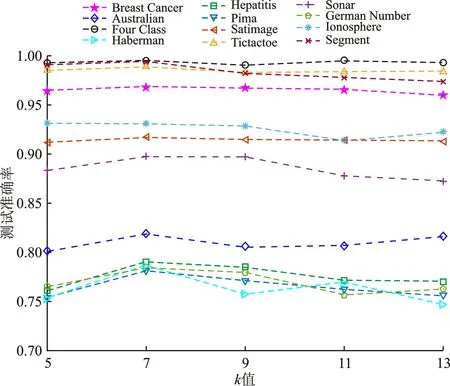
式(24)中将隶属度小于非隶属度(μi LSSVM模型易受离群点和噪声的影响,结合模糊支持向量机的思想,通过给离群点和噪声赋予更小的模糊值,可以减少离群点和噪声对模型的影响。因此,笔者将提出的模糊值用于改进LSSVM模型,得到新的直觉模糊最小二乘支持向量机(NIFLSSVM),其模型被表示为 (25) 其中,si为样本点xi的模糊值。 通过求解KKT条件可以得到如下线性方程组: (26) (27) 综上所述,把训练过程总结到算法1。 算法1NIFLSSVM算法。 输入:训练样本S={(x1,y1),…,(xm,ym)},yi={+1,-1},罚参数C,核参数δ及近邻数k。 输出:w。 ② 根据式(16)剔除样本点中的离群点,重新计算样本点的类中心C±和距离d±。 ③ 利用式(20)计算样本点的隶属度μ(xi)。 ④ 找出样本点的k个近邻里异类样本点的数量,利用式(22)计算样本点的非隶属度v(xi)。 ⑤ 根据μ(xi)与v(xi),利用式(24)计算样本点最终的模糊值s(xi)。 ⑥ 如式(25)所示,训练NIFLSSVM模型得到w。 笔者提出的NIFLSSVM算法在计算隶属度时,为了避免离群点的影响,采用了更新类中心和类半径的方法,相比已有的隶属度计算方法,用文中算法计算的隶属度更准确;计算非隶属度时,采用核k近邻的方法,可以自适应地选取半径计算非隶属度值,相比已有的非隶属度函数的计算方法,文中算法计算得到的非隶属度充分利用样本点分布特征,防止样本点被误判为噪声或离群点,得到的非隶属度值更合理。在计算模糊值时,采用得分函数结合样本点的隶属度与非隶属度给出最终的模糊值,充分利用样本点信息,提高了分类模型的准确性。进而将新的直觉模糊值与LSSVM模型相结合,得到了比FSVM模型训练速度更快的NIFLSSVM算法。 为了验证笔者提出算法的有效性,选取了1组人工数据和12个真实数据集进行实验。实验环境为Windows 7系统,8 GB内存,Intel(R)Core(TM)i7 4790 CPU的电脑,编程环境为Matlab R2018b。 为了直观地检验算法有效性,在人工数据集上进行实验。随机生成300个人工数据,选取200个数据进行训练,其余数据用作测试集。对训练集中的正类样本点采用标签反转的方式随机添加10%的噪声,得到带有噪声的人工数据集。将文献[23]中提出的直觉模糊数用于改进LSSVM模型,得到IFLSSVM算法,与笔者提出的NIFLSSVM算法进行对比。先在原始的人工数据集上进行训练,得到未加噪声的分离超平面,再在带有噪声的数据集上进行训练,得到新的分离超平面,分别比较两种算法的性能。两种算法在训练集上的分类结果见图3。可以看出,添加10%的噪声后,IFLSSVM的分离超平面的偏移较大,而NIFLSSVM的分离超平面几乎保持不变,说明NIFLSSVM可以有效减少离群点和噪声对分离超平面的影响。此外,IFLSSVM和NIFLSSVM在未添加噪声的测试集上的准确率均为98%,在添加噪声的测试集上的准确率分别为97.5%和98%。NIFLSSVM的测试准确率更高,可以更好地识别出噪声和离群点。 (a) IFLSSVM 使用UCI数据集来评估NIFLSSVM的性能。从UCI数据库选取12个数据集,相关数据集的详细信息见表1。对于所有的数据集,随机选取80%的样本作为训练集,剩余20%用于测试。所有的实验数据均进行归一化处理。实验分为两部分,节3.2.1中将文中算法与现有的鲁棒性算法进行对比,通过添加不同比值的噪声来对比模型的鲁棒性;节3.2.2中,将笔者提出的直觉模糊数与现有的模糊值进行对比,通过给LSSVM模型设置不同的模糊值来比较不同模糊值的优劣。 表1 数据集基本信息 在所有实验中,采用高斯核函数K(x1,x2)=exp(-σ‖x1-x2‖2),选取核参数σ∈{2-5,2-4,…,24,25},惩罚参数C∈{10-5,10-4,…,104,105}。同时采用五折交叉验证和网格参数寻优选取最优参数,所有实验在同一条件下重复10次求平均值统计结果。 3.2.1 与鲁棒性算法对比 为了验证笔者提出算法的鲁棒性,将NIFLSSVM与LSSVM、WLSSVM[10]、RLSSVC[12]、SRLSSVM[13]算法进行比较。对于RLSSVC,其正则化参数λ1、λ2的取值范围为{10-6,10-5,…,10-1,100}。在SRLSSVM中,设置平滑参数为p=104,停止标准ε=10-2,λ∈{10-1,100,…,104,105},核参数σ∈{2-8,2-7,…,23,24}。对于NIFLSSVM,参数k的取值范围为k∈{5,7,9,11,13}。 实验分为两部分:第1部分在真实数据集上对比5种算法的测试准确率,具体结果见表2;第2部分,为了进一步分析算法的鲁棒性,在数据集上分别添加5%、10%、15%、20%的噪声进行实验,计算上述5种算法在测试集上的准确率,实验结果见图4。 表2 在真实数据集上的实验结果对比 % 从表2可以看出,在大部分数据集上,WLSSVM、SRLSSVM、RLSSVC及NIFLSSVM算法的分类结果要优于LSSVM。同时相比于WLSSVM、SRLSSVM和RLSSVC,NIFLSSVM算法在大部分数据集上分类性能更好。就平均精度而言,NIFLSSVM要优于其余算法。实验结果表明,笔者提出的NIFLSSVM算法,通过给离群点和噪声赋予低的模糊值,可以有效减少离群值和噪声的影响,进而提高分类准确率。 由图4可以看出,随着噪声所占比值的增大,所有算法的性能均有所下降。SRLSSVM算法在大部分数据集上,随着噪声占比的增大,准确率变化不大,说明该算法更稳定,但其在数据集上整体的分类效果不佳。RLSSVC和WLSSVM算法随着噪声比值增加,准确率下降的趋势明显。在Sonar数据集上,RLSSVC的分类结果比LSSVM、WLSSVM及SRLSSVM更好,与NIFLSSVM相差不大。而NIFLSSVM在Tictactoe及Satimage两个数据集上分类性能一般,在其余数据集上测试准确率则要优于其余算法。实验表明,NIFLSSVM在添加了不同比值噪声的数据集上表现良好,可以有效减少离群点和噪声的影响。 图4 真实数据集上添加不同比值噪声的实验结果对比 3.2.2 与模糊支持向量机算法对比 将笔者所提模糊值与已有的模糊值进行比较。将文献[23]中提出的直觉模糊数结合LSSVM模型,得到IFLSSVM算法。将文献[17]中提出的模糊函数用于LSSVM模型,得到FLSSVM算法。在如表1所述的数据集上进行实验,验证算法的有效性。分别对比FLSSVM,IFLSSVM与NIFLSSVM的测试准确率与训练时间,实验结果见表3。 表3 与模糊支持向量机算法对比的实验结果 从表3可以看到,NIFLSSVM算法的分类结果要优于FLSSVM和IFLSSVM算法,而IFLSSVM在大部分数据集上的分类效果要优于FLSSVM。这是因为直觉模糊数既考虑了样本点对其所在类的隶属度,又考虑了样本点的非隶属度,得到的模糊值更为准确。而笔者提出的直觉模糊数,可以得到更为准确的隶属度与非隶属度,进而可以更加准确地识别出离群点和噪声。就训练时间而言,FLSSVM训练时间更长,这是因为FLSSVM需要提前训练一次LSSVM。而相比于IFLSSVM,NIFLSSVM训练时间稍长,这是因为NIFLSSVM需要更新类中心。 3.2.3k值对性能的影响 为了研究k值对NIFLSSVM算法分类性能的影响,在表1所述的12个真实数据集上进行了实验,研究当k取不同值时测试准确率的变化。设置k的取值范围为k∈{5,7,9,11,13},其余参数设置为由交叉验证得到的最优参数,实验结果见图5。 从图5可以看出,k值的变化对大部分数据集的测试准确率影响不大,主要原因是用k值计算样本点的非隶属度时,对正常样本点而言,非隶属度值很小或者为0,因此在最后计算模糊值时由隶属度起主导作用;对于噪声点,计算出的非隶属度大于隶属度,模糊值会被赋为0。由于非隶属度对样本点模糊值的影响较小,因此k值对最终的测试准确率影响较小。但是k值对于Haberman数据集的影响较大,这可能是数据集的数据分布导致的。此外还可以看出,大部分数据集在k=7时,测试准确率较高。 图5 测试准确率随k值变化结果图 笔者提出了一种新的直觉模糊最小二乘支持向量机(NIFLSSVM),充分利用样本点的隶属度与非隶属度信息为其分配直觉模糊数,通过对离群点和噪声分配低的模糊值来降低其对分类模型的影响,提高模型的鲁棒性。在人工数据集和UCI数据集上的实验表明,NIFLSSVM相比于其他鲁棒性算法有更好的性能,与不同的模糊值相比,笔者提出的直觉模糊数表现更好。但是在计算直觉模糊数时,耗时较长,需要改进。2.2 新的直觉模糊最小二乘支持向量机
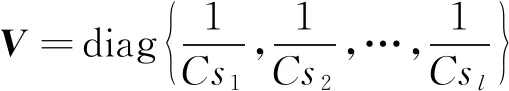
3 实验结果分析
3.1 人工数据集
3.2 UCI数据集


4 结束语
