一种多核极化码的缩短核矩阵构造方法
2022-12-01胡利港许丽卿谭晓青吕善翔
胡利港,许丽卿,谭晓青,刘 凌,吕善翔
(1.暨南大学 网络空间安全学院,广东 广州 510632;2.深圳大学 计算机与软件学院,广东 深圳 518060)
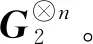
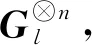
尽管上述穿孔方法能得到更加灵活长度的极化码,但维度较大时,穿孔过多会导致译码复杂度上升且影响核矩阵的指数。因此,笔者提出了一种基于列权重的缩短方法,并针对缩短后的核矩阵可能会出现部分距离超出对应上界的情况,提出了一种基于汉明距离的消除算法。首先,通过选取大指数的因子矩阵进行多核构造;然后根据部分距离的特性对得到的极化矩阵进行缩短操作。该方法构造的5阶核矩阵译码方法为多核极化码提供了更加灵活的码长。实验结果表明,该方法能以较低的复杂度得到任意维度的核矩阵,且得到的一些合数维核矩阵的指数高于由克罗内克乘积方法得到的指数。该方法与文献[15]中的工作相比,能够解决核矩阵最后一行全为1的情况;与同类型的缩短方法[13-14]相比,得到的核矩阵有着较大的指数。
1 极化矩阵与部分距离
在极化码中,拥有极化现象的生成矩阵称为极化矩阵,但不是所有的矩阵都有极化现象。给定一个l维的矩阵Gl,判断其是极化矩阵的充要条件是:Gl是非奇异矩阵且经过任意列变换不成上三角[16]。
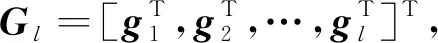
Di=dH(gi,〈gi+1,…,gl〉),i=1,2,…,l-1 ,
(1)
Dl=dH(gl,0) ,
(2)
其中,Di表示部分距离序列中的第i个元素,〈gi+1,…,gl〉表示括号中向量经过线性运算得到的所有向量的集合,0表示全零向量,函数dH表示汉明距离,D(Gl)表示部分距离序列。Gl的指数[17]定义如下:
(3)
(4)
在核矩阵的构造过程中,部分距离不能超过其上界[17]。设部分距离为Di,有Di≤dmax[l,l-i+1],其中dmax[l,k],1≤k≤l,表示长度为l,维度为k的二进制线性码最大的最小汉明距离。
克罗内克积多核构造就是利用不同维度矩阵或者同维度的不同矩阵通过克罗内克乘积运算进行核矩阵的构造。设vij(1≤j≤n)表示矩阵V的第i行和第j列的元素。V⊗U如下所示:
(5)
其中,V和U表示克罗内克积多核构造的因子矩阵。
2 极化码的核矩阵构造
2.1 极化码的编码
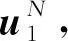
(6)
其中,GN表示生成矩阵。多核极化码的生成矩阵由因子矩阵及克罗内克乘积的顺序所决定,编码过程在tanner图上执行,如图1所示。tanner图有s个阶段,表示构造GN=Gn1⊗Gn2⊗…⊗Gns需要核矩阵的数量,每个阶段由N/nk个框组成,每个框都是描述核矩阵Gnk的nk×nk块。图1中P1称为连接编码位和阶段1的排列,P2称为连接阶段1和2的排列,LLR(vij)表示i阶段的第j个比特的似然比(Log-likelihood Ratio,LLR)的值。
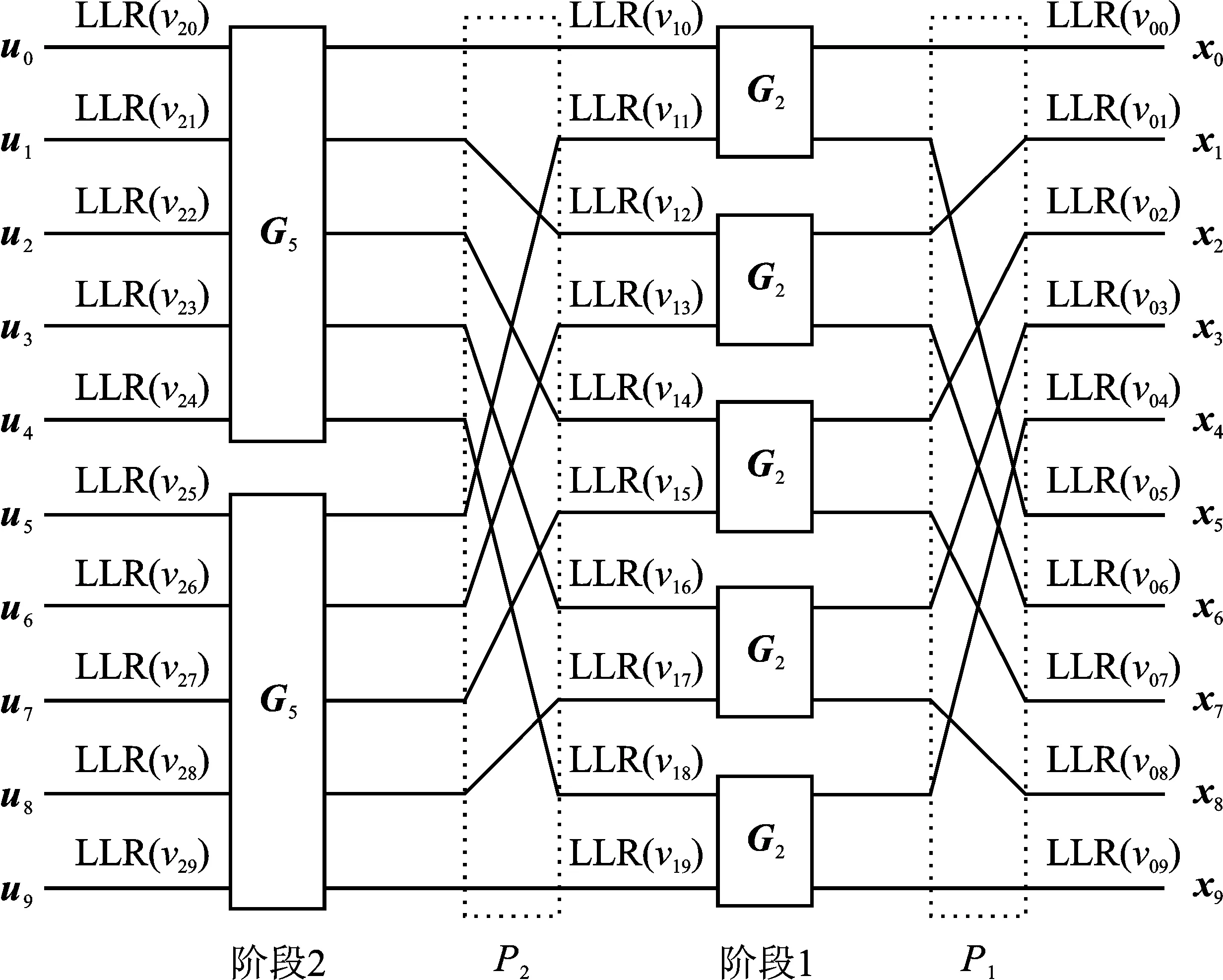
图1 多核极化码的tanner图
2.2 因子矩阵的选择
在多核极化码中,因子矩阵的选择直接关系到生成矩阵的性能。A和B表示极化矩阵,通过克罗内克乘积运算得到指数
(7)
从式(7)中能够得出
min (E(A),E(B))≤E(A⊗B)≤max (E(A),E(B)) 。
(8)
式(8)表明,因子矩阵A和B的指数越大,A⊗B的指数越大。
例2分别使用矩阵G2,G12和G3,G8构造24维矩阵。由文献[6]知E(G2)=0.5,E(G3)=0.420 620,E(G8)=0.5,E(G12)=0.492 100,因此有
2.3 基于列权重的缩短方法
基于列权重的缩短方法首先计算出矩阵中每一列1的权重,然后寻找除最后一列以外1的权重最低的一列。由于最后一行的部分距离较大,删除最后一行一列会对矩阵的指数产生较大影响,故将这种情况排除。若1的权重最少的一列惟一,设为第i列,则删除第i行第i列;若1的权重最少的一列不惟一,设靠前的一列为第j列,则删除第j行第j列。基于列权重的缩短方法流程图如图2所示。
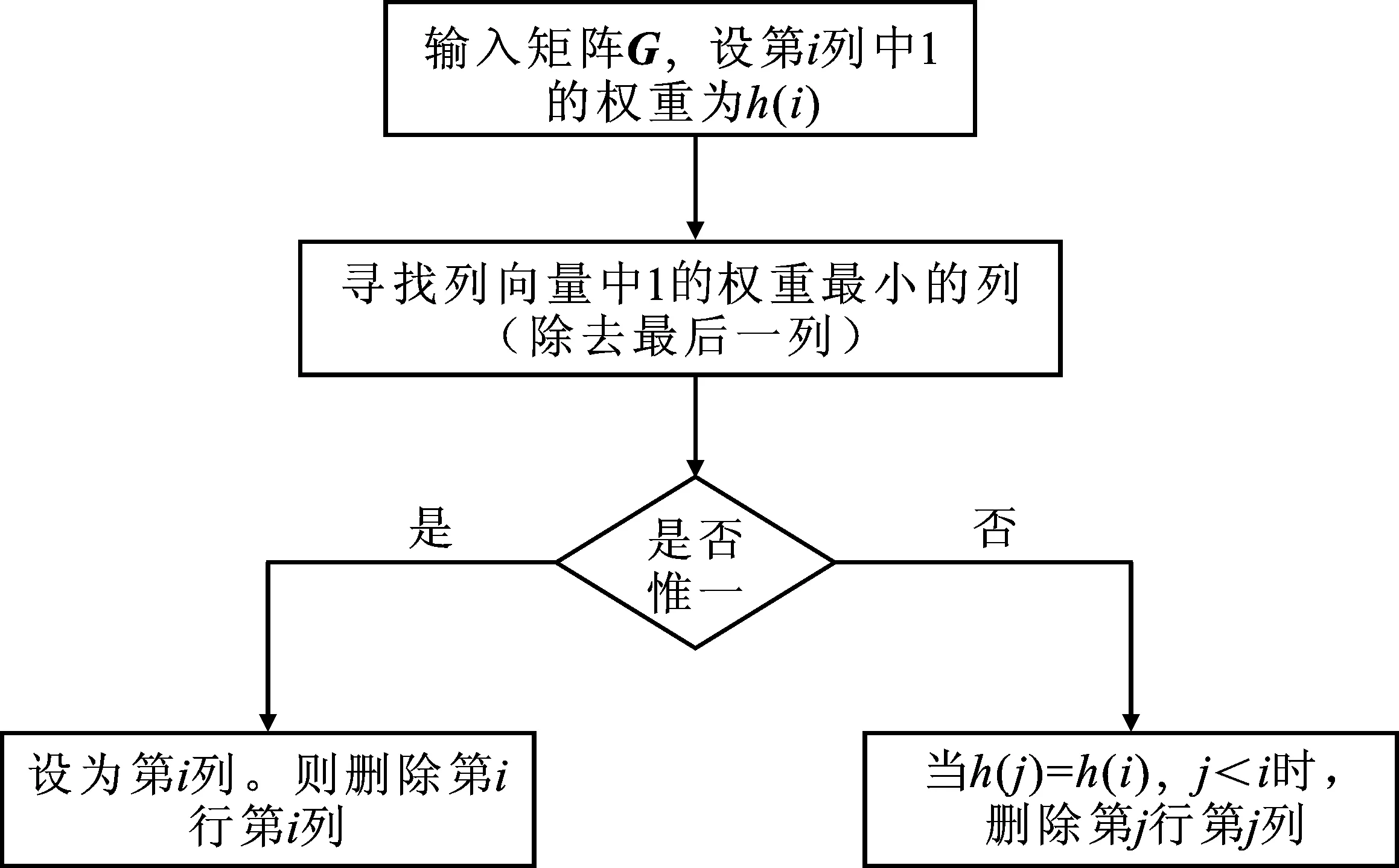
图2 基于列权重的缩短方法流程图
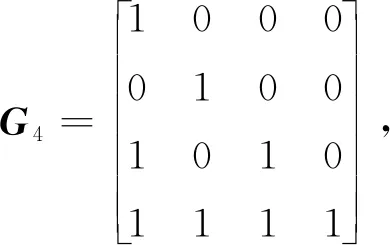
在构造核矩阵的过程中,以文献[6]中的矩阵作为因子矩阵,通过克罗内克乘积运算得到的矩阵仍然是下三角矩阵。故对极化矩阵Gl,有1≤Hmin≤2和h(l-1)≤2。其中Hmin=mini∈[1,l-1]h(i),表示1的权重最少的一列,h(i)表示第i列中1的权重。
当Hmin=h(j)=1时,设极化矩阵Gl的部分距离序列D(Gl)={D1,D2,…,Dl}。极化矩阵Gl删除第i行和第i列得到的矩阵设为G′l-1,部分距离序列为D(G′l-1)={D′1,…,D′l-1}。则有
D′k=Dk+1,j≤k≤l-1 ,
(9)
D′k≥Dk, 1≤k≤j-1 。
(10)
因为Gl是下三角矩阵,故对角线元素全为1。若Hmin=h(j)=1,则在第j列中,除了第j行的元素均为0。根据图2的方法,删除第j行和第j列。由式(1)知,删除第j行不影响其后所有行的部分距离。故可得出式(9)。当k≤j时,因为码字C′=〈g′k,…,g′l-1〉的汉明距离是通过缩短C=〈gk,…,gl〉得来的,所以有D′k≥dmin(C′)≥dmin(C)=Dk,故可得出式(10)。
当Hmin=1时,由式(9)和式(10)可知,缩短后的矩阵的部分距离序列至少不比缩短前差。当Hmin=2的时候,该方法会影响到矩阵的部分距离序列,但由于列向量中的1较少,产生的影响较小。
例3对矩阵
(11)
根据基于列权重的缩短方法删除第4行第4列,得到的部分距离序列为D(G′7)={1,2,2,2,3,3,7},指数为E(G′7)≈0.456 825。通过穷举法得到7阶最大指数矩阵的部分距离序列为D(G7)={1,2,2,2,4,4,4},指数为E(G7)≈0.457 981。当需要的矩阵维度较大时,穷举不切合实际。
2.4 基于汉明距离的消除算法
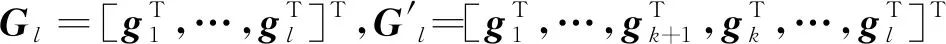
E(G′l)≥E(Gl) ,
(12)
D′k+1>D′k。
(13)
构造核矩阵的过程中,基于汉明距离的消除算法能够解决部分距离超出其对应上界的问题。该算法通过将行向量中的1替换成0,以改变行向量的部分距离,得到满足部分距离上界的行向量。具体描述如下:


③ ifD1≤S1,D2≤S2,…,Dk≤Sk
④ returnD(Gl1⊗Gl2)=(D1,D2,…,Dk)
⑤ else
⑥ 若Di>Si(1≤i≤k)
⑦ 将gi中的1替换成0,得到g′i,wt(g′i)表示g′i的汉明距离,D′i表示g′i的部分距离,且满足wt(g′i)=Si
⑧ returnD′(Gl1⊗Gl2)=(D1,D2,…,D′i,…,Dk)
⑨ end if
根据式(1)能够得出Di≤wt(gi),故D′i≤wt(g′i)=Si。步骤⑦中将1替换成0,存在以下两种方法:
方法1 从左往右将1替换成0,从而减少行向量gi中1的权重,得到g′i,且满足wt(g′i)=Si。
方法2 从右往左将1替换成0(不改变矩阵下三角的性质),从而减少行向量gi中1的权重得到g′i,且满足wt(g′i)=Si。
不改变矩阵下三角的性质即不将矩阵对角线上的1替换成0,目的是为了保证矩阵的极化性质。由标准型矩阵的特征以及式(1)可知,方法2对第i行之前的行向量部分距离影响较大,得到的指数低于方法1。故步骤⑦采用方法1。
例4选取通过缩短方法得到的19维矩阵的前6行:

(14)

2.5 多核极化码的译码
在实际应用中,编码方法需要一种有效的译码方法。类似文献[20],多核极化码的译码[5]是通过SC译码算法在tanner图上进行的,其译码算法由核矩阵的译码规则所确定。
传统极化码的G2核描述[1]如下:

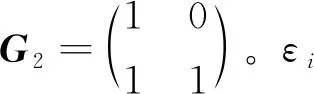
(15)
多核极化码的性能取决于因子矩阵及其乘积顺序,在不考虑乘积顺序的情况下,因子矩阵本身就显得尤为重要。不同维度核矩阵的译码方法使多核极化码的码长有了更多的选择。图1中G5核的描述如下:
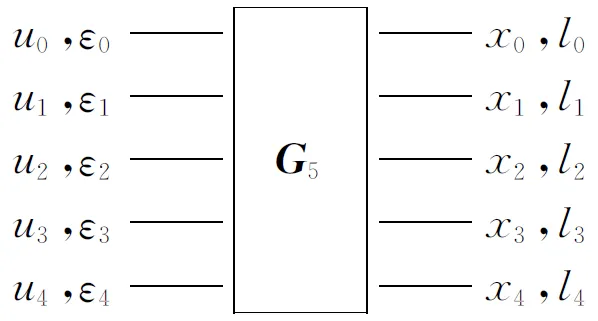
根据式(6),有(u0,u1,u2,u3,u4)×G5=(x0,x1,x2,x3,x4),其中
(16)
因此,硬决策的更新规则为x0=u0⊕u1⊕u2⊕u3⊕u4,x1=u1,x2=u2⊕u4,x3=u3⊕u4,x4=u4。由此可得u0=x0⊕x1⊕x2⊕x3⊕x4,u1=x1=u0⊕x0⊕x2⊕x3⊕x4,u2=x2⊕x4=u0⊕u1⊕x0⊕x3,u3=x3⊕x4=u0⊕u1⊕u2⊕x0⊕x4,u4=x4=u2⊕x2=u3⊕x3=u0⊕u1⊕u2⊕u3⊕x0。最后得到消息更新方程式:
ε0=l0⊙l1⊙l2⊙l3⊙l4,
(17)
ε1=l1+(-1)u0(l0⊙l2⊙l3⊙l4) ,
(18)
ε2=l2⊙l4+(-1)u0⊕u1(l0⊙l3) ,
(19)
ε3=l3⊙l4+(-1)u0⊕u1⊕u2(l0⊙l4) ,
(20)
ε4=l4+(-1)u2l2+(-1)u3l3+(-1)u0⊕u1⊕u2⊕u3l0。
(21)
根据G2核的消息更新方程式有LLR(v10)=LLR(v00)⊙LLR(v05),LLR(v12)=LLR(v01)⊙LLR(v06),LLR(v14)=LLR(v02)⊙LLR(v07),LLR(v16)=LLR(v03)⊙LLR(v08),LLR(v18)=LLR(v04)⊙LLR(v09)。根据上式计算出LLR(v20),然后对u0进行硬判决,最后完成对u0的译码。以此类推下去能够相继译出u1至u9。
3 数值分析
表1比较了由克罗内克乘积运算和基于列权重的缩短方法得到的极化矩阵的指数。其中第2列的“/”表示无法通过克罗内克乘积运算得到的素数维矩阵的指数,第3列中的“/”表示未使用基于列权重的缩短方法,指数通过克罗内克乘积运算得出。从表1中可以看出,克罗内克乘积运算不能得到的素数维矩阵,基于列权重的缩短方法能够通过缩短高出一维的矩阵得出,例如17,19,23,29,31维矩阵。一些能够通过克罗内克乘积运算得到的合数维矩阵,同样能够通过该方法得出,且有更大的指数,例如21,25,27维矩阵。其中19维矩阵的D6经过行变换之后超出了上界3,通过基于汉明距离的消除算法得出最后的指数。
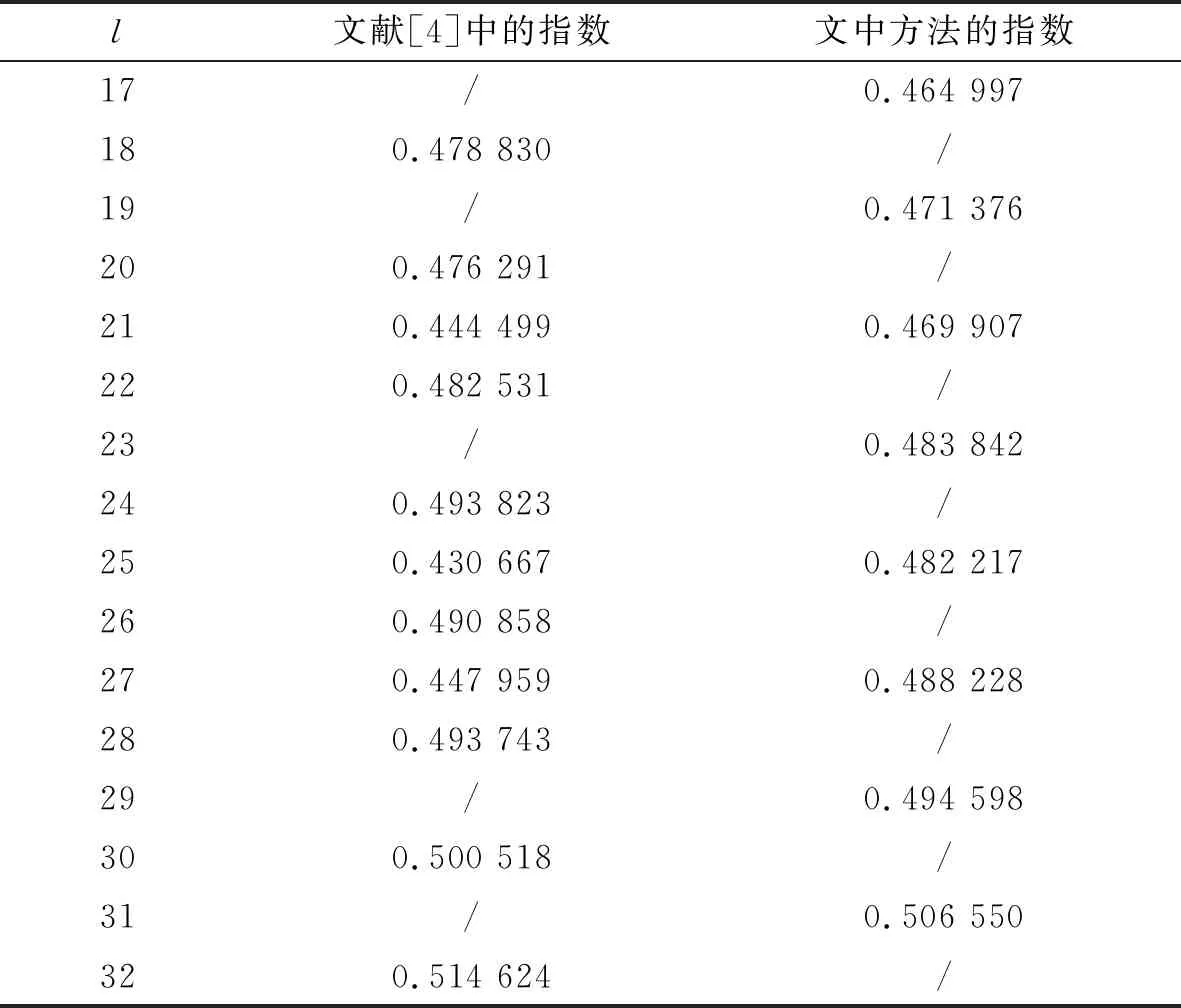
表1 文献[4]与文中方法的指数比较
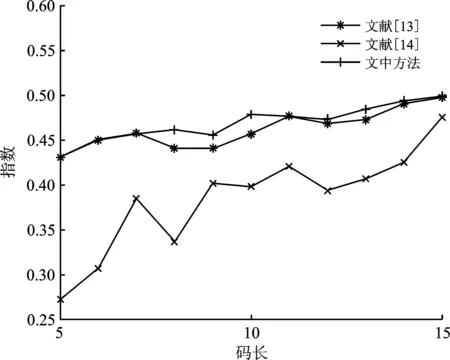
为了体现基于列权重的缩短方法的优越性,图3比较了通过不同方法缩短多核极化矩阵得到素数维极化矩阵(5 图3 不同缩短方法对多核极化矩阵的指数比较 图4 不同缩短方法对穷举极化矩阵的指数比较 与传统的穿刺/缩短方法相比,多核极化码的译码长度较小,译码复杂度更低。通过SC或SCL译码算法的穿刺/缩短的极化码是在其母码的tanner图上执行的,即译码复杂度取决于母码长度。基于列权重的缩短方法与多核极化码有着相同的译码复杂度,即译码复杂度低于传统的穿刺/缩短极化码。传统的穿刺/缩短极化码的译码复杂度为N′lbN′,其中N′表示母码的长度。因此当N=19和N′=32时,需要计算160个LLRs。基于列权重的缩短方法在G20=G2⊗G2⊗G5的基础上缩短,仅需计算60个LLRs。 笔者提出了一种多核极化码的缩短核矩阵构造方法。该方法在多核构造的基础上,充分考虑了缩短核矩阵过程中1的权重对核矩阵指数的影响,得到的核矩阵有着较大指数,打破了多核极化码不能构造素数维矩阵的局限性。同时,针对构造核矩阵的过程中出现的部分距离超出其对应的上界的情况,笔者还提出了一种基于汉明距离的消除算法。该方法构造的5阶核矩阵译码方法使多核极化码有着更灵活的码长。实验表明,基于列权重的缩短方法能够弥补克罗内克积多核构造无法构造素数维核矩阵的缺陷,并且与同类型的缩短方法相比,该方法在指数和译码复杂度方面具有优势。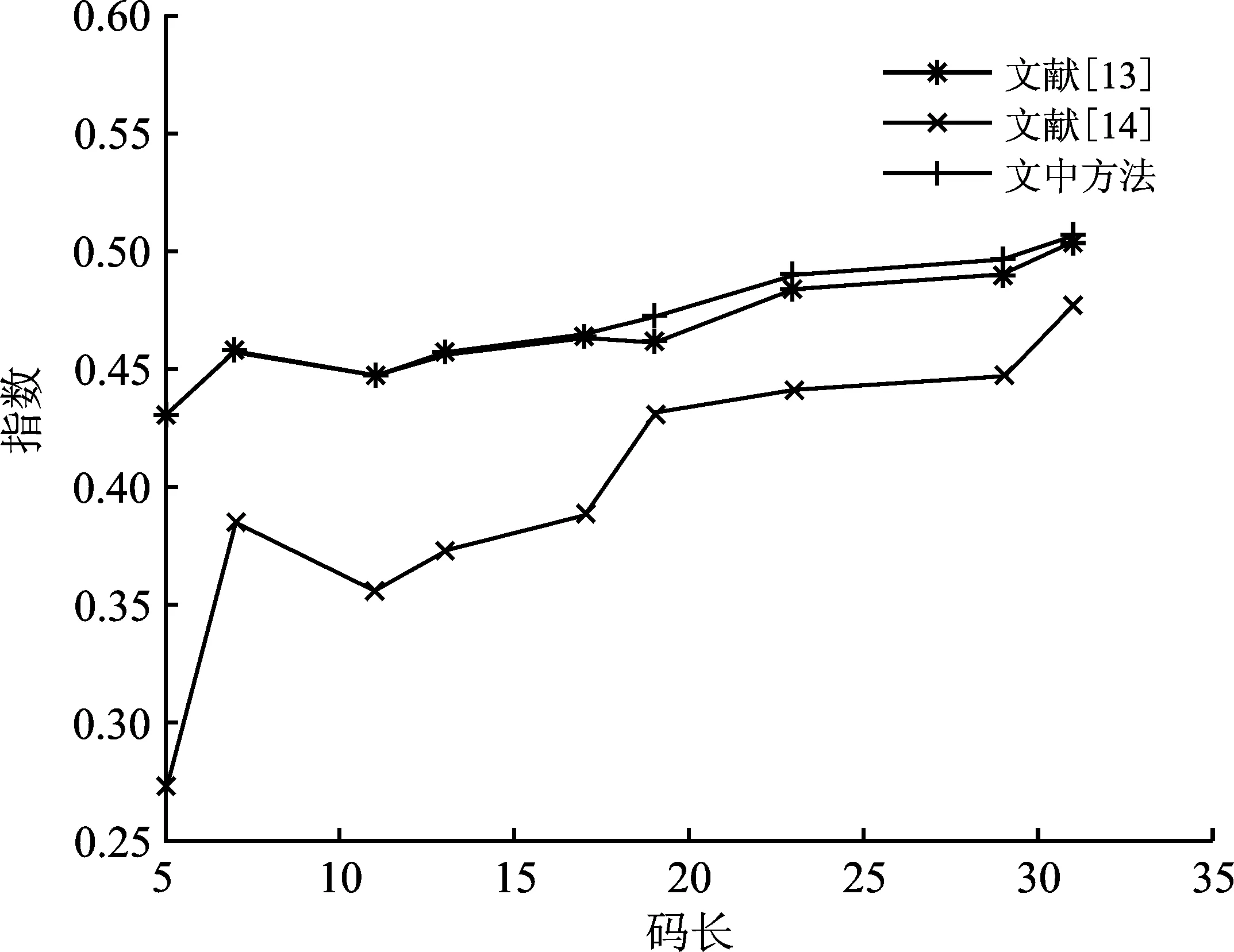
4 结束语
