多传感器协同地面目标跟踪的调度方法

张昀普，单甘霖，付 强

(陆军工程大学石家庄校区 电子与光学工程系，河北 石家庄 050000)

目前，各级军事侦察系统中均配备有数量众多、种类各异、功能互补的侦察传感器，用来完成各类侦察探测任务。相比传统的单传感器独立工作，依托信息融合技术的传感器管理方法可以将多传感器真正整合成一个整体，从而大幅提升系统的侦察效能[1-2]。

传感器调度作为传感器管理研究的一个重要分支，其侧重于对传感器系统在每一时刻的动作(如开关机状态、波束指向和机动方向等)进行控制，可根据具体的任务需要建立相应的优化准则，并实时地选择传感器的调度方案以获取所需优化指标的最优度量值，从而获取最佳的任务收益[3]。目前，针对传感器调度的研究主要集中在面向目标跟踪任务的调度方法中，所用的优化指标包括信息增益、跟踪精度和辐射代价等。文献[4]使用Rényi信息增益作为优化指标，基于该指标提出了多传感器协同多目标跟踪的调度方法，实现了对多目标的持续跟踪。文献[5]针对主/被动传感器系统协同目标跟踪问题，将传感器的跟踪精度和辐射代价的加权和达到最小作为调度依据，提出了相应的传感器调度方法。文献[6]考虑了移动传感器系统，并将传感器调度拓展到长期调度上来，以目标的长期跟踪精度为优化指标提出了相应的调度方法。

然而，现有文献大多是针对空中目标进行研究，此类目标的运动方式不受约束，通常用匀速或转弯模型即可表征，传感器的跟踪准则也较为简单[7]。但在实际中，也存在对地面目标的跟踪需求，此类目标相比空中目标的运动方式更为复杂，传感器跟踪时所需考虑的因素也更多。地面目标探测传感器(如地面动目标指示系统)多采用脉冲多普勒系统，为了消除地杂波对目标指示的影响，地面目标探测传感器通常会设置一个最小可检测速度(Minimum Detectable Velocity，MDV)，与传感器间的径向速度小于该速度的目标将进入传感器的多普勒盲区，从而造成量测丢失[8]。在实际侦察任务中，敌方地面目标通常速度较慢，且会采用动-停-动的方式运动，这会造成目标极易落入多普勒盲区，从而成功躲避传感器跟踪。此外，由于传感器的检测概率必然小于1，即使目标在多普勒盲区外，传感器也并非总能获取其量测[9]。因此，在面向地面目标跟踪进行传感器调度时，需要对丢失量测值的不同情况予以考虑，以保证调度方法的合理性。

为解决上述问题，笔者面向地面目标跟踪任务，以多普勒体制的传感器系统为研究对象，对相应的传感器调度方法进行研究，从而实现在多普勒盲区存在的情况下动态地选择合适的传感器以获取最优的跟踪精度。首先建立了传感器调度的基本模型；然后基于地面目标的动-停-动运动方式建立了目标跟踪模型，依据速度大小将目标运动分为低速和高速两个状态，给出了状态概率的计算方法，并引入了变结构交互式多模型(Variable Structure Interacting Multiple Models，VSIMM)方法对目标状态进行估计；最后以目标的长期跟踪精度最佳为优化目标，建立了长期调度的优化模型，并给出了跟踪精度的量化方法。

1 基本模型

1.1 调度动作

k时刻传感器系统的调度动作即为传感器的工作方案，用N×1维矩阵Uk=[u1，k，….，un，k….，uN，k]T表示。其中，un，k(1≤n≤N)表示传感器n的开关机状态，其取值为1或0，当un，k=1时，表示调度该传感器开机跟踪目标；当un，k=0时，表示该传感器静默。笔者不考虑多个传感器之间的量测值融合，故规定在每时刻仅调度一部传感器跟踪同一目标，因此调度动作的约束条件可表示为

(1)

在时间步长为H的时域[k，k+H-1]上，对应的长期调度动作可表示为Uk：k+H-1=[Uk，Uk+1，…，Uk+H-1]。

1.2 目标状态转移方程

(2)

在k时刻，当目标处于停止模型时，其速度(不考虑噪声)必为0，因此，可假设目标在k-1至k时刻做匀减速直线运动，且在k时刻静止，因此，目标的运动状态可表示为(以X方向为例)：

(3)

其中，τ为传感器的采样间隔。基于上式，停止模型的状态转移矩阵可写为

(4)

1.3 传感器量测方程

目标量测值Zk包含斜距离、方位角和径向速度信息，可通过量测方程表示[11]，即

(5)

(6)

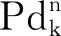
2 目标跟踪模型

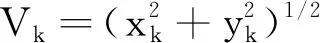
为了解决上述问题，根据目标速度的大小设置两类速度状态，分别为：

(1) 高速状态ΩF，该状态下目标的速度大于停止极限速度Vlimit，其无法在一个采样间隔内停止。

(2) 低速状态ΩS，该状态下目标的速度小于等于Vlimit。

2.1 状态概率

由1.2节可知，使用4种模型，分别为匀速直线模型(i=1)、匀加速直线模型(i=2)、匀速转弯模型(i=3)和停止模型(i=4)，则高速状态下的状态转移矩阵为

(7)

相应地，低速状态下的状态转移矩阵为

(8)

值得注意的是，由于过程噪声的存在，当目标处于停止模型时，其速度并不一定为0，因此文中设定一个较小的边缘速度V0，当Vk≤V0时，即可视为目标已经停止。

目标在k-1时刻处于不同速度状态的概率与目标的历史量测值Z1：k-1有关，即

(9)

(10)

Vlimit=adτ+V0=adτ+(6)1/2στ，

(11)

其中，ad为目标在一个采样间隔内的最大减速度。可以看出，速度大于Vlimit的目标不能在一个采样间隔内停止。

进一步，结合式(9)，可得目标在k-1时刻处于低速和高速状态的概率：

(12)

2.2 VSIMM方法

由于停止模型仅在无量测时才会被考虑，传统的IMM方法无法适用于这种模型集时变的场景。因此，使用VSIMM方法对时变模型集下的目标状态进行估计，VSIMM方法能够根据每时刻系统状态对模型集进行更新，可弥补IMM方法下模型集固定的问题[9]。当被调度的传感器无法获取目标量测时，停止模型会被加入到模型集中，此时停止模型在前一刻的模型概率被设置为0，而当获取量测值后，停止模型则会被删除，其他模型的概率将被重新归一化。

在每一时刻确定模型集后，即可按照传统的IMM框架对目标的状态进行估计。当量测值存在时，可结合粒子滤波方法进行估计[9]，当无量值时，仅根据模型递推对预测状态进行估计。在状态估计的过程中，需要确定模型的似然函数和状态转移概率，下面将结合地面目标的运动特性介绍二者的计算方法。

2.2.1 似然函数

在传统的IMM方法中，默认传感器一定能获取量测值，在k时刻模型i的似然函数可表示为[14]

(13)

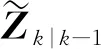
(14)

其中，δ(Zk)为指示函数，当Zk=0时(即无量测时)，δ(Zk)=1，否则，δ(Zk)=0。

2.2.2 状态转移概率

由2.1节可知，目标运动分为低速状态和高速状态，不同状态具有不同的状态转移矩阵，因此应综合考虑两类状态来计算模型间的状态转移概率。结合全概率公式，在k时刻由模型i转移到模型j的概率可表示为

(15)

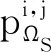
(16)

3 传感器调度优化模型

传感器调度需要选取合适的优化指标，并基于优化指标对未来收益进行预测，从而制定出收益最佳的传感器调度方案。由于以未来多步收益总和最优为决策依据的长期调度在性能上优于以一步收益最优为决策依据的短期调度[6]，结合目标跟踪任务实际，笔者选择以目标的长期跟踪精度作为优化指标。后验克拉美罗下限(Posterior Cramér-Rao Lower Bound，PCRLB)能根据当前先验信息预测未来时刻目标状态估计误差的理论下界，常用于衡量非线性系统的跟踪精度[15]，因此选择PCRLB的迹量化目标跟踪精度。PCRLB为Fisher信息矩阵的逆矩阵，以符号Ψ(Xk)表示Fisher信息阵，则Ψ(Xk)满足以下递推关系[15]：

(17)

其中，

(18)

当决策步长为H时，结合传感器调度动作的约束条件式(1)，可建立长期调度的目标函数如下：

(19)

4 仿真实验

4.1 仿真参数设置

我方部署8部传感器(记为S1-S8)跟踪敌方1个地面目标，目标的初始位置为(0 m，0 m)，初始速度为(30 m/s，30 m/s) 。仿真时间为100 s，采样间隔为1 s，目标在1～15 s以-4°/s的角速度做匀速转弯运动，在16～30 s以4°/s的角速度做匀速转弯运动，在31～50 s以-2 m/s2的加速度做匀加速直线运动，在51～55 s停止，在56～70 s以2 m/s2的加速度做匀加速直线运动，在71～82 s以-2 m/s2的加速度做匀加速直线运动，在83～89 s停止，在90～100 s以3 m/s2的加速度做匀加速直线运动运动，目标运动轨迹及传感器位置示意图如图1所示。各传感器的MDV均为8 m/s，其他参数见表1，低速和高速下的状态转移矩阵为

图1 目标运动轨迹及各传感器位置

表1 传感器参数

其他参数：过程噪声在X和Y方向的标准差σ=2.5 m，最大减速度为ad=4 m/s2，折扣因子α=0.9，蒙特卡罗次数为200次。

在仿真中，引入均方根误差(Root Mean Square Error，RMSE)和均方根误差的时间平均值(Root Time Average Mean Square Error，RTAMSE)作为衡量跟踪精度优劣的评价指标。

4.2 仿真结果分析

决策步长H决定了决策时对未来状态的预测步数，从而直接影响到调度结果。为确定H的大小，在H=1～5下进行了仿真，图2给出了每时刻不同H下目标位置和速度的RMSE，表2给出了对应的RTAMSE值。可以看出，在H=1～3时，跟踪精度随着H的增加而提高，即传感器调度的收益提高，这说明在一定程度上增大H，可以提升传感器调度的效果；而当H>3时，精度反而随着H的提高开始下降，这是由于在决策时，H的值过大导致对系统未来状态的预测准确度降低，致使得到的传感器调度动作并非最优动作，从而影响了实际的跟踪效果。因此，在调度中，决策步长H的取值并非越大越好，依据图2和表2的结果，在接下来的仿真中取H=3。

(a) 位置RMSE

表2 不同H下目标位置和速度的RTAMSE

为了更好地说明笔者所提调度方法(长期调度，H=3)的调度性能，采用3种调度方法进行对比，分别为：

方法1：全程使用检测概率和精度均最高的传感器6跟踪；

方法2：最近邻调度方法[5]，每时刻调度距目标最近的传感器；

方法3：随机调度方法[16]，每时刻随机调度传感器。

图3给出了不同调度方法下目标位置和速度的RMSE，表3给出了目标位置和速度的RTAMSE值，图4给出了文中方法对应的传感器调度动作。可以看出，文中方法通过对系统和目标状态进行预测，并根据预测信息进行最优决策得到最佳的传感器调度动作，可在最大程度上避免多普勒盲区的出现，能够保持对目标较好的跟踪效果，获得了几种方法中最佳的跟踪精度。方法1虽然全程使用跟踪精度最佳的传感器6，但实际跟踪精度并不佳，这是由于跟踪精度与目标和传感器的相对位置有关，该方法未结合目标实际状态进行传感器调度，致使效果不佳。方法2在每时刻调度距目标最近的传感器，在理论上可获得较佳的跟踪精度，但其与方法3一样，没有通过解算目标函数求出最佳工作方案，致使二者的调度效果均不如文中方法。综上，仿真结果说明通过解算基于目标长期跟踪精度最佳的目标函数，从而求取最佳传感器调度动作的方法是合理且可行的，验证了笔者所建模型和所提方法的有效性。

(a) 位置RMSE

表3 不同方法下目标位置和速度的RTAMSE

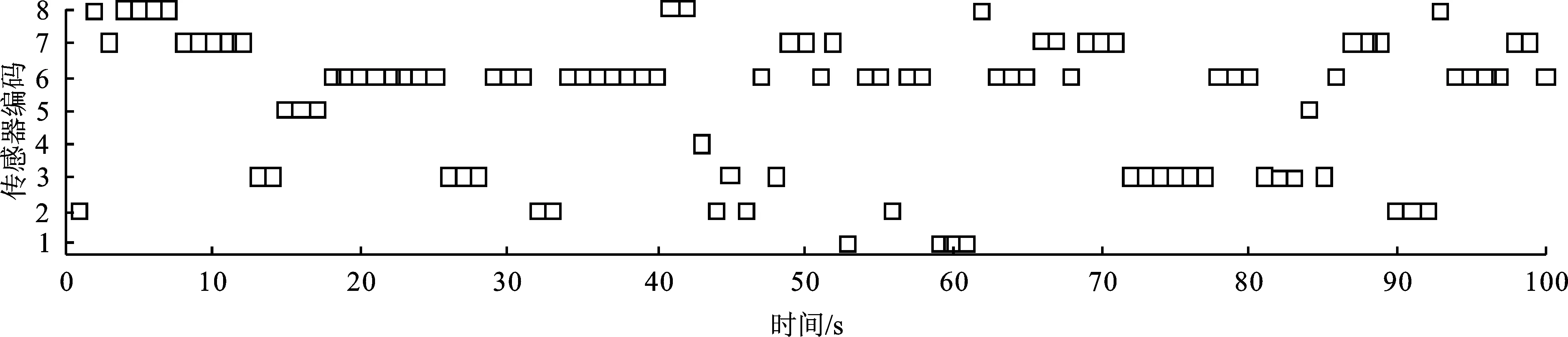
图4 文中方法所得调度动作

5 结束语

面向多普勒盲区存在下的地面目标跟踪任务，为实现对目标的高精度持续跟踪，笔者提出了一种传感器调度方法。建立了调度的基本模型，对调度动作、目标状态转移和盲区存在下的传感器量测进行了数学描述；在目标跟踪模型中考虑了地面目标动-停-动的机动特点，将目标运动状态分为低速和高速，并引入VSIMM方法对目标状态进行估计，结合目标量测值丢失的两种原因和目标运动模型给出了似然函数和状态转移概率的计算方法；引入PCRLB量化目标跟踪精度，并以此为优化指标建立了长期调度的目标函数；仿真实验证明了模型和调度方法的有效性。在下一步的研究中，应在传感器调度方法中考虑密集杂波、崎岖地形和电磁干扰等因素，使方法更贴合实际需求。