GCN-GRU：一种无线传感器网络故障检测模型

陈俊杰，邓洪高，马 谋，蒋俊正，2

(1.桂林电子科技大学 信息与通信学院，广西壮族自治区 桂林 541004；2.桂林电子科技大学 卫星导航定位与位置服务国家地方联合工程研究中心，广西壮族自治区 桂林 541004)

随着微处理器等技术的不断发展和进步，使用无线传感器网络(Wireless Sensor Network，WSN)实时监测环境信息逐渐成为一种广受欢迎的新方法。目前，无线传感器网络作为信息处理系统的数据采集端口，已经被广泛用于军事防御、灾害预警和智能农业等各个领域[1-2]。由于传感器通常部署在较为恶劣的环境，因此传感器故障是普遍存在的。然而，如果系统不能及时检测出故障传感器节点，就会丢失或误报信息，导致决策失误、仪器损坏等不可预估的后果。因此对无线传感器网络节点进行故障检测是至关重要的[3-]。传感器故障可以分为硬故障和软故障[5]，硬故障是指传感器节点的硬件设施出现故障，无法获取信息或和其他节点通讯；软故障是指传感器虽然可以继续工作，但节点获取的信息或传输的信息不准确。由于软故障的传感器处于不稳定的工作状态，故障检测的难度也相对较大，所以，笔者主要针对软故障进行故障检测。

无线传感器网络中传感器所采集的数据具有空间相关性和时间相关性的特点[6-7]。空间相关性指地理位置相邻的传感器具有相近的测量值；时间相关性指同一传感器在相邻时刻具有相近的测量值。无线传感器网络故障检测算法通常利用这些特点，对传感器网络中出现的故障进行检测。如CHEN等[5]提出的分布式故障检测(Distributed Fault Detection，DFD)算法，该算法通过网络中相邻节点之间的互相测试以确定节点的初始状态，再依据节点以及相邻节点的初始状态信息进一步判断节点是否故障。分布式故障检测算法具有较高的检测精度和较低的误报率，但故障检测精度在邻居节点个数较少的情况下会迅速下降；为此，文献[8]提出了新的分布式故障检测算法(New Distributed Fault Detection，NDFD)，该算法定义了新的检测标准，有效地提高了在邻居节点个数较少情况下的故障检测精度。基于分簇的算法[9]将无线传感器网络中的节点划分为簇，再利用时间或空间相关性对簇中的节点进行故障检测，基于中值策略的算法[10]将节点测量值与其所有邻居节点测量值的中位数进行比较，若差值超过所设定的阈值，则认为该节点故障。由于中值能很好地反映实际的数值分布，因此基于中值策略的算法通常具有较高的检测精确率。随着神经网络的发展，利用神经网络进行故障检测也逐渐受到学者的关注，如文献[11]中提出的基于后向传播神经网络的故障检测方法，利用神经网络强大的非线性拟合能力进行故障检测，该方法能针对不同的传感器网络进行学习，具有较强的适应能力。

在上述算法中，基于后向传播神经网络的故障检测方法仅通过神经网络非线性拟合能力进行故障检测，并未考虑传感器网络中的时间特征和空间特征；基于中值策略的算法仅考虑了无线传感器网络节点的空间特征，并未考虑传感器网络中的时间特征；分布式故障检测等算法虽然同时考虑到了空间特征和时间特征，但仅使用了相邻时刻与当前时刻的差值信息，未能充分利用时间演变特性。基于上述问题，笔者提出了一种融合了图卷积网络[12](Graph Convolutional Network，GCN)和门控循环单元[13](Gate Recurrent Unit，GRU)的故障检测模型GCN-GRU，通过该模型对无线传感器网络中的故障传感器进行检测。为了充分利用传感器网络的空间特征和时间特征，首先通过图模型来刻画无线传感器网络的空间相关性，从而利用GCN提取传感器网络的空间特征；其次，将图卷积网络所提取的空间特征与无线传感器网络采集数据相融合后送入GRU，在GRU中通过对上一时刻的信息进行适当的舍取，从而提取出无线传感器网络的时间特征；最后，由全连接层将时空特征拟合为故障检测结果。仿真结果表明，与DFD算法、NDFD算法和GRU算法相比，GCN-GRU模型取得了更高的故障检测率和更低的虚警率，表明该模型能更有效地利用WSN的空间特征和时间特征。

1 传感器网络图建模

节点vi与vj之间最短路径的边数被定义为测地距离ρ(i，j)，若vi没有路径到达vj，则ρ(i，j)=∞。通过测地距离可以得到vi的k阶邻居定义B(i，k)≡{j|ρ(i，j)≤k}[16]，即与vi测地距离小于等于k的节点集合。传感器网络所采集数据在不同时刻具有一定的差异性，如图1(b)所示，因此传感器网络在T个连续时刻内采集的数据可以表示为X=[x1，x2，…，xT]，其中，xT=[x(v1)，x(v2)，…，x(vn)]T表示传感器网络各节点在t时刻采集数据的集合，即表示为t时刻的图信号。图1(b)中，xi，t表示序号为i的传感器节点在t时刻采集的数据。

(a) 传感器网络结构示意图

通过构造图模型，无线传感器网络故障检测问题可以描述为：在一定区域内部署了由n个传感器构成的传感器网络，该传感器网络在T个连续时刻内采集的数据为X，xt表示t时刻传感器网络所采集的元素，即待检测信号集合；[xt-T+1，xt-T+2，…，xt-1]表示传感器网络的历史信号集合。通过构建故障检测模型对X及传感器网络的图模型G进行分析，检测xt是否含有故障节点；若含有故障节点，则进一步定位出对应的故障传感器。

2 GCN-GRU模型

当完成图建模之后，使用GCN-GRU模型对无线传感器网络中的故障节点进行检测。GCN-GRU模型的结构示意图如图2所示。模型主要结构分为3个部分，分别是输入层、时空处理层和输出层。输入层接收传感器网络数据X及其图模型的邻接矩阵A，并将其作为时空处理层的输入。时空处理层由图卷积模块和GRU组成，首先图卷积模块接收来自输入层的数据，通过图卷积运算提取传感器网络数据的空间特征S∈RT×n×2，之后将S与X进行数据拼接后作为GRU的输入，利用GRU提取传感器网络数据的时空特征H并传输至全连接层，最后通过全连接层将时空特征H拟合为概率矩阵Y并将其传输至输出层，其中概率矩阵Y的元素表示对应节点的分类概率。输出层将Y转化为故障检测结果并输出。图2中输出层的阴影节点表示GCN-GRU模型检测出的故障节点。

图2 GCN-GRU模型结构示意图

2.1 图卷积模块

GCN模块接收传感器网络数据X及其图模型的邻接矩阵A，并通过图卷积操作提取其中的空间特征。图卷积被定义为滤波器gθ=diag(θ)与图信号x∈Rn在频域的乘积，如式(1)所示，

(1)

(2)

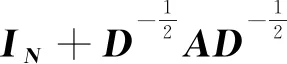
(3)

(4)

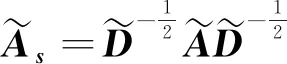
(a) k=0 (b) k=1 (c) k=2

2.2 门控循环单元

GRU接收由GCN模块提取的空间特征S，并将其与原始信号X拼接后作为输入，得到无线传感器网络的时空特征H：

H=tanh(fGRU([S，X])) ，

(5)

其中，tanh表示双曲正切激活函数；[S，X]∈RT×n×3表示将S与X拼接为新的三维数据；H为GCN-GRU模型所提取的时空特征。GRU的内部结构如图4所示，GRU通过上一个时刻的输出ht-1和当前时刻的输入xt获取重置门rt和更新门zt的状态：

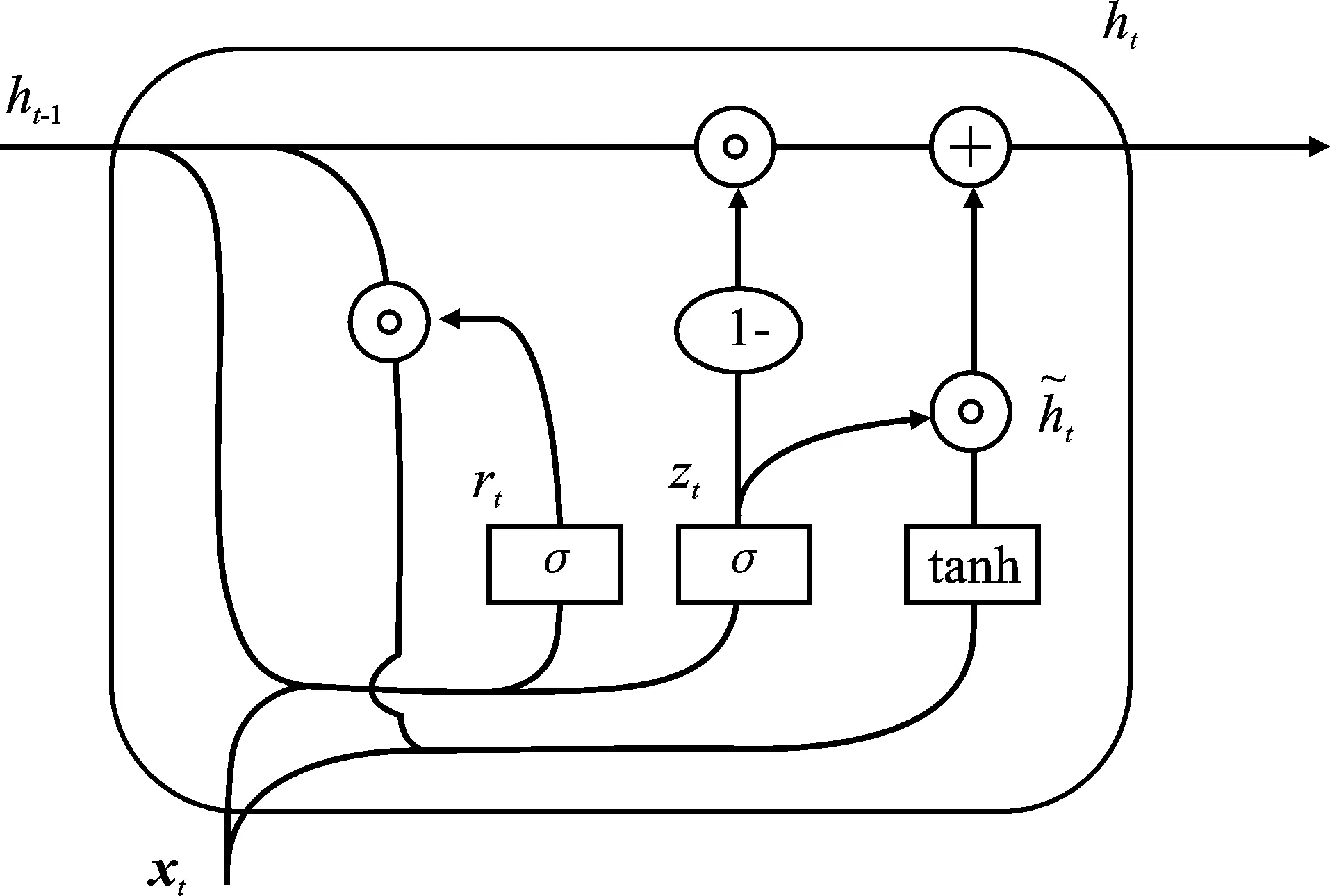
图4 GRU内部结构图

(6)

(7)

(8)

其中，更新门zt用于确定上一个时刻的输出ht-1对当前时刻输出ht的影响程度。

最后，将GRU所提取的时空特征H作为全连接层的输入，得到分类概率矩阵Y。GCN-GRU模型中全连接层的前向传播公式如下式所示：

Y=fFC(H)=σ(WFCH+b) ，

(9)

3 实验仿真结果及分析

3.1 实验数据集

第1个仿真实验所使用的数据是由美国国家气象局官方网站所公布的美国主要城市2003年的日平均气温数据集[16]。该数据记录了分布在美国各地的150个传感器365日获取的日平均气温，采样时间间隔为1天，气温范围为[-17.8 ℉，104.3 ℉]，℉表示华氏度。如图5(a)所示，这150个传感器组成了一个复杂的传感器网络。

(a) 无异常节点图信号

该数据集是一个无异常的数据集，仿真时在原始数据的基础上增加20 ℉以模拟传感器发生故障，20 ℉对该数据而言是非常小的变化，难以通过人工排查出异常数据。图5展示了某时刻无故障节点图信号与模拟传感器故障后的图信号的对比，其中节点颜色的深浅表示温度的低高，图5(b)中星形节点表示故障节点。

第2个仿真实验所采用的数据集由大气海洋联合研究所公布的全球500个传感器在1948年至2010年内4599个时刻采集的海平面气压[15]。数据集内海平面气压范围为[94.713 6 kPa，110.513 4 kPa]，采样时间间隔为5天。图6展示了该数据集传感器网络所构成的图模型。

图6 海平面气压数据集中的传感器网络

与第1个仿真实验采用的数据集类似，在仿真时将数据在原本的基础上增加3 kPa作为故障传感器测量的异常值。图7为某时刻无故障节点图信号与模拟传感器故障后的图信号的对比，与图5类似，节点颜色的深浅表示海平面气压的低高，图7(b)中星形节点表示故障节点。

(a) 无异常节点图信号

3.2 实验设置

数据集以6∶4的比例被随机划分为训练集和测试集，为了模拟现实中的故障情况，将训练集中出现故障传感器的时刻设置为总数的10%，测试集为5%，故障时刻的故障传感器数量为传感器总数的5%。对于当前时刻是否发生故障，需要利用其前3个连续时刻的无异常数据进行检测。详细参数设置如表1所示。

表1 实验具体参数

实验选择Python作为编程语言并使用Pytorch 1.6建立网络模型，利用RMSprop优化器对模型参数进行优化。RMSprop是一种基于梯度的神经网络损失函数优化算法，它在减小更新波动范围及加快收敛速度上有着明显的优势，在很多情况下都被认为是工作性能优秀的优化器。交叉熵损失函数经常被用于分类问题，因此被选择为训练过程中的损失函数，其定义如式(10)所示。

(10)

检测率PDR、故障检测率PFDR和虚警率PFAR是常用于评价传感器网络故障检测结果的指标[18]。检测率、故障检测率和虚警率可以通过真正例NTP、假正例NFP、真反例NTN和假反例NFN来表示。NTP是指模型分类为正例，实际上也是正例的个数；NFP是指模型分类为正例，实际上为负例的个数；NTN是指模型分类为负例，实际上也是负例的个数；NFN是指模型分类为负例，实际上是正例的个数。将故障视为正例，正常视为负例。由此，可以得到PDR、PFDR和PFAR的定义：

(11)

由定义可以看出，检测率是指模型将样本正确分类到对应类别的个数占总样本数的比例；故障检测率是指模型正确分类为正例的样本占所有正例样本的比例；虚警率是指模型错误分类的样本数占总样本数的比例。

3.2 仿真结果及分析

分别选取DFD算法[5]、NDFD[8]算法和GRU[13]作为对比算法，仿真结果如表2所示。由表2可以看出，笔者提出的GCN-GRU模型对比DFD算法、NDFD算法和GRU有着更高的检测率和故障检测率以及更低的虚警率，整体检测性能显著优于对比算法。GCN-GRU模型通过两层卷积层聚合了每个传感器节点的两阶邻居信息，充分地利用了无线传感器网络的空间相关性，因此GCN-GRU模型的性能明显优于仅使用时间特征的GRU模型；相较于DFD和NDFD算法，GCN-GRU模型通过GRU提取了传感器网络数据的时间特征，对时间样本数据的特征提取能力更强，因此本模型在检测故障传感器问题上有着更出色的表现。综合来看，GCN-GRU模型与对比算法相比有着更好的故障检测性能，体现了该模型在时空特征的提取和利用方面有着更好的表现，能够有效地处理无线传感器网络故障传感器检测问题。

表2 不同数据集下各算法的评价指标 %

4 结束语

笔者提出了一种新的传感器网络故障检测模型。首先通过GCN提取传感器网络的空间特征；再将所提取的空间特征与输入信号结合后作为GRU的输入，利用GRU提取其中的时空特征；最后将时空特征送入全连接层，将其拟合为故障检测结果。仿真结果表明，笔者提出的GCN-GRU模型优于DFD算法和NDFD算法，具有更好的故障检测性能。

后续工作将设计适用于更加复杂情况下的传感器网络故障检测模型。