陀螺随机误差补偿中一种改进混合降噪法

田 易，阎跃鹏，钟燕清，李继秀，孟 真

(1.中国科学院微电子研究所，北京 100029；2.中国科学院大学 集成电路学院，北京 100049)

微机电系统(Micro ElectroMechanical System，MEMS)陀螺是惯性导航系统中的核心器件之一，在姿态测量[1-2]领域有着广泛的应用。陀螺的测量精度直接影响姿态的解算精度，而随机误差是影响微机电系统陀螺测量精度的重要因素之一。目前关于陀螺随机误差的补偿主要包括基于多尺度小波变换[3-4]的方法、基于卡尔曼滤波(Kalman Filter，KF)[5]的方法、基于前向预测滤波(Forward Linear Prediction，FLP)的方法[6-8]等。基于经验模态分解(Empirical Mode Decomposition，EMD)的方法于1998年由HUANG等提出[9]，是一种新型的信号分解方法，适用于对非线性、非平稳信号的降噪处理[10]，已广泛应用于对微机电系统陀螺随机误差的消除[11-15]。但由于经验模态分解易产生模态混叠的问题[16]，因此集成经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法[17]、互补集成经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)方法[18]、自适应噪声的完整经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN)方法[19]被相继提出。但是EEMD和CEEMD方法都存在添加不同随机噪声导致分解本征模态函数数量不同的问题，而CEEMDAN通过附加自适应白噪声，不仅能减轻模态混叠现象，还可以精确重构原始信号，可有效提高微机电系统陀螺信号的测量精度[20-21]。

在常规CEEMDAN算法中，信号分解为一系列的本征模态函数(Intrinsic Mode Functions，IMFs)后，将低阶噪声本征模态函数去除且将第一阶本征模态函数用于混合本征模态函数滤波的阈值确定。然而载体运动状态突然改变而导致陀螺传感器数据发生阶跃变化时，低阶噪声IMFs中将混入高频信号，一方面直接去除噪声本征模态函数将引起数据高频信号丢失，另一方面将导致滤波阈值提升引起对混合本征模态函数过度滤波问题。因此笔者提出了一种改进的CEEMDAN-FLP混合滤波算法，对噪声本征模态函数和噪声信号混合本征模态函数分别采用软阈值(Soft Interval Thresholding，SIT)滤波和FLP进行噪声消除的改进算法，在降噪的同时实现对高频信号的最大保留，为惯性导航后处理提供高精度的陀螺测量数据。

1 CEEMDAN-FLP基本原理

1.1 CEEMDAN基本原理

CEEMDAN是基于EEMD的一种改进算法，可有效解决经验模态分解过程中的模态混叠问题，与EEMD方法相比，有效减少了迭代次数，增加了重构精度。CEEMDAN的解算步骤如下：

(1) 在原始信号中分别添加I组满足均值为0、标准差为β0的随机噪声，构成I组序列，其中第i组序列为x(n)+β0ωi(n)，ωi(n)为满足标准正态分布的随机白噪声。对添加噪声后的序列分别进行EMD分解，则第1阶IMF满足

(1)

(2) 残差满足

(2)

(3) 第2阶IMF满足

(3)

(4) 以此递推，第k阶残差满足

(4)

(5) 第k+1阶IMF满足

(5)

(6) 重复至(4)，直到rk满足终止调减，因此趋势项满足

(6)

最终经过CEEMDAN分解后，信号x(n)被分解为若干IMFs和一个趋势项，满足

(7)

1.2 FLP基本原理

FLP滤波是一种适用于陀螺噪声消除的滤波方法，其利用之前多个时刻的原始数据乘以对应的权重值来预测当前时刻的数据，作为滤波器的输出[7]，即

x(n)=WT(n)X(n-1) ，

(8)

其中，X(n-1)=[x(n-1)x(n-2) …x(n-N)]T，为x(n)之前的数据，N为FLP滤波阶数；W(n)为权重系数，满足

W(n+1)=W(n)+μ(n)e(n)X(n-1) ，

(9)

其中，e(n)为预测值与实测值的差值，μ(n)则为步长调整因子，用以控制自适应过程的收敛速度和失调参数。

1.3 软阈值滤波原理

(10)

计算第1个IMF的噪声方差σ1，通过中值估计法得到：

(11)

(12)

各阶IMF的噪声阈值与第1个噪声阈值的关系满足

(13)

根据文献[13]的结果，取H=0.5，β和ρ分别为0.719 和2.01。

2 改进CEEMDAN-FLP混合滤波算法

改进CEEMDAN-FLP混合滤波算法原理如图1所示。对陀螺数据进行CEEMDAN分解，得到一系列频率由高到低变化的窄带IMFs信号和一个趋势项。由于有用信号中多为低频信号，噪声信号中多为高频信号，因此，随着IMFs的阶数增加，IMFs中包含的噪声分量逐渐减小，信号分量逐渐增加。根据IMFs中包含噪声分量和信号分量的多少，可以将IMFs区分为噪声主导IMFs、信号噪声混合IMFs和信号主导IMFs，对不同类型的IMFs采取不同的处理方式，达到对信号滤波降噪的目的。

图1 改进CEEMDAN-FLP混合滤波算法框图

首先，采用连续均方误差分析(Consecutive Mean Square Errors，CMSE)来区分噪声IMFs与混合IMFs，该方法不需要任何外部参考信息[11]。在噪声IMFs和混合IMFs分类判别中，将连续的两个重构信号作比较，来判断这两个信号的相似程度。

(14)

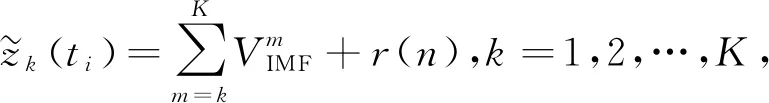
因此，CMSE值的大小反映了连续的两个重构信号的相似程度，也反映了各阶IMFs中的信号能量多少。随着IMFs阶数增加，CMSE的值呈先减小后增大的变化规律。CMSE值先减小，是由于低阶IMFs中几乎不含信号，而噪声分量随着阶数的增加而降低；CMSE后增大，是由于IMFs中信号分量的出现，并随阶数增长逐渐增加。因此，将CMSE取值最小时的IMFs阶数，作为噪声IMFs与混合IMFs的分界点M1，满足[11]

(15)

D(i)=dist[PDF(x(t))，PDF(IMFi(t))]， 1≤i≤n。

(16)

M2=arg max[D(i)]+1 。

(17)

将IMFs区分为噪声IMFs、混合IMFs和信号IMFs后，提出了一种改进CEEMDAN-FLP混合滤波算法。改进算法对CEEMDAN与FLP混合滤波进行了尝试，并采用新的滤波方式，对噪声IMFs进行软阈值滤波，避免常规算法将噪声IMFs直接剔除引起的高频信号丢失问题；对混合IMFs进行FLP滤波，避免由于阈值提升引起的过度滤波问题。最后，将经过软阈值滤波的噪声IMFs、经过FLP滤波的混合IMFs与信号IMFs和趋势项进行数据重构，得到最终的降噪信号。改进算法可在消除噪声的同时，更有效地保留信号中的高频分量。

3 仿真验证与分析

模拟载体运动状态突然改变的情况，在理想的阶跃信号上添加均值为0、均方差为2°/s，满足正态分布的随机噪声作为陀螺信号，对其进行CEEMDAN分解，并根据CMSE法和IMF与原始信号的2阶范数分析法分别确定IMFs分类，其噪声IMFs与混合IMFs的分界如图2所示。由于3阶IMFs的CMSE值最小，因此，噪声IMFs与混合IMFs的分界为M1=3。信号IMFs与混合IMFs的分界如图3所示，混合IMFs与信号IMFs的分界为M2=6。

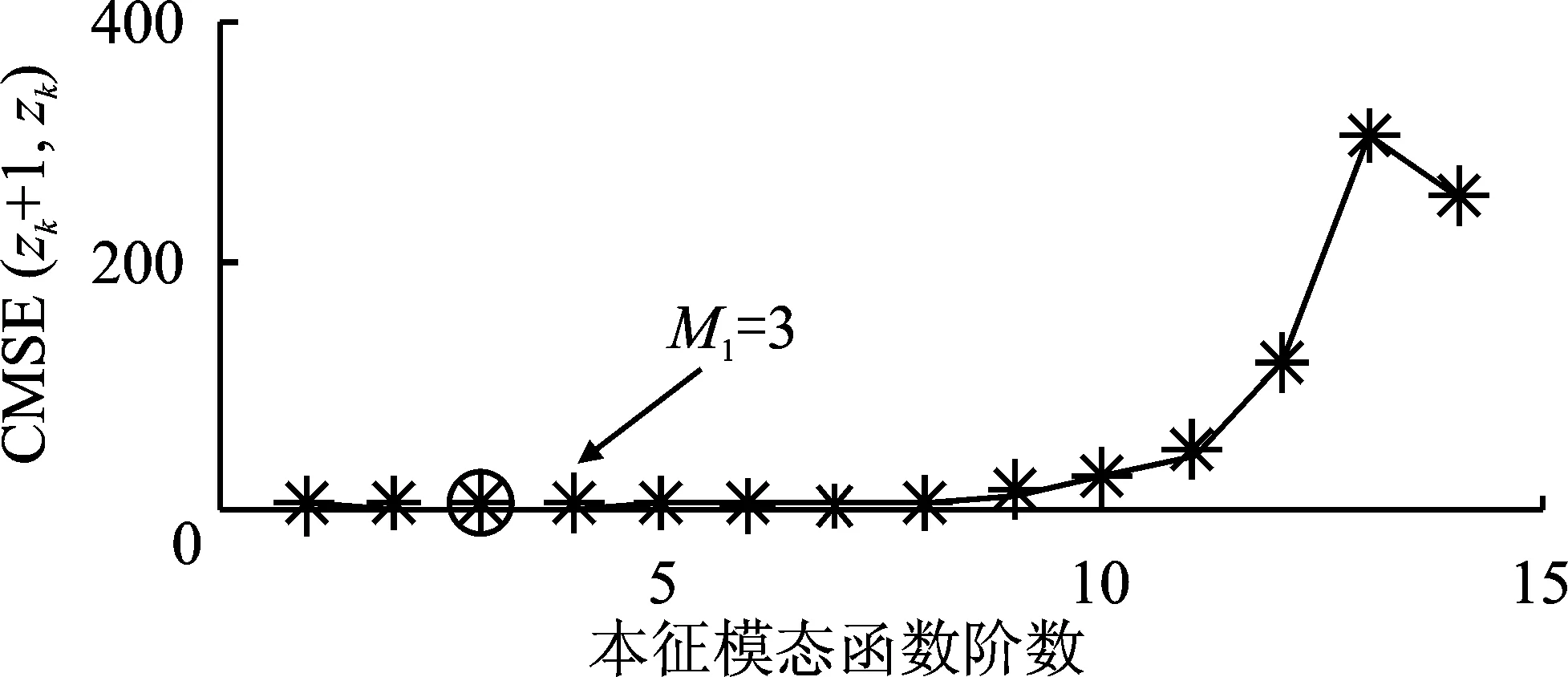
图2 噪声IMFs与混合IMFs的分界

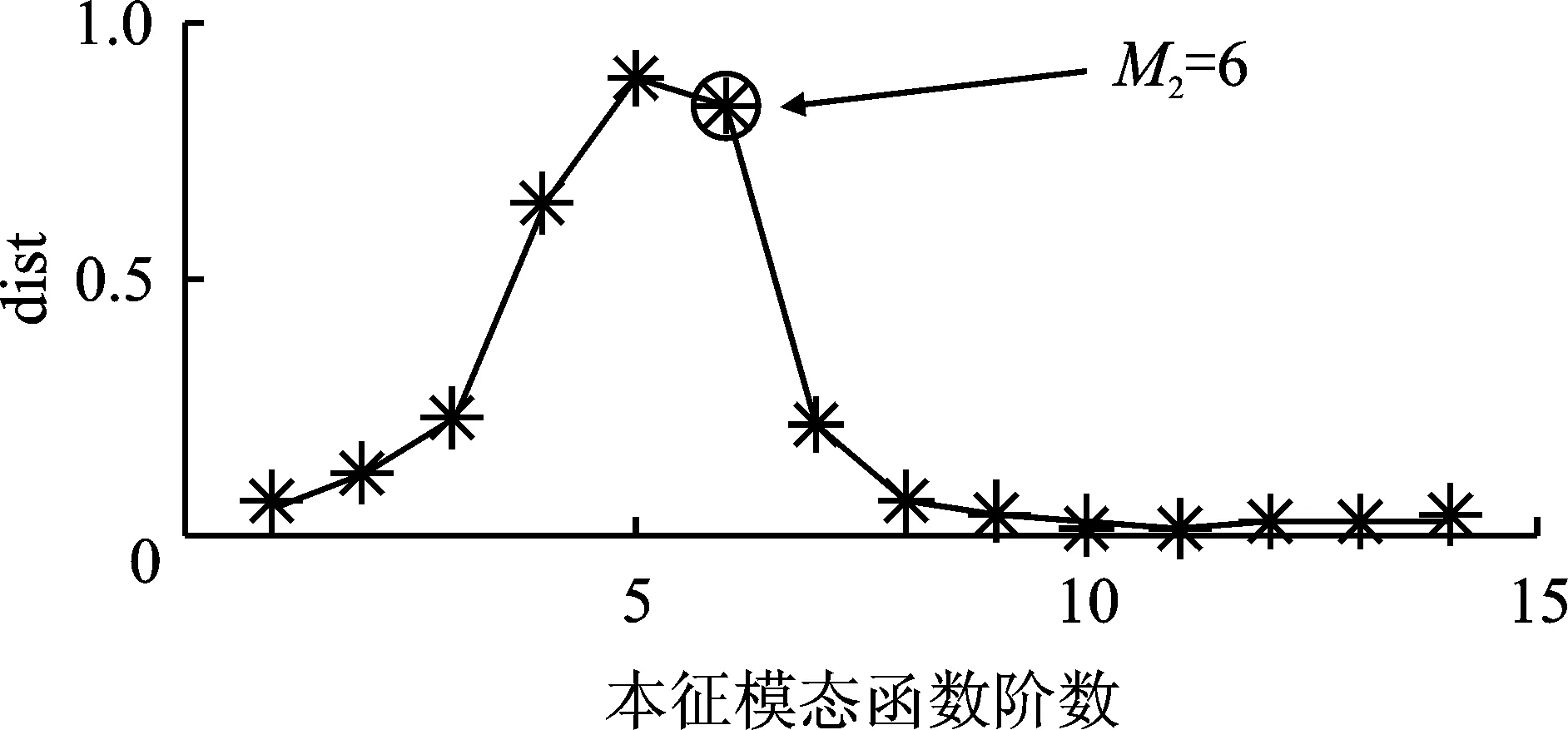
图3 信号IMFs与混合IMFs的分界

1～3阶IMFs被划分为噪声IMFs，4～6阶IMFs被划分为信号噪声混合IMFs，而7阶以上则为信号IMFs。对噪声IMFs采用软阈值滤波(以3阶IMF为例)，滤波结果及19 s处的细节放大图如图4所示。由图可见，噪声IMFs中明显包含着有用的高频信号信息，通过软阈值滤波，实现了对噪声的滤除，同时保留了有用的高频信号。对混合IMFs采用FLP滤波(以4阶IMF为例)，滤波结果及19 s处的细节放大图如图5所示。由图可见，混合IMFs中的有效信号得到了充分保留，噪声得到了明显抑制。

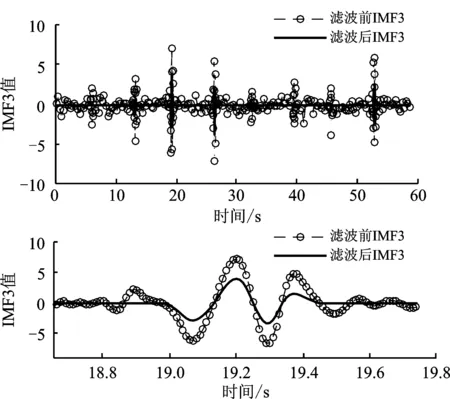
图4 噪声IMF3的软阈值滤波前后对比

图5 混合IMF4的FLP滤波前后对比

将滤波后的噪声IMFs和混合IMFs与信号IMFs进行数据重构，得到滤波降噪后的陀螺数据，将改进CEEMDAN-FLP滤波结果与原始数据、EMD滤波结果、CEEMDAN滤波结果及未改进CEEMDAN-FLP滤波结果进行仿真对比，结果及29 s和52 s处的细节放大图如图6所示。从图6中可以看到，改进算法在信号突变时，具有最优的动态跟踪能力，CEEMDAN-FLP算法次之，而传统的EMD数据延时最大，信号失真。

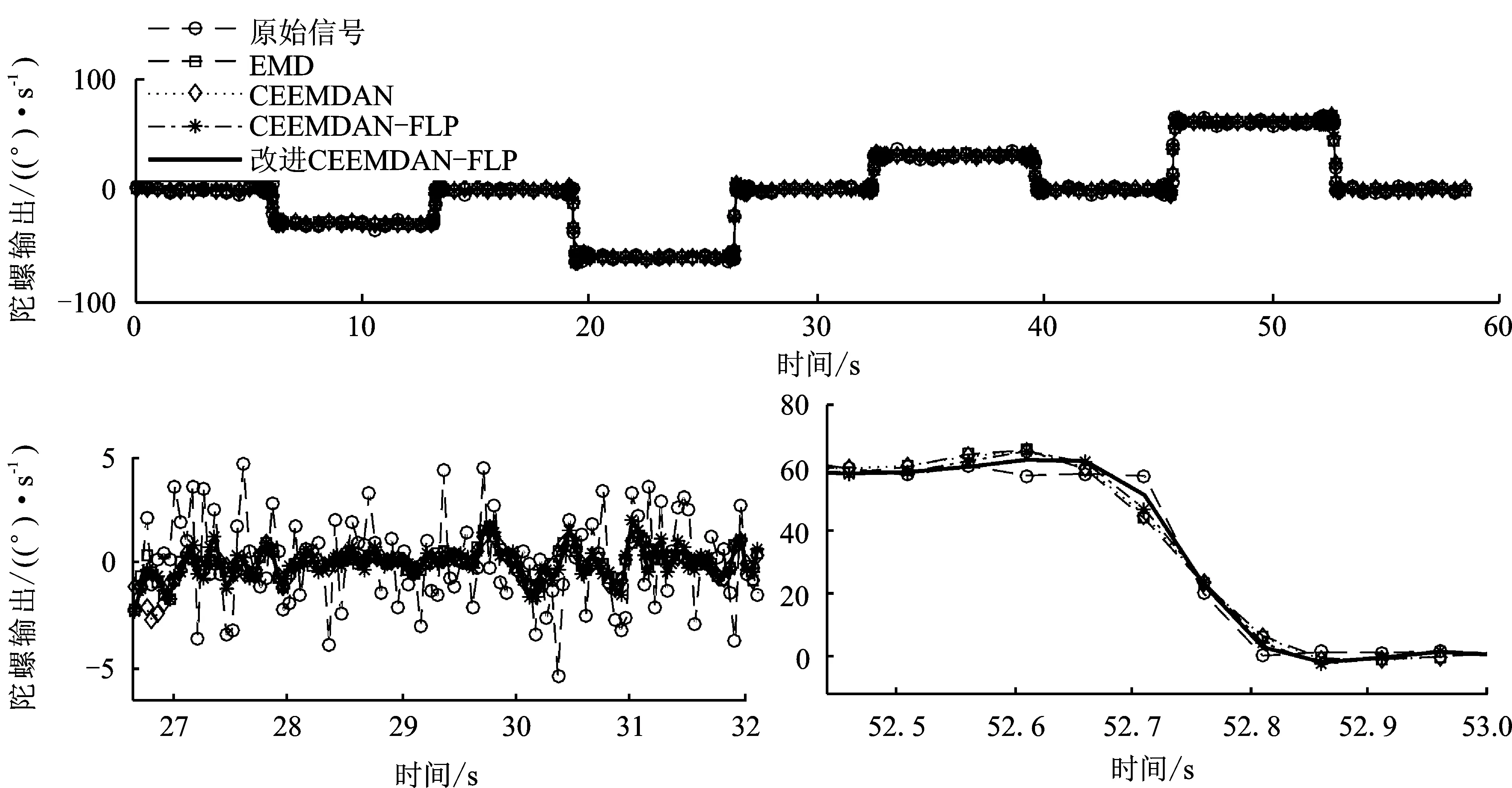
图6 仿真信号降噪前后对比图及细节放大图

与仿真理想数据误差统计对比结果如表1所示。改进的CEEMDAN-FLP滤波结果的均方根误差最小，仅为0.95°/s，而原始信号的均方根误差为1.96°/s，均方根误差较滤波前相比降低了约51.53%；基于EMD分解的滤波结果均方根误差为1.15°/s，改进算法与EMD滤波算法相比均方根误差降低了约17.39%；基于CEEMDAN分解的滤波结果均方根误差为1.12°/s，改进算法与CEEMDAN算法相比均方根误差降低了约15.18%。

表1 滤波前后误差统计对比 (°)/s

4 实验验证与分析

采集惯性导航模块的传感器数据，对仿真结果作进一步验证。陀螺采用ADXRS 645，传感器先处于静止状态，然后绕滚转轴以60°/s的速率旋转一周，静止20 s左右后，再逆向以60°/s的速率旋转一周，回到初始位置。实采数据通过改进CEEMDAN-FLP算法与EMD、CEEMDAN及CEEMDAN-FLP算法的滤波结果及细节放大图如图7所示。改进算法在信号突变处的延时最小，基于CEEMDAN-FLP算法和CEEMDAN算法在突变处的延时依次增大，而基于EMD的滤波算法信号延时最大，产生了信号失真。

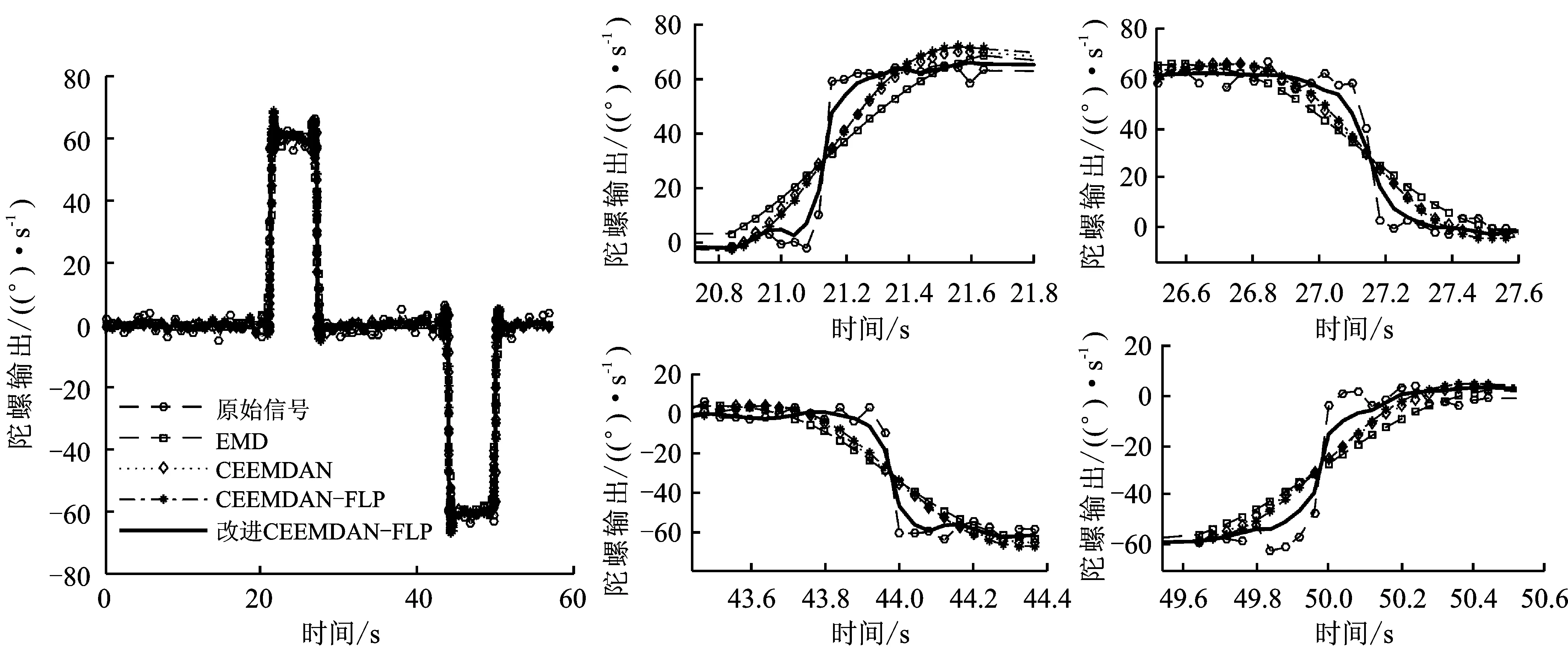
图7 实采信号降噪前后对比图及细节放大图

陀螺滤波前后数据与转台运动角速率误差统计对比结果如表2所示。改进的CEEMDAN-FLP滤波结果的均方根误差最小，仅为1.01°/s。基于CEEMDAN-FLP、CEEMDAN和EMD的滤波结果均方根误差依次增大。改进算法与原始信号相比，均方根误差降低了约57.02%；与基于EMD分解的滤波算法相比，均方根误差降低了约50.24%；与基于CEEMDAN的滤波算法相比，均方根误差降低了约38.04%；与基于CEEMDAN- FLP滤波算法相比，均方根误差降低了约35.67%。

表2 实采数据滤波前后误差统计对比 (°)/s

惯导模块正向旋转一周，在43 s处，理论姿态角应为360°，然后逆向旋转一周，在57 s处，理论姿态应为0°，对比分析正旋转(43 s处)和反旋转时(57 s处)改进CEEMDAN-FLP算法与EMD、CEEMDAN及CEEMDAN-FLP算法的滤波结果解算后的滚转角解算结果如图8所示。改进的CEEMDAN-FLP滤波算法解算的滚转角累积误差最小。

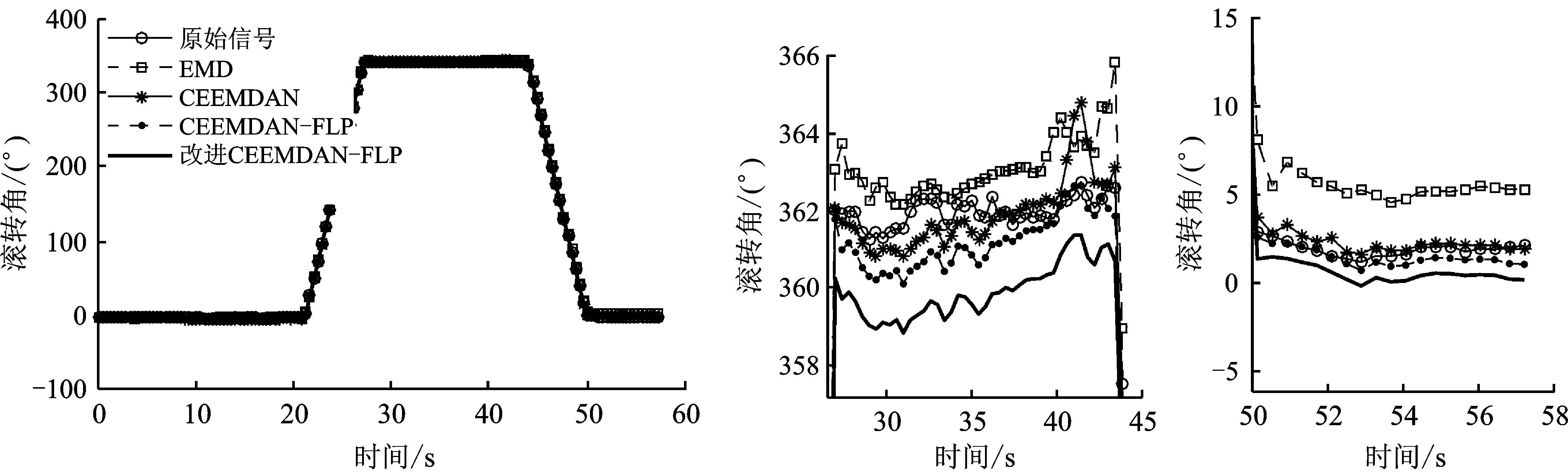
图8 姿态解算对比图及细节放大图

滚转角误差对比结果如表3所示。正转和反转结束后，改进CEEMDAN-FLP算法得到的滚转角误差为0.44°，误差最小；基于CEEMDAN-FLP滤波得到的滚转角误差为1.32°；基于CEEMDAN滤波得到的滚转角误差为2.14°。而基于EMD分解的滤波算法由于模态混叠引起信号失真，无法真实反映陀螺数据的变化情况，使得最终的滚转角解算结果甚至不及原始数据的滚转角解算结果。改进算法的姿态累积误差仅约为CEEMDAN滤波算法的20.56%，有效降低了姿态误差。

表3 姿态误差对比 (°)

在处理器为Intel Core i7-8550U、操作系统为Windows 10的笔记本电脑上，对实测陀螺数据进行处理，各个算法的运行时间对比如表4所示。基于EMD的滤波算法虽然耗时最短，但是模态混叠的问题限制了其应用；而基于CEEMDAN算法、CEEMDAN-FLP滤波算法和改进CEEMDAN-FLP滤波算法的时间消耗相当，通过仿真和实测数据验证，改进的CEEMDAN-FLP滤波算法的滤波降噪效果最好。

表4 算法运行时间对比 s

5 总 结

在惯性导航数据后处理中，针对当载体运动状态突然改变，导致MEMS陀螺传感器数据突变的情况，笔者提出了一种改进的CEEMDAN-FLP混合降噪方法。首先通过CEEMDAN算法将信号分解为多个IMFs 和一个趋势项，并将IMFs划分为噪声主导IMFs、信号噪声混合IMFs及信号主导IMFs。改进算法考虑了噪声IMFs的影响，对噪声IMFs和噪声信号混合IMFs分别采用软阈值(SIT)滤波和前向线性预测滤波(FLP)进行噪声消除，最后对滤波后的IMFs与信号IMFs及趋势项进行数据重构，在降噪的同时实现对高频信号的最大保留。将改进的CEEMDAN-FLP算法分别与基于EMD的滤波算法、基于CEEMDAN的滤波算法及基于CEEMDAN-FLP的滤波算法比较。通过仿真验证，改进算法滤波结果的均方根误差与滤波前相比减小了约51.53%，与基于EMD的滤波算法相比减小了约17.39%；通过实测数据验证，改进算法滤波后的陀螺数据与基于CEEMDAN的算法滤波后的陀螺数据分别用于姿态解算，在不明显增加运算负担的同时，改进算法姿态累积误差仅约是CEEMDAN算法姿态累积误差的20.56%，可见，改进算法可以有效提升姿态测量精度。