低复杂度LDPC码信息瓶颈量化译码器设计

胡继文，郑慧娟，童 胜，白宝明，徐达人，王仲立

(1.西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071；2.西安邮电大学 电子工程学院，陕西 西安 710121；3.阿里巴巴集团，浙江 杭州 311121)

低密度校验码(Low-Density Parity-Check，LDPC)码是一类性能优异的信道编码方案[1]。自上世纪90年代中期被重新发现以来，低密度校验码得到了学术界和工业界的广泛关注。目前，低密度校验码已经被国内外多个通信标准采纳，包括中国移动多媒体广播标准、WiMax、DVB-S2、IEEE 802.3以及最新的5G新空口等。在低密度校验码的实用化进程中，一个关键环节是高效低密度校验码译码器的设计。特别是在高端芯片受制的场合下，可通过算法层面突破限制，研发低实现复杂度、高性能量化译码算法，这是一条值得尝试的途径。

低密度校验码量化译码算法的设计涉及两方面[2]：一是对接收信号以及迭代译码过程中所传递消息的量化；二是译码算法中变量/校验节点局部运算的量化实现。消息的量化方案可以分为均匀量化和非均匀量化两种[3]：均匀量化实现简单，但是一般需要较大的量化位宽才能保证译码器的性能；相对而言，优化设计的非均匀量化方案在相同位宽条件下有望获得更好的译码性能。量化位宽是量化算法的关键因素，它极大地影响了量化译码器的译码性能。一般而言，量化位宽越大，译码性能越好。然而，文献[4]的研究表明，减少量化位宽可以带来众多好处：有效地减少存储空间，降低译码器硬件实现规模，提升运算速度，缓解现场可编程门阵列(FPGA)布线的拥塞问题等。因此，在保证可接受的译码性能前提下，低位宽量化方案的优化设计是量化译码器设计的关键问题之一。对于量化译码器设计的另一方面，即变量/校验节点的局部运算的量化实现，首先需要考虑的是译码算法的选择。通常有两种选择，即和积算法和修正最小和算法。和积算法性能优于修正最小和算法，但是它的运算复杂度也更高。特别是和积算法的校验节点运算涉及复杂的超越函数计算，不利于硬件实现。因此，许多硬件实现方案都以牺牲译码性能为代价选择计算复杂度更低的修正最小和算法[5]。

综上所述，基于性能更优的和积算法来设计低位宽高性能的低密度校验码量化译码器是具有实际应用价值的。近年来，已有一些学者将起源于信息论和机器学习领域的信息瓶颈(Information-Bottleneck，IB)[6]方法成功地应用于低密度校验码的量化译码器设计当中，获得了很好的效果[7-14]。基于信息瓶颈方法的低密度校验码量化译码器设计，以互信息为度量对消息(包括接收信号和迭代译码中传递的消息)进行量化处理，将所有消息都用无符号整型数进行表示，从而便于实际硬件实现。特别是在消息的量化过程中，以互信息最大化为优化目标。从保留信息量的角度看，基于信息瓶颈方法的量化方案是最佳的。此外，在校验节点消息更新的过程中，复杂的函数运算也通过信息瓶颈方法简化为简单的查表操作，从而大大地简化了运算复杂度。需要特别说明的是，在查找表的构建过程中，信息瓶颈方法以使得查表所得无符号整型数消息和其所代表的编码比特的互信息最大化为优化目标[7]，因此所构造的查找表在信息论意义下也是最佳的。由上所述，低密度校验码的信息瓶颈量化译码器是基于最佳的和积译码算法为基础设计的，并且在消息量化和节点量化实现两个方面均以互信息最大化为优化目标，是一种信息最佳量化译码器设计方法。这也就很好地解释了其译码性能的优异性。实际上，仿真结果表明基于信息瓶颈方法的4 bit低密度校验码量化译码器能够获得比未量化和积译码0.1 dB的优异性能。

近年来，对低密度校验码的信息瓶颈量化译码器的研究逐步深入，已经基本形成一套系统的设计方案。文献[7]中由和积算法推导了信息瓶颈量化译码器，并研究了设计信噪比对信息瓶颈量化译码器性能的影响。文献[8]中在数字信号处理器上实现了规则低密度校验码的信息瓶颈量化译码器，验证了其吞吐量优于最小和译码器。文献[9]中总结了规则低密度校验码的信息瓶颈量化译码器的设计流程，提供了一个通用的规则低密度校验码信息瓶颈量化译码器的设计框架，给出了寻找最佳设计信噪比的一种启发式方法，分析了量化位宽和码长对规则低密度校验码信息瓶颈量化译码器性能的影响。关于信息瓶颈方法在低密度校验码量化译码器中的更多应用可以进一步参考文献[10-14]。

虽然信息瓶颈量化译码器在存储空间、吞吐量以及译码性能方面都有很好的表现，但是仔细分析其译码过程，不难发现其局部节点运算中某些消息存在重复计算的现象，从而导致其查表次数与节点度数的平方成正比。为避免消息重复计算，笔者提出了一种基于前后向算法的信息瓶颈量化译码器优化设计方案。所提方案能有效地减少信息瓶颈量化译码器的查表次数，使得节点的查表次数从平方量级降低为线性量级。

1 信息瓶颈方法及其在低密度校验码量化译码器中的应用

1.1 信息瓶颈方法

信息瓶颈方法于1999年由TISHBY等[6]学者提出，它起源于信息论和机器学习领域，是一种适用于数据压缩的通用信息理论框架。信息瓶颈方法通过引入相关变量X，实现对观测变量Y进行数据压缩，从而得到压缩变量T，如图1所示。为此，信息瓶颈方法引入了两个目标：一是使互信息I(T；Y)最小化，即尽可能简洁地表示Y；二是最大化互信息I(T；X)，即尽可能让压缩变量T保留更多关于X的信息。变量X与变量Y通常是相关的，比如可以将Y看成是X经过信道传输后得到的观测值，它们的联合概率密度记为p(x，y)。变量T是由Y压缩而来的，即X→Y→T构成马尔可夫链。变量Y和T之间的压缩关系可以描述为Y到T的某种映射[9]，用概率论语言描述，这种映射可以表示为T与Y之间的条件概率分布p(t|y)。注意，上述压缩问题是一个双目标优化问题。为了便于求解，可以固定T取值空间的基数|T|，从而将所考虑的问题转化为单目标优化问题，即在给定|T|的前提下，寻找可以使得互信息I(T；X)最大化的映射p(t|y)[9]：

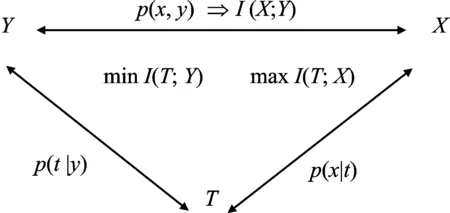
图1 信息瓶颈方法所研究的问题[10]

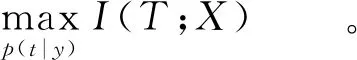
(1)

为了便于量化器实现，一个自然的要求就是给定一个观测值y，可以找到与之对应的惟一的压缩值t，即p(t|y)是一个确定性映射。这就意味着p(t|y)可以用某个函数t=f(y)来描述。

信息瓶颈算法是信息瓶颈方法的具体实现。如图2所示，在输入联合概率分布p(x，y)和T取值空间的基数|T|时，信息瓶颈算法会优化出确定性映射p(t|y)，以使互信息I(T；X)最大化[9]。自信息瓶颈方法提出之后，出现了适用于不同应用的多种信息瓶颈算法[9]。文献[9]给出了一种低复杂度的信息瓶颈算法，称为专用序贯信息瓶颈算法。由于该算法只优化量化区间的边界，其计算复杂度很低。在下面的信道输出量化和低密度校验码信息瓶颈量化译码器的构造过程中，都采用了该算法。由于篇幅受限，这里就不再赘述，有兴趣的读者可参考文献[9]。

图2 信息瓶颈算法[9]

下面将简要回顾文献[9]中原信息瓶颈量化译码器涉及的两个环节：信道输出信号的量化以及节点处局部运算的量化实现。

1.2 AWGN信道输出信号的信息瓶颈量化处理

这里考虑BPSK调制以及AWGN信道。编码比特b∈{0，1}经过BPSK调制后，映射成符号x=-2b+1，然后将x在AWGN信道上传递，在接收端得到接收信号y=x+n，n～N(0，σ2)。接收信号y和发送信号x的联合概率分布为

(2)

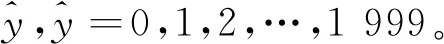
1.3 LDPC码IB量化译码器设计

本节简要回顾文献[9]中的信息瓶颈量化译码器设计方法。信息瓶颈量化译码器只涉及无符号整数，它以信道输出信号的量化值为输入，并以查表操作替代校验和变量节点的局部运算。

图3 度5校验节点拆分为3个度3校验节点的串联

(3)

综上所述，在每轮迭代中，一个度为dc的校验节点需要的查找表数目为(dc-2)。与之相连的dc条边都需要产生外信息，每条边涉及(dc-2)次查表操作，该节点共需要进行的查表次数为dc(dc-2)。这意味着查表次数与校验节点度数的平方成正比。这对于dc取值较大的LDPC码而言是不利的。

类似校验节点的信息瓶颈量化实现，变量节点的消息更新也可以利用信息瓶颈方法构造查找表来完成。具体实现方法不再赘述，可以参考文献[9]。度为dv的变量节点每轮迭代需要进行dv(dv-1)+1次查表。

值得一提的是，每轮迭代后，可以对变量节点取值做硬判决。由于对数似然比的分布是对称的，且其排序和离散消息取值的排序是一致的，只需要将变量节点的后验离散消息与|T|/2比较即可。

2 基于前后向算法的低密度校验码信息瓶颈量化译码器设计

2.1 基于前后向算法的信息瓶颈校验节点操作

(4)

(5)

(6)

为便于读者理解算法，下面以度7的校验节点为例进行说明，如图4所示。

(a) 前向查表过程

图5 低密度校验码FB-IB量化译码器校验节点输出外信息

由式(4)和式(5)可知，前向和后向查表共需要2(dc-2)次。为剩余(dc-2)条边生成外信息时，每生成一个外信息需要一次查表，所以输出外信息的过程需要(dc-2)次查表。因此，基于前后向算法的校验节点操作需要的查表次数为3(dc-2)，而原信息瓶颈量化译码器中一个度dc的校验节点需要dc(dc-2)次查表操作[9]，即查表次数从度数的平方量级降低到线性量级。显然，校验节点度数越大，降低的查表次数越可观。因此，该方法在高码率低密度校验码上具有较好的实用价值。

2.2 基于前后向算法的信息瓶颈变量节点操作

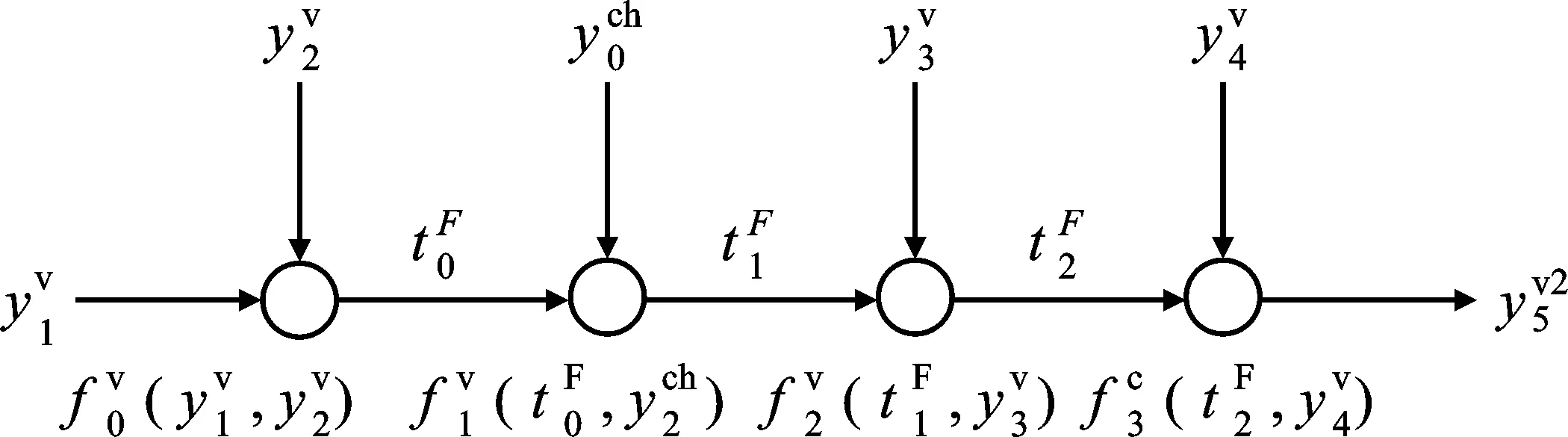
(a) 前向查表

3 复杂度分析及仿真结果

考虑一个规则低密度校验码，记其校验节点度为dc，变量节点度为dv。表1对比了笔者提出的方案和文献[9]的方案在一轮迭代过程中，局部运算各自需要的表格数目和查表次数。需要说明的是，两种方案所用单张表格的大小相同，且只与译码器的量化位宽相关。当采用量化位宽为q比特时，无符号整数T取值空间的基数|T|=2q。

表1 每轮迭代两种方案各自需要的表格数目和查表次数

笔者考查了802.3 an标准中的码率约为0.84的(2 048，1 723)低密度校验码[17]来验证所提方案。该码的校验节点度数dc=32，变量节点度数dv=6。按照表1的结论对比了该码使用文献[9]方案和所提方案设计的信息瓶颈译码器在单个节点更新消息时需要进行的查表次数，见图7(a)。从理论分析的角度可以看出，笔者所提的FB-IB量化译码器的查表次数远远低于原始图7 两种IB 译码器的性能对比方案。图7(b)比较了软件仿真5 000帧码字所需译码时间，验证了所提方案的有效性，其中仿真软件为Visual Studio 2017，编程语言为C语言。

(a) 查表复杂度对比

图8对比了(2 048，1 723)低密度校验码在不同量化译码算法下的性能。这里的仿真条件如下：BPSK调制下的AWGN信道，最大迭代次数为50。图8中floatSPA为双精度和积译码器，Qm.f量化SPA译码器使用的是来自文献[3]的均匀量化方案，其中m表示消息整数位使用的比特数，f表示消息小数位使用的比特数。信息瓶颈为文献[9]的方案，FB-IB为笔者所提方案。由图8可知，所提的4 bit FB-IB译码器与原4 bit信息瓶颈译码器的性能大致相当，且都明显优于6 bit均匀量化低密度校验译码器。当误码率为10-6时，所提4 bit FB-IB译码器以及原4 bit信息瓶颈译码器与双精度SPA译码器的译码性能差距不到0.1 dB。

图8 (2 048，1 723)LDPC码在不同译码算法下的性能比较

4 结束语

笔者提出了一种基于前后向算法的低复杂度LDPC码信息瓶颈量化译码器设计方案。该方案充分地利用了前向查表和后向查表产生的中间结果，有效地减少了查表次数。笔者以增加少量的空间复杂度为代价，所提设计方案可以将译码器的查表次数从平方量级降低到线性量级，更加适用于校验节点度数较大的高码率LDPC码。仿真结果表明，所提前后向信息瓶颈量化译码器的性能与原信息瓶颈量化译码器的性能相当，量化位宽为4 bit就可逼近未量化译码器的性能，验证了所提前后向信息瓶颈译码器的有效性。