复合材料板簧的模态预测与分析
2022-12-01刘鹤龙史文库陈志勇
刘鹤龙,史文库,高 蕊,陈志勇,陈 晃
(1.吉林大学 汽车仿真与控制国家重点实验室,长春 130022;2.中国重汽集团汽车研究总院,济南 250100)
纤维增强型复合材料由于具有比强度高、比模量大、耐腐蚀性好等优点,近年来在汽车的轻量化领域展现出了巨大的潜力[1-2]。以复合材料板簧替代钢板弹簧,不仅减重效果明显、降低能源消耗,而且能够减轻整车的非簧载质量,提高乘坐的舒适性和操纵稳定性。然而,板簧作为汽车悬架系统的主要弹性元件之一,在汽车行驶过程中,承受来自路面、发动机等复杂的振动激励。为了避免悬架系统的固有频率与外界激励频率耦合发生共振,需要在设计之初考虑板簧的模态特性,这对提高板簧的使用寿命以及提升整车NVH (noise,vibration,harshness)性能均具有重要意义。
目前,国内外学者[3-5]针对复合材料板簧的结构设计、疲劳等方面的研究较多,而与模态分析相关的报道较少。文献[6]利用锤击法和谱分析法对碳纤维复合材料(carbon fiber reinforced plastics,CFRP)板簧的模态进行了试验研究,发现了锤击法能够避免结构与激励单元之间的耦合问题,因此可以更准确的测试复合材料板簧的模态。文献[7-9]利用有限元软件对复合材料板簧的模态进行了预测,阐述了复合材料板簧的模态频率明显高于传统的钢板弹簧。文献[10]基于有限元软件建立了形状记忆合金(shape memory alloys,SMA)复合材料板簧的有限元模型,揭示了温度变化对SMA板簧固有频率的影响。文献[11]利用有限元软件建立了玻璃纤维复合材料(glass fiber reinforced plastic,GFRP)板簧的模态分析模型并进行了试验验证,同时利用该模型分析了各设计变量与复合材料板簧一阶模态频率之间的关系,得到了选用0°铺层角度、较低密度的复合材料和较高的纤维体积含量有利于降低复合材料板簧与激励发生共振的可能性的结论。有限元软件法由于在建模中能够考虑板簧的结构细节,因此计算的结果精度一般相对较高,但也存在着计算周期过长、建模以及模型的修改较为麻烦等弊端,不利于复合材料板簧的正向优化设计。因此,也有学者尝试利用理论建模的方法预测复合材料板簧的模态特性。文献[12]基于瑞利-里兹能量法建立了SMA复合材料板簧的模态频率的预测模型,并得到了板簧固有频率与温度、铺层角、SMA含量的关系曲线,但该模型计算相对复杂且缺乏试验验证,此外,一些关键设计参数与复合材料板簧模态之间的关系也还需要进一步的明确。文献[13]基于模态应变能法进行了复合材料板簧的结构健康检测,并指出所提方法能准确评价裂纹的存在、位置和严重程度,但所应用的模态理论模型过于简化,且未能考虑复合材料各向异性和铺层角度的影响。
因此,本文在前人的基础上,结合复合材料力学,基于微元法建立了复合材料板簧的模态预测模型,并试制了玻璃纤维/环氧复合材料板簧对模型的准确性进行了验证。最后,从复合材料的选材、铺层设计等角度出发,研究了相关参数对复合材料板簧模态的影响,能够为工程中的相关问题提供一定的参考。
1 复合材料板簧的结构
为了使板簧的轻量化效果最佳,同时又满足设计的刚度和强度要求,文献[14]经过优化指出,簧身的最优结构应从轴座到卷耳方向,宽度呈双曲线递增,厚度呈线性递减。但变宽度的复合材料板簧加工困难、浪费材料,因此文献[15]经过对各铺层长度的优化设计,得到了等宽变截面复合材料板簧的簧身结构厚度应从卷耳沿轴座方向近似呈抛物线形状增加的结论。相比于横置复合材料板簧,纵置复合材料板簧由于要考虑与车架车轴的连接问题,因此结构更为复杂。同时,考虑到加工成本与工艺的复杂性,一般纵置复合材料板簧不制造成接头-簧身一体化复合材料结构,而是由复合材料簧身、前金属接头、后金属接头、中部金属连接结构组成。
本文所研究的板簧为等宽变厚度的纵置复合材料板簧,具体结构如图1所示。其中:前、后金属接头通过螺栓与复合材料簧身连接,并辅以高强度的环氧树脂结构胶连接;中部金属夹板与簧身通过中心螺栓连接,并辅以胶接;板簧的两端金属接头的圆环代替钢板弹簧的吊耳与车架的吊耳销连接,而板簧中部通过中心螺栓实现与车轴定位并传递纵向力。
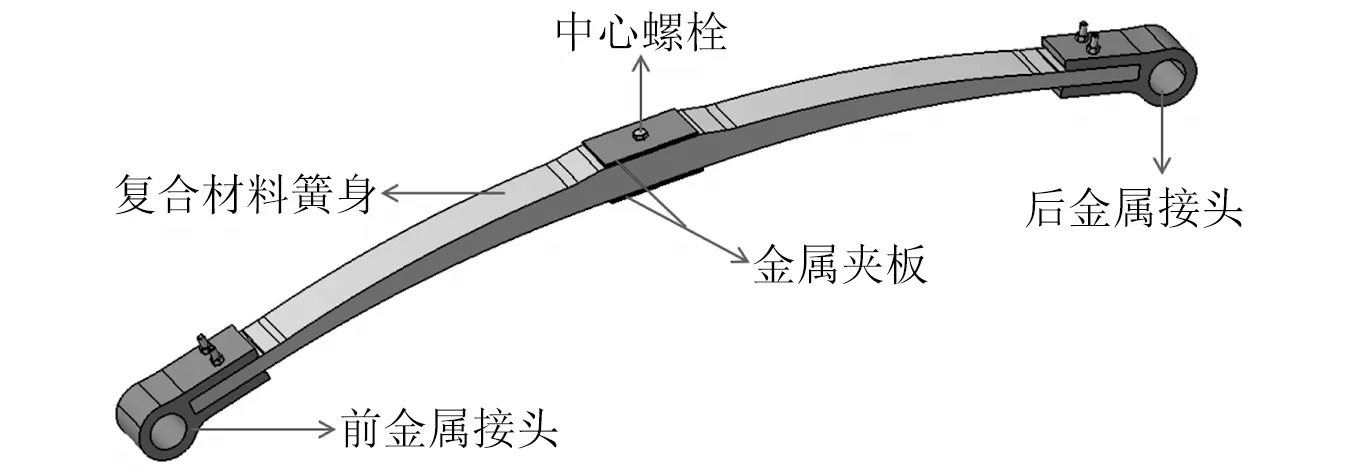
图1 复合材料板簧的结构Fig.1 Structure of the composite leaf spring
2 复合材料板簧的模态预测模型
2.1 单层板的工程弹性参数
明确材料的本构关系是结构设计的前提,纤维增强型复合材料属于正交各向异性材料,单层板的力学分析中主要包括两个弹性主方向,即1向(纤维方向)和2向(与纤维方向垂直),对应材料的刚度较大的主方向和刚度较小的主方向。1轴和2轴定义为材料的正轴,相应的1-2坐标系定义为材料的正轴坐标系,在1-2方向上测试得到的工程弹性参数为正轴工程弹性参数;复合材料结构的坐标系(x-y坐标系)与材料的正轴坐标系不重合时,定义x轴和y轴为单层板的偏轴,x-y坐标系为偏轴坐标系。当单层板受到正轴方向的应力时,正轴工程弹性参数可直接用于计算单层板的变形,而受到偏轴应力时,材料的偏轴工程弹性参数需要利用正轴工程弹性参数进行转换。
单层板的偏轴工程弹性参数可以根据式(1)计算得到
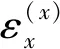
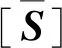
m=sinα,n=cosα
(3)
式中:E1,E2分别为1轴向和2轴向的正轴弹性模量;G12为面内正轴剪切模量;ν1和ν2分别为1轴向和2轴向泊松比,且满足ν1/E1=ν2/E2;α为铺层方向角,即x轴与1轴的夹角。
2.2 截面弯曲中性层位置的计算
板簧在发生弯曲变形时,截面一端承受拉应力;另一端承受压应力,中间不承受应力的位置定义为截面的弯曲中性层。相关研究表明,与各向同性材料不同,复合材料的拉伸模量与压缩模量可能存在差异[16];此外,根据式(2)可以看出,复合材料的偏轴弹性模量是铺层方向角的函数,板簧的实际铺层可能包含任意铺层方向角的单层,因此截面的弯曲中性层可能会相对于厚度方向上的几何中面发生偏移,这在计算板簧截面抗弯刚度及系统的刚度矩阵时不容忽视。
由于整个板簧存在复合材料簧身(只有复合材料)与金属连接件两部分,对于前、后接头以及中部金属连接区域,都可能存在金属-复合材料-金属的包夹段,因此选取包夹段进行中性层及截面抗弯刚度的推导。由于金属连接件与复合材料表面均采用高强度结构胶相连,故假设金属层与复合材料层接触表面没有相对滑动,且截面中复合材料部分与金属部分的曲率半径相同。
纯弯曲截面变形前后如图2所示。其中:p,q分别为截面中受拉、压金属层的厚度;j为截面中复合材料部分的厚度;aa为几何中面;oo为中性层。
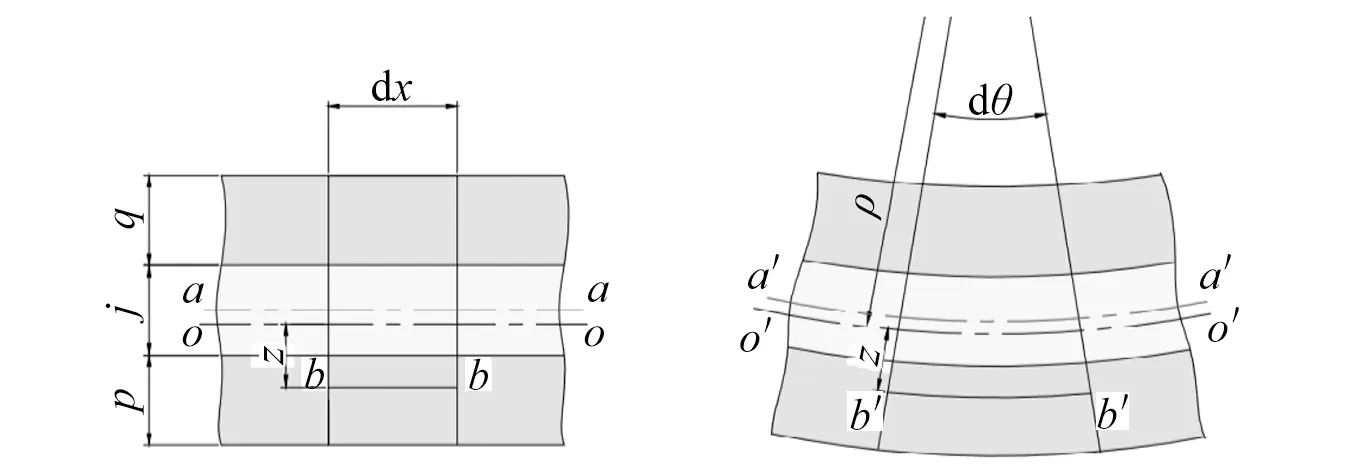
图2 截面弯曲变形Fig.2 Section bending deformation
根据平面假设,变形前相距dx的两个横截面,变形后相对旋转了一个角度dθ,并仍保持平面。距中性层距离为z的纵向纤维bb的长度变为

(4)
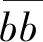

(5)
根据应变的定义,求得纤维bb的应变为
(6)
对复合材料板簧的任意一个截面A,沿x轴方向的力可表示为
(7)
定义中性层位移系数λ如下
(8)
式中:d为中性层与几何中性层之间的距离;t为该截面的厚度,且满足
t=p+j+q
(9)
则对于厚度为j的复合材料区域,第k层单层距中性层的距离zk为
(10)
式中,δ为复合材料单层厚度。
以中性层为原点位置,拉为正、压为负,式(7)可以展开为
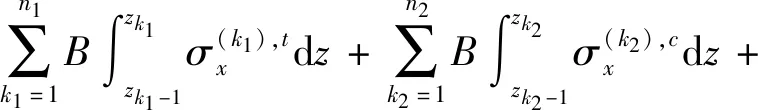
(11)
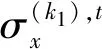
(12)
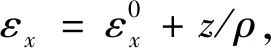

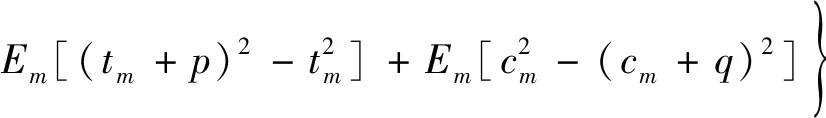
式中:Em为金属材料的弹性模量;在复合材料板簧受力为纯弯曲情况下,有
FN=0
(14)
故有
(15)
联立式(10)、式(12)、式(15),即可解得中性层位移系数λ。
2.3 截面抗弯刚度的求解
对于复合材料板簧簧身垂直于x轴的任意一个截面,其受到绕y轴的弯矩可表示为
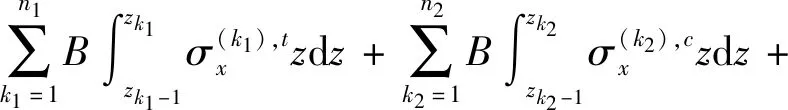
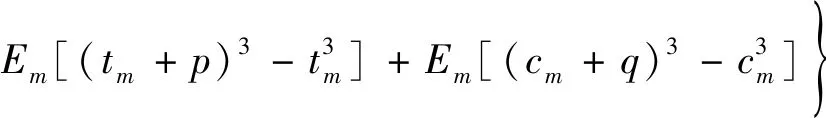
设截面抗弯刚度为D,则
(17)
即有
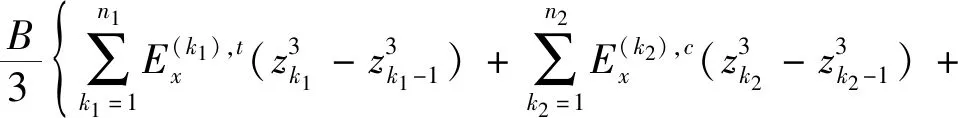
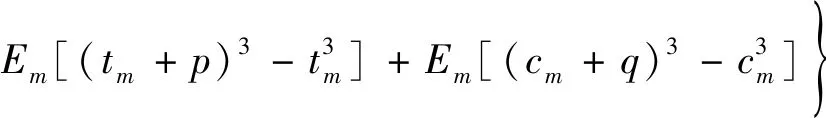
值得说明的是,式(18)能够通过对不同数量的单层的刚度特性求和来获得对应不同厚度截面的抗弯刚度。当计算复合材料簧身部分,即不存在金属连接件时,则p=q=0。
2.4 微元法建立复合材料板簧模态预测模型
模态的求解,即对系统的固有频率及对应振型的求解。n自由度系统自由模态的特征方程为
(19)
式中,K,M分别为系统的刚度矩阵和质量矩阵,一般为n×n阶的对称常数矩阵。板簧在工作过程中,主要承受整车与路面之间的垂向载荷。为了减少分析的自由度,减低问题的复杂度,仅对复合材料板簧的垂向自由模态进行预测。根据微元法的思想,将板簧的整体结构沿长度方向划分为若干个单元,每个单元的两端各有垂向位移与旋转两个自由度,相邻单元的共有端存在相同自由度的约束。
当单元的φA为常数时,单元的的质量矩阵为
(20)
式中:φ为板簧截面的材料密度;A为截面面积;le为单元长度;当单元内部的截面抗弯刚度De为常数时,单元的刚度矩阵为
(21)
将整个板簧沿长度方向划分为i个单元,则系统的独立坐标转换前的刚度矩阵与质量矩阵为
(22)
由于相邻单元存在两个相同自由度的坐标,因此在整体坐标系下,独立坐标数量为nd=2i+2。因此,
(23)
式中,β为独立坐标转换矩阵,可以根据边界条件获得,且满足β∈R4i×nd。
根据式(23)确定系统的刚度矩阵和质量矩阵后,便可由式(19),基于MATLAB软件中矩阵特征值的求解函数得到复合材料板簧系统的固有频率和对应的振型。
3 复合材料板簧模态预测模型的验证
采用有限元法和试验法验证模态预测理论模型的正确性。GFRP板簧试验样件如图3所示。板簧簧身为等宽变截面形状,从吊耳沿中部近似呈抛物线形状增加。铺层角度均为0°,复合材料层合板的密度为1 990 kg/m3,金属材料的弹性模量为206 MPa,密度为7 850 kg/m3。

图3 复合材料板簧样件Fig.3 Composite leaf spring samples
复合材料板簧的两端金属接头与中部的连接结构包含较大比重的金属材料,以集中质量的方式处理可能造成较大的计算误差,因此需要对接头部分进行较合理的等效处理。为简化计算,对于前后金属接头的吊耳圆环部分,等效为长方体块状结构,且等效前后与原结构长度、质量、密度一致;对于中部连接结构,除了较少部分的螺栓连接结构外,结构较为均匀,为了简化运算,等效为均匀的包夹段,且总质量、尺寸与原结构一致,等效的结构如图4所示。

图4 复合材料板簧等效结构示意图Fig.4 Equivalent structure of the composite leaf spring
相关结构参数如表1所示。复合材料层合板的力学性能参数,如表2所示。理论模型中沿板簧长度方向所划分单元的长度对模态频率的预测结果的影响,如表3所示。从表3中可以看出,在分析范围内所划分单元的长度对复合材料板簧弯曲模态频率预测结果的影响较小。由于本文的复合材料板簧的铺层长度均为整数,因此为了保证划分的单元能更准确的体现板簧的变截面几何形状,同时兼顾计算的效率,本文的后续分析将所划分单元的长度取为1 mm。
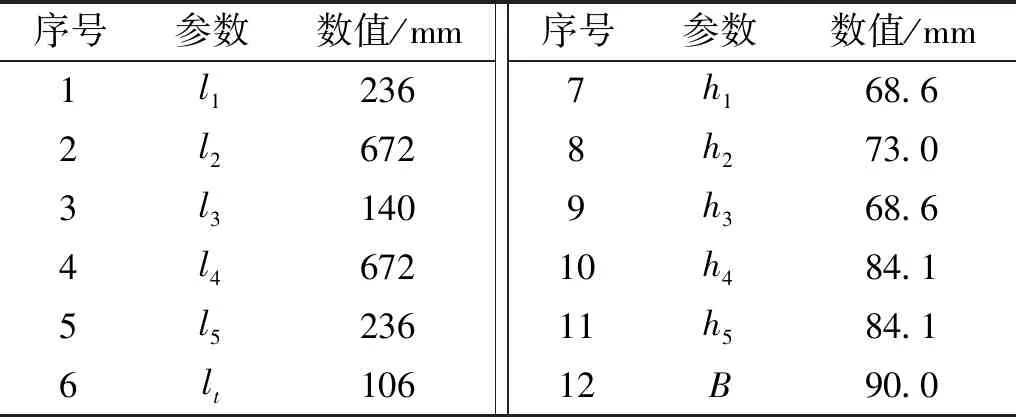
表1 复合材料板簧的结构参数Tab.1 Structural parameters of composite leaf spring

表2 复合材料层合板的力学性能参数Tab.2 Mechanical property parameters of composite laminate
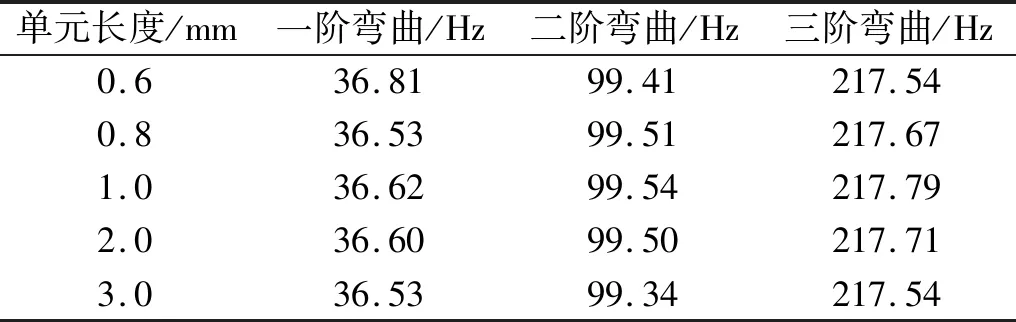
表3 单元长度对模态频率的影响Tab.3 Influence of element length on frequency results
利用锤击法对复合材料板簧的自由模态进行测试。试验采用LMS TEST.LAB测试系统及B &K三向振动加速度传感器进行测量,在复合材料板簧的簧身两侧布置传感器,由于传感器数量有限,采用多点分区测量。板簧的悬挂状态如图5所示。对刚度较大的端部和中部的金属接头位置分别进行锤击,最后将锤击点所测得的结果进行综合分析,得到复合材料板簧的各阶试验模态频率与振型。

图5 复合材料板簧的悬挂状态Fig.5 Suspension state of composite leaf spring
利用ABAQUS软件对复合材料板簧总成进行模态分析。三种方法所得的前三阶弯曲模态振型如图6所示,各阶模态振型对应频率对比如表4所示。

图6 三种方法得到的模态振型对比Fig.6 Comparison of modal shape between three methods

表4 三种方法得到的模态频率结果对比Tab.4 Comparison of the frequency results obtained by three methods
由图6可知,模态试验、理论预测与有限元分析的模态振型基本一致;由表4可以看出,复合材料板簧第3阶弯曲模态频率接近200 Hz,远大于路面激励频率和发动机怠速激励,因此本文取前三阶模态进行分析能够满足工程实际需要,理论预测的复合材料板簧的前三阶弯曲频率均与试验结果、有限元分析接近,其中理论预测的前三阶频率与试验结果的误差分别为2.46%,3.27%和6.84%,误差较小,因此可以认为该数值模型能够实现对复合材料板簧的模态预测,有助于缩短复合材料板簧正向开发的周期。
4 复合材料板簧模态影响因素分析
在复合材料板簧各阶弯曲模态中,与发动机怠速激励、路面激励频率最为接近的为一阶弯曲振动,因此本文以复合材料板簧的一阶弯曲振动模态频率为研究对象,从选材、铺层等设计角度出发,分析复合材料板簧各关键参数对其模态特性的影响。本文主要研究铺层角度α、复合材料的弹性模量E、复合材料的密度φc、板簧簧身宽度B对复合材料板簧模态频率的影响。
采用控制变量法进行分析,即在分析某个参数对板簧的一阶弯曲模态频率的影响规律时,其他设计参数与算例中的参数一致。分析铺层角度α对板簧模态频率的影响时,假设各单层方向角的绝对值相等,且均为α,以[+α/-α]的形式循环铺层,影响趋势如图7所示。从图7中可以看出,铺层角度对板簧的一阶弯曲固有频率的影响较大,在0°铺层时,固有频率最高,在0°~55°左右时,频率下降较快,而55°~85°时,板簧频率整体略有增加,但幅度较小,而85°~90°趋于平缓。由此可见,选用0°铺层能有效提高板簧的固有频率。

图7 铺层角度对板簧一阶弯曲模态频率的影响Fig.7 Influence of ply orientation on bending frequency
复合材料层合板的弹性模量E对板簧模态频率的影响,如图8所示。图8中,E0为材料的初始模量。从图8可以看出,复合材料层合板的弹性模量对板簧固有频率的影响较大,弹性模量越大,板簧的固有频率越高。因此,选用弹性模量大的复合材料有利于提高板簧的固有频率。
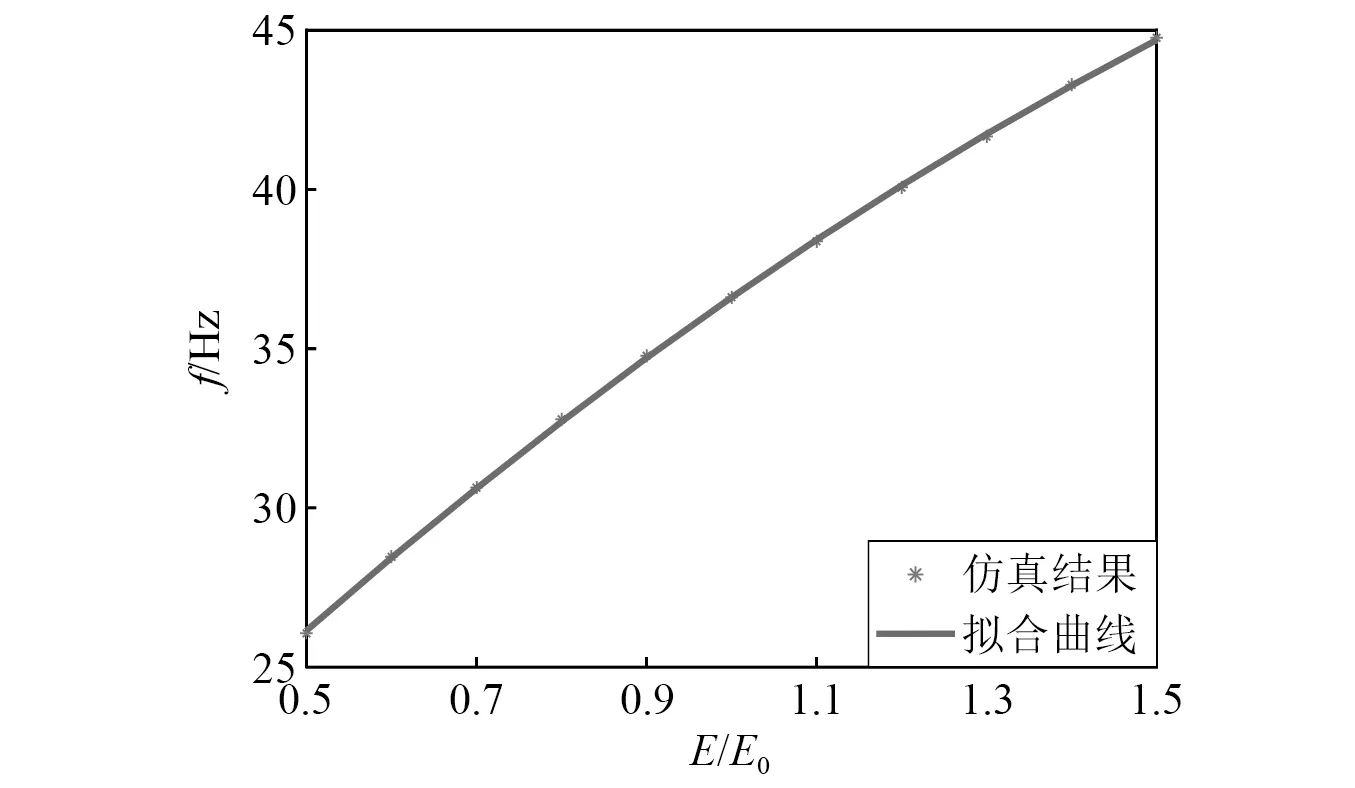
图8 复合材料弹性模量对板簧一阶弯曲模态频率的影响Fig.8 Influence of elastic modulus on bending frequency
复合材料层合板的密度φc对板簧模态频率的影响,如图9所示。图9中,Δφc为材料的密度相对初始密度的变化量。从图9可以看出,板簧的固有频率与复合材料层合板的密度呈负相关趋势。因此,选用密度较小的复合材料有利于提高板簧的固有频率。
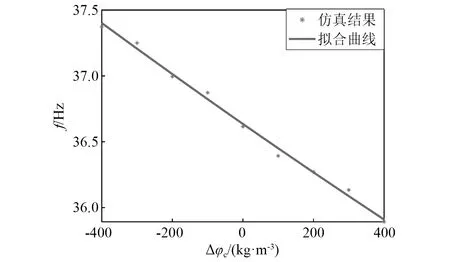
图9 复合材料层合板密度对板簧一阶弯曲模态频率的影响Fig.9 Influence of composite density on bending frequency
簧身宽度B对板簧模态频率的影响,如图10所示。图10中,ΔB为簧身的宽度相对初始宽度的变化量。从图10可以看出,增加簧身宽度有利于提高板簧的固有频率。
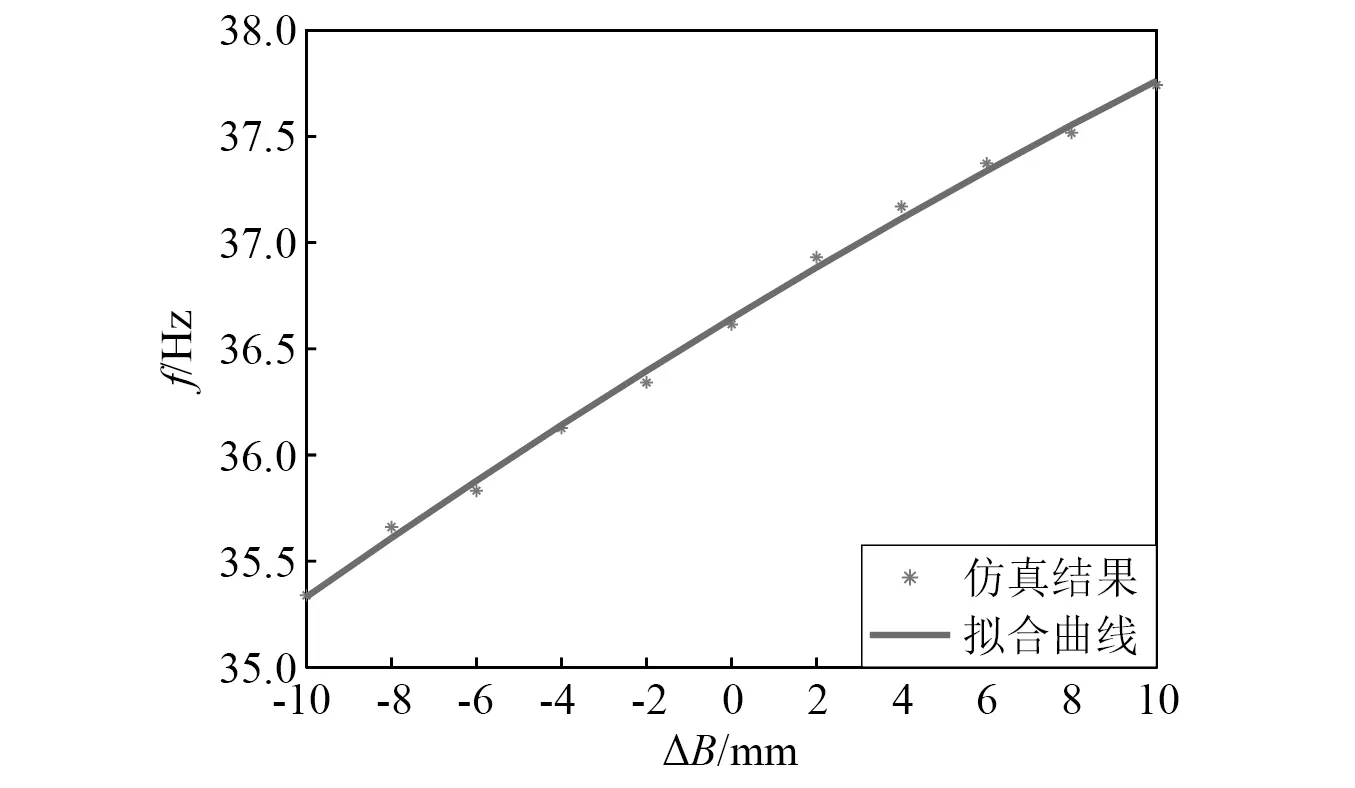
图10 簧身宽度对板簧一阶弯曲模态频率的影响Fig.10 Influence of body width on bending frequency
5 结 论
(1)本文基于微元法和复合材料力学,建立了复合材料板簧的模态预测理论模型,该理论模型能够避免常规有限元软件分析过程中繁琐的建模、网格划分等过程,有利于提高计算效率,同时也便于结合复合材料板簧的其他性能实现对板簧的参数化优化设计、缩短复合材料板簧的正向开发周期。
(2)铺层角度对板簧模态影响较大,0°铺层时板簧垂向弯曲固有频率最大,在满足其他要求的前提下,选用密度较低、弹性模量较大的复合材料,并尽可能增加簧身宽度,有利于提高弯曲模态频率、降低板簧与外界激励耦合共振的可能性。
