少片根部加强型抛物线板簧的刚度与应力解析计算
2019-12-11王凤娟周长城于曰伟张云山邵明磊
王凤娟,周长城,于曰伟,张云山,汪 晓,邵明磊
(1. 山东理工大学 交通与车辆工程学院,山东 淄博 255049;2.山东弹簧厂淄博有限公司,山东 淄博 256410)
随着汽车轻量化相关政策的实施,少片变截面钢板弹簧日益受到汽车悬架研究领域专家及生产企业的重视。 为了满足板簧设计的刚度要求和应力约束条件,通常在板簧根部平直段与抛物线段之间增设斜线段结构,且由于首片板簧端部所受载荷复杂,须使首片板簧的端部平直段厚度和长度的设计值大于其余各片,即采用端部非等构式的少片根部加强型抛物线板簧。 目前,国内外很多学者借助于有限元仿真分析法[1-2]、多体动力学仿真分析法[3]和板簧试验法[4-6]等对少片变截面钢板弹簧力学特性进行了研究。 其中,针对少片钢板弹簧轻量化优化设计方法的研究,有学者采用CAE建模仿真和板簧台架试验,对少片钢板弹簧力学特性刚度和应力进行对比分析[7-10];有学者采用Adams/Chassis Leaf spring专业模块的二次开发模型,对悬架钢板弹簧进行力学特性试验和不同工况下的仿真分析[11];有学者采用ANSYS有限元仿真软件和样机试验相结合的方法对钢板弹簧的刚度、应力等力学特性进行研究[12-15]。 然而,上述研究方法都未给出精确的少片根部加强型抛物线板簧刚度及应力解析计算式,不能满足板簧现代化CAD设计以及数字化工厂的要求,这给少片变截面板簧的精准设计与产品开发带来了不便。
本文基于单片根部加强型抛物线板簧力学模型,对其刚度及应力进行解析计算,在此基础上建立少片根部加强型抛物线板簧的刚度及应力计算公式,通过实例对所建立的少片根部加强型抛物线板簧刚度及应力计算公式进行解析计算和ANSYS仿真验证。
1 单片根部加强型抛物线板簧的刚度及应力解析计算
1.1 单片根部加强型抛物线板簧结构及力学模型
单片根部加强型抛物线板簧对称结构力学模型如图1所示,其由根部直线段、斜线段、抛物线段和端部直线段四部分构成,板簧自由端处所受单端点载荷为F,长度为L,宽度为b,弹性模量为E;根部厚度为h2,根部直线段为安装间距的一半,其长度为l3;斜线段的厚度比为γ,其水平长度为Δl,斜线段部分厚度为hd(x),其根部至板簧自由端处长度为ld;抛物线段的厚度比为β,厚度为hp(x),近根部端处厚度为h2p,其根部至板簧自由端处长度为l2;端部长度为l1,厚度为h1;坐标原点O在模型右部自由端处,水平向左指向x轴正方向。
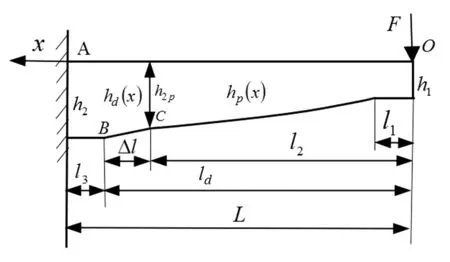
图1 单片根部加强型抛物线板簧力学模型Fig.1 Mechanics model of single-chip root-intensive parabolic leaf spring
根据图1所示的单片根部加强型抛物线板簧的力学模型,板簧端部厚度h1为
h1=βh2p=βγh2
(1)
式中:β=h1/h2p;γ=h2p/h2。
板簧端部直线段长度l1为
l1=(βγ)2l2
(2)
板簧抛物线段部分厚度hp(x)为
(3)
根部斜线段部分过(l2,h2p)、(ld,h2)两点,则板簧根部斜线段部分厚度hd(x)为
(4)
综上,单片根部加强型抛物线板簧的厚度表达式h(x)为
(5)
1.2 单片根部加强型抛物线板簧刚度及应力的解析计算
当在板簧端部施加载荷F时,其变形能为
(6)
式中:I1、I2、I3、I4分别为板簧端部直线段、抛物线段、斜线段、根部直线段部分的截面惯性矩,其中
(7)
根据卡式第二定理,板簧端部挠度为
(8)
将式(5)—式(7)代入式(8)整理可得,单片根部加强型抛物线板簧的挠度解析计算式为
(9)
式中:Gd为单片根部加强型抛物线板簧的挠度系数,其表达式为
由单片板簧刚度、挠度与载荷的相互关系可知,单片根部加强型抛物线板簧的刚度解析计算式为
(10)
单片根部加强型抛物线板簧在x位置处的弯矩M(x)为
M(x)=Fx
(11)
由材料力学可知,板簧在x位置处的应力为
(12)
式中:W(x)为板簧抗弯截面系数,即W(x)=bh2(x)/6。
将式(5)代入式(12)整理可得,单片根部加强型抛物线板簧的应力计算模型为
(13)
2 少片根部加强型抛物线板簧的刚度及应力解析计算
少片根部加强型抛物线板簧由单片根部加强型抛物线板簧叠加而成,其力学模型如图2所示。少片根部加强型抛物线板簧端部为非等构结构,即首片板簧的端部直线段的厚度和长度大于其他各片板簧,使得首片板簧能够满足端部复杂受力的需求。 板簧片数为n(n≤5),弹性模量为E。 各片根部加强型抛物线板簧的根部厚度为hi2,抛物线段近根部端处厚度为h2pi,端部厚度为hi1,端部长度为li1=(βiγi)2l2,斜线段厚度比为γi,抛物线段的厚度比为βi。
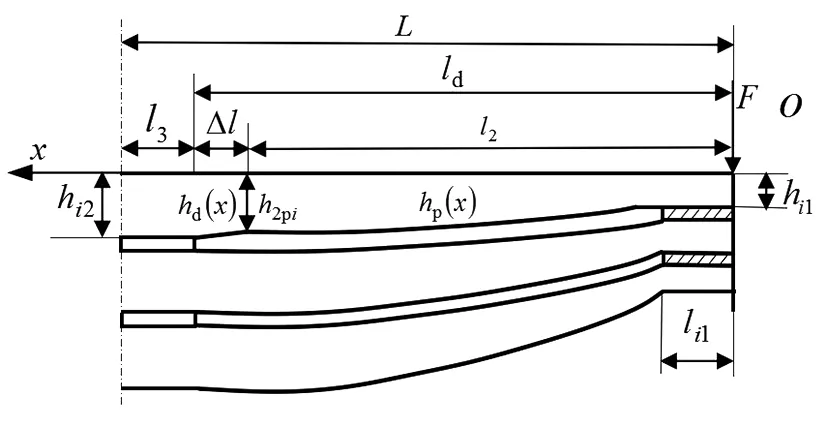
图2 少片根部加强型抛物线板簧力学模型Fig.2 Mechanics model of few-chip root-intensive parabolic leaf spring
由式(10)可得,少片根部加强型抛物线板簧的各片加紧刚度Ki为
(14)
式中:Gdi为加紧状态下的各片板簧挠度系数,有
其中,βi=hi1/h2pi,γi=h2pi/hi2。
因此,少片根部加强型抛物线板簧的加紧刚度计算式为
(15)
在端部载荷F的作用下,少片根部加强型抛物线板簧的挠度wmax为
(16)
由式(13)可知,在加紧状态下,少片根部加强型抛物线板簧的各片板簧任意位置处的应力计算式为
(17)
式中:Fi为各片板簧端部所受载荷,基于各片板簧刚度Ki与载荷Fi之间的关系,有
3 解析计算实例和仿真分析
3.1 解析计算实例
某款车型前悬架板簧采用少片根部加强型抛物线板簧,弹簧片数n=3,板簧宽度b=70 mm,弹簧一半长度L=600 mm,U型螺栓中心距的一半l3=44 mm,根部平直段厚度hi2=17 mm,根部斜线段水平长度Δ=30 mm,抛物线段近根部端处厚度为h2pi=15.98 mm;端部直线段厚度分别为h11=8.79 mm、h21=h31=8.32 mm,长度分别为l11=159.12 mm、l21=l31=142.64 mm;各片板簧抛物线段厚度比为β1=8.79/15.98=0.55,β2=β3=8.32/15.98=0.52,各片板簧斜线段厚度比为γi=15.98/17=0.94,板簧端部所受单端点载荷F=8146 N,弹性模量E=200 GPa。
由式(14)可得,该根部加强型抛物线板簧的各片加紧刚度Ki为
式中,加紧状态下的各片板簧的挠度系数Gdi为
Gd1=106.11 mm4/N,
Gd2=Gd3=108.18 mm4/N
因此,该板簧的加紧刚度为
K=274.2 N/mm
该板簧在端部载荷F=8146 N下的挠度为
少片根部加强型抛物线板簧的各片端部所受载荷为
由式(17)可得,各片板簧在任意位置处的应力为
σ2(x)=σ3(x)=
在端部载荷F作用下,各片板簧在不同位置处的应力变化曲线分别如图3和图4所示。
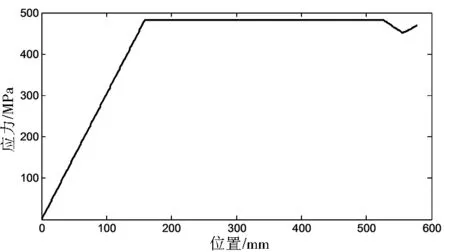
图3 第1片板簧应力变化曲线Fig. 3 Stress changing curve of first-chip leaf spring
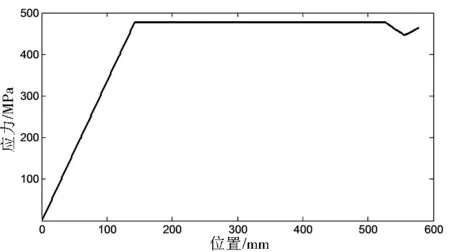
图4 第2、3片板簧应力变化曲线Fig. 4 Stress changing curve of second and third chip leaf spring
由图3和图4可知,各片根部加强型抛物线板簧在端部直线段随位置x的增加其应力呈线性上升趋势,在抛物线段部分应力不变且应力值最大,根部斜线段处的应力随位置x的增加呈直线下降,根部直线段处的应力随位置x的增加呈线性增加趋势. 由于首片板簧端部直线段的厚度与长度大于其余各片,使得第1片板簧最大应力大于第2、3片板簧。根部斜线段结构使得各片板簧应力降低,起到改善板簧强度的作用. 由于根部斜线段结构的存在,使得各片板簧最大应力出现在根部位置处或抛物线段部分。
3.2 仿真分析
利用ANSYS仿真软件对上述少片根部加强型抛物线板簧进行静力学特性仿真,并与解析值进行对比分析。 通过Contacts确定各片板簧模型之间的接触区域,设置接触类型为No Separation,各片板簧根部直线段之间设置为面与面接触,端部位置处设置为线与面接触;在划分网格时,通过Sizing进行网格尺寸的相关设置,在Relevance Center设置中选择Fine,使几何模型的节点数量与单元数量增加,以达到细化网格的目的;在Element Size中选择Element Size=4 mm,通过网格尺寸大小来控制几何尺寸网格划分的粗细程度。 其中,该板簧的网格模型如图5所示。

图5 少片根部加强型抛物线板簧网格模型Fig. 5 Mesh model of few-chip root-intensive parabolic leaf spring
在首片板簧端部上边缘位置处沿Y方向施加集中载荷F=8146.3 N,在各片板簧根部截面位置处施加固定约束,并对模型进行求解,分别给出该板簧在Y方向的变形云图和各片板簧沿X方向的应力云图。 其中,变形云图如图6所示,可知,该板簧在集中载荷F=8146.3 N作用下的挠度为wmax=58.94 mm。
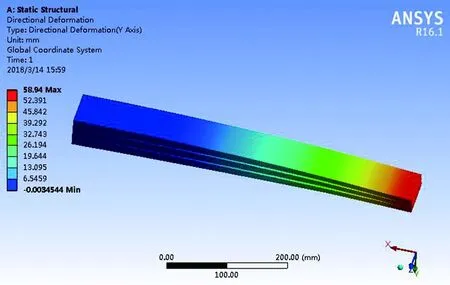
图6 少片根部加强型抛物线板簧变形云图Fig. 6 Deformatione nephogram of first-chip root-intensive parabolic leaf spring
同时,对该板簧挠度及刚度的解析结果与仿真结果进行分析,见表1。
表1 板簧挠度及刚度结果分析
Tab. 1 Deflection and stiffness analysis of leaf spring

参数挠度/mm刚度/N·mm-1解析值59.4274.2仿真值58.94276.4相对偏差值/%0.780.80
由表1可知,该少片根部加强型板簧挠度、刚度的解析值与仿真值的相对偏差值在0.80%范围内,结果分析表明,所建立的少片根部加强型抛物线板簧挠度和刚度解析式是正确的。
各片板簧的应力云图及其在抛物线段部分的应力分别如图7和图8所示。由图可知,第1片板簧抛物线段部分的应力为484.51 MPa,第2、3片的为478.46 MPa。
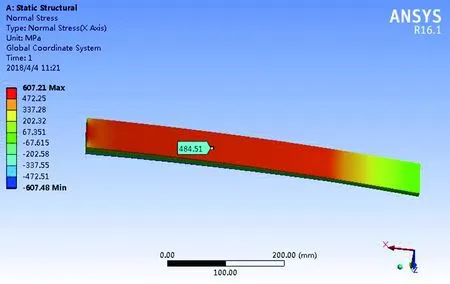
图7 第1片板簧应力云图 Fig. 7 Stress nephogram of first-chip leaf spring

图8 第2、3片板簧应力云图Fig.8 Stress nephogram of second and third chip leaf spring
同时,对该板簧在抛物线段部分的应力解析值与仿真值进行对比,其结果见表2。
表2 板簧应力结果分析
Tab. 2 Stress analysis of leaf spring

参数第1片/MPa第2、3片/MPa解析值485.71476.26仿真值484.51478.46相对偏差值/%0.250.46
由该板簧的应力云图和表2可知,该少片根部加强型抛物线板簧各片最大应力并非在根部位置处,根部斜线段结构使得各片板簧最大应力在抛物线段部分;该板簧各片应力解析值与其仿真值的相对偏差值均在0.5%范围内,对比结果表明,所建立的少片根部加强型抛物线板簧任意位置处的应力计算式是正确的。
4 结论
(1)基于单片根部加强型抛物线板簧力学模型,结合板簧厚度表达式,利用卡氏第二定理,推导出了单片根部加强型抛物线板簧挠度和刚度计算公式。 由材料力学,结合板簧端部所受载荷,建立了单片根部加强型抛物线板簧应力计算公式。
(2)根据少片根部加强型抛物线板簧刚度等于各片板簧刚度之和,利用板簧挠度、刚度及所受载荷的相互关系,建立了其刚度计算公式;依据各片板簧端部所受载荷与刚度的关系,建立了其各片板簧任意位置处的应力计算公式。
(3)由解析计算实例和ANSYS仿真验证可知,少片根部加强型抛物线板簧的挠度、刚度及任意位置处的应力解析值与其仿真值均相吻合,相对偏差均在0.80%以内。 仿真结果表明,所建立的板簧挠度、刚度及任意位置处的应力计算公式是精确的,这对少片根部加强型抛物线板簧的优化设计具有一定的指导意义。
