Lamb波的交叉递归分析在金属板损伤量化中的应用
2022-12-01刘小峰张天瑀孙小强
刘小峰,张天瑀,孙小强 ,柏 林
(重庆大学 机械与运载学院,重庆 400044)
金属板材作为一种基础构件广泛应用于航空、航天、船舶、石油化工及兵器工业等领域。由于环境腐蚀、温度改变、碰撞冲击,外部载荷等因素的作用,长期服役的金属板不可避免地出现疲劳损伤,随着时间的推移,材料内部的微裂纹或微缺陷不断聚合发展,逐渐形成宏观损伤,最终导致结构失效[1-2]。因此,对金属板的疲劳损伤进行检测并进行量化评估对保证结构服役安全具有重要意义。Lamb波是在自由板中产生的平面应变波,它具有对结构微小损伤敏感,衰减慢,传播范围广等优点,非常适用于板材结构的健康监测与损伤检测[3]。
目前,基于超声导波的结构损伤量化分析方法,主要是采用接收信号波形变化参数对结构损伤状态进行表征,主要包括导波透射系数法(透过损伤后的波形幅值与无损情况幅值的比值)[4-5]、损伤反射系数法[6]、时间差值法[7]及波数变化法[8]等。Li[9]通过轴向传感器阵列获得的管道Lamb波损伤信号,采用二维盲卷积方法估计了管道裂纹的大小。Wang等[10]根据非线性Lamb波的谐波幅值与基频幅值计算出的金属材料非线性参数,对金属材料疲劳裂纹进行了评估。Tse等[11]根据缺陷回波特点,将两个相互重叠的 Gabor原子构造成新的匹配原子,通过优化两个 Gabor之间的距离,估计了管道轴向缺陷大小。要指出的是,上述这些方法大都需要对损伤波包进行辨识分离,但Lamb波传播机理复杂,具有频散性与多模态性,且在环境噪声的干扰下早期损伤波包十分微弱,这些因素都使得损伤波包或损伤特征信息的提取极具挑战性。
为了实现微弱缺陷信号的增强,许多研究者采用了时间反转聚焦方法[12]、共源方法[13]、相控聚焦方法[14]、虚拟反转聚焦法[15]等来提高Lamb波信噪比、增强缺陷信号,但这些技术不仅实际操作步骤复杂,而且在聚焦过程中容易出现其他的杂波,影响损伤检测结果。文献[16-17]采用混沌振子对金属铝板早期裂纹产生的微弱非线性波包进行了检测,采用Lyapunov指数、相轨迹面积指数对损伤程度进行了量化分析。这种混沌系统检测方法往往对系统参数设置非常敏感,且不适应于强噪干扰下的结构损伤检测。
金属板构件的损伤演变过程通常是非线性的,金属板在不同的损伤状态下具有不同的动力学特性。交叉递归分析是一种直观定量表达两种及其以上非线性过程之间联系的可视化工具,可用于非线性动力学系统定向分析,揭示非线性时间序列的内部结构。这种方法对系统动力学特性的变化非常敏感,在生理病理信息提取[18]、机械设备故障诊断[19]、歌曲识别[20]等方面都得到广泛的应用,特别适合于结构健康监测中的损伤评估。本文旨在通过对金属板Lamb波信号的交叉递归分析实现金属板疲劳损伤量化评估的目的。本文的主要贡献在于,在对金属板Lamb信号进行CRQA特征提取的基础上,结合特征的状态相关性、单调性、鲁棒性及特征间的关联性对CRQA特征进行了优化选择,并采用支持向量数据描述(support vector data description,SVDD)模型对优选特征进行了融合,构建了能够表征金属板损伤状态的统一量化指数。
1 基于CRQA的统一损伤指数
1.1 交叉递归图
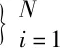
(1)
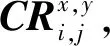
1.2 CRQA特征
虽然CRP可以较为直观地观察两个系统状态的递归特性及其相似性,但递归图结构往往复杂,不便于状态信息的量化分析,因此可采用式(2)~式(10)中的递归量化特征来测定递归图中的基本图形点和线段的分布特征。
递归率(recurrence rate,RR),代表了递归图中递归点的密度,也是量化系统发生递归行为最为直接的一个指标。
(2)
确定性(determinism,DET),代表了对角线结构的递归点与所有递归点的比率。
(3)
平均对角线长度(average line length of diagonal lines,ADL),代表具有这种相似性在动力学系统中的持续时间。
(4)
最长对角线(length of the longest diagonal line,LD),代表了输入信号经过相空间重构后,其相轨迹发散的趋势,发散越快则对角线越短。
(5)
对角线长度熵(entropy,ENTR),递归图相对于对角线复杂性的一种量化。
(6)
分层性(laminarity,LAM),递归图中构成垂直线的递归点数目与整个递归点集合的比率。
(7)
捕获时间(trapping time,TT),代表了垂直线的平均长度。
(8)
最长垂直线的长度(length of the longest vertical line,LV),代表了递归图中最长对角线的长度。
(9)
Ⅰ型递归时间(recurrence time of 1st type,RT1),动力学系统完成递归需要的时间。
DRT1=|{i,j∶xi,yj∈Ri}|
(10)
1.3 特征选取
为了实现CRQA特征对金属板损伤的一致性表征,有必要对各个特征进行表征性能评价与优化选择。状态相关性、单调性及鲁棒性是评价系统或结构性能退化特征有效性的主要指标,分别表述为
(11)
(12)
(13)
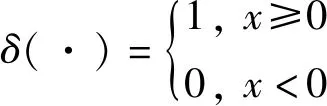
Corri(fi,di)表示特征fi与损伤程度di间的相关系数,fi的相关性指标越大,说明特征与损伤程度相关性越强,越能更好描述损伤程度。单调性Mon(fi)用于描述损伤演化的一致性,其值越接近1说明该特征在结构损伤演化过程中越能保持良好的单调趋势。鲁棒性指标Rob(fi)用于评价特征的抗干扰性,特征序列越平滑说明其鲁棒性越好,对损伤状态的评估的不确定越小。另者,选择具有一致性状态表征能力的特征进行融合,有助于得到稳定的统一损伤指数。因此,本文采用了KL距离来衡量两个特征fi与fj之间的分布相似性
(14)
式中,fi,k为特征fi在损伤程度dk处对应的取值。两个特征的KL散度距离越小,表明两者的分布越相似,对损伤状态的表征能力越接近。将特征fi与其他特征间的KL距离之和作为该特征在整个特征集合中的关联度的评价指标,即
(15)
综合考虑特征的状态相关性、单调性、鲁棒性、特征间关联度,采用式(16)的综合评价指数对损伤特征进行筛选。
Ev(fi)=ωi·(Moni+Corri+Robi)
(16)
式中:Ev(fi)越大,表示特征fi对损伤的综合表征能力越强;反之,亦然。
1.4 统一损伤指数构建
为了能够对金属板损伤程度进行统一表征,有必要将优选出的CRQA特征进行融合,建立统一的损伤指数。本文引入SVDD方法建立一个包容无损特征样本的最小超球体边界。超球体之内表示为无损样本,超球体之外视为损伤样本,且损伤样本偏离超球体中心的距离正表征了损伤的程度。设无损状态下的特征训练集合为S={xi,i=1,2,…,l},I为样本数。设法建立一个以o为中心,以R为半径的能够包含所有无损样本点的最小球体,优化问题[21]为
(17)
约束为
(18)
式中,C为惩罚参数。对于一个新的测试样本实例xw,其离超球体中心o的归一化距离可表述为
d=‖xw-o‖2
(19)
则统一损伤指数(damage index,DI)定义为
(20)
金属板损伤程度越大,则DI值越大。从以上分析可知,本文提出的DI指数无需考虑Lamb波多模态、散射性与噪声干扰性,无需对复杂Lamb波信号进行时域或频域的损伤波包识别与特征提取,而是从结构动力学角度对信号进行整体递归分析,得到能够表征金属板损伤状态的DI指数。
2 仿真模型验证
2.1 仿真模型描述
为了验证CRQA方法的有效性,在ABAQUS平台下建立400 mm×20 mm×1.5 mm的条状铝板有限元模型,如图2所示。铝板材料参数为:ρ=2 704 kg/m3,E=6.89×1010Pa,υ=0.33。在铝板模型中心区域设置有N条随机均匀分布的闭合式裂纹,每条裂纹的中心位置与角度均采用均匀随机概率密度函数。对于含裂纹模型,裂纹面考虑为接触,可以张开,但是不能相互穿透。采用库伦摩擦准则计算摩擦力来模拟裂纹面的相互滑动,采用4节点平面应变单元(CPE4R)进行网格划分,裂纹区进行网格细化,保证每个裂纹面上至少含有6个单元。在模型左端施加激励信号,使得在薄板中能够激发S0模式Lamb波,激发的信号为汉宁窗调幅的正弦信号,其周期数为10,中心频率为500 kHz,幅值为2×10-4mm距离激发点250 mm处接受检测信号。
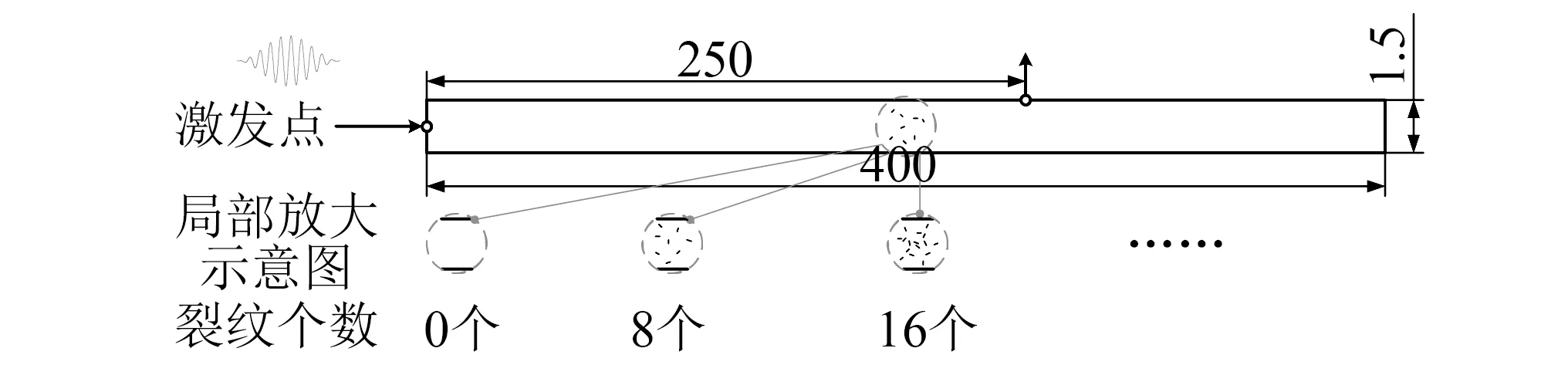
图1 铝板裂纹损伤模型(mm)Fig.1 Simulation model of aluminum plate cracks(mm)
信号激发与接收环境不变,取裂纹数N分别为0、8、16、24、32、40、48、56、64和72共10组有限元模型所接收信号作为不同损伤程度的铝板检测信号进行分析。分析信号长度均为 1×10-4s,采样频率为 25 000 kHz。
2.2 仿真信号特征提取
以N=0时仿真模型接收的Lamb波信号为基准,计算其他模型信号与基准信号的交叉递归图。图2给出了N=0,N=24,N=48以及N=72时仿真信号对应的CRP。可以看出,无损情况下的CRP具有较大的递归域,即黑色区域。不同裂纹个数下的Lamb波信号构成的CRP对角线结构与递归点数存在明显差异。随着裂纹个数的增加,CRP中的递归点密度下降,递归区域越来越小,垂直与水平线也越来细,表明损伤状态与无损状态的铝板动力学特性差异性越来越大。
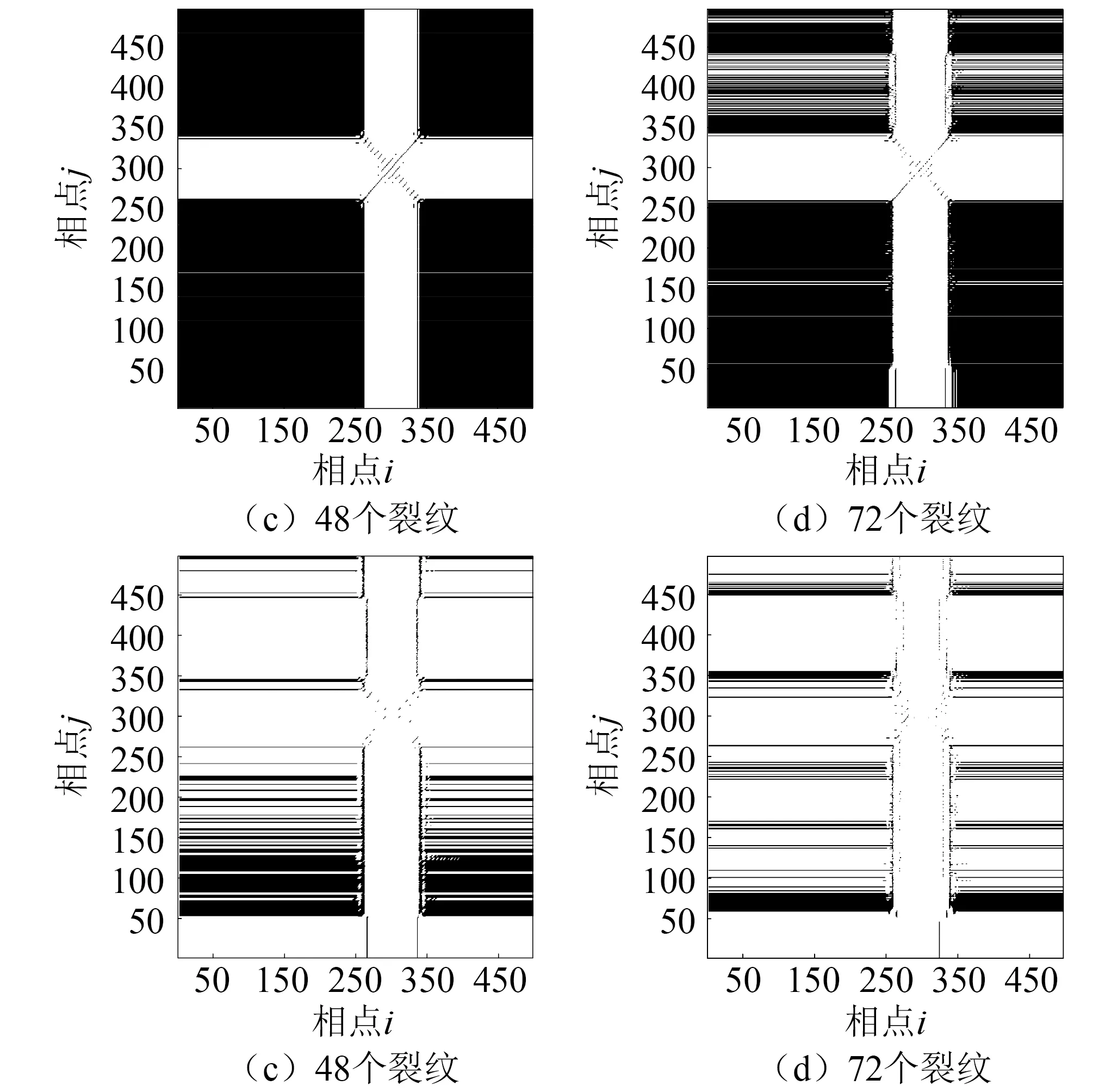
图2 仿真模型信号交叉递归图Fig.2 Cross-recurrence plot of FEM signals
为了对铝板损伤状态进行量化分析,根据式(2)~式(10)提取各个损伤状态下CRP的CRQA特征(RR、DET、ADL、LD、ENTR、LAM、TT、LV及RT1),并根据式(11)~式(16)计算各个特征的综合评价指数Ev,如图3所示。由图3可以看出,其中4个指数明显高于其他指数,因此筛选出的新特征向量集为{RR,DET,LAM,RT1}。
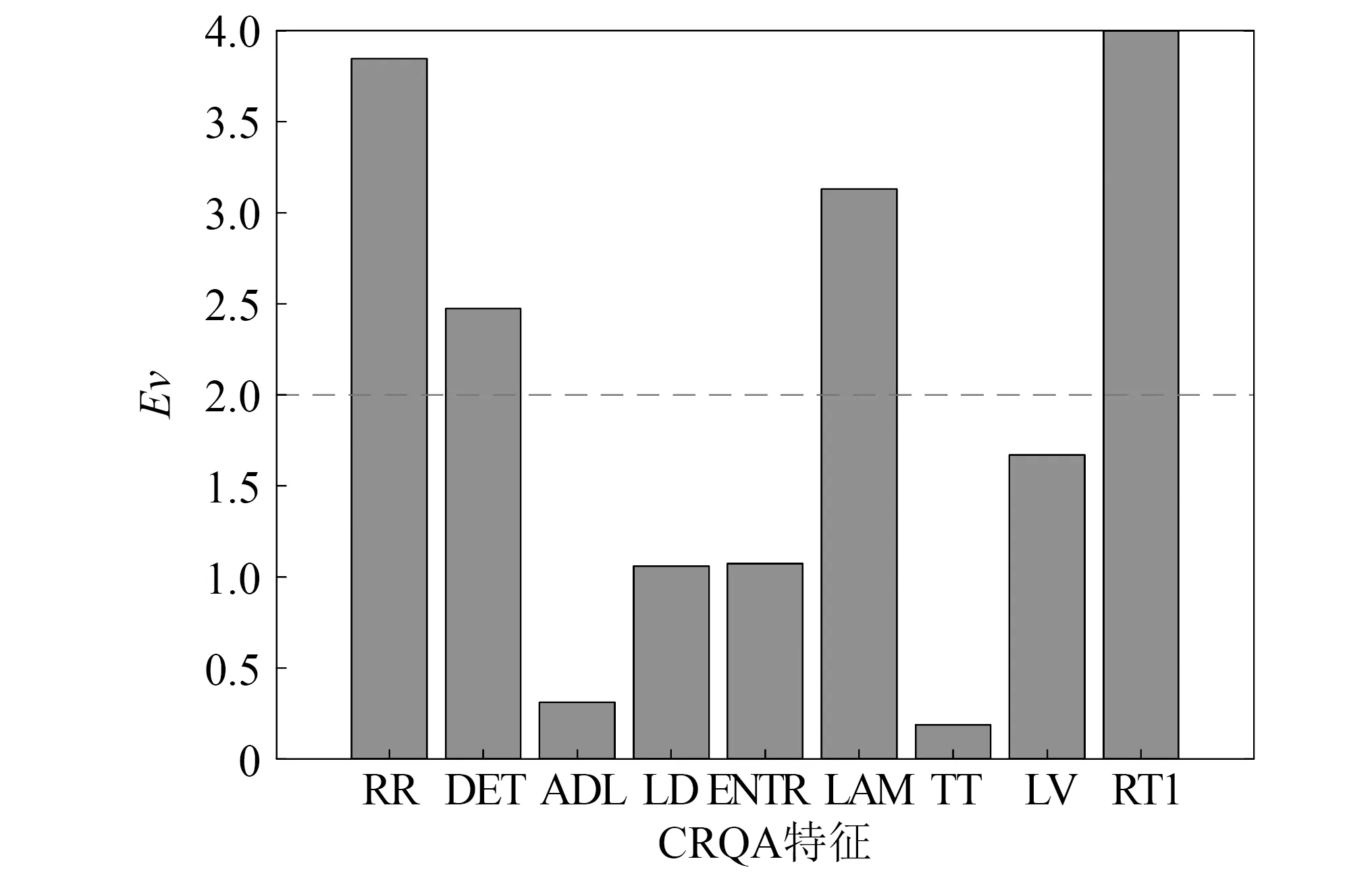
图3 CRQA特征的综合评价指数Fig.3 Evaluation values of CRQA features
图4给出了优选出的特征与裂纹个数关系的线图。图4(a)与图4(d)中的RR与RT1两个特征都分别随着裂纹个数变化而呈现线性递增与递减趋势,尽管图4(b)与图4(c)中的DET与LAM与裂纹个数间没有绝对的线性相关性,但基本趋势是随着裂纹个数的增加而变小的。这主要是因为,金属板的损伤程度不仅与裂纹个数有关,与裂纹深度、方向、位置等分布信息有关系,且每个CRQA特征所表征的损伤信息是有限的。因此,有必要对多个损伤特征进行融合,采用统一的损伤指数对铝板损伤进行一致性表征。
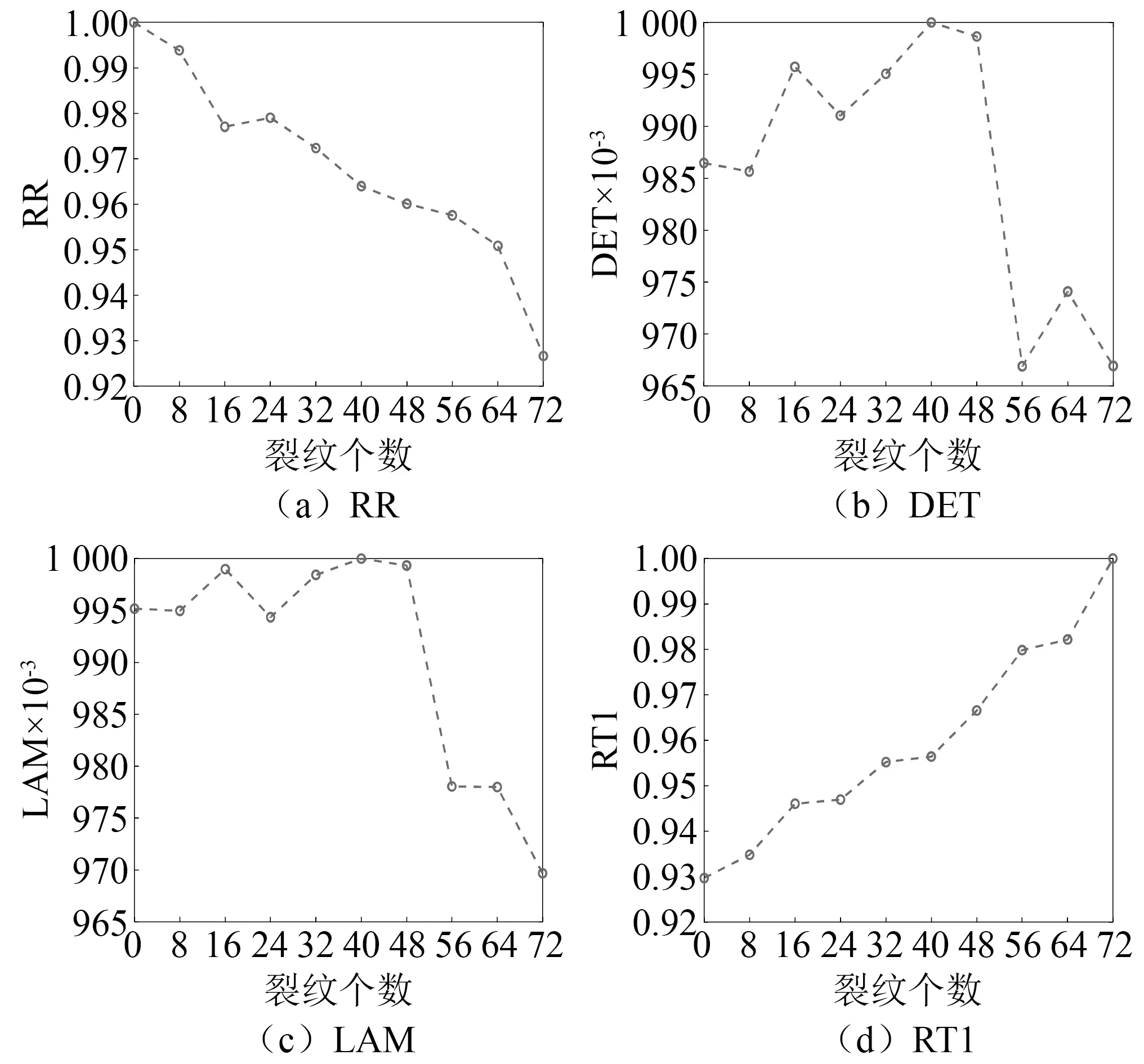
图4 仿真信号CRQA特征Fig.4 CRQA features of simulation signals
2.3 裂纹程度量化分析
为了模拟噪声环境影响下的测试信号,将不同强度的白噪声加入无损仿真模型获得的Lamb波信号中,产生10个噪声影响下的无损信号样本。以这10个样本的CRQA特征向量{RR,DET,LAM,RT1}为训练样本,建立SVDD模型,根据式(19)~式(20)计算其他9个损伤模型的统一损伤指数DI,结果如图5(黑色实线)所示。可见,融合后的DI曲线随着裂纹个数单调递增,呈现了较好的趋势性和平滑性,对铝板损伤的具有更好的表征能力。
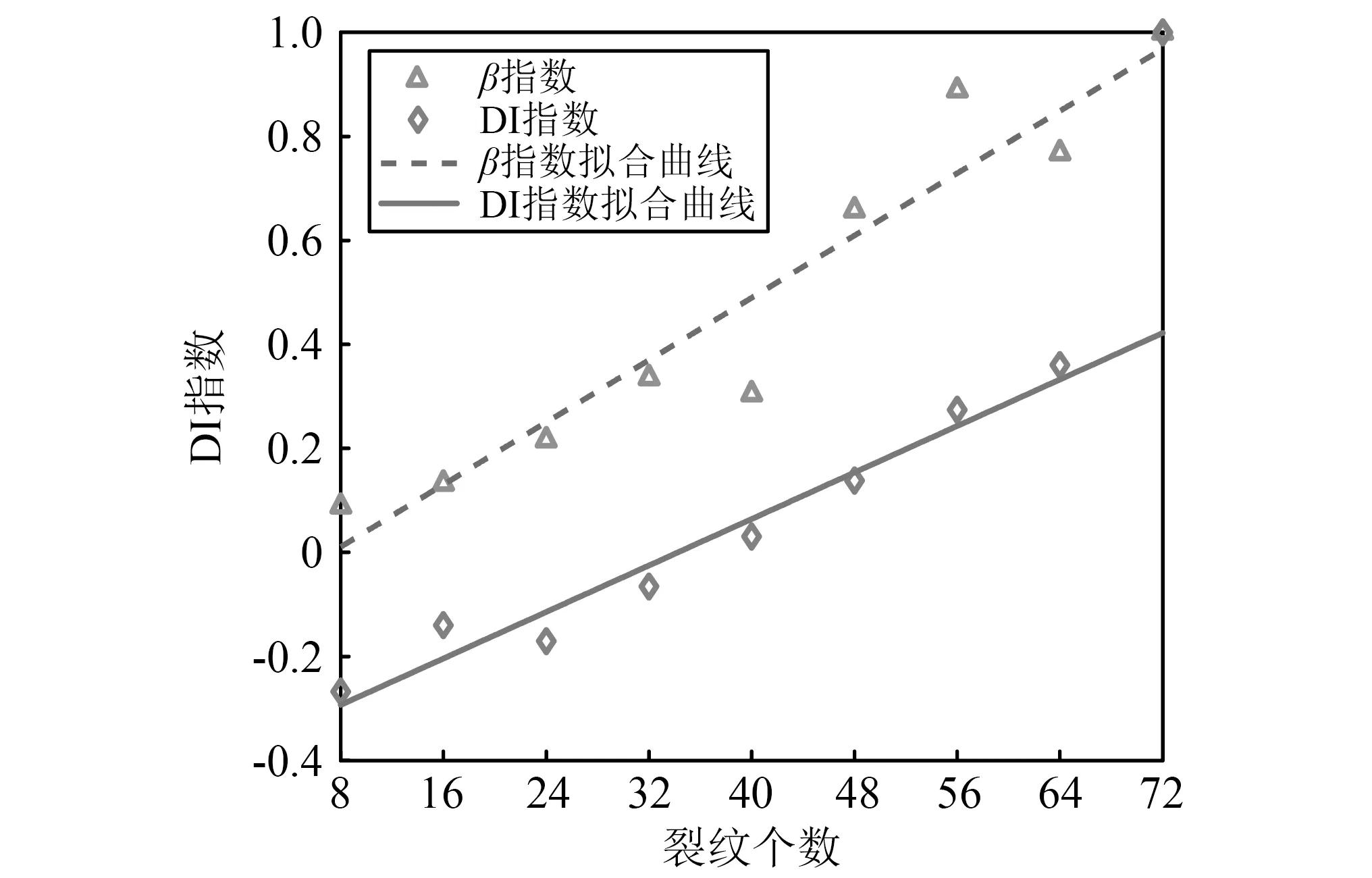
图5 仿真模型统一损伤指数Fig.5 United damage index of FEMs
铝板的闭合式裂纹损伤一般可采用 Lamb 波非线性参数[22]来表征,即,β=A2/A1,其中:A1为Lamb波信号在激发频率处的幅值;A2为2倍频率处的幅值。图5(黑色虚线)呈现了β随裂纹个数的变化关系。较于β,DI在其线性拟合直线周围的分布更加均匀,与裂纹个数具有更好的线性相关性。要指出的是,在裂纹数量为72时,由于铝板中裂纹密度太大,破坏了传播介质的连续性,Lamb波穿过裂纹区域后波包能量锐减与波形畸变,导致提取的DI指数在72个裂纹时的奇异点。
为了进一步验证本文提出的DI指数对铝板损伤表征的噪声鲁棒性,对各个仿真模型产生的Lamb波信号中分别加入20 dB与10 dB的白噪声,计算加噪信号的统一损伤指数DI与β系数。采用式(21)中R-square指数和式(22)中的RMSE分别对这两个损伤指数与裂纹个数间的线性相关性进行评估,结果如表1所示。
(21)
(22)

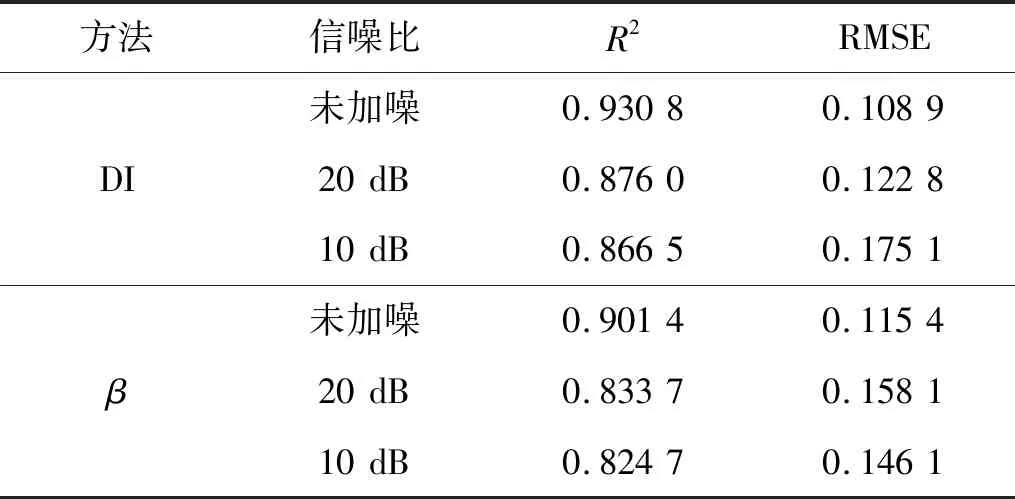
表1 仿真模型损伤指数比较Tab.1 Comparison of FEM damage indexes
3 试验应用
3.1 试验描述
为了进一步验证本文提出方法的有效性,采用铝板局部弯曲塑性破坏试验进行验证。选择材料为Al-6061,尺寸为2 400 mm×20 mm×2 mm的铝板进行弯折损伤试验,环境温度控制在22±1 ℃。首先将铝板加载使其逆时针弯曲90°保持5 s,然后再反转加载使其顺时针弯曲180°保持5 s。上述加载方式需重复循环10次。工件每次弯折后进行一次Lamb检测,检测装置的配置如图6所示。通过信号发生器AFG3102生成汉明窗调制正弦信号,周期数为10,中心频率为200 kHz,振幅为4 V。信号生成后经过AG系列功率放大器放大信号,再通过压电陶瓷换能器连接到铝试样上以产生S0模态兰姆波进行激发。激发点和接收点位于铝板中心点两侧50 mm处,激光测振仪PSV-500获取Lamb波损伤信号。
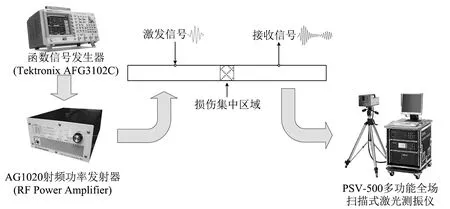
图6 试验装置示意图Fig.6 Schematic diagram of experiment setting
3.2 损伤信号递归量化分析
以试验铝板9次弯折得到的损伤信号与弯折前的无损信号为分析对象,计算损伤信号与无损信号间CRP,部分结果如图7所示。在无损情况下,由于是无损板结构系统与自身的递归,因此系统的相似程度最大,其CRP(图7(a))上出现了明显的斜对角线。随着弯曲次数的增加,损伤板的动力学特性与无损板间的差异性越来越大,导致图7(b)与图7(c)中的斜对角线小时,递归点逐渐减少且更加分散。
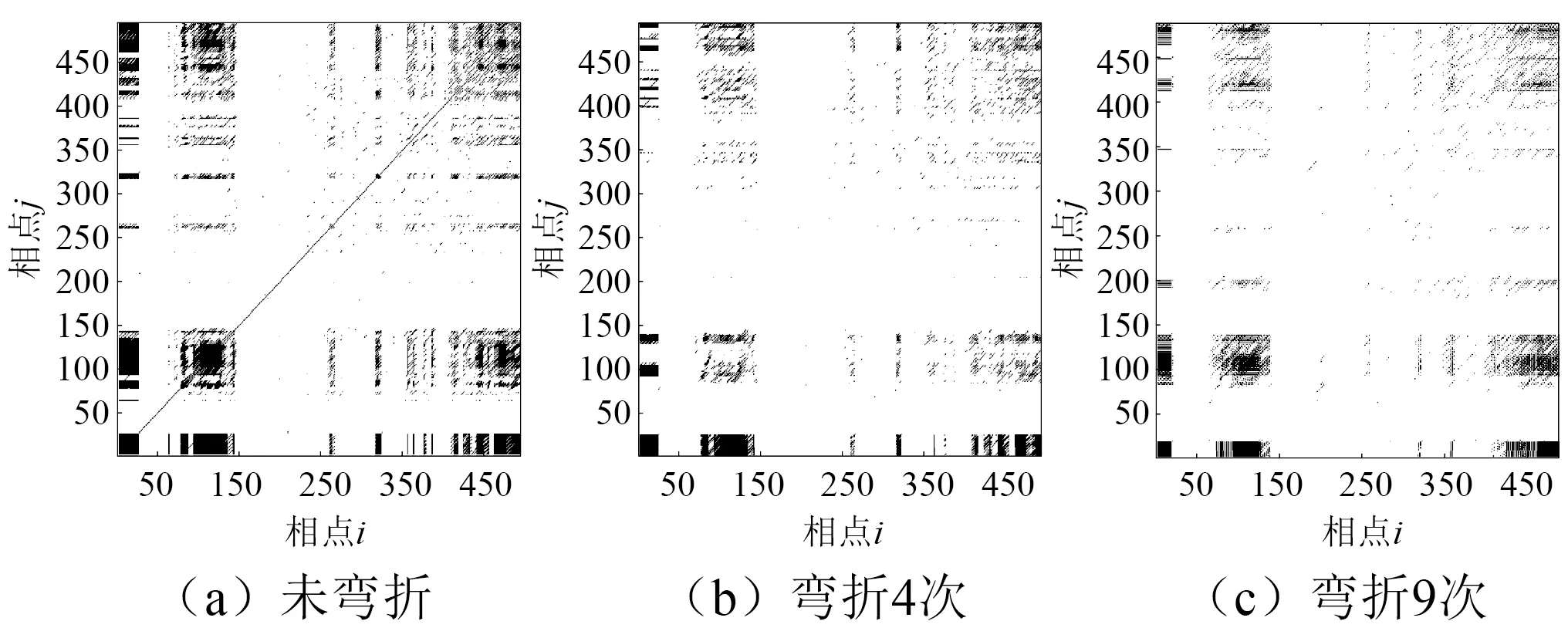
图7 试验信号CRP Fig.7 CRPs of test signals
3.3 损伤信号特征提取
为了对CRP特征进行量化描述,采用CRQA方法提取测试Lamb波信号的特征向量{RR,DET,LAM,RT1},结果如图8所示。可见,每个CRQA特征对弯折损伤的表征能力各异,且随着弯折次数变化波动幅度较大。这主要是因为,金属板弯折过程中产生的损伤类型与损伤分布各有不同,而不同的CRQA指数对不同损伤类型与其位置分布的敏感度与表征能力不同。尽管各个特征与弯折次数的线性相关性并不明显,但DET,RR与LAM基本随着弯折次数的增加呈现下降趋势,而RT1呈现上升趋势。
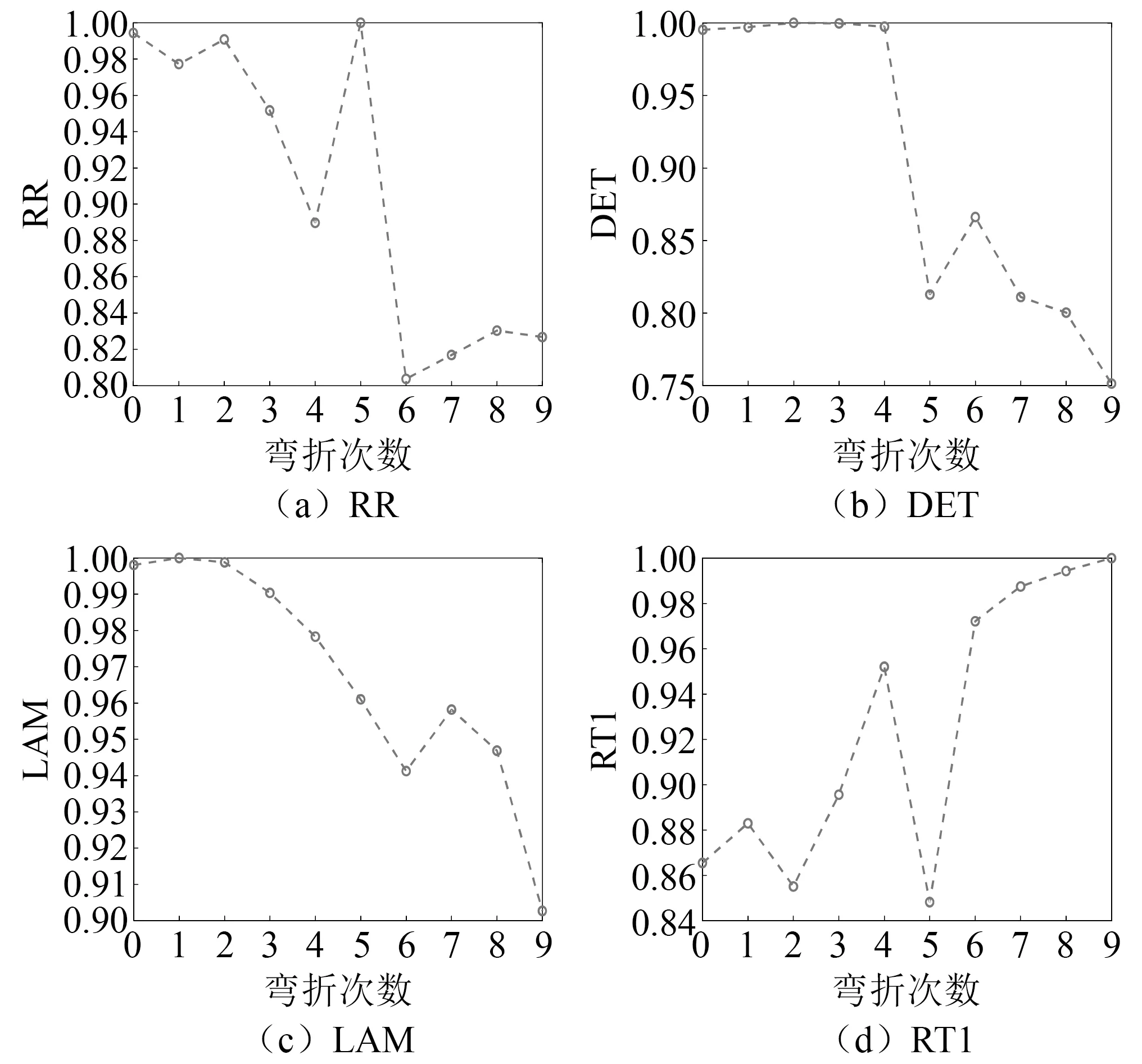
图8 试验信号CRQA特征Fig.8 CRQA features of test signals
3.4 损伤量化表征
为了对弯折铝板损伤进行一致性表征,采用10次同等测试条件下获得的无损信号的CRQA特征作为训练样本,建立SVDD模型,继而根据式(19)和式(20)计算各个弯折损伤信号的DI指数,结果如图9所示。图9也给出了β指数的变化曲线图可以看出,DI指数所拟合的曲线趋势更好。分别计算图9中两个指数拟合曲线的R-square与RMSE指数,结果如表2所示。从表2中可以看出,本文提出的DI指数与铝板弯折次数间具有更好的线性相关性。铝板弯折过程中,产生的损伤类型、长度,深度、个数、位置,方向、都无法用一个具体的参数进行描述,考虑这些因素的损伤程度参数难以建立,因此本文采用了疲劳弯曲次数来近似铝板实际损伤程度,DI指数与弯曲次数间较好的线性相关性验证了DI指数对铝板弯折损伤程度具有较好的量化表征能力。
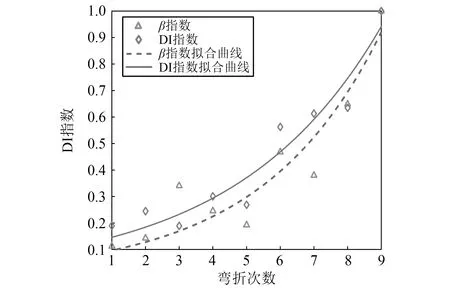
图9 试验板损伤指数 Fig.9 Damage indexes of experimental plate

表2 试验板损伤指数比较Tab.2 Comparison of damage indexes of experimental plate
4 结 论
针对金属板结构的疲劳损伤演变的非线性过程与超声导波信号的非线性特性,在损伤信号交叉递归分析的基础上建立了统一损伤指数并对金属板结构损伤进行了量化评估。论文的主要贡献在于:
(1)针对Lamb波的散射、透射、反射特性造成的损伤信号波形变化分析困难问题,引入了交叉递归分析方法从结构板的动力学特性角度进行了损伤信息的挖掘,并采用交叉递归图进行了损伤信息描述。
(2)针对金属板损伤程度难以量化的问题,采用了CRQA方法对损伤信号的CRP图进行了特征提取,并结合特征的单调性、相关性、鲁棒性及特征间的关联性对CRQA特征进行了优化选择。
(3)针对CRQA特征对金属板损伤表征能力的差异性,采用了SVDD模型对优化特征进行了融合,建立了能够对金属板损伤进行一致性表征的统一损伤指数。
论文采用了随机裂纹仿真模型与铝板弯折疲劳试验对本文提出的方法进行了验证分析。结果表明,本文提出的基于CRQA的统一损伤指数不仅能够对金属板疲劳裂纹损伤量化表征,而且具有较好的噪声鲁棒性,在板材疲劳损伤检测与健康评估方面具有较好的应用前景。
