爆炸载荷下加筋板的抗爆性能研究

2021-06-26琚泽宇苟瑞君张树海陈亚红郭永辉

弹箭与制导学报 2021年2期

琚泽宇，苟瑞君，张树海，陈亚红，李岩，郭永辉

(1 中北大学环境与安全工程学院，太原 030051；2 北京宇航系统工程研究院，北京 100076)

0 引言

布置加强筋是常见的金属板加固方式之一，通过布置合理的加强筋，可以很大程度上提高结构的力学性能，使其具有轻质、高比强度、高比刚度的特点，已被广泛应用在桥隧、车辆、舰船、武器等民用和军事领域。在爆炸冲击载荷作用下，加筋金属板受到几十、上百甚至上千MPa的压力，根据金属力学性能和结构抗爆性能的不同，加筋金属板产生弹性变形、塑性变形甚至破坏，进而导致设备整体功能的受损或失效。Balden等[1]利用AUTODYN分析软件，对金属圆薄板在局部爆炸载荷作用下的响应进行了研究，提出了爆炸载荷的锥形分布模型。Bonorchis等[2]利用AUTODYN分析软件，对平板在局部载荷作用下的响应进行了研究，提出了爆炸载荷的锥形分布模型和冲量分布拟合公式。王芳等[3]利用试验的手段，对金属平板在爆炸载荷下的塑性响应进行了研究，得出了在冲击波作用下考虑边界约束条件的金属方形靶板半经验挠度公式。侯海量等[4]通过MSC/DYTRAN有限元分析程序模拟了金属加筋板的动态响应和失效模式，得出了单根加筋的金属板的抗爆性能和加筋板质量与加强筋尺寸和布置方式的关系。甘露等[5]利用LS-DYNA分析软件，对在爆炸载荷下U形加筋板的动态响应和破坏模式进行了研究，得出在金属板上合理布置加强筋能有效降低金属板在爆炸载荷下破坏程度，减少残余变形。目前，关于金属加筋平板的爆炸响应研究大多集中于对平板的破快模式和挠度进行分析，而关于金属板不同加筋数量和加筋方式对金属板抗爆性能的影响鲜有公开报道[6-7]。

为了明确加强筋对金属板抗爆性能的影响，提高金属板整体力学性能，文中以铝合金板为研究对象，分析和研究不同加筋的铝合金板在不同爆炸载荷下的动力学响应，为金属板的抗爆设计提供了一定参考[8-10]。

1 模型建立及计算

1.1 模型建立及网格划分

根据研究对象的几何性质，在保证计算精度的前提下，为提高计算速度，建立1/4简化对称计算模型，如图1所示。其中金属方板边长为2L=400 mm，厚度c=6 mm，炸药布置于金属板中心正上方，爆炸高度D=200 mm。

图1 Model 2加强筋金属板计算结构图

基于ANSYS-WorkBench建立有限元几何模型，并对模型中的材料进行网格划分，金属板、加强筋、炸药的有限元模型均划分为八节点六面体网格，随后将模型导入AUTODYN,建立空气模型并对其进行网格划分，模型中TNT和空气均为Euler网格，金属板、加强筋均为Lagrange网格，爆炸冲击波和爆轰产物可在空气网格中自由流动，采用流固耦合算法。为提高计算精度，降低计算中由于网格负体积而导致计算不收敛的概率，在炸药中心和金属板中心连线周围区域设置细化网格。采用AUTODYN进行模型对称性和边界条件的设置。对金属板固支端施加固定边界条件，金属板、加强筋、炸药和空气域对称截面施加对称性速度边界条件，空气域自由端施加非反射边界条件。

选取工程中常见的8种金属板加筋类型，如图2所示，加强筋材料与金属板相同，长为200 mm,宽为6 mm,高为6 mm。模拟中设置4种TNT爆炸载荷药别为50 g，60 g，70 g和80 g。

图2 加强筋金属板模型示意图

1.2 材料模型

以TNT炸药为动力源，在AUTODYN中选取EOS_JWL状态方程描述其爆炸过程中爆轰产物体积和压力的关系，P-V关系式为:

(1)

式中：P为压强；V为炸药爆轰产物体积；ρ为炸药的密度；E为初始能量密度；A，B，R1，R2，ω为炸药特性参数。炸药特性参数的定义参考文献[11-13]，并由EXPLO5计算确定。

为了使计算结果和过程更加具有普遍参考性，在模拟中将空气材料用理想气体描述，单位质量空气压强Pg可表示为：

Pg=(γ-1)ρgeg

(2)

式中:空气密度ρg=0.001225 g/cm3；空气单位质量内能eg=206.8 kJ/g；绝热指数γ=1.4。

靶板选用8053-H116铝合金材料，材料本构参数如表1所示。

表1 5083-H116铝合金本构参数

材料模型采用大变形数值模拟中常用的Johnson-Cook模型，该模型可以较为准确的描述材料在爆炸冲击载荷下的变形，反应在高应变率情况下材料的应变硬化、应变率硬化、温度效应。等效应力σeq可表示为：

(3)

(4)

(5)

式中：Tr为参考温度298 K；Tm为材料熔点温度；T为材料环境温度。

他承担着西山农牧场阳光丽苑A区、B区、锦绣家园二期共20万平方米、大约60栋楼，1000多套住房的供暖维修服务任务。

1.3 网格尺寸的选择及有限元准确性验证

为进一步提高计算模拟的准确性，选择较为合适的网格尺寸很关键。首先对Model 0平板、60 g爆炸载荷进行验证性计算，设置空气计算网格尺寸为3 mm，局部细化网格为1 mm，渐变率为3，验证金属板分别选择网格尺寸为1 mm、1.5 mm、2 mm时，3种网格尺寸的计算精度，并与无孔平板中心点挠度的半经验公式[5]进行结果比较。无孔平板中心点挠度半经验公式表达式为：

(6)

式中：ω0为中心点挠度；we为装药质量；ρ为装药密度；L为方形平板边长一半；c为平板厚度；σs为平板屈服强度；ρt为平板密度；re为冲击波比冲量正反射系数i+为冲量常数；根据试验数据取：

(7)

式中：ΔP1为入射冲击波超压；ΔP2为反射冲击波超压；P0为标准大气压。

根据以上半经验公式计算所得，结合60 g爆炸载荷模拟计算数据如表2。

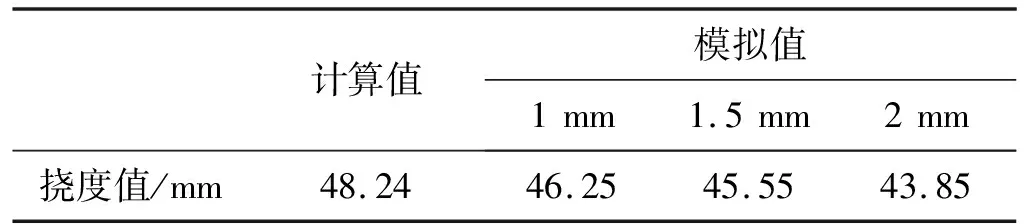
表2 经验计算结果与模拟结果

对比经验计算结果，金属板网格尺寸分别为1 mm，1.5 mm，2 mm时，挠度值误差分别为4.12%，5.57%，9.1%；网格尺寸为1 mm和1.5 mm的模拟结果相对误差为1.15%，网格尺寸为1.5 mm和3 mm的模拟结果相对误差为3.72%。以上结果说明，在兼顾计算模拟准确性和计算速度的情况下，选择网格尺寸为1.5 mm较为合适；从表中可看出，经验计算结果与模拟计算结果误差范围均低于10%，说明本研究所采用的计算模型合理，计算结果精度良好。

2 计算模拟结果及分析讨论

2.1 计算结果

图3为60 g TNT炸药，Model 1加筋金属板，起爆后冲击波及金属板响应压力云图。从金属板整体的爆炸冲击响应来看，整个响应过程可分为3个时间段[14]。0～60 μs为第一时间段，在此时间内，炸药起爆并瞬间产生高压冲击波，并以球面波的形式在空气中传播，逐渐向金属板逼近，在t=60 μs时冲击波最前端率先抵达面板中心，如图3(c)所示。60～160 μs为第二时间段，在此阶段内，冲击波最前端开始对金属板中心点进行加载，面板开始发生变形，进入弹性-塑性变形阶段，爆炸冲击波赋予金属板的能量以金属板的塑性变形能和动能的形式体现，如图4、图5所示，随着加载的进行金属板动能不断增大，并产生数倍于面板厚度的挠度变形。从160 μs之后为第三时间段，在此时间内，爆炸冲击波对金属板的加载作用停止，但是由于金属板自身惯性作用继续保持向下运动，如图4所示。由于金属板自身的阻尼作用，动能逐渐降低，一部分转化为金属板的塑性变形能，一部分转化为金属板的弹性势能，t=640 μs时金属板的动能第一次全部转化为弹性势能，金属板中心达到最大峰值挠度，之后金属板进入自由振动阶段。由于金属板是弹塑性材料，随着弹性变形能的释放，金属板动能增加，表现为金属板的回弹，如图5所示，出现了与冲击波加载方向相反的速度，金属板中心出现围绕固定塑性挠度值的震荡[15]，金属板出现动能和弹性势能之间的能量转换，并以热能作为能量损失，当弹性势能完全卸载全局静止后，最终残余挠度值低于峰值挠度。根据曲线形貌，通过求取曲线中弹性振动阶段多个振动数据的波峰波谷挠度平均值，可以较好预测全局静止后金属板的塑性挠度。

图3 60 g TNT、Model 1加筋板响应过程及爆炸演化图

图4 60 g TNT、Model 1加筋板中心点位移、速度时程曲线

2.2 挠度分析

图5 不同比例距离、不同类型金属板中心点残余挠度曲线

由图5可知，在所有模拟工况下，不同加筋类型金属板虽均出现不同程度的凹陷。以金属板中心点残余挠度为研究目标，以比例距离为参考变量，可以看出，随着比例距离的减小(爆炸载荷的增加)，从Model 0至Model 4-1所有板型的残余挠度值均逐渐增加，从残余挠度值发展趋势可以看出，金属板中心残余挠度值大小和比例距离基本呈线性关系，且Model 0型的线性贴合程度最好，Model 2-1,Model 3-1,Model 4-1型线性贴合程度次之，而其他类型加筋金属板中心点残余挠度随爆炸载荷的变化，在线性关系的基础上，还存在随着比例距离的减小，金属板中心点残余挠度有轻微上扬趋势。因为一方面，爆炸冲击波是以球面波的形式在空气中传播，在小于金属板面积的区域内作用于金属板时，金属板直接受载荷区域为圆形平面；另一方面，对金属板布置加强筋，使原本具有各向同性力学性质的金属板，成为在不同位置、不同方向上受力反应不同的各向异性材料；而在圆形受载荷面上，无加筋金属板具有过几何中心的完全对称性，Model 2-1，Model 3-1,Model 4-1型加筋板，在过金属板几何中心连线的对称性上，也优于单方向加筋板，所以在受爆炸冲击载荷时，金属板在产生膜力效应的对称性上，Model 0型加筋板最高，Model 2-1，Model 3-1，Model 4-1型加筋板次之，其他类型加筋板最差，进而在计算模拟中表现出，爆炸载荷与金属板中心残余挠度值的线性关系贴合程度上，Model 0型加筋板>Model 2-1,Model 3-1,Model 4-1型加筋板>其他类型加筋板；并且通过分析平行设置加强筋模型的挠度变化，可以看出，对于平行设置的加强筋，随着加筋数量的增加，载荷与挠度值线性关系贴合程度有所提高。从总体发展趋势来看，在达到金属板出现破口载荷之前，金属板中心点残余挠度值大小和载荷值基本呈线性关系。

如图6所示，以金属板中心点残余挠度为研究目标，以加筋板类型为参考变量，在确定的爆炸载荷下，金属板中心点残余挠度，随着金属板加筋数量的增加逐渐降低，从图中可以看出，由于加筋类型的改变，中心点残余挠度下降呈类似“阶梯式”变化，只考虑增加加强筋的数量，金属板中心点残余挠度值的减少量并不明显，加强筋数量从0增加至4，爆炸载荷50～80 g，残余挠度分别相对降低了1.5%，0.768%，2.463%，1.056%；1.17%，0.67%，1.088%，0.794%；2.17%，1.051%，0.525%，0.323%；1.48%，0.28%，0.383%，1.907%；可以看出加强筋布置数量越多，金属板中心点残余挠度减少量的衰减越明显。相同数量但不同加筋布置方式使金属板中心点残余挠度存在突跃变化，爆炸载荷50～80 g，Model 2-1比Model 2挠度降低了2.93%，1.90%，1.84%，1.62%；Model 3-1比Model 3挠度降低了7.043%,5.99%,3.85%,4.647%；Model 4-1比Model 4挠度降低了0.36%，1.83%，0.233%，0.773%。并且从图中可以看出，改变金属板的加筋方式Model 3-1型中心点残余挠度表现最优秀，Model 4-1型中心残余挠度较大。这是因为，在该种加筋方式下，加强筋将金属板中心区域分割成一个独立的，类似四周固支的小块金属板，在爆炸载荷下，球面冲击波首先接触金属板中心，冲击波作用下中心点残余挠度较大，从2.3节能量的分析可以看出，Model 4-1型加筋偏向与对金属板整体的加固作用。可以得出，交叉十字型加筋方式比平行加筋有更好的中心点残余挠度表现，并且可以预测，加筋方式的改变可使金属板通过少量加筋，达到更好的抗爆效果。

图6 不同载荷、不同类型金属板中心点残余挠度分布

2.3 能量分析

通过在计算模型中布置监测点，观察和分析监测点记录的能量数据可以看出：当爆炸冲击波作用于金属板时，爆炸冲击波作用于金属板的能量大部分以塑性变形的方式体现，其他一部分能量转变为金属板的动能和热能，由于热能的传递需要较长的时间尺度，远超过爆炸过程中金属板的响应时间，所以可以近似认为，爆炸冲击波作用于金属板的能量全部转化为金属板的塑性变形能和动能。金属板从爆炸冲击波中获取的能量E1(以下简称总能量)和塑性变形能E2计算结果值如表3所示。

表3 不同爆炸载荷下不同类型金属板的总能量和塑性变形能单位：J

从表3可以看出，在相同爆炸载荷下，随着不同类型金属板加强筋数量的增加，E1，E2总体均呈降低趋势，因为加强筋的存在提高了金属板的相对刚度，冲击波作用于金属板时，较大的刚度使金属板具有较强的抵抗变形的能力。能量排序依次为：Model 0>Model 1>Model 2>Model 2-1>Model 3>Model 4>Model 4-1>Model 3-1，Model 4-1处于Model 4和Model 3-1之间，而Model 3-1型总能量值最小。这是因为，一方面爆炸冲击波在空气中是以球面波的形式传播，作用于金属板的初始位置位于金属板的中心点，而Model 4-1型金属板中心点并没有布置加强筋，在高应变率下，致使金属板在中心方形区域产生较大的挠度，另一方面随着加载的进行，爆炸冲击波在金属板中形成的应力波传递至加强筋位置，加强筋的加固作用开始体现，由于加强筋的布置仍具有一定的数量和形式优势，所以金属板除中心点外整体的塑性变形并不大，E1和E2值仍较小。而Model 3-1型金属板中心点布置有加强筋，在冲击波与金属板初始接触时，加强筋的存在，使金属板中心点具备更强抵抗变形的能力，联合加筋数量和十字交叉加筋方式的优势，金属板表现出E1和E2值最小的情况。表明当爆炸载荷不能等效为均布载荷时，需考虑冲击波与进金属板初始接触位置的强度，将加强筋穿过炸药中心点在金属板处的投影，能有效降低金属板在爆炸载荷下的中心点残余挠度。

通过联合分析每种爆炸载荷下的总能量和塑性变形能，可以看出，随着加强筋数量和方式的改变，塑性变形能在总能量中的占比逐渐降低，以50 g爆炸载荷为例，从Model 0至Model 4-1，塑性变形能分别占总能量的92%，90.5%，89.1%，87.9%，86%，85.2%，84%，83.5%。表明在同样的爆炸载荷下，随着加强筋数量的增加和方式的改变，虽然局部变形存在差异，但金属板的整体变形逐渐降低，整体抗爆性能逐渐提高。

分析对比50～80 g不同爆炸载荷下，金属板的塑性变形能曲线和总能量曲线可以看出，随着爆炸载荷的增加，曲线之间的分布距离逐渐缩短，说明随着爆炸载荷的增加，金属板结构本身对金属板在爆炸载荷中获取的能量大小的影响逐渐降低，加强筋对金属板的加强作用逐渐减弱，载荷大小成为影响金属板能量获取的主导因素。