某风扇增压级行波共振故障机理研究

马会防，张 辉，吴志青，王卫国，高修磊

(中国航发商用航空发动机有限责任公司，上海 200241)

在航空发动机、汽轮机等旋转机械中，广泛使用了薄壁圆柱壳结构，对这类结构进行振动特性、故障诊断技术研究，具有重要的工程应用和参考价值。

计算研究方面，王宇等[1-4]利用传递矩阵等方法研究了旋转薄壁圆柱壳的行波共振特性，包括不同材质的涂层、不同的边界条件等对行波共振特性的影响。李文达等[5]基于Sanders壳体理论，采用波传播方法和傅里叶级数展开法，研究了弹性约束边界条件下旋转薄壁圆柱壳的振动特性。韩清凯等[6]利用传递矩阵法研究了旋转薄壁圆柱壳及带有篦齿结构时的固有频率特性。

试验测试方面，何刘海等[7-9]利用声波导管测量了航空发动机附件齿轮的行波共振噪声，对行波共振频率、共振转速及节径振动声辐射量级进行了分析，研究表明被测锥齿轮在运行转速范围内存在多个节径行波共振,最大分频动应力在五节径后行波处。

振动故障诊断方面，工程中关于行波共振诊断的研究则报道很少，王海霞等[10]针对典型的发动机附件机匣振动超限情况,确定了固有频率共振是引起发附件机匣振动超限的主要原因，在振动支架上安装辅助重物以改变系统固有频率可避免固有频率共振，另外还调整了发动机附件机匣安装状态,降低了基础振动水平。郑旭东等[11]介绍了甩油孔位置不当引发的自激振动故障，经试验验证，排故措施有效。柏树生等[12]介绍了整机振动常见故障及其排除措施，故障类型包括转子不平衡、转子热弯曲、转子不对中、转子碰摩、滚动轴承故障、齿轮故障、油膜振荡等十余种故障，但不包含行波共振。

本文介绍了某风扇增压级的一次振动故障，通过分析推测故障机理为试验件发生了行波共振，并根据故障机理制定了整改措施，经试验验证，措施有效。

1 故障简介

1.1 风扇增压级结构及振动测点

风扇增压级试验件由1级风扇、3级增压级构成，具体如图1所示。

1.风扇叶片；2.风扇盘；3.风扇轴；4.增压级鼓筒；5.增压级一级动叶；6.增压级二级动叶；7.增压级三级动叶；8.支点轴承包括滚棒轴承；9.滚珠轴承；10.静子件包括增压级零级静叶及其固定机匣；11.增压级一级静叶及其固定机匣；12.增压级二级静叶及其固定机匣；13.增压级三级静叶及其固定机匣；14.风扇机匣；15.一级静叶固定螺栓组；16.二级静叶固定螺栓组；17.三级静叶固定螺栓组；18.前承力机匣；19.滚珠轴承安装边；20.滚棒轴承安装边。图1 试验件结构示意图Fig.1 Sketch for structure of the test fig

振动测点位于滚珠轴承安装边、滚棒轴承安装边处，两个轴承支点都在水平、垂直方向上布置了加速度传感器，即共有4个径向振动测点。

该试验件为气动性能试验件，安装于试验台架上，各级动叶前后均布置了气动参数(静压、动压)测量传感器，用测量气动性能。

1.2 故障现象

试验由3 700 r/min向4 100 r/min升转过程中，转速达到3 960 r/min时，滚棒轴承座垂直方向基频振动(对应于转速1倍频的振动)由9 mm/s突然飙升至20 mm/s，之后很快降低至12 mm/s左右，但仍超过振动限制值11 mm/s，随后降转至3 700 r/min，请参考如图2所示的振动与转速曲线，降转后振动比之前同转速下明显变大，随后降转、停止了试验。

针对振动超限的时段，查对气动参数的测量结果，未发现突变等明显的异常现象；振动故障时的试验件压比较低，总压比不大于2.0，气动能量较小。

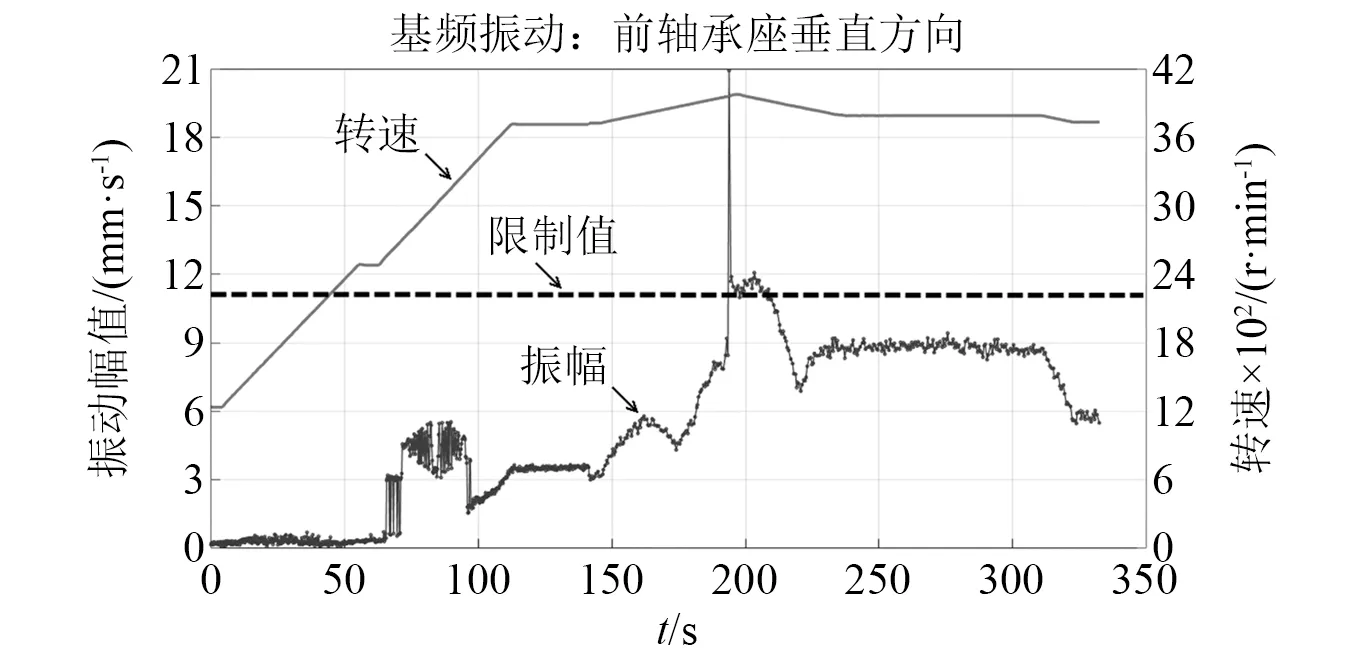
图2 振动与转速时域图Fig.2 Time field curves of vibration and rotating speed

试验后的故检发现主要有5处异常情况，其分布如图3所示。

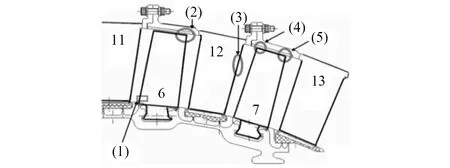
图3 异常情况分布示意图Fig.3 Sketch for distribution of abnormal situations

图3中：(1)处的圆周向连续7片二级动叶根部出现裂纹，裂纹如图4(a)所示；(2)处的圆周向连续7片二级动叶顶部出现折弯，如图4(b)所示，折弯叶片与裂纹叶片为同一区域的叶片；(3)处有连续的二级静叶出现折弯，如4(c)所示；(4)与(5)处的三级动叶顶部出现缺失、磨损，如图4(d)所示。

图4 损伤图片Fig.4 Pictures of damages

试验件分解时发现的故障信息包括：①螺栓松动；②二级静叶损伤的整圈分布情况；③三级动叶对应机匣涂层的损伤及其整圈分布情况。

螺栓组16出现明显的松动，该组螺栓一共30个，拧紧力矩约为12 N·m，分解力矩6～12 N·m，部分螺栓的分解力矩和拧紧力矩相差较大，且有一定的分布规律，如图5所示。

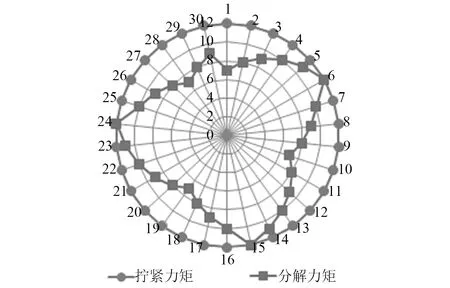
图5 螺栓组的拧紧力矩和分解力矩Fig.5 Sketch for tightening and loosening moment of a set of bolts

二级静叶损伤分布及局部放大图，如图6所示。

三级动叶对应机匣上涂层的损伤情况及局部放大图，如图7所示。

图7 三级动叶对应机匣上涂层的损伤分布及局部放大图Fig.7 Pictures for damage distribution and partial enlargement of the coating on the case corresponding to the third stage blade

2 故障特征分析

2.1 基于能量法对转速信号进行分析

振动飙升发生在升转过程中，根据故检查结果，振动飙升时发生了转静子碰磨、碰撞，碰撞消耗转子的旋转能量，应该会引起转速升速率下降，甚至是转速下降，因此将转速与振动信号放在同一时间轴上进行时序对比，查看碰撞后转速变化情况。

转速的原始信号是脉冲信号，对脉冲信号记数以计算出转速，采用多少个脉冲数进行一次转速计算比较关键，脉冲数太多，可能导致计算出的转速对转速变化不敏感，即实际的转速波动不能被发现。本文采用较少的脉冲数进行转速计算，将算出的转速与振动信号表达在同一张图上，横轴为时间，结果如图8所示。

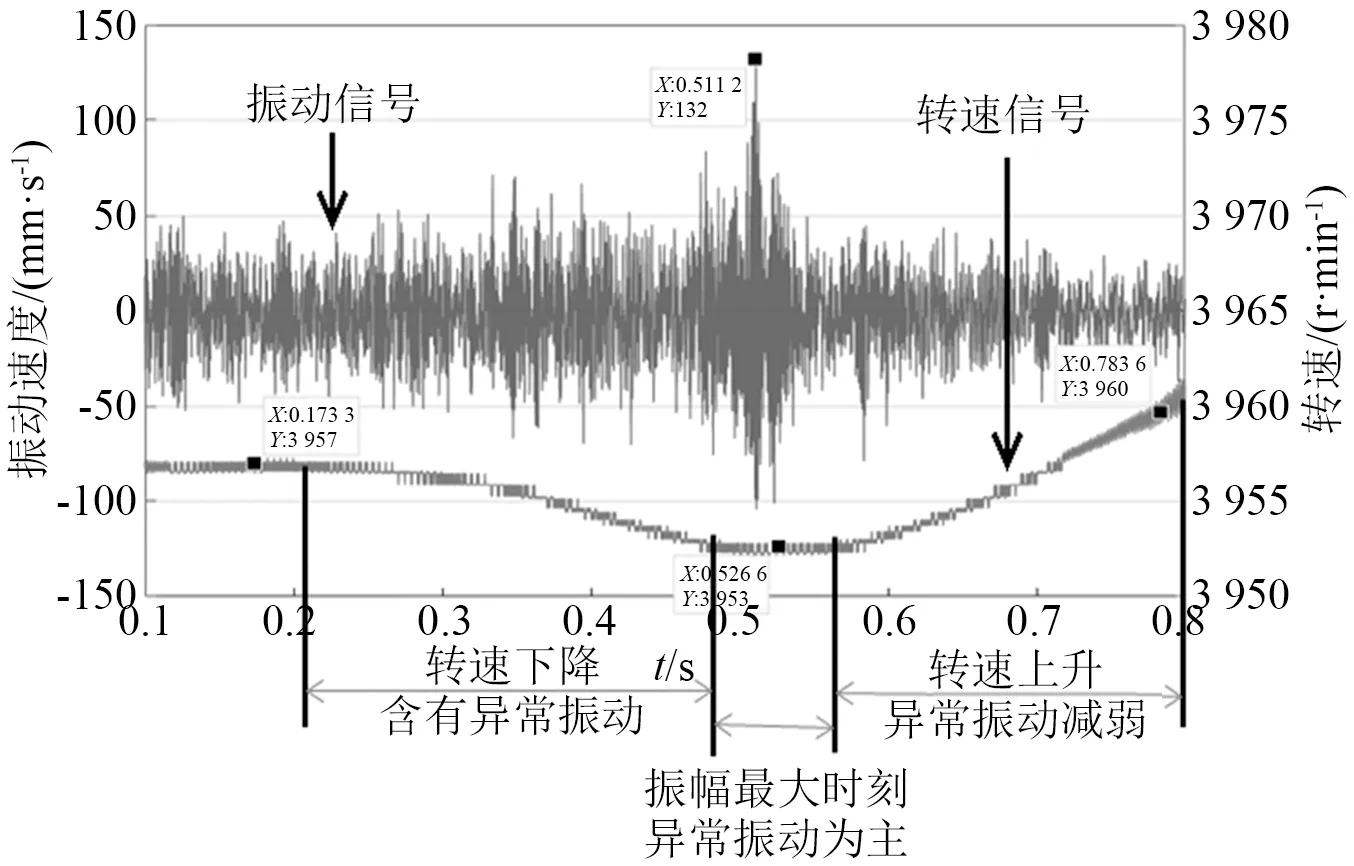
图8 碰撞时振动与转速信号对比图Fig.8 Sketch for comparison of vibration and rotating speed at impact time

振动信号中幅值最大的时刻为碰撞时刻，奇怪的是碰撞前转速就在下降了，却在碰撞之后恢复了上升趋势。

根据这一不寻常的现象，提出如下推测：①转速下降段的振动信号内含有异常振动，或者说异常振动导致转速下降；②振幅最大时段(转速处于平直段)，振动中的异常振动能量达到最大，即异常振动导致了振动幅值飙升；③碰撞后的转速上升段，异常振动减弱、或者已经消失，即异常振动的减弱、消失不再耗费转子的旋转能量，使得转速恢复了上升趋势。

根据推测，将振动信号依据转速的变化分为了3段(见图8)：①转速下降段，简称“碰撞前”；②振幅最大时段，即转速平直段，简称“碰撞时”，这一段时长约0.15 s；③转速上升段，简称“碰撞后”。对分别对3个时段的振动信号进行频谱分析，以期发现异常振动的振动频率。

2.2 基于振动信号分析推断异常振动频率

图9是200 s时长、500 Hz范围内的快速傅里叶变换(fast fourier transform，FFT)瀑布图，图9上坐标轴时间约40 s时发生了碰撞。测试系统中一直存在明显的工频50 Hz及其倍频250 Hz，350 Hz等干扰信号(试验现场曾尝试排除干扰，但没有奏效)，在频谱分析中需要忽略这些干扰信号。

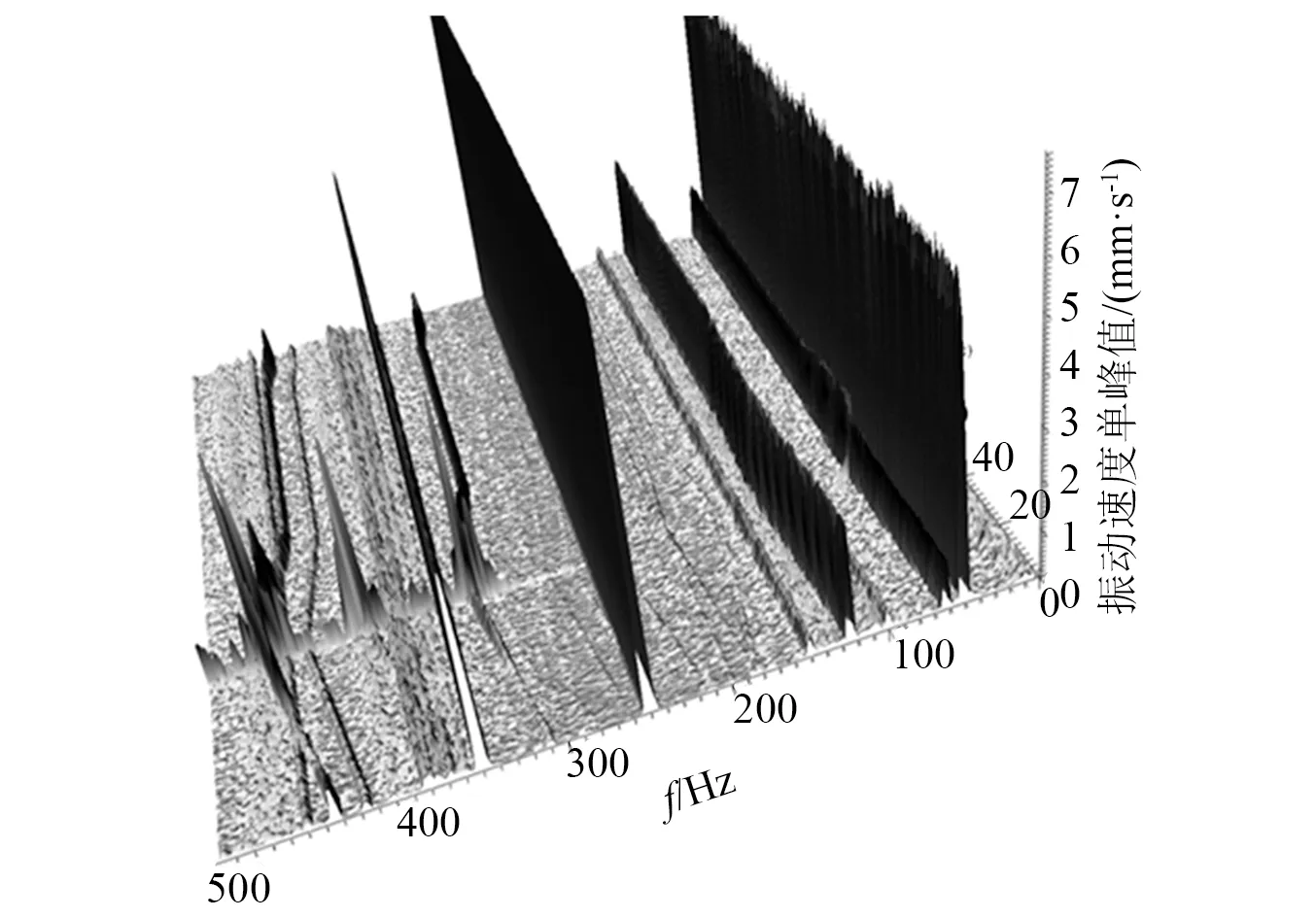
图9 测试系统中的干扰信号成分Fig.9 Undesired signal components in the testing system

碰撞时刻的短暂信号为非稳态信号，本文先采用小波分析方法对图8中的振动信号进行分析，结果如图10所示：①小波分析结果中也有明显的50 Hz，250 Hz等干扰信号，与图9中的结果相吻合；②与转速相应的基频振动信号带振幅较大，信号带比较明显，易于辨识，在图10坐标轴时间约0.7 s时发生碰撞，碰撞时基频振幅明显增大，约16～18 mm/s，与图2中的试验现场监测数据相接近；③300多 Hz的振动(疑似异常振动)振幅明显，碰撞时振幅较大(约20 mm/s)，且在碰撞前也有较大幅值，这说明碰撞前就存在刮磨，与图8中“碰撞前转速下降”相吻合。

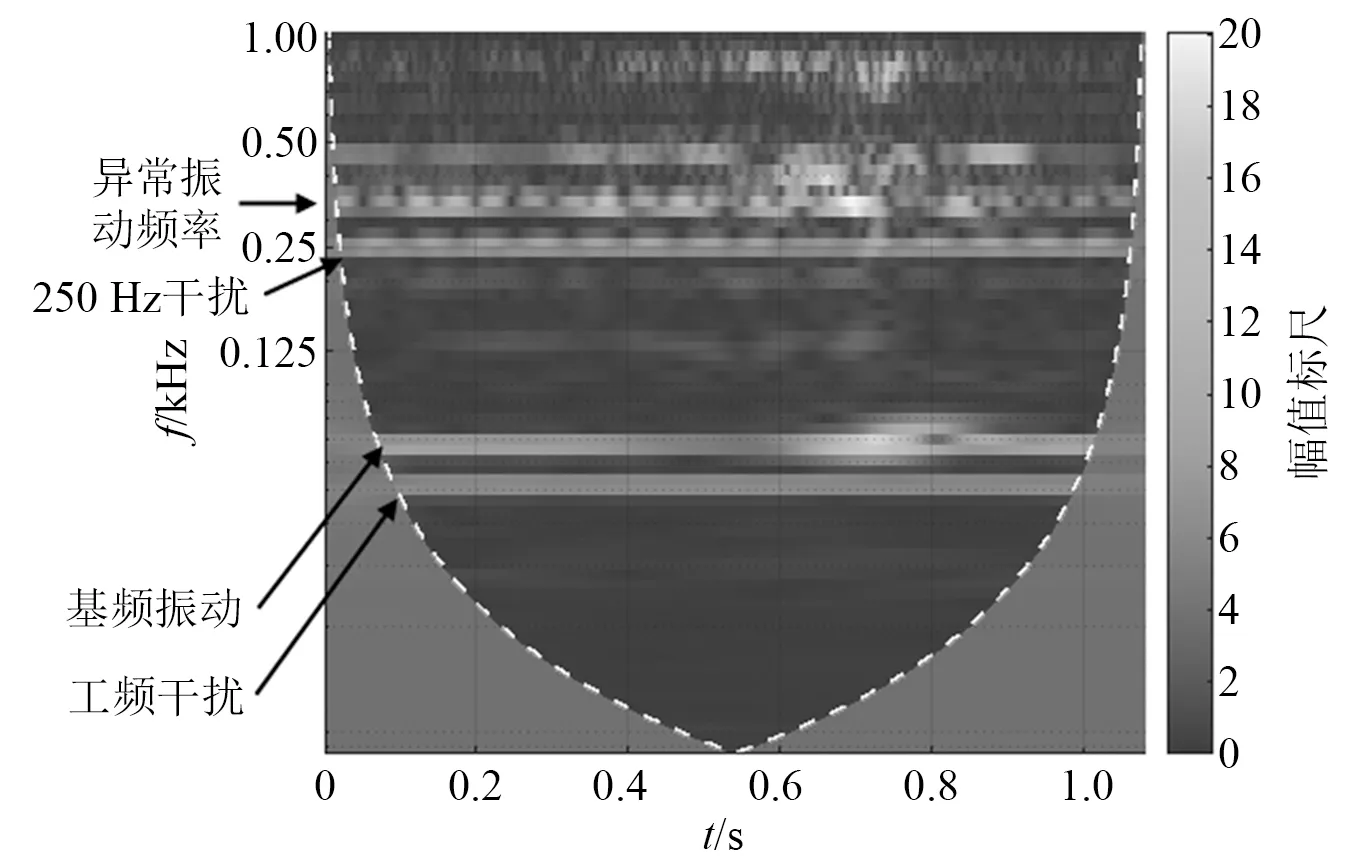
图10 小波分析结果Fig.10 Wavelet analysis result

对图8中的3段振动信号还进行了FFT分析，结果如图11所示，结果显示：330 Hz处的振动频率在碰撞前约3.5 mm/s，碰撞后降低到约2 mm/s，变化明显，碰撞时除了基频之外，325 Hz处的振幅达到最大，考虑到碰撞时段频域分辨率较低，结合碰撞前后的频率，325 Hz振幅较大应该是330 Hz处能量增大的表现。

图11 3段振动信号的频谱对比Fig.11 Spectrum comparison of three pieces of vibration signal

通过上述对振动信号的小波分析、FFT分析，我们可以推测异常振动故障频率约为330 Hz。

2.3 基于磨痕特征推断振型

图7所示的机匣涂层出现严重刮磨、掉块的区域在圆周向有明显的周期性，用黑色区域表示严重刮磨区域，上呈现类似于3节径振型的分布规律，如图12所示。

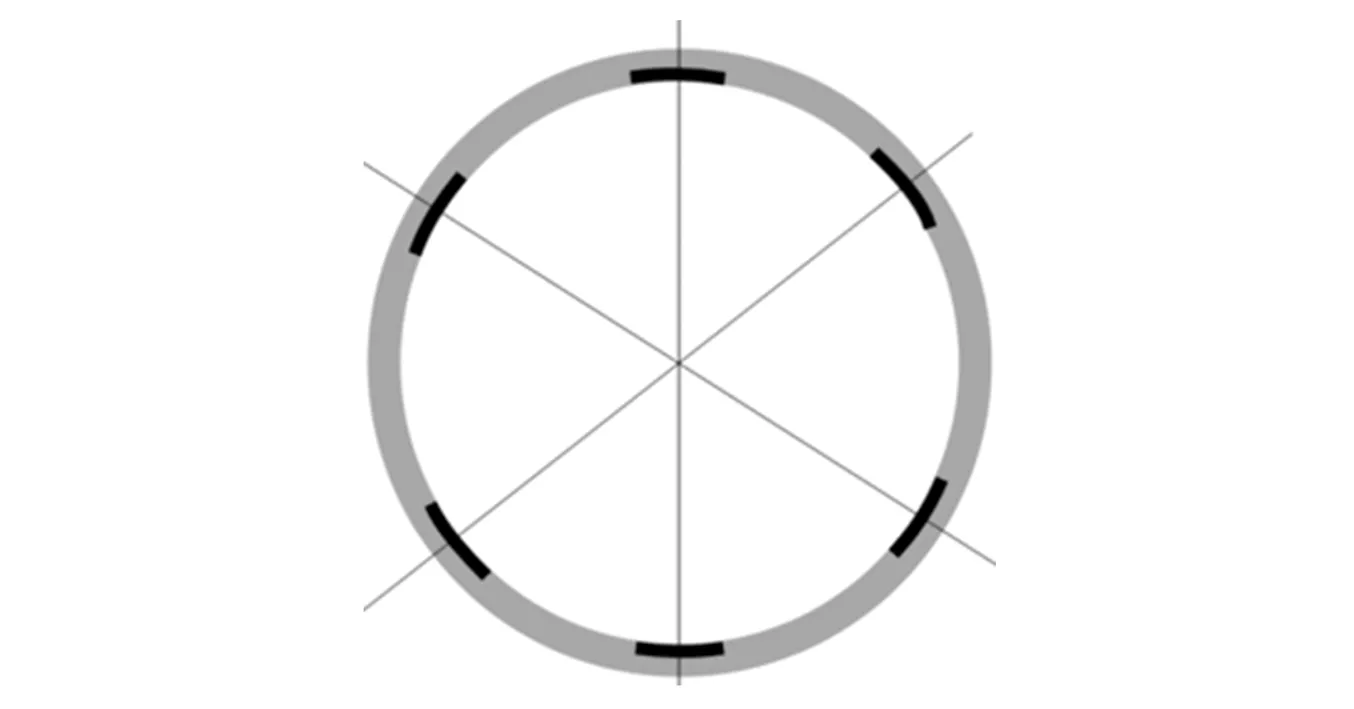
图12 涂层碰磨严重区域分布规律示意图Fig.12 Sketch for distribution law of coating damaged seriously

二级静叶变形也呈现明显的规律性，二级静叶共有111片，有变形的用带有底色的圆弧段表示，没有变形的白色的圆弧段表示，圆弧段上的数字表示该区域内的静叶个数，则图6中的叶片损伤情况呈现类似于3节径振型的分布规律，如图13所示。

根据静叶损伤规律、机匣涂层磨痕规律，结合螺栓松动规律，可以推测异常振动期间发生了严重的3节径振型，但不确定哪个部件的3节径振动，有以下3种可能：①转子鼓筒的3节径振动；②静子机匣的3节径振动；③转子鼓筒、静子机匣都发生了3节径振动。

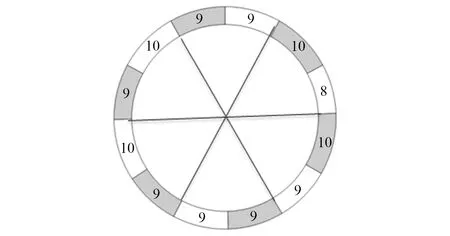
图13 二级静叶损伤分布规律示意图Fig.13 Sketch for damage distribution law of the second stator blades

2.4 轴心轨迹分析

2.2节介绍了振动信号中的干扰信号，本文根据专利技术[13]设计了多带阻滤波器，可过滤多组干扰信号，将过滤后的时域速度信号再积分成位移信号，得到图8中三段信号的轴心轨迹，轨迹如图14所示。

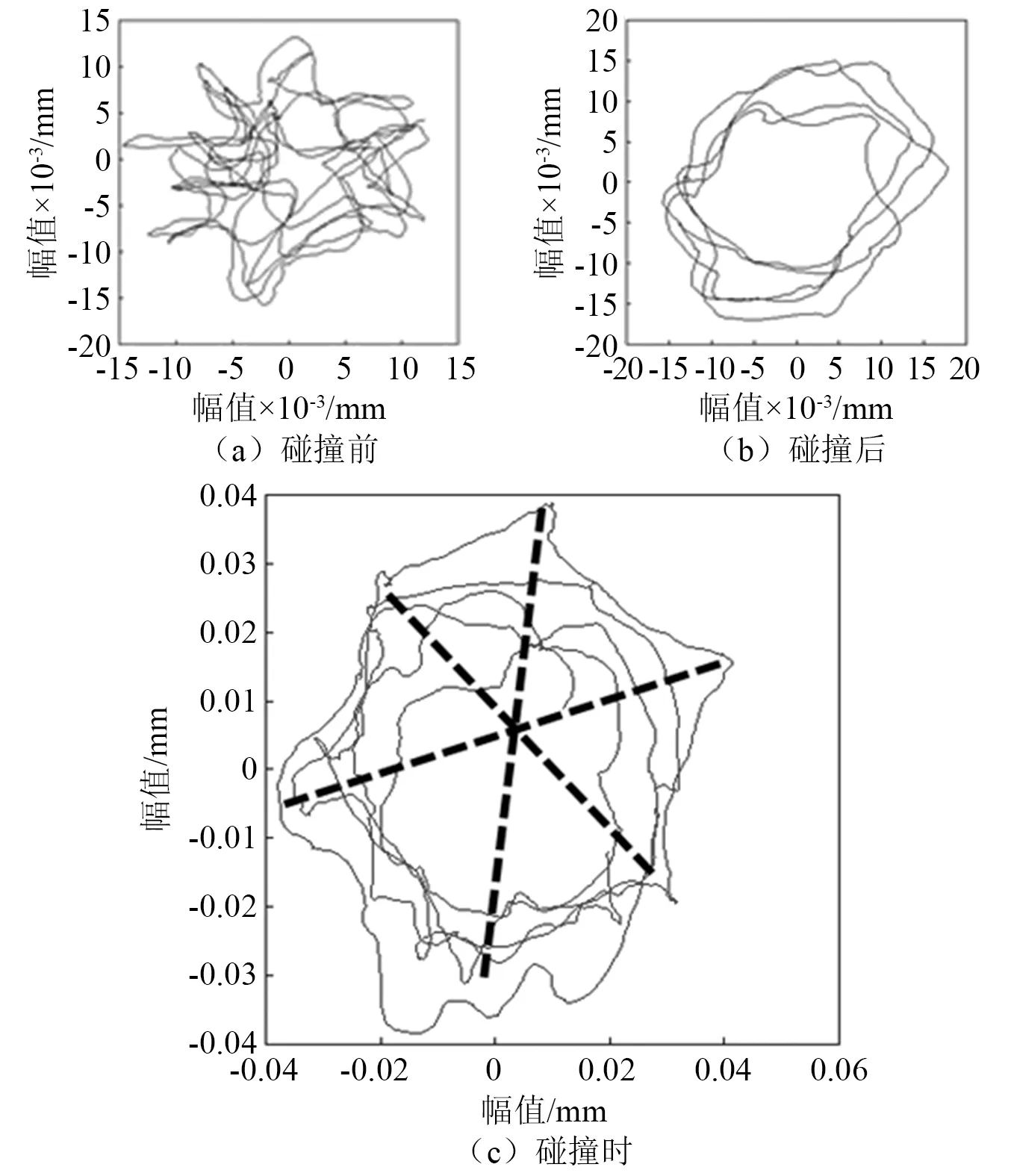
图14 滚棒轴承支点处的轴心轨迹Fig.14 Sketch for orbit at rod rolling bearing

图14中的3张轨迹图坐标轴比例尺一致，“碰撞前”的轴心轨迹有明显的“突尖”，显示转子可能已经处于不稳定的碰磨状态，但振幅较小，不到0.02 mm；“碰撞时”的轴心轨迹明显变大，约增大1倍，达到0.04 mm，且大致呈现六边形；“碰撞后”振幅恢复到“碰撞前”的水平，基本成圆形，处于比较稳定的状态。

根据轴心轨迹分析结果，可推测碰撞前已经发生了碰磨，与小波分析结果相吻合；碰撞时转子上也存在明显的3节径振型，与涂层磨痕分析结果可互相支撑。

2.5 静子机匣模态试验

在图1所示螺栓组15左侧2 cm处的零级静叶机匣上布置一圈测点(a圈测点)，螺栓组16右侧2 cm处的二级静叶机匣上布置一圈测点(b圈测点)，在螺栓组17处的三级静叶机匣法兰边上布置一圈测点(c圈测点)，共3圈测点，每圈圆周上布置24个测点。为模拟螺栓松动对模态的影响，3组螺栓拧紧前、拧紧后分别做了一次模态试验，两次试验的3节径振型类似，a圈变形相对较大、c圈变形相对较小，如图15所示，拧紧前模态频率129 Hz，拧紧后模态频率134 Hz。

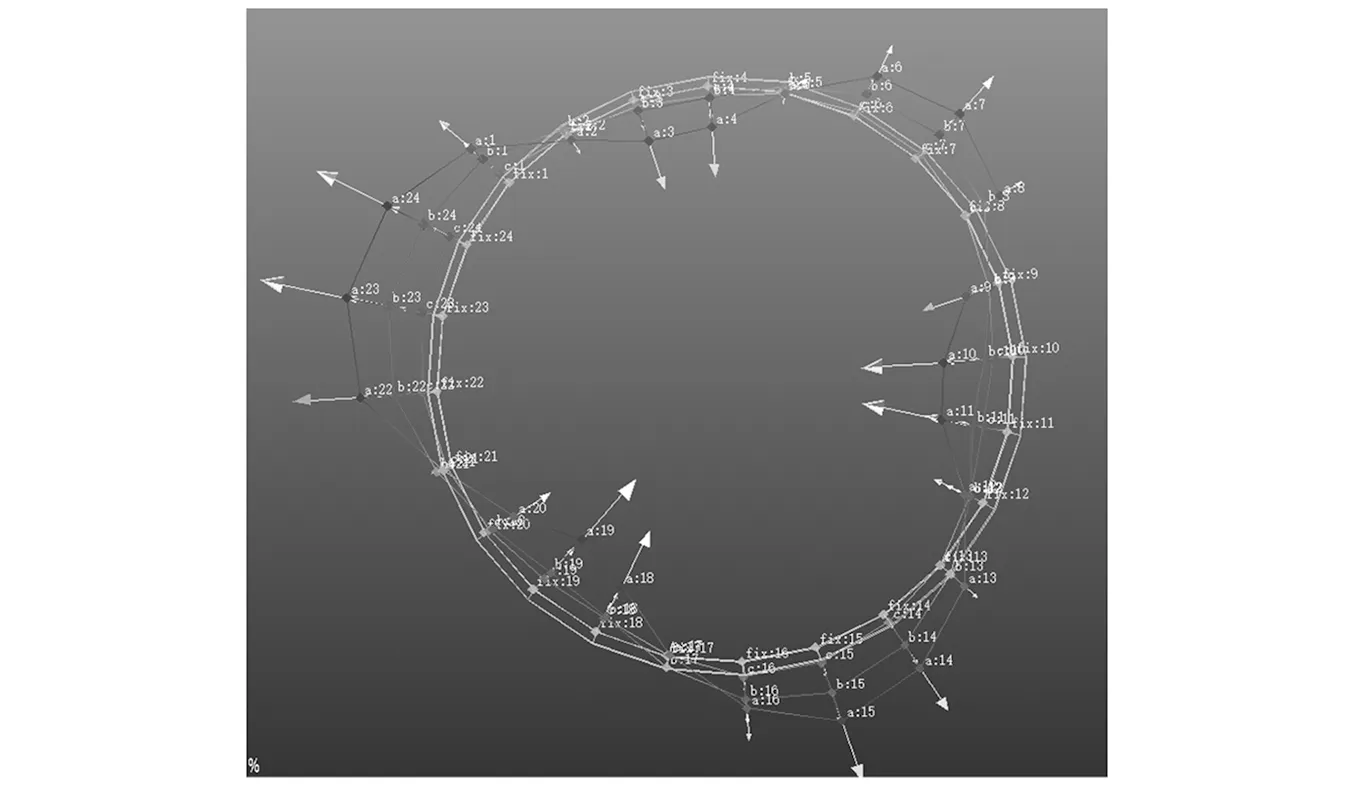
图15 机匣模态试验结果Fig.15 Result of case modal experiment

根据机匣模态试验结果，机匣3节径振型频率129～134 Hz，与异常振动频率相差很大，机匣发生3节径共振的可能性相对较小。

2.6 转子鼓筒模态分析

转子鼓筒由于受旋转的影响，在固定坐标系下观察其3节径振型的频率是转速的函数，相对静子机匣的后行波频率f计算公式为

f=fm-mN

(1)

式中：fm为节径数为m的动频，Hz；N为转子旋转频率，Hz。

根据式(1)以及转子鼓筒的3节径模态分析结果，其相对静子机匣的后行波频率如图16所示。

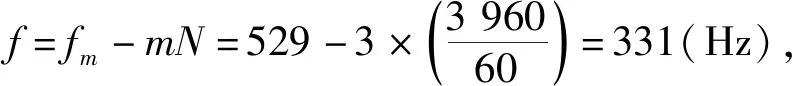
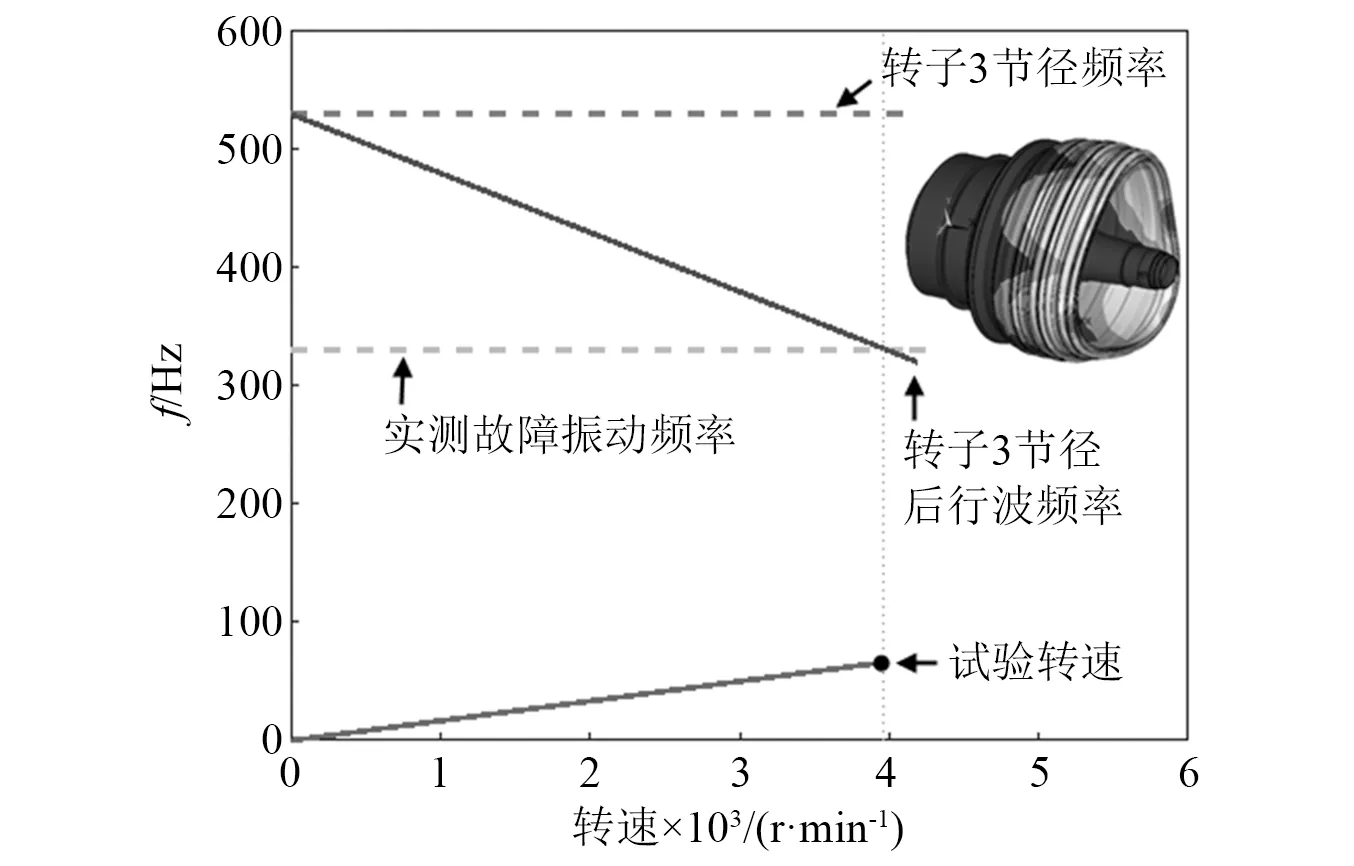
图16 转子鼓筒模态分析结果Fig.16 Result of rotor drum modal analysis

2.7 综合分析结果，提出故障机理

本文思路如图17所示，以转速分析、涂层磨痕分析为切入点，进而完成了振动信号小波分析分析、轴心轨迹分析等，以及机匣模态试验、转子鼓筒模态分析，综合各分析结果结果，提出如下故障机理：①转子升转过程中发生碰磨，碰磨导致转子鼓筒3节径后行波共振，共振导致振幅突增，产生严重碰磨、碰撞冲击；②碰撞时二级动叶、三级动叶与对应机匣严重碰磨，特别是三级动叶，与机匣碰撞后叶身变形较大，与二级静叶也发生碰撞；③转静子碰撞后，转静子之间的间隙增大，摩擦情况缓解，摩擦导致的共振现象消失，振动恢复至相对较低、但仍然超限的水平。

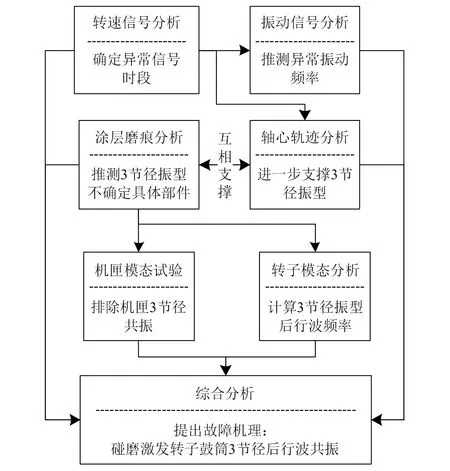
图17 振动故障分析思路图Fig.17 Vibration fault analysis map

3 故障机理的验证

基于故障机理，针对故障发生的条件制定了2项整改措施：①增加转静子之间的间隙，使试验转速内不发生剐蹭、碰磨；②增加机匣之间连接螺栓的个数，并采用防松措施，避免螺栓松动，导致机匣连接不牢而引起转静子碰磨。

针对测试中的干扰信号，更换了传感器的屏蔽线，更换了信号采集与分析测试系统。

完成整改后，试验件顺利实现全转速运转，转速达到4 222 r/min，测点振动以1倍转速对应的基频振动为主，干扰信号消失，如图18所示。振动故障没有再次出现，证明排故措施有效；有效的排故措施进一步证明振动故障分析过程比较合理，振动故障模式具有较强的合理性、真实性。

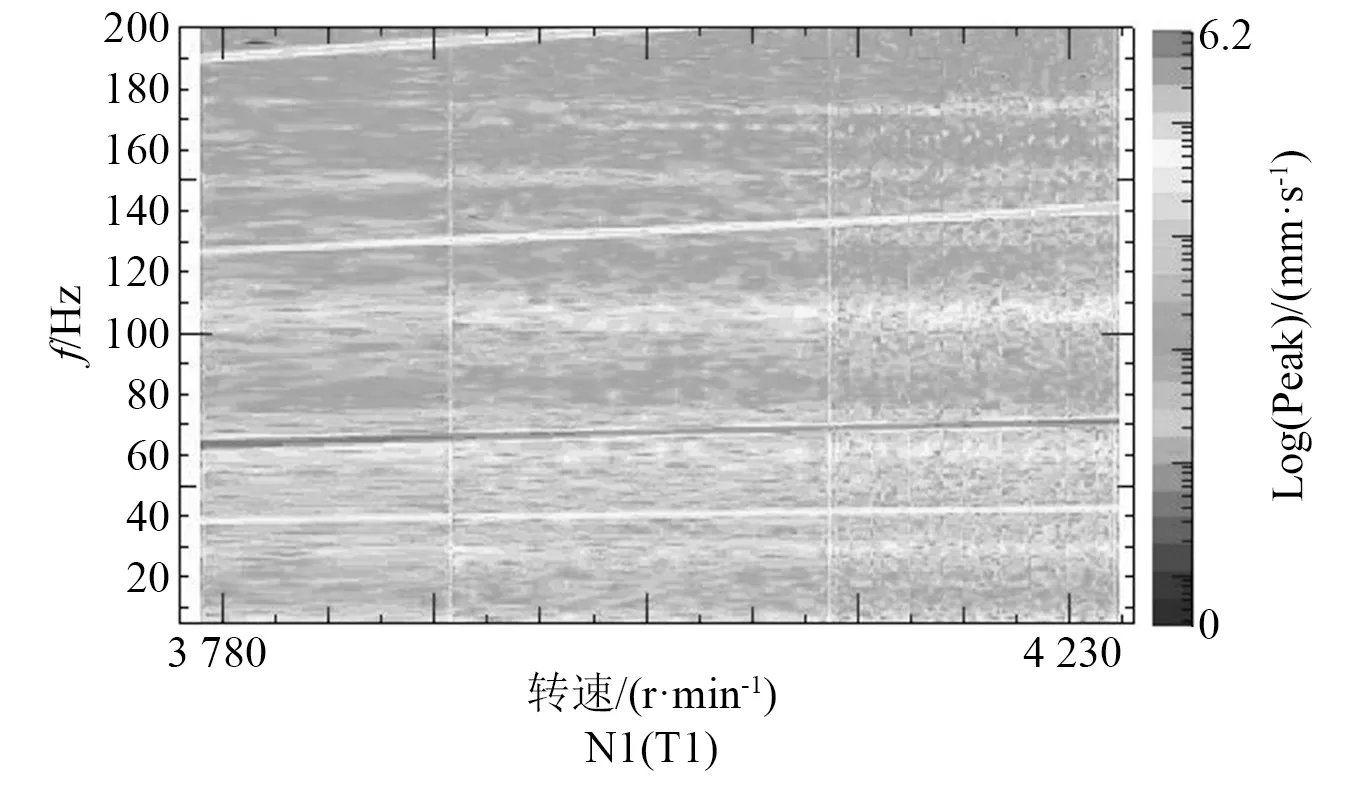
图18 整改后的测点振动瀑布图Fig.18 Waterfall map of test point after modification

4 结 论

基于本次增压级振动故障的特点，归纳行波共振的特点如下：①发生条件苛刻，转静子之间发生行波共振的条件相对比较苛刻，只有在转子转速达到特定条件下，转静子之间有碰磨，才激起了转子鼓筒后行波共振；②时间短、损害大，行波共振一旦发生，振动幅值在极短时间内飙升，导致严重的碰磨、碰撞事件，但这种损伤较大的振动其持续时间可能不长；③转速变化，行波共振将转子动能转化为静子件振动，可引起转动动能(转速)的变化；④碰磨痕迹的规律性，碰磨痕迹具有较强的规律性，特别是静子件上的磨痕，甚至可直接体现出振动的节径振型。

总结本次故障分析及排除过程，总结诊断方法如下：①基于能量法对转速进行分析，根据转速的变化锁定异常信号段，有针对性地进行小波分析、进行分段FFT对比分析；②根据磨痕推断异常振动的振型；③故障分析从推测故障频率、故障振型两方面着手；④提取轴心轨迹，辅助分析；⑤模态试验与模态仿真分析等技术的并用；⑥紧扣故障原因，采取针对性的改正措施。