基于传感器集群BLSTM模型的结构损伤定位
2022-12-01韩庆华党大智
韩庆华,马 乾,党大智,徐 杰
(1.天津大学 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室,天津 300350;2.天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300350;3.天津大学 建筑工程学院,天津 300350)
通过对结构表面布设的加速度传感器的振动数据进行分析,识别结构早期损伤并及时做出维护策略,对保证大型桥梁、大跨度空间结构等公共建筑在服役期间的安全性具有重要意义。按照难易程度划分,结构损伤识别大致分为三个层次[1]:判断损伤与异常是否存在(L1)、识别损伤位置(L2)和损伤程度(L3)。其中对于L1层次,研究学者已开展了大量研究,并基于信号分析与统计学理论提出多种损伤判断方法[2]。
相比于判断损伤与异常是否存在,在无监督模式下识别损伤位置和程度(L2和L3)相对更为困难。基于固有频率和振型等模态特征的分析是目前损伤定位的主要方法。近年来研究学者已构造了模态曲率[3]、模态应变能[4]等多种损伤敏感特征用于结构损伤定位。尽管模态特征参数对损伤位置信息较为敏感,但由于模态分析过程复杂、对传感器布置方式要求高,且固有频率等模态参数极易受环境影响等因素[5],导致其在实际工程的复杂结构损伤定位中应用存在一定难度。
因此,直接从加速度时域数据中提取特征,从而发现损伤位置和程度得到了更多学者的关注。时间序列建模是目前影响较大、效果较好的时域特征提取方法之一。近年来,利用自回归模型[6]、带有外生变量的自回归模型[7]、自回归滑动平均模型[8]和带有外生变量的自回归滑动平均模型[9]等时间序列模型,研究学者从振动信号中提取不同的损伤敏感特征,用于结构损伤定位。但线性时间序列模型对数据的平稳性等要求较高,在长期监测中应用有场景有限。基于神经网络模型对时序数据进行分析,可建立时序数据的内在非线性关联,相较于线性时间序列模型具有更高的泛化性,Yan等[10]将子结构技术与有外生变量的非线性自回归神经网络相结合,并使用统计推断标准F检验对结构损伤进行定位;Umar等[11]考虑邻近传感器信号之间的相关性,基于传感器集群的有外生变量的非线性自回归模型对振动数据进行预测,并基于预测残差的标准差与概率密度峰值构造损伤指标,实现无监督的结构损伤定位。有外生变量的非线性自回归模型的主要结构为前馈神经网络,前馈神经网络由于只考虑当前时刻输入对输出的影响,而不考虑其他时刻输入的影响,无法有效发现较长时间序列数据的规律。
长短时记忆神经网络是一种改进的循环神经网络,其通过门控结构保持训练时的梯度稳定,可以充分提取信号的时间特征。文献[12-13]利用长短时记忆神经网络对结构振动信号的时间依赖性进行学习,实现了不同结构损伤工况的分类。双向长短时记忆(bidirectional long short-term memory,BLSTM)神经网络是由前后两个方向的长短时记忆神经网络层对序列数据进行建模的网络结构,在处理时序数据的分类和回归问题中通常表现出比长短时记忆神经网络更高的性能[14],但目前利用包括BLSTM在内的长短时记忆神经网络结构进行损伤定位的研究均属于有监督学习方法,需要大量有标签样本进行分类模型的训练,在实际结构的损伤识别中具有很大局限性。
信息熵是表征系统信号状态的紊乱程度和无序性的度量[15]。各种故障诊断和损伤识别的研究表明,随着故障和损伤的发生,结构振动响应复杂性和离散程度增加,信息熵值随之增加。陈仁祥等[16]利用信息熵与融合无量纲指标,对旋转机械故障进行了诊断;项长生等[17]基于模态曲率效用信息熵,对梁结构损伤是否发生进行识别。
本文在上述研究背景的基础上,提出了一种基于传感器集群BLSTM神经网络模型的结构损伤定位方法,以进一步提高无监督模式下的结构损伤定位精度。首先通过定义传感器集群,利用基准工况虚拟脉冲响应函数(virtual impulse response function,VIRF)数据对不同传感器集群的BLSTM模型进行训练,进而通过训练好的模型对未知工况数据进行预测,通过基准工况和未知工况的模型预测残差的信息熵,提出了一种新的损伤识别指标,实现了结构的损伤定位与损伤程度判别。
1 本文提出的损伤定位方法
本文提出方法的核心是基于传感器集群BLSTM模型和信息熵的结构进行损伤定位。过程中首先对不同传感器集群的时间序列数据建立不同的BLSTM模型,然后利用基准工况的数据对BLSTM模型进行训练,进而利用训练好的BLSTM对未知工况的各个测点的数据进行预测,最后结合信息熵理论从模型的预测残差中提取损伤敏感特征来进行损伤定位。方法具体实施流程如图1所示,包括以下步骤:
步骤1对各工况下传感器采集的加速度数据进行降噪、去离群值等预处理,并根据多自由度结构的传感器布置特点,将传感器分为若干集群,其中每一个集群包括一个待测传感器以及一组与该传感器相邻的传感器;
步骤2选取某参考传感器的加速度数据作为虚拟激励,求解各传感器对应的虚拟脉冲响应函数,对其进行归一化处理后作为BLSTM模型的输入与输出;对每个传感器集群进行BLSTM建模,其中模型输入为该传感器集群中待测传感器及与该传感器相邻一组传感器的虚拟脉冲响应函数;输出为该传感器集群中待测传感器的虚拟脉冲响应函数;设置合理的BLSTM参数,利用基准工况数据进行模型训练,基于训练好的BLSTM模型,分别对参考工况(健康工况)和未知工况(待测工况)下各个传感器的虚拟脉冲响应函数进行预测;
步骤3计算参考工况(健康工况)和未知工况(待测工况)下各个传感器BLSTM模型预测残差,并基于预测残差的信息熵构造损伤指标,基于损伤指标确定损伤位置与损伤程度。
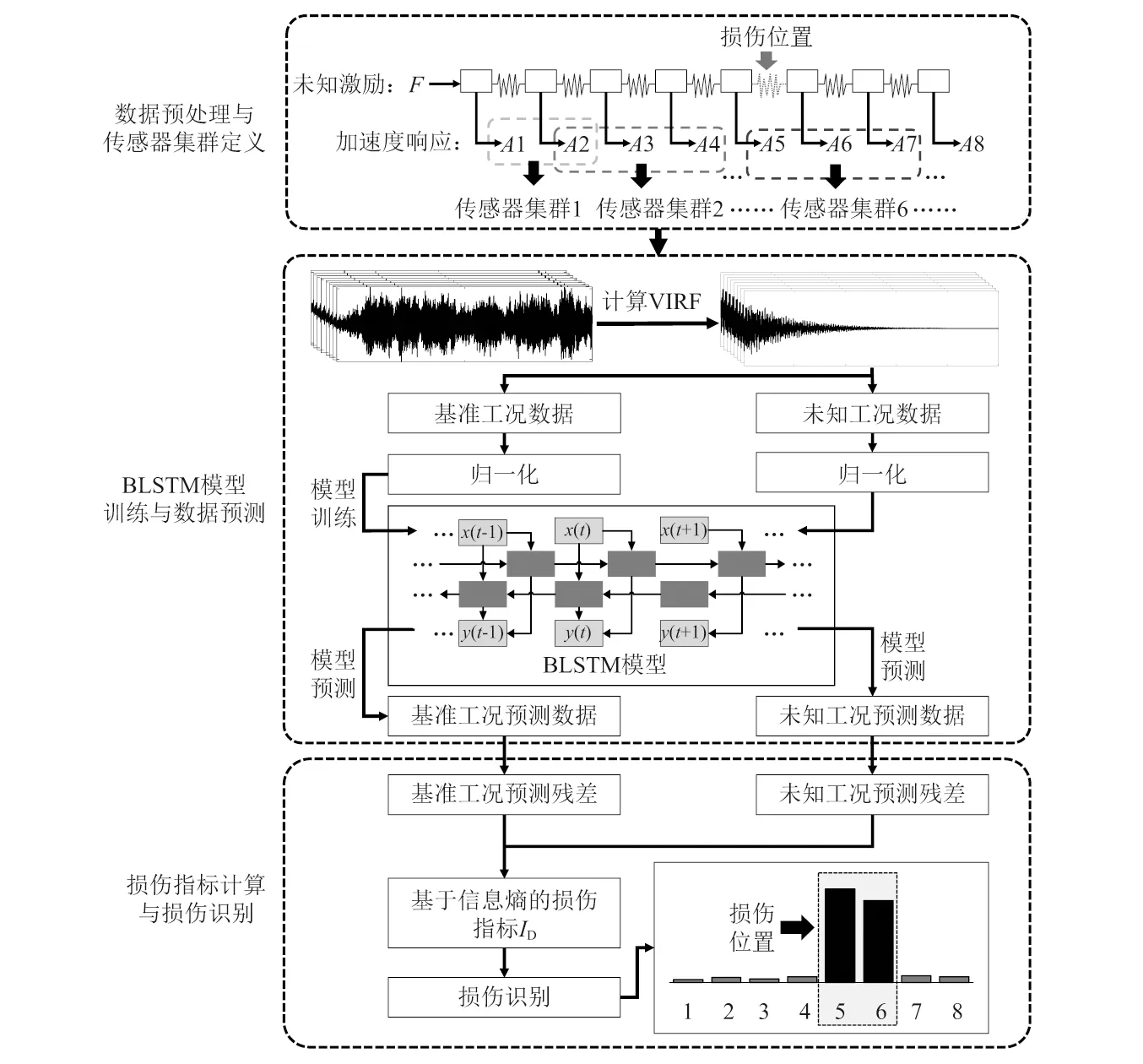
图1 本文方法的主要流程图Fig.1 The main flow chart of the proposed method
下面就本文损伤定位方法中所涉及的主要理论进行介绍。
1.1 传感器集群
在多自由度结构的损伤识别中,直接将所有测点的传感器数据作为输入BLSTM模型进行训练,往往导致结构复杂、计算效率低且最终的损伤识别效果较差。由于相邻测点的传感器数据往往表现出相似的特征,因此可以将相邻测点具有相似数据特征的传感器定义为一个集群[18],通过对传感器集群建立BLSTM模型,提高模型训练效率和损伤定位精度。以如图2所示的3自由度质量弹簧系统为例,简单说明传感器集群概念。该系统共设置了A1~A3三个测点,因此传感器被分为三个集群,其中每个集群包含一个待测传感器(BLSTM模型的输出)以及一组和该待测传感器相邻的其他传感器(BLSTM模型的输入)。

图2 3自由度质量弹簧系统的传感器集群Fig.2 Sensor clustering of 3DOF mass-spring system
1.2 双向长短时记忆神经网络
循环神经网络是以时间序列数据为输入,在序列方向按链式连接的神经网络。标准的循环神经网络具有一种简单的链式重复网络模块形式,例如图3(a)所示的tanh层。图3中:x(t)为当前输入信息;h(t-1)与h(t)分别为上一时刻和当前时刻的输出。循环神经网络中简单的链式结构在处理较长时序数据时,容易产生梯度消失及爆炸问题,长短时记忆神经网络通过引入具有多个门控结构的记忆单元,使网络具有控制内部信息积累的能力,有效解决了这一问题,其结构如图3(b)所示。

图3 循环神经网络结构与长短时记忆神经网络结构对比Fig.3 Comparison of recurrent neural network and long short-term memory neural network structures
长短时记忆神经网络的记忆单元中核心的部分为3种门控结构,分别为:决定当前记忆单元接受或遗忘上一记忆单元信息大小的遗忘门f(t)、决定当前记忆单元储存输入信息大小的输入门i(t)、决定当前记忆单元输出信息大小的输出门o(t),表达式分别为
f(t)=σ{Wf·[h(t-1),x(t)]+bf}
(1)
i(t)=σ{Wi·[h(t-1),x(t)]+bi}
(2)
o(t)=σ{Wo·[h(t-1),x(t)]+bo}
(3)
式中:W为权重;b为偏置项;σ为Sigmiod激活函数。记忆单元状态通过门控值进行更新
(4)
(5)
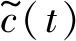
h(t)=o(t)·tanh[c(t)]
(6)
BLSTM的网络结构如图4所示,前向层从上一时间步迭代到当前时间步,后向层则与之相反。图4中,Cf(t)与Cb(t)分别为时间步t的前向层与后向层记忆单元状态。
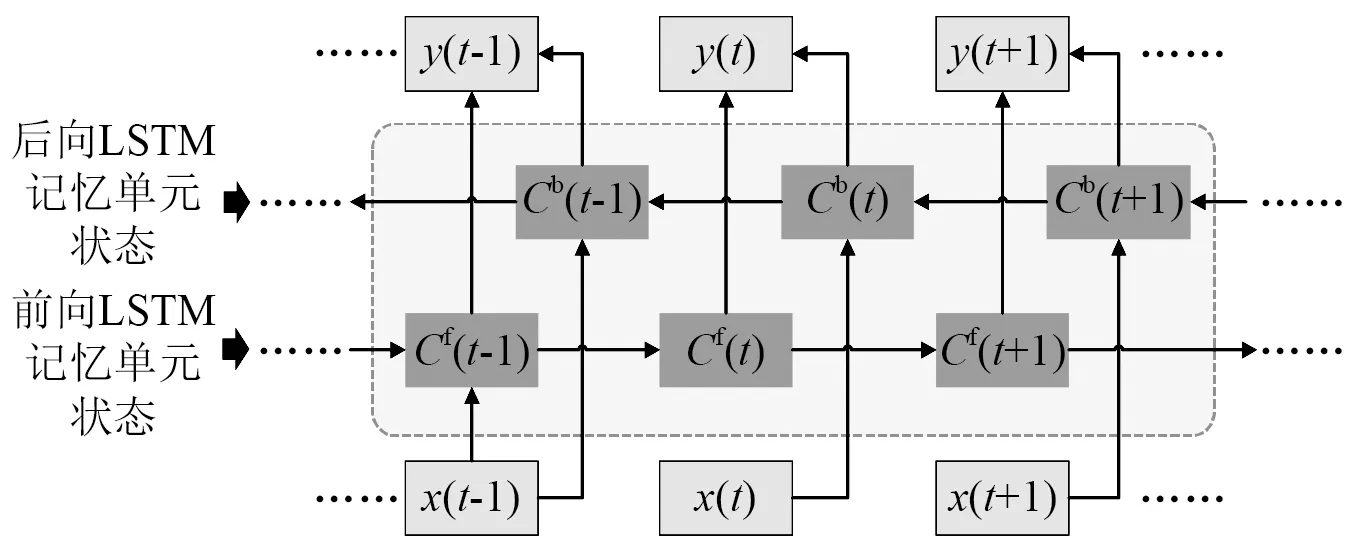
图4 BLSTM网络结构示意图Fig.4 Schematic diagram of BLSTM network structure
向前和向后两层长短时记忆神经网络单元的状态信息共同决定输出
(7)
式中,W与b分别为权重和偏置。
通过这种双向结构,BLSTM每个时刻的记忆单元状态都包含前后输入的信息,从而使网络可以更充分的学习序列的时间依赖性。在本文中,采用BLSTM对各个传感器集群的时域振动数据进行建模,模型的输入为各个传感器集群中所有测点的虚拟脉冲响应函数序列,模型的输出为传感器集群中待测传感器的虚拟脉冲响应函数序列。选取基准工况的数据对各传感器集群的BLSTM模型进行训练,进而根据训练好的模型,对未知工况数据进行预测。
1.3 基于信息熵的损伤指标
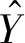
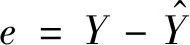
(8)
式中:e∈n×1为为参考工况(健康工况)或未知工况(待测工况)的BLSTM模型预测残差;n为采样点数。
信息熵是依赖于振动信号概率密度的统计特征,该特征根据PDF的直方图计算,用来表征信号的不确定性和随机性,对任意测点的模型预测残差,其信息熵表示为
(9)
式中,p(ej)为e中第j个信息出现的概率。当结构发生损伤时,模型预测残差的无序性和离散性增大,其信息熵增大,因此可进一步利用参考工况和未知工况的模型残差的信息熵构造损伤指标
(10)
式中,EH和EU分别为参考工况和未知工况BLSTM模型预测残差的信息熵。
2 试验分析与验证
2.1 8自由度质量弹簧系统试验验证
2.1.1 模型介绍
为研究损伤识别问题,洛斯·阿拉莫斯国家实验室设计了一个如图5所示的8自由度质量弹簧系统。该系统由7个弹簧(k1~k7)和8个铝合金质量块(m1~m8)连接组成,其中:k1~k7=56.7 kN/m;m1=559.3 g;m2~m8=419.4 g。所有质量块中间开孔,可沿高度抛光的圆柱形钢棒轴向水平滑动。使用峰值输出为215 N的激振器对质量块1施加水平方向随机激励,设置采样频率为500 Hz,通过加速度传感器记录每个质量块在各个设计工况下的加速度响应,每组试验采样时间8 s,共采集4 096个数据点。选取如表1所示的6种工况的试验数据验证本文方法的有效性。其中BC为基准(健康)工况,激励水平为5 V;HC1和HC2分别为激励水平为4 V和6 V的健康工况;DC1~DC3分别是不同激励水平(4~6 V)下的线性损伤工况,通过将k5弹簧刚度的降低14%模拟。
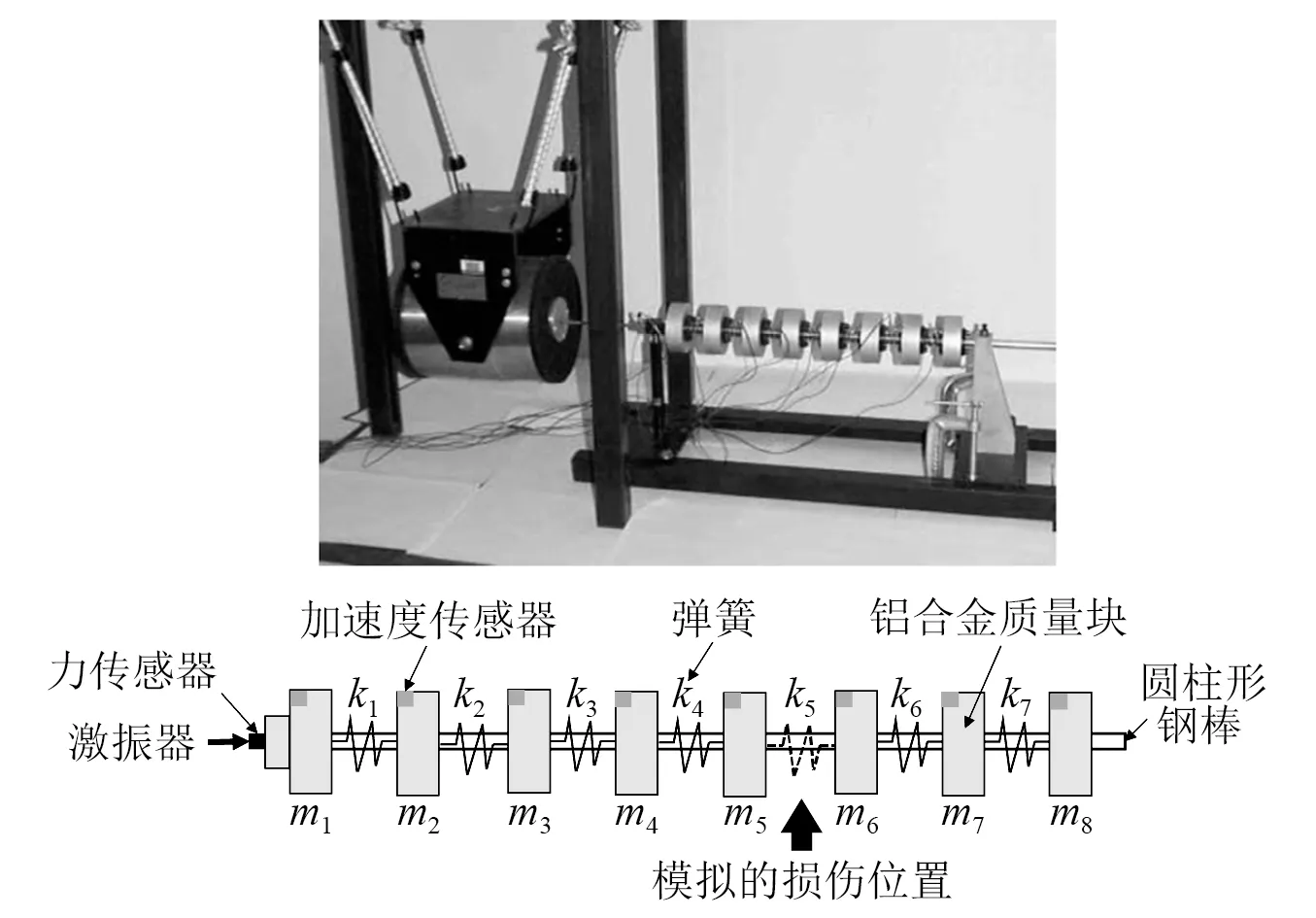
图5 8自由度线性质量弹簧系统Fig.5 The 8DOF mass-spring system
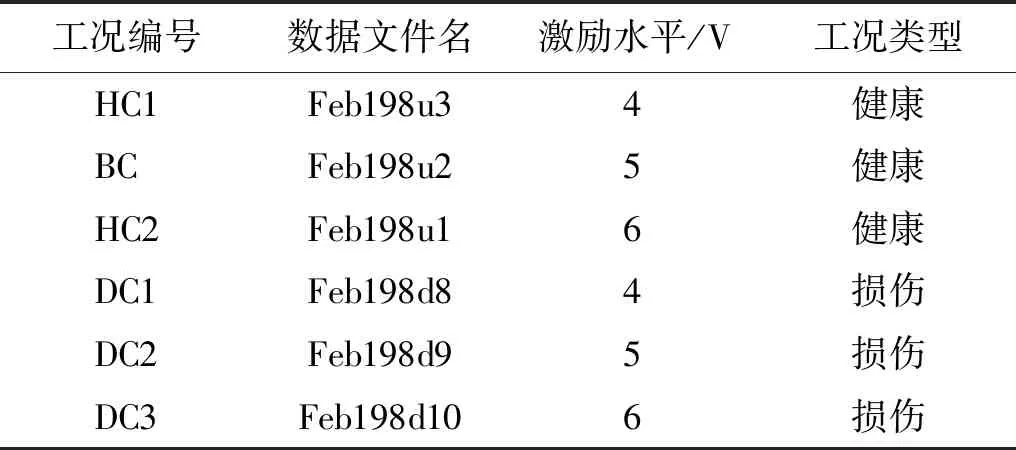
表1 6种工况试验数据Tab.1 Test data of the 6 conditions
2.1.2 传感器集群BLSTM模型建立
如第1章所述的损伤识别流程,首先定义该系统的传感器集群,根据传感器数量共创建了8个不同的传感器集群:集群1包括前两个传感器,其中第1个传感器为待测传感器,第2个传感器为其相邻传感器;集群2~7由第2~7个传感器中相邻的3个传感器依次组成,每个集群中间的传感器为待测传感器;群集8由最后两个传感器组成,其中最后一个传感器为待测传感器,第7个传感器为其相邻传感器。
基于振动时序提取损伤特征时,若直接将加速度原始数据作为BLSTM模型输入,可能会因外部激励的不确定性给识别结果带来干扰。为了排除这种干扰,可以利用激励与响应数据构造脉冲响应函数,进而基于脉冲响应函数进行时间序列建模。但是在实际结构监测过程中,外界激励通常无法获得,从而无法求解脉冲响应函数。为了在环境激励未知条件下获得更好的损伤特征,选取多自由度结构某参考点的加速度数据为虚拟激励,计算其他测点响应与虚拟激励的之间的频率响应函数[19],并对此频响函数做逆傅里叶变换从而得到虚拟脉冲响应函数。理论上,计算虚拟脉冲响应函数时可以选择任意传感器作为参考传感器,本文选取加速度数值相对较小的第8个传感器为参考传感器,将其加速度响应作为虚拟激励,设置傅里叶变换长度为4 096,计算各传感器的虚拟脉冲响应函数,并截取前1 000个数据,将其归一化到[-1,1]内,其中BC工况的虚拟脉冲响应函数如图6所示。
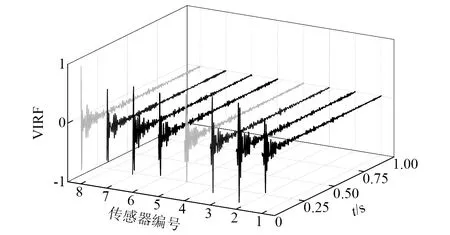
图6 BC工况归一化后的虚拟脉冲响应函数Fig.6 Virtual impulse response function of BC after normalization
分别对8个传感器集群建立相应的BLSTM模型,所有模型均由4层网络组成,第一层为序列输入层,其中输入为该待测传感器及其相邻传感器的虚拟脉冲响应函数序列,即集群中所有传感器的虚拟脉冲响应函数序列。第二层为BLSTM层,采用Adam优化算法求解,具有100个隐含单元,BLSTM层后连接全连接层与回归层,最终将序列数据进行输出,输出设置为每个集群中待测传感器的虚拟脉冲响应函数序列。设置最大迭代轮数为500,每次最小批处理数30,初始学习率0.01,利用BC工况数据对模型进行训练。
2.1.3 损伤识别结果分析
通过BC工况数据训练得到的各传感器集群的BLSTM模型后,对各个工况不同传感器的虚拟脉冲响应函数进行预测。以传感器1和传感器5的结果为例,说明BLSTM模型在损伤前后的数据预测效果。如图7所示,其中每幅图的上部分是损伤前(BC工况)的预测结果,下部分是损伤后(DC3工况)的结果。由图7可知,对于损伤前的数据,本文的BLSTM模型预测值与实际值吻合较好,说明训练得到的BLSTM模型能够较高精度地预测和表征未损伤结构的振动特征;对于损伤后的数据,本文的BLSTM模型预测值与实际值虽然存在一定的偏差,但这种偏差并不明显,通过损伤前后的预测值与实际值的直观对比并不能识别损伤是否发生。

图7 不同测点损伤前后实际值与模型预测值对比Fig.7 Identification results of different damage conditions
进一步求解BLSTM模型的预测残差,并对预测残差进行统计分析,绘制模型预测残差的分布直方和概率密度。其中传感器1和传感器5的在损伤前后的模型预测残差概率密度,如图8所示。由图8可知,相对于健康工况,损伤发生后模型预测残差的无序性增大,概率分布更为离散,且在靠近损伤位置处的传感器5的变化相对更为显著。
按照式(9)求解各个工况的不同传感器的模型预测残差的信息熵,并通过参考工况与未知工况的数据求解损伤指标ID,最终结果如图9所示。由图9可知,在HC1和HC2健康工况下,各传感器位置处的ID值均维持在较小水平(均值分别为0.13和0.06),说明通过BC工况数据训练得到各传感器集群的BLSTM模型,可对环境激励变化下的健康工况进行正确识别;在DC1~DC3工况下,各传感器位置处的ID相对健康工况明显增大,且损伤附近的传感器5和传感器6位置处的ID明显高于其他传感器,本文方法可对损伤位置进行较好定位。此外对比DC1~DC3工况可以看出,随着激励水平的增大ID随之增大,说明在确定的损伤程度下,ID对外荷载的较大变化也具有较好的敏感性。
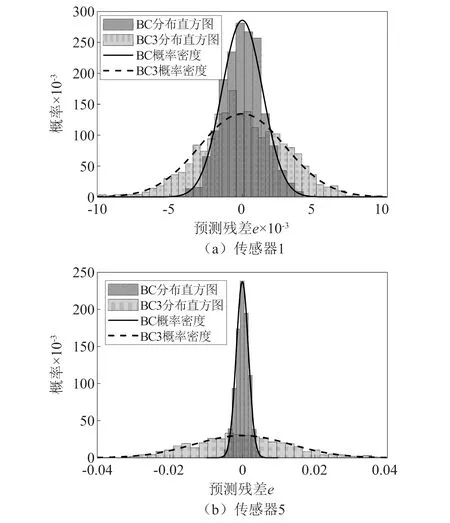
图8 不同测点损伤前后模型预测残差的概率分布对比Fig.8 Comparison of probability distribution of residual prediction before and after damage at different measuring points
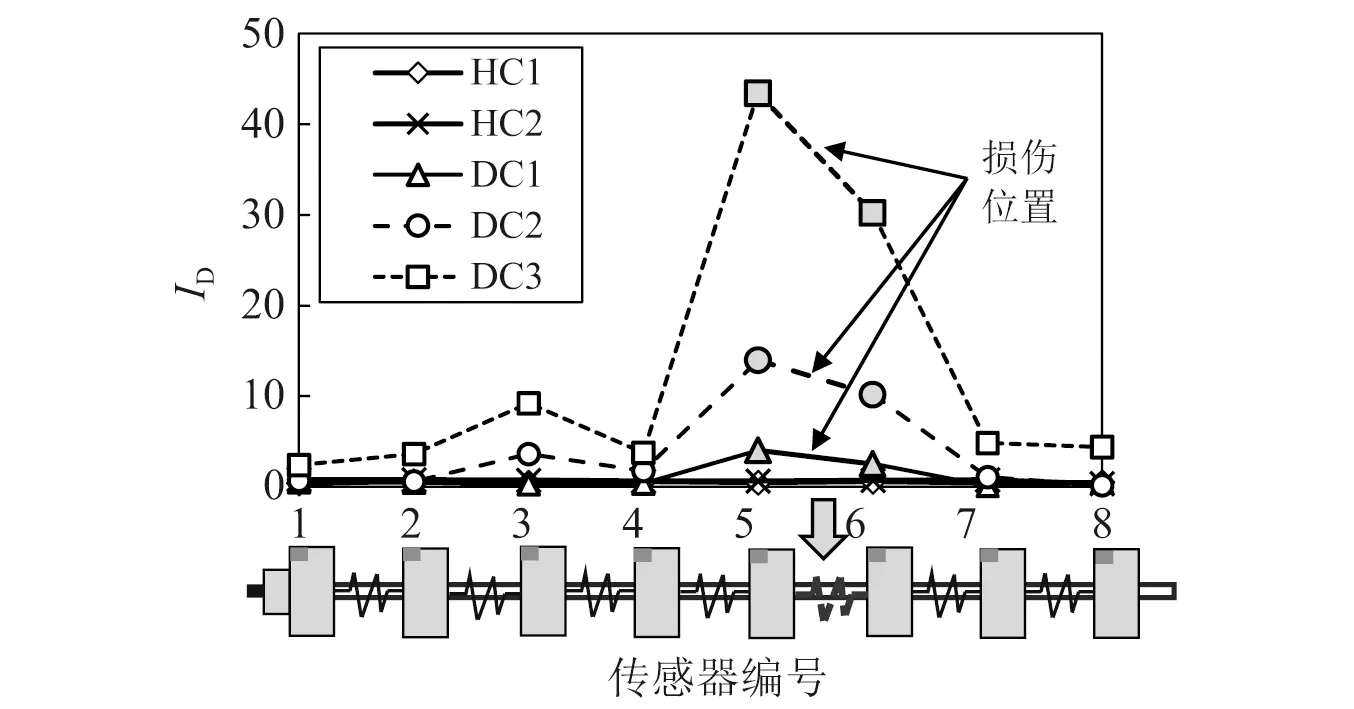
图9 不同工况的损伤识别结果Fig.9 Damage identification results of different conditions
2.2 工字钢梁模型试验验证
2.2.1 试验过程与数据采集
为进一步研究本文损伤识别方法的适用性,设计了如图10所示跨度为1 500 mm的工字型截面钢梁试验模型。钢梁横截面高140 mm,翼缘宽80 mm,腹板厚4 mm,翼缘厚5 mm。钢梁两端下翼缘底部通过螺栓固定,将钢梁沿跨度方向划分为(1)~(9) 9个单元,在除支座外的2~9节点上翼缘顶部布置了8个加速度器(A1~A8),传感器灵敏度为0.5 V/g;采用激振器对钢梁施加0.5~2 500 Hz的限带高斯白噪声激励,激振器出力峰值50 N,通过M5顶杆与4节点下翼缘底部相连。设置采样频率为4 000 Hz,分别设置健康工况与若干损伤工况,对各工况重复试验,采集简支梁上A1~A8传感器的加速度时程数据。通过在工字钢梁下翼缘底部分别切割长30 mm,宽为5 mm,10 mm和15 mm缝隙,模拟结构轻度、中度和重度3种不同程度的损伤,设置了4种损伤工况如图11所示。图11中:DC1~DC3为单元(3)位置处的单一损伤工况;DC4为单元(3)和单元(5)位置处的多损伤工况。

图10 工字钢梁尺寸及传感器布置图(mm)Fig.10 Dimensions and sensor layout of I-beam test(mm)
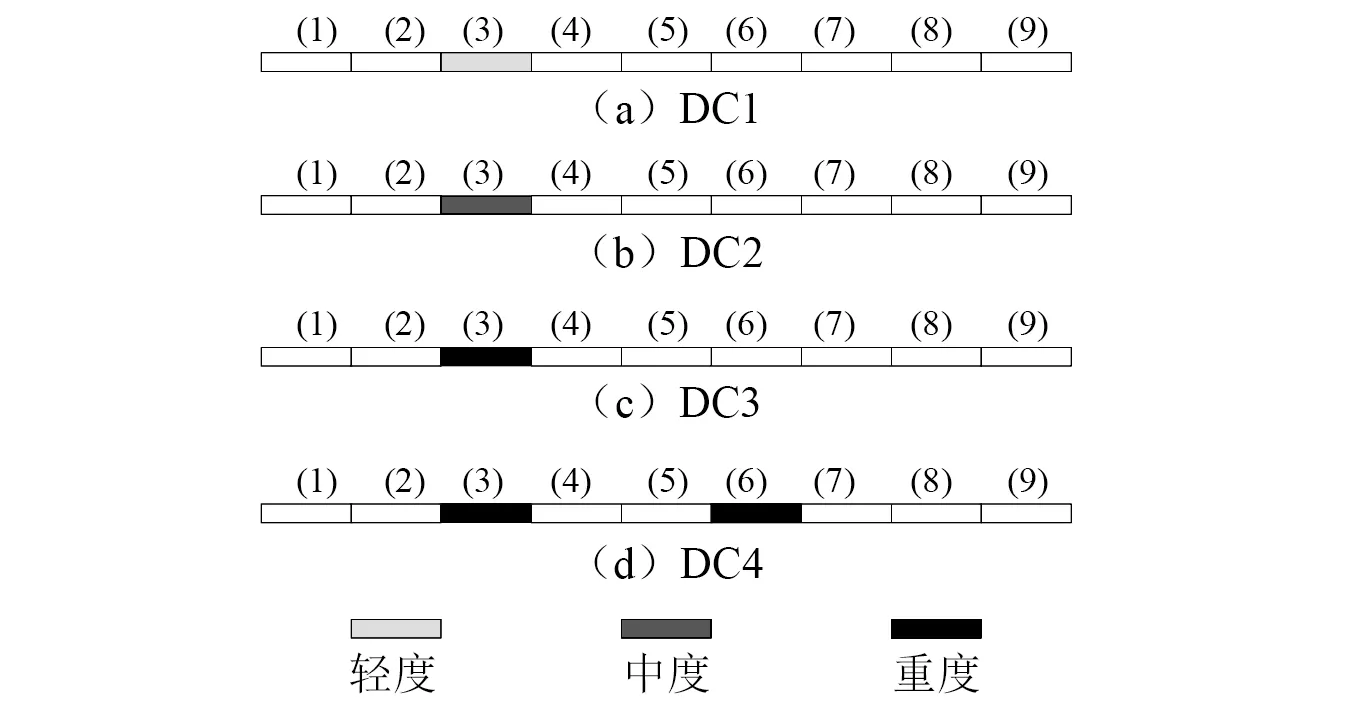
图11 模拟的损伤工况Fig.11 Simulated damage conditions
2.2.2 损伤识别结果分析
截取每个工况试验数据的中间阶段5 s时长加速度数据用于分析。与2.1.2节分析过程类似,按照本文的损伤识别流程,首先定义该结构的8个传感器集群,进而选取靠近支座的A1传感器为参考传感器,计算不同工况各个传感器的虚拟脉冲响应函数序列,并对其数据进行归一化,利用健康工况虚拟脉冲响应函数对8个传感器集群的BLSTM模型进行训练;通过训练好的模型对未知工况的虚拟脉冲响应函数数据进行预测并计算预测残差,最后利用预测残差信息熵构造的ID对损伤进行定位,结果如图12所示。由图12可以看出,对于不同的损伤工况,损伤发生处传感器的ID值明显高于其他传感器,说明本文提出的传感器集群BLSTM模型对单一位置损伤(DC1~DC3)和多位置损伤(DC4)均能较好的进行定位,且随着损伤程度的增加ID随之增大,说明本文提出的损伤识别指标同时也可较好的对损伤程度进行表征。

图12 不同损伤工况的识别结果Fig.12 Identification results of different damage conditions
3 桁架数值模型验证
3.1 模型介绍和数值模拟

图13 钢桁架试验模型Fig.13 Model of the steel truss
使用ANSYS建立该结构的有限元模型,对本文方法的有效性进行进一步验证。杆件采用BEAM188单元模拟弹性模量E=2.05×105MPa,材料密度ρ=7 850 kg/m3,泊松比μ=0.3。结构损伤通常表现为单元刚度的降低,本文中通过将原杆件替换成14.0×3.0 mm钢管,模拟50%的单元刚度损失。共模拟了8种损伤工况,如表2和图14所示。其中:DC1~DC4为单一损伤工况;DC5~DC8为多损伤工况。设置采样频率为200 Hz,每个工况持时20 s,共4 000个数据点。对结构整体施加垂直方向白噪声加速度,模拟自然环境下的地脉冲激励。采集如图14所示的结构下弦1~13号节点处的加速度响应用于后续损伤定位。
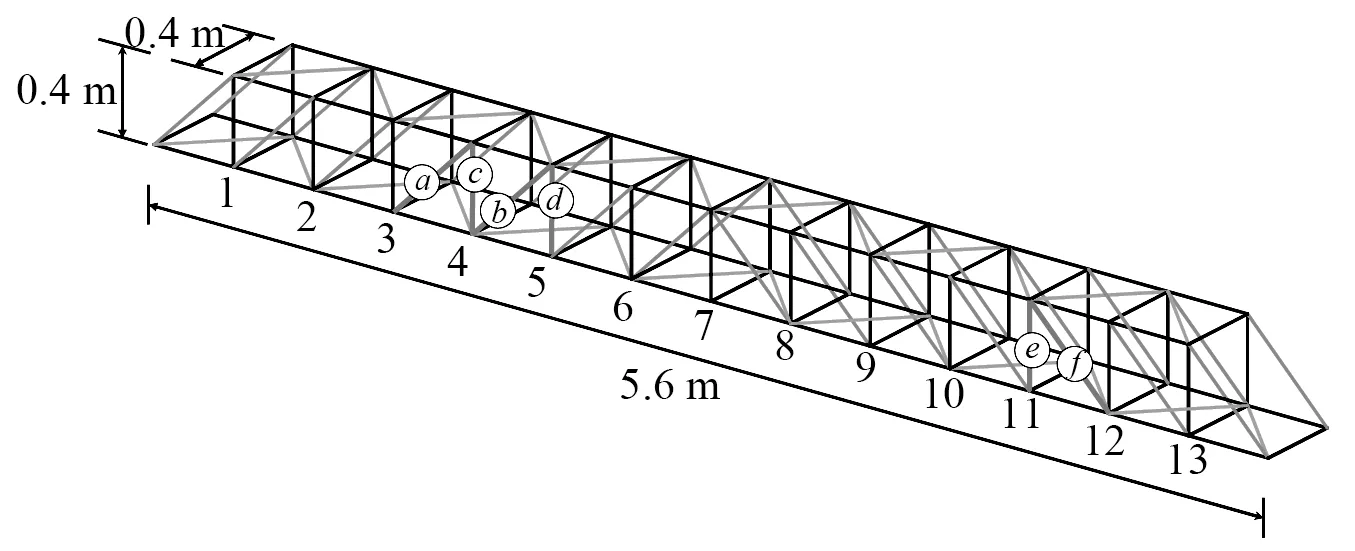
图14 模拟的损伤位置及传感器位置示意图Fig.14 Simulated damage location and sensor location schematic
3.2 损伤定位结果分析
按照第1章损伤定位流程,首先定义传感器集群。共创建了13个不同的传感器集群,集群1包括前两个传感器,其中第1个传感器为待测传感器;群集13由最后两个传感器组成,其中最后一个传感器为待测传感器;其余传感器集群为中间相邻3个传感器。选取第1个传感器为参考传感器,将其加速度响应作为虚拟激励,计算各传感器的虚拟脉冲响应函数。分别对13个传感器集群建立相应的BLSTM模型,建模过程与第2.1.2节所述类似,不再赘述。利用预测残差信息熵构造的ID对损伤进行定位,损伤定位结果如图15和图16所示。由图15可以看出,对于单一损伤工况,本文提出的损伤定位方法可以对损伤发生位置进行精确定位;对于多损伤工况,本文设计了两种损伤类型,即相邻杆件和不相邻杆件同时发生损伤的工况。由图16也可以看出,当损伤发生在相邻杆件或不相邻杆件时,本文方法均可进行较好的定位。

图16 多损伤工况的识别结果Fig.16 Identification results of multiple damage conditions
3.3 抗噪性分析
以损伤工况DC2为例,进一步说明本文方法的抗噪性。考虑3种噪声工况,信噪比β分别为60 dB(低噪声)、40 dB(高噪声)和20 dB(超高噪声),在监测得到的原始加速度响应数据中按照如下公式添加不同程度的高斯白噪声
(11)

为了便于分析不同噪声水平对本文方法的影响,对每个噪声工况不同传感器的ID进行归一化处理
(12)
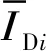
(13)
式中,id为编号,对于DC2工况,id=4~5。
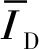

图17 不同噪声水平下DC2工况的识别结果Fig.17 Identification results of DC2 under different noise levels
4 结 论
提出了一种基于传感器集群BLSTM模型的结构损伤定位方法,通过不同传感器集群的BLSTM模型的建立,对不同位置处的虚拟脉冲响应函数进行了预测,并通过基准工况与未知工况模型预测残差的信息熵构造损伤识别指标,依此进行损伤定位。通过8自由度质量弹簧系统试验、工字钢梁模型试验,以及桁架结构数值模拟对方法进行了验证,得到了以下结论:
(1) 通过基准(健康)工况的虚拟脉冲响应函数训练得到的BLSTM模型,能够较高精度地预测和表征未损伤结构的振动特征,可对环境激励变化下的健康工况进行正确判断,具有较好的环境适应性。
(2) 相比于健康工况,损伤发生后模型预测残差的无序性增大,概率分布更为离散,且在靠近损伤位置处的传感器的变化相对更为显著,通过本文提出的基于模型预测残差信息熵的损伤指标,可对单一位置和多位置的损伤进行准确定位,而且可通过同一位置处损伤指标的变化对损伤程度进行判别。
(3) 随着噪声水平的增大,损伤发生处传感器位置的损伤指标减小,但即使对于超高噪声水平,损伤发生处传感器位置的损伤指标仍明显高于其他位置,本文方法仍能较好的识别损伤位置,具有良好的抗噪声干扰能力。
