基于FDA-LSTM的冷轧过程多源异构时序数据处理及颤振预测
2022-12-01赵潇雅郜志英周晓敏宋寅虎
赵潇雅,郜志英,周晓敏,宋寅虎
(北京科技大学 机械工程学院,北京 100083)
随着“工业4.0”和“中国制造2025”等国家战略[1]的提出,大数据对传统工业技术带来了革命性的挑战和颠覆性的创新,而5 G时代的到来,更是对工业物联网产生的海量大数据质量监控与分析提出了更高层次的精准性和时效性要求[2-3],同时深度学习算法和工业人工智能使对多场多态海量数据信息进行特征提取与信息挖掘成为可能。目前数据处理面临的三大挑战[4]是错误的数据导致决策错误,数据不能直接重构现场结果,将数据转化为有用的知识和决策。
板带钢作为各种工业产品的原材料,在工业生产中起着举足轻重的作用,对板带质量要求的提高也成了竞相研究的热点。我国的板带钢产业正面临着向智能制造转型的重大需求,板带钢生产过程中已经产生并积累了大量数据,在积累的工业大数据中,时间序列数据是最基本和最普遍的数据形式,因此对基于采样时间点的时序数据的分析挖掘,能够解决工程应用中的实际问题。在冷连轧过程中,由于轧制过程数据为多源数据采集系统采集到的多特征数据,存在采样频率不一致的问题,故需对数据进行频率协同,建立一一对应的完整可用的样本空间。针对离散样本的扩充问题,可将离散数据转化为连续函数,再以相同的步长读取数据。Ramsay等[5-7]提出了函数型数据分析方法,给出了完整的理论框架和分析计算方法,定义其本质是将数据看作整体,而不是离散的采样点。黎敏等[8]引入函数型数据分析方法将三维数据中的每个变量沿时间方向进行函数拟合,从而将三维离散数据矩阵转化为二维函数矩阵。并对各个变量曲线求取二阶导数,消除非平稳生产状态所导致的均值波动现象,增加建模的准确性。徐钢等[9]根据熔池反应所处的不同阶段,利用函数型数据分析方法建立吹炼前期和吹炼后期的函数型预测模型。
轧机颤振是影响板带质量最主要的原因之一,近年来国内外学者们[10-12]针对轧机颤振的建模与机理进行了一系列研究,分析得到了轧机颤振模型及影响轧机颤振的相关参数[13]。但影响颤振的相关因素较多,在工程实际应用中难以调控每一个参数,故需进一步筛选出与颤振相关性较强的参数。同时特征选择[14]可以减少输入数据的维度而减少模型复杂度,以筛选出对预测结果影响较大的特征。
由于生产过程的复杂性,物理模型的建立会引起明显的误差,机器学习经过特征提取和训练过程,可揭示输入和输出之间隐藏和模糊的相关性。神经网络可自动学习提取有用的特征,而不是由人工设定。因此,当数据丰富时,深度学习比传统的机器学习方法获得更好的性能。国内外学者利用多种神经网络对颤振等故障进行了智能检测,Liu等[15]提出了基于反向传播神经网络 (back propagation neural network,BPNN) 与遗传算法 (genetic algorithm,GA) 的颤振状态辨识模型,即BPNN-GA模型。谢锋云等[16]提出基于广义区间理论的广义BP神经网络切削颤振识别模型,利用广义区间不确定性分析方法将测量不确定性量转换为广义区间量,并进行广义区间形式的时频特征提取,最后将广义区间化的特征量代入广义BP神经网络识别模型中,对切削加工状态进行识别。Kumar等[17]将输入信号的均方差作为衡量颤振的指数参数,通过这些输入和输出参数,使用自适应神经模糊推理系统训练颤振模型。刘阳等[18]基于长短时记忆 (long short-term memory,LSTM) 循环神经网络建立轧机颤振能量值的智能预报模型,利用轧件规格、轧辊状况、轧制工艺以及轧机振动状态的历史信息数据,对最为典型和振动频繁的第五机架振动能量值加以预测。
本文针对冷连轧生产过程中的颤振问题,进行多源异构时序数据的分析与信息挖掘,改善工业时序数据来源广泛、价值密度低、动态性强的缺陷,找到数据的统计规律以及不同物理特性的数据间的关联性,从而建立颤振预测模型,以指导实际生产。
1 基于FDA的多源异构样本数据
1.1 函数型数据分析
函数型数据分析方法将离散时间序列进行函数表达,即
yi,j,k=x(tk)+εi,j,k,k=1,2,…,K
(1)
式中:x(tk)为原始数据序列的函数在第k采样点的函数值;εi,j,k为该点对应的拟合误差,代表观测数据中扰动因素、误差或其他外生因素;拟合后的yi,j序列可以表示为函数xi,j(t)。
函数型数据分析的一般步骤为:
步骤1用基函数平滑法对离散数据进行展开。
基函数平滑法本质是将N个基函数线性组合,得到原始离散数据的函数表达,对于变量j,由Nj个基函数φj(t)=[φj,1(t),…,φj,Nj(t)]T的线性组合表示函数xi,j(t),公式表示为
(2)
式中:xi,j(t)为拟合函数;ci,j=[ci,j,1,…,ci,j,Nj]T为系数向量。
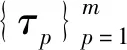
(3)
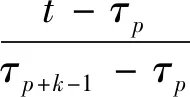
(4)
步骤2添加惩罚项对拟合函数进行光滑
利用基函数平滑法对数据进行拟合时,拟合函数应对原始离散数据的主要特征尽可能地进行表达,为了应避免曲线过度拟合,导致曲线过度的波动或局部变化,引入粗糙度惩罚因子对曲线的拟合程度进行控制,使得离散数据的函数化表征更加合理。粗糙惩罚法是在基函数法的基础上,通过增加惩罚项来对拟合曲线的曲率进行控制。
通常以二阶导数平方的积分作为测度曲线的粗糙程度的惩罚项,即
(5)
由式(1)可知,拟合函数可写成系数向量与基函数乘积的形式,将其代入式(5)得
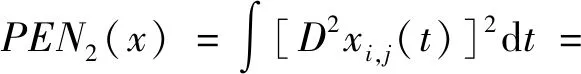
(6)
步骤3采用最小二乘法计算系数向量
系数向量ci,j的估计采用最小二乘法,即最小化残差平方和
(7)
式中:yi,j=(yi,j,1,…,yi,j,k,…,yi,j,K为原始数据;λ为惩罚因子的系数,平衡曲线拟合程度和曲线光滑程度。
定义ΦK×Nj为基函数矩阵在各观测时间点上的取值,即
(8)
基于最小二乘法求解未知参数的方法,解得系数矩阵ci,j为
ci,j=(ΦTΦ+λR)-1ΦTyi,j
(9)
采用广义交叉验证方法(generalized cross-validation,GCV)求解惩罚系数λ的值,公式为
Sφ,λ=Φ(ΦTΦ+λR)-1ΦT
(10)
df(λ)=traceSφ,λ
(11)
(12)
式中:K为采样点个数;λ在一定实数范围内进行取值,当GCV(λ)的值最小时所对应的λ值即为惩罚系数。
1.2 基于FDA的样本扩充
冷连轧生产过程数据采集系统采集到的数据主要包括振动数据采集系统采集到的振动能量数据、以及过程信息采集系统采集到的工艺参数数据。由于工业生产中采集到的多源异构时序数据存在大体量、多源性、连续采样、价值密度低等问题,故需对原始数据进行数据预处理,包括数据转换、数据清洗及时刻匹配,如图1所示。
经数据预处理可得,工艺参数数据采样间隔为5~8 s,振动能量数据采样间隔为0.2 s。同时,分析冷连轧过程中产生的BPC数据可知,一些变量随着时间发生波动,具有函数性质的特征,且变量与变量之间存在非线性关系,因此可采用函数型数据分析的方法对样本进行扩充。
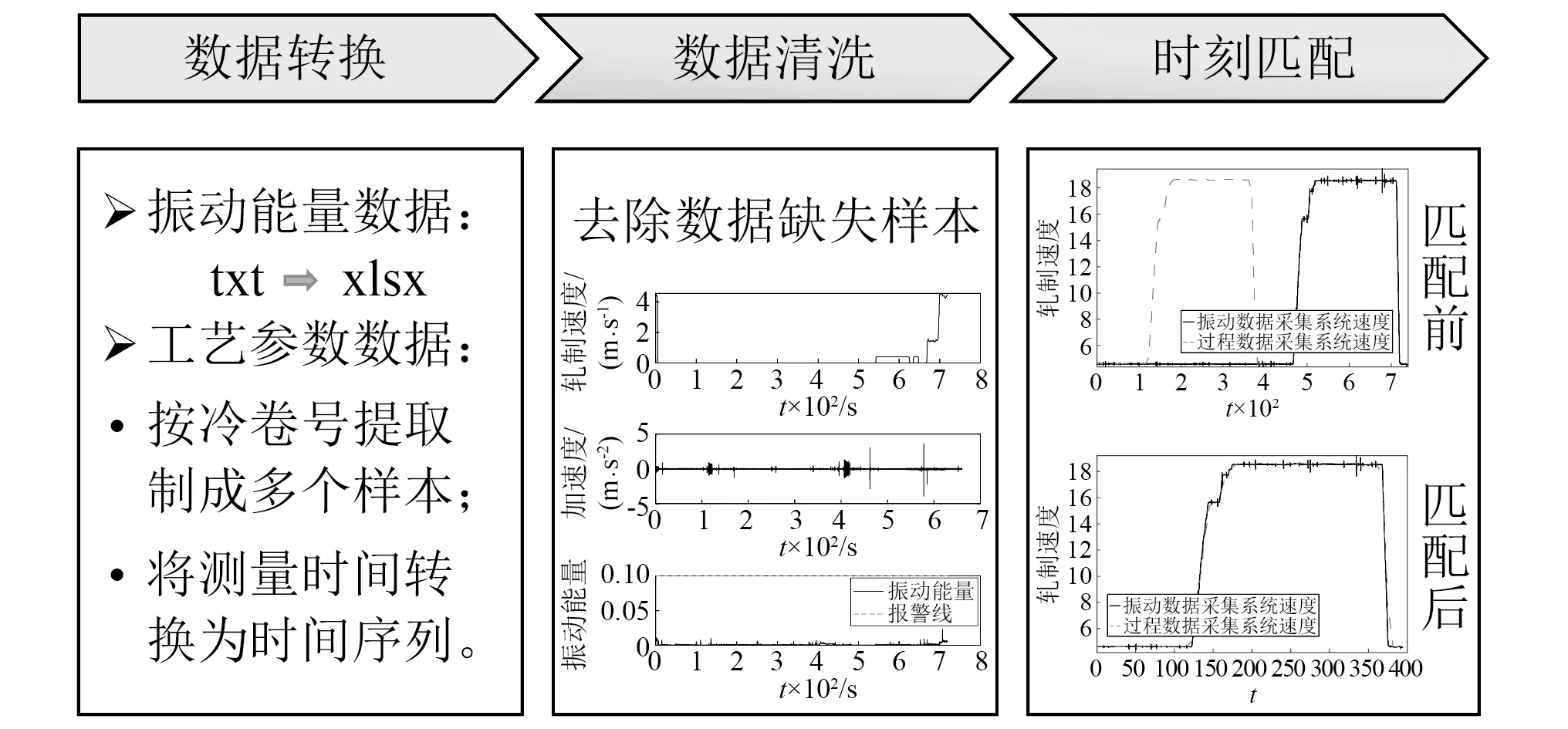
图1 数据预处理步骤Fig.1 The steps of data preprocessing
轧制速度、轧制力等为非周期信号,因此选用含有多重节点的B-spline基函数作为拟合的基函数可更好实现地实现函数化的表达,且B-spline基函数有着很多优良的性质,有利于更深层次的数据分析。本节的BPC数据扩充步骤如图2所示。
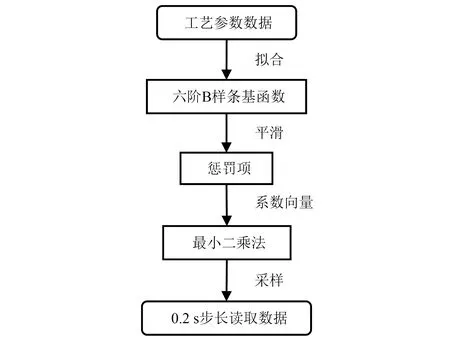
图2 函数型数据分析算法步骤Fig.2 The steps of functional data analysis algorithm
以轧机第五机架的带钢速度为例进行函数拟合和插值,如图3所示。
由图3可得,函数型数据分析对数据的函数表达有一定的光滑度要求,最小二乘法拟合的方法可通过在最小二乘法的拟合标准均方差中加入粗糙度惩罚项实现函数光滑甚至导数的光滑的性质,函数型数据拟合的在处理突变位置有更好的效果,曲线更平滑,故本文采用函数型数据分析的方法实现样本的扩充。
1.3 不同工艺参数的拟合效果
由于轧制过程复杂,每一卷轧制的时长不一致,为便于观测多卷数据的函数型拟合效果,对采样时间进行归一化处理
(13)
式中:tk为第k个采样点时间;Tk为归一化后第k个采样点时间;N为每一卷轧制的总时长。

图3 函数型数据拟合和插值效果对比图Fig.3 Comparison chart of the effect of functional data fitting and interpolation
归一化后,对部分钢卷的五机架带钢速度、四机架后张力进行函数型拟合,拟合效果如图4所示。
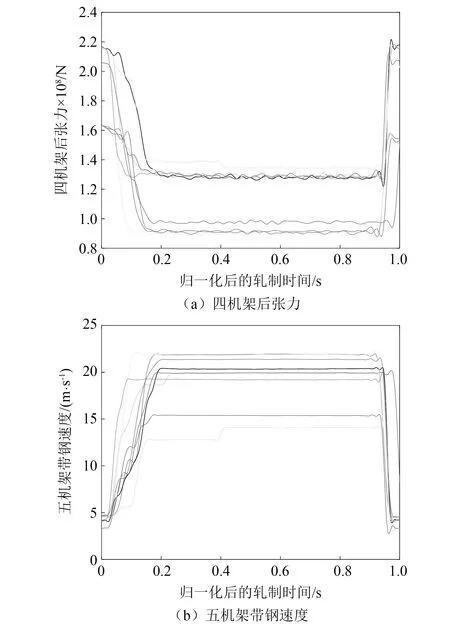
图4 函数型数据拟合效果图Fig.4 Fitting effect diagram of functional data analysis
2 特征选择及样本空间构建
2.1 特征选择
特征选择是利用一系列的规则,得到特征重要程度的相对关系,自动选择出对分类过程最重要的特征子集的过程。机器学习过程中,特征选择是非常重要的一步,一方面遗漏掉重要特征会导致模型拟合能力不足;另一方面冗余特征也可能会带来额外的计算量导致训练时间过长,以及模型过拟合,对新样本泛化能力不足等问题。因此只有选择了合适的特征,模型的训练才能成功。
特征选择模型分为过滤式、封装式和嵌入式3类[19]。在特征选择中,最适合在探索阶段使用的就是过滤式的方法,包括方差阈值法和单变量选择法。单变量特征选择有多种特征选择方法,本文采用基于样本相关系数的SelectKBest算法[20]对特征进行选择。
SelectKBest算法是一种统计测试方法,能够对每一个特征进行测试,衡量该特征和响应变量之间的关系,得到每个特征的重要性得分,去除得分不高的特征。具体算法如下:
步骤1对特征集X=(x1,x2,…,xN)和因变量y分别计算每一列数据的均值和标准差。
步骤2计算每个特征量xi和因变量y之间的样本相关系数r
(14)
步骤3检验正态假定下两个变量之间的相关性,用统计量f表示
(15)
步骤4判定假设检验结果,用统计量p表示,一般以p<0.05为显著,p<0.01为非常显著。
步骤5比较每个特征量的f和p值的大小对特征进行选择。
2.2 样本空间构建
本文以频繁发生颤振的第五机架为研究对象,以与颤振相关的工艺参数为特征量,振动能量值作为输出值,制作训练模型的数据集。首先根据轧机颤振模型得到可能影响颤振的工艺参数,如入口油膜厚度、出口油膜厚度、轧制速度、前后张力等。且五机架振动发生与四机架的振动状态相关,特征空间还应包括四机架的相关信息。因此,初步确定样本空间为包含15个工艺参数为输入特征以及一个振动能量值作为输出参数的数据集,每一卷数据为一个样本,原始样本空间如图5所示。
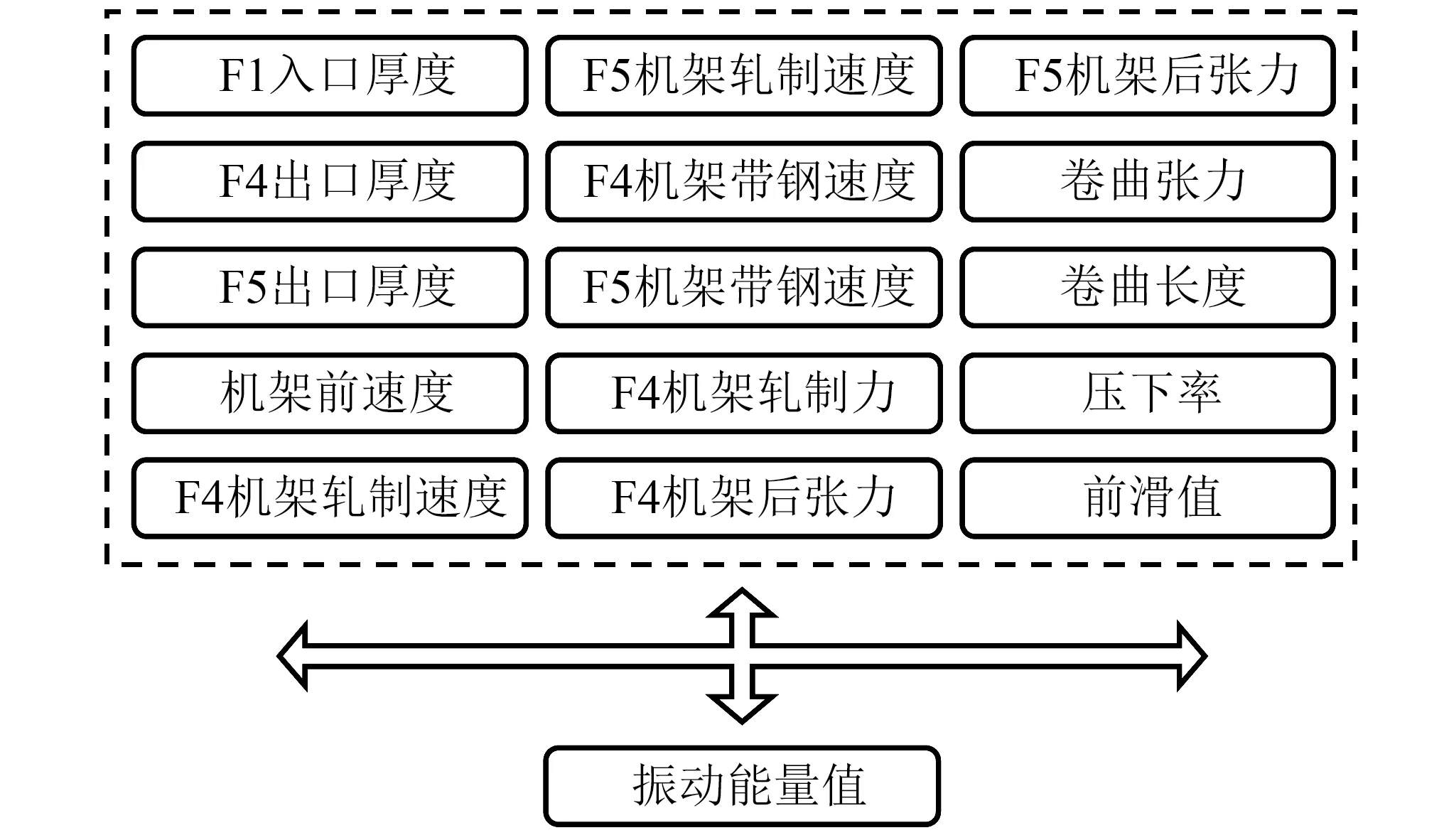
图5 原始样本空间Fig.5 Original sample space
选定原始数据集后再进一步进行特征量的选取:对于模型来说输入减少,复杂度降低,学习的速度上升。而对于实际应用来说,这15个特征对分类结果影响较大,实际发生振动时,从可行性上是不可能调节全部工艺参数的,这时候调节几个重要的特征就可以改变振动的结果,从而达到抑振或者消除振动的目的。
对原始数据集进行SelectKBest特征选择,统计量f和p的值如表1所示。
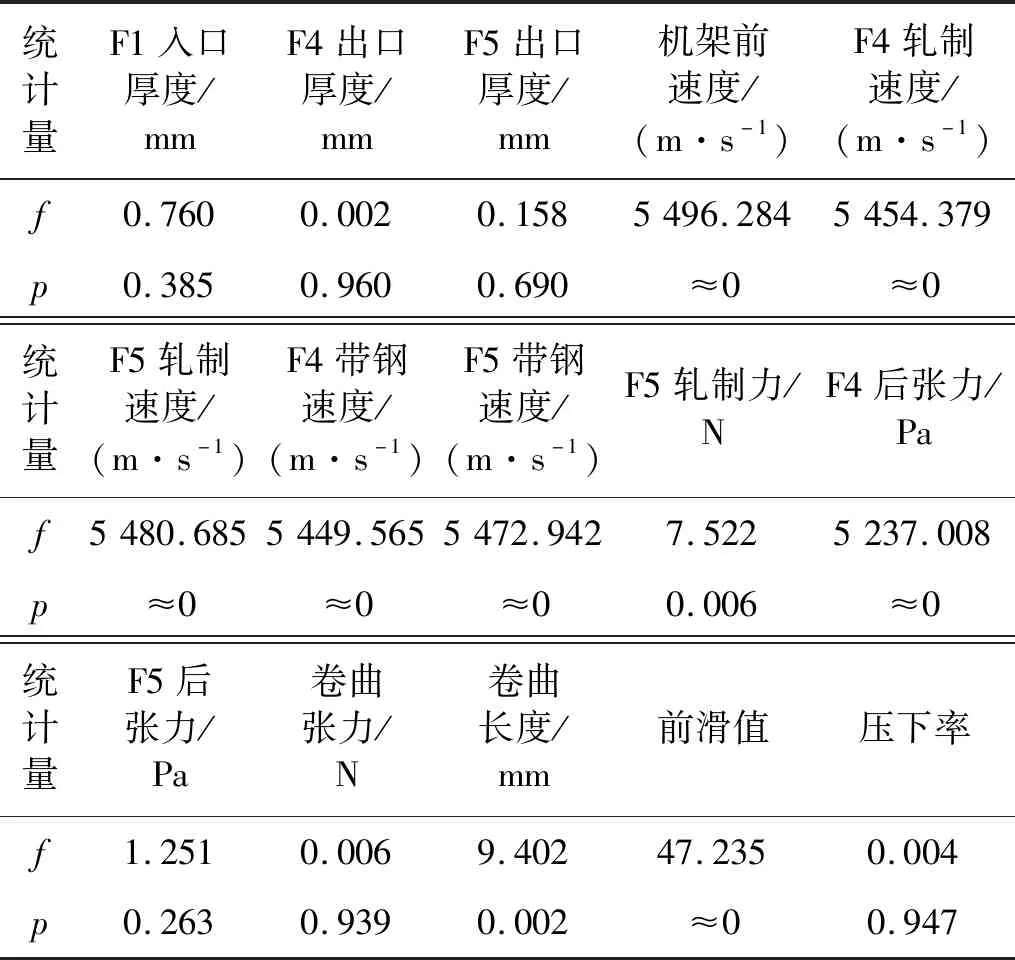
表1 各特征数据的统计量Tab.1 Statistics of each characteristic data
由表1可得,机架前速度、四机架轧制速度、五机架轧制速度、四机架带钢速度、五机架带钢速度、四机架后张力的f值均大于5 000,p值均约等于0。由此可得,这6个特征量与振动能量值具有很强的相关关系,故选取这6个特征量作为输入特征,从而建立如图6所示的样本空间。
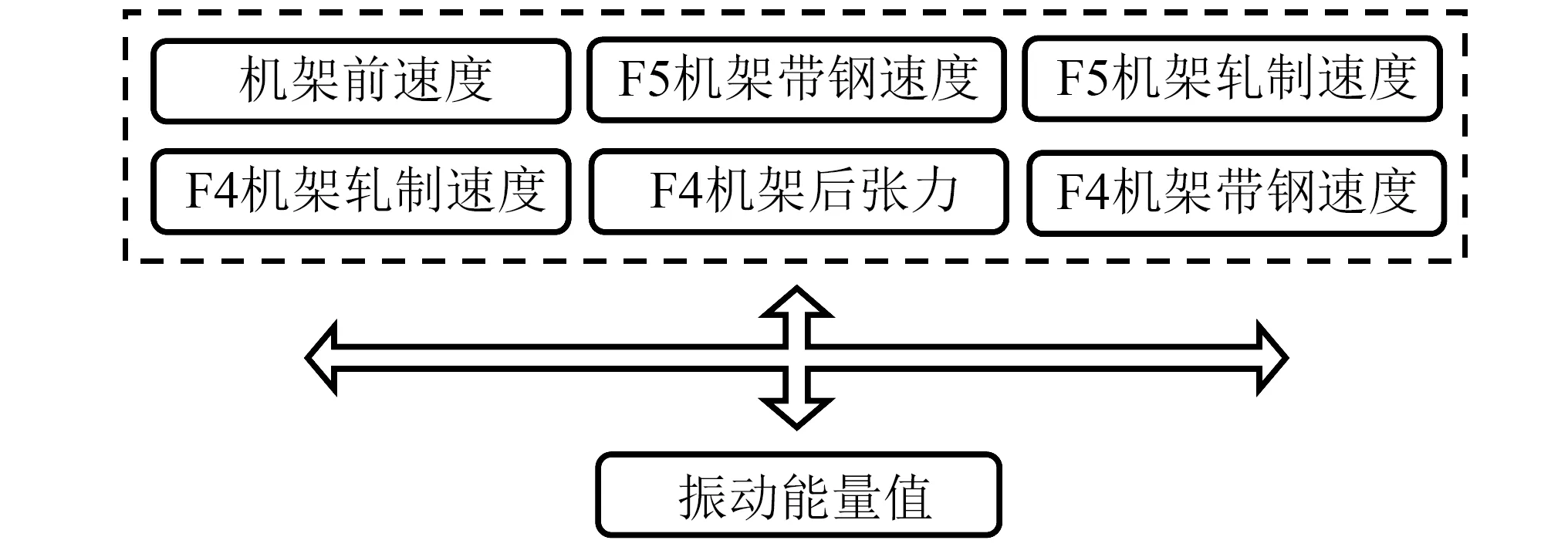
图6 特征选择后的样本空间Fig.6 Sample space after feature selection
3 基于LSTM神经网络的颤振预测
由于轧机颤振的发生有很强的时序性,与轧机的历史状态密切相关,基于此特性,轧机颤振的预测可转换为时间序列预测研究。而神经网络作为常用于处理序列问题的深度学习模型,可用于颤振的智能预测。因此,本文采用LSTM神经网络模型对颤振进行预测。
3.1 LSTM神经网络模型构造
LSTM神经网络的网络结构如图7所示,为单元状态加门限的结构:
(1) 单元状态——让输入向量沿时间轴向下流动,相当于一个传送带,传送带上的东西会随着通过的重复模块基于当时的输入有所增减,如图7(a) 所示,当前时刻单元状态Ct计算公式为
(16)
式中,it,ft分别为输入门、遗忘门的激活向量。
(2) 门限——在LSTM中由sigmoid函数、tanh函数和乘法加法控制的过程,包括遗忘门、输入门、输出门。
1) 遗忘门的结构如图7(b) 所示,其激活向量ft计算公式为
ft=σ(Wxfxt+Whfht-1+bf)
(17)
式中:x=(x1,x2,…,xT-1,xT)为输入的时间序列;h=(h1,h2,…,hT-1,hT)为隐含层序列;σ为激活函数,选取激活函数为sigmoid函数;W为权重矩阵;b为偏置向量。
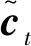
it=σ(Wxixi+Whiht-1+bi)
(18)
(19)
式中,f为激活函数,选取激活函数为tanh函数。
3) 输出门结构如图7(d) 所示,其激活向量ot及隐含层序列h的计算公式为
ot=σ(Wxoxt+Whoht-1+bo)
(20)
ht=otf(Ct)
(21)
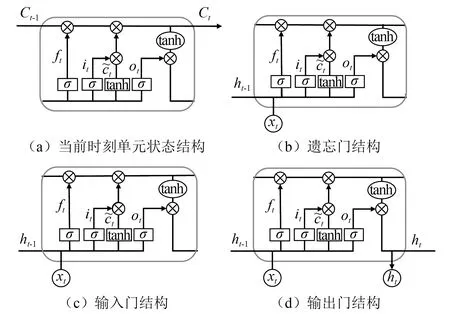
图7 LSTM神经网络结构图Fig.7 LSTM neural network structure diagram
采用步长为4的LSTM神经网络模型,即用历史4步的信息去预测未来第5步的输出,如图8所示。
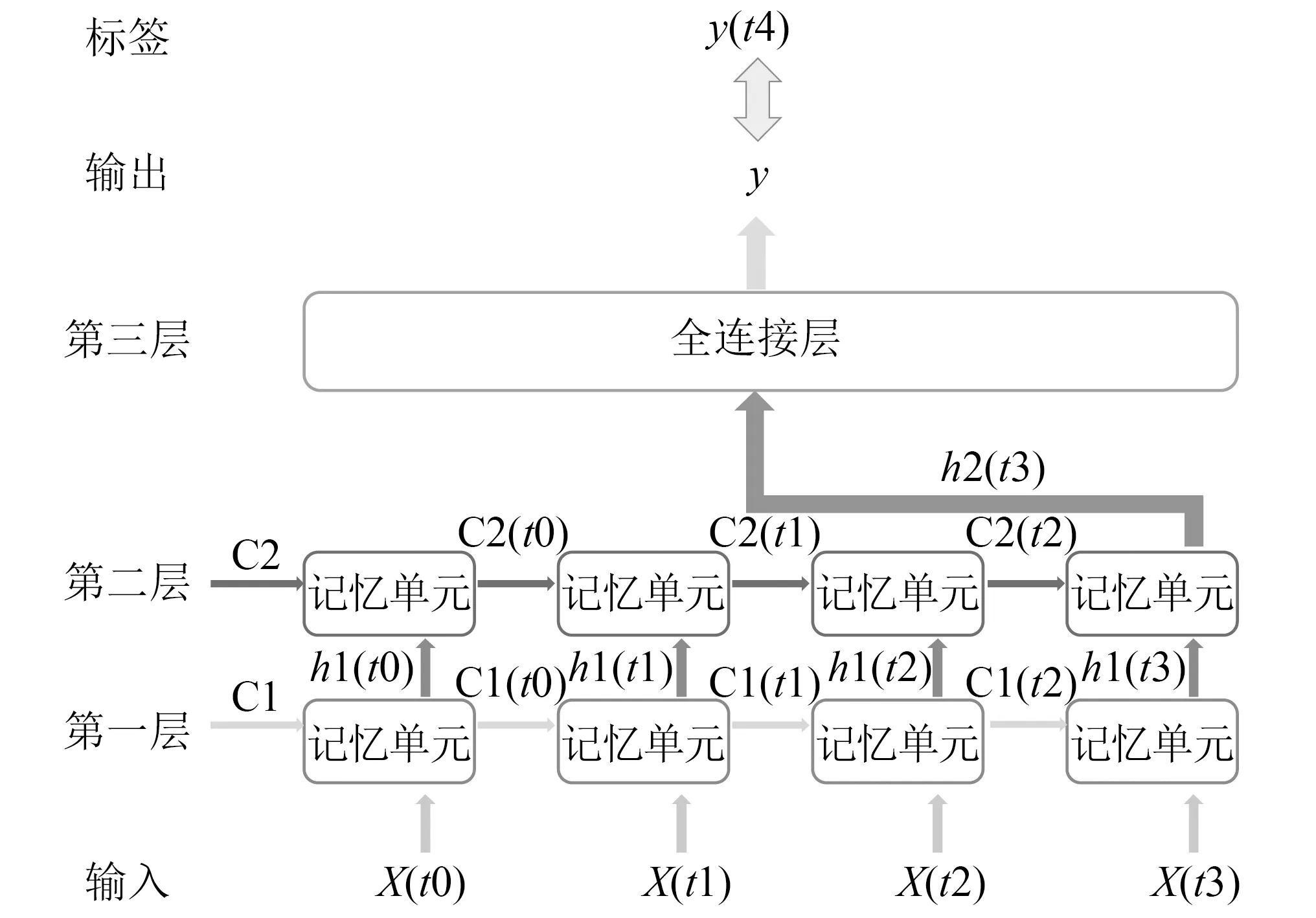
图8 步长为4的LSTM神经网络输出步骤Fig.8 LSTM neural network output steps with a step size of 4
同时,采用Adam 一阶优化算法替代传统随机梯度下降算法,它能基于训练数据迭代地更新神经网络权重W和偏置向量n。
神经网络算法的基本流程如图9所示。
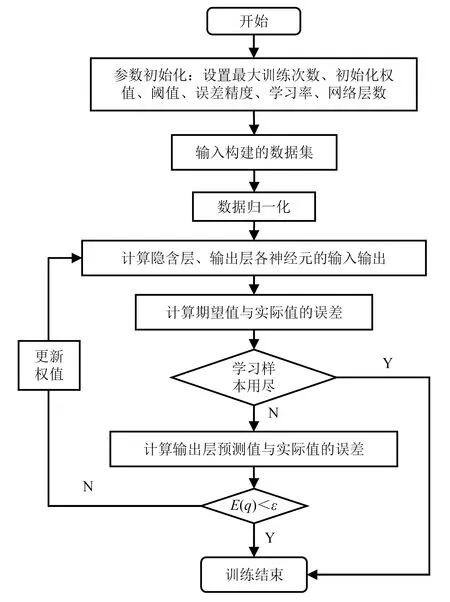
图9 LSTM神经网络算法流程图Fig.9 LSTM neural network algorithm flow chart
3.2 不同神经网络模型预测精度对比
选用已建立的样本空间作为观测数据进行模型的训练与测试,每一卷数据为一个样本,其中每一卷数据的80%用于模型的训练,20%用于模型的测试。同时为突出LSTM神经网络预测效果,采用RBF神经网络模型和RNN神经网络模型进行对比分析。对10卷样本进行训练并测试,部分预测效果如图10所示,测试集均方误差如表2所示。
由图10(a)可得,在1 440 s处振动能量值出现峰值,在此处RBF模型的预测峰值与实际峰值产生时间不一致,RNN模型的预测峰值只有较小的突增,LSTM模型预测峰值接近实际峰值。由图10(b)得LSTM模型相较于其他两个模型,其测试集预测结果的变化趋势与实际数据的变化趋势更加一致。同时表2的计算结果也显示LSTM神经网络模型测试集的均方误差最小。
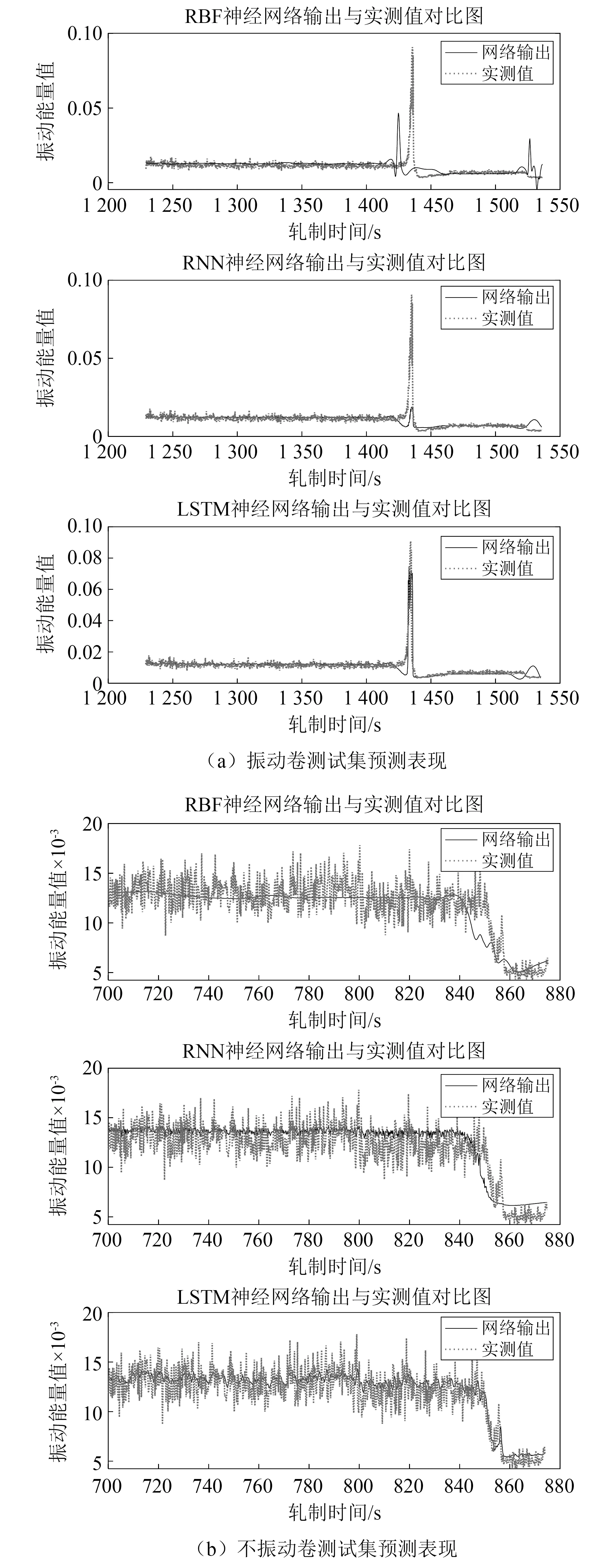
图10 三种神经网络预测效果对比Fig.10 Comparison of three kinds of neural network prediction effects
这是由于轧机振动能量值不仅与多个相互耦合的物理量相关,且与系统的历史状态相关,而RBF神经网络模型只能学习到该时刻的信息,从而会使网络学习到的信息不完整;RNN神经网络引入时间步长,允许信息持续存在,但其存在长时依赖问题,会产生梯度爆炸或梯度消失,影响预测精度;LSTM神经网络引入门的结构,使其具有长短期记忆功能,能在长时间的计算过程中,保留重要的信息,从而避免长时依赖问题。故针对冷连轧颤振问题,可采用LSTM神经网络模型进行颤振的智能预测。
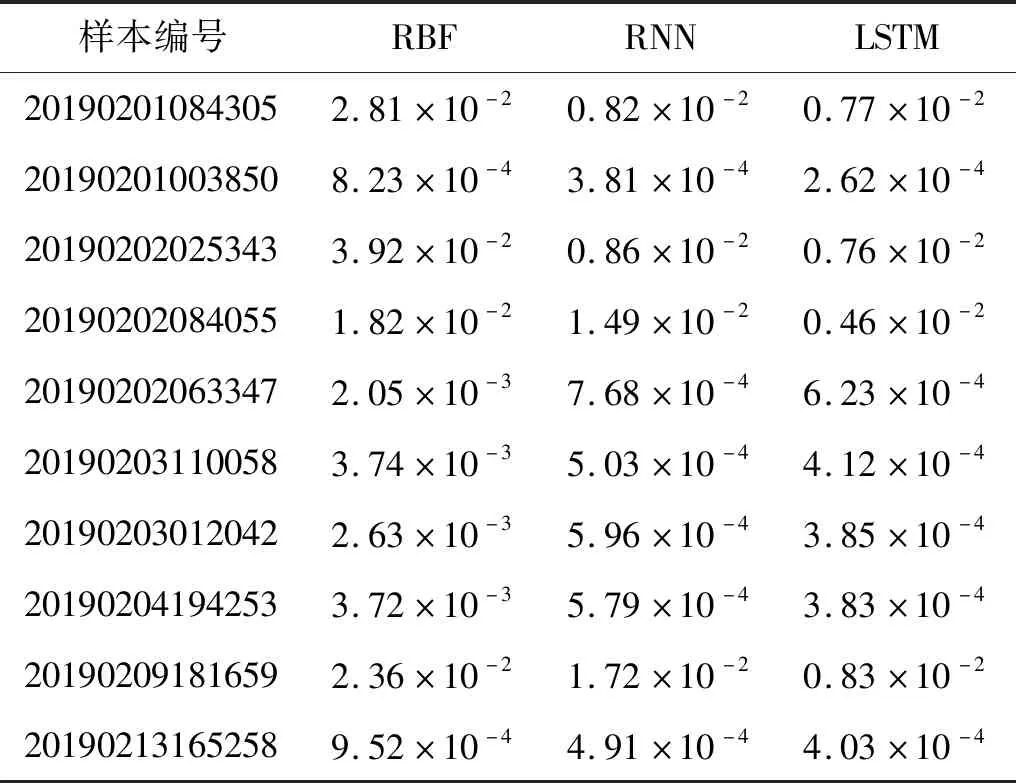
表2 测试数据集的均方误差Tab.2 Mean square error of the test data set
3.3 LSTM神经网络模型预测效果
采用阈值法对轧机振动状态进行识别,通过收集缺陷周期、厚度波动范围等信息,经过统计估计方法得到振动预警线(如图11中虚线所示),当振动能量值低于预警线时,认为轧机系统未发生振动,记为0;当振动能量值超过预警线,认为轧机系统发生振动,记为1。选取四卷振动样本对LSTM神经网络模型的预测效果进行验证,如图11所示,图中模型预测峰值均超过振动预警线,继续对10卷样本进行训练并测试,其振动状态的预测结果如表3所示,均与实际状态一致,故说明LSTM神经网络模型能有效预测颤振的发生。
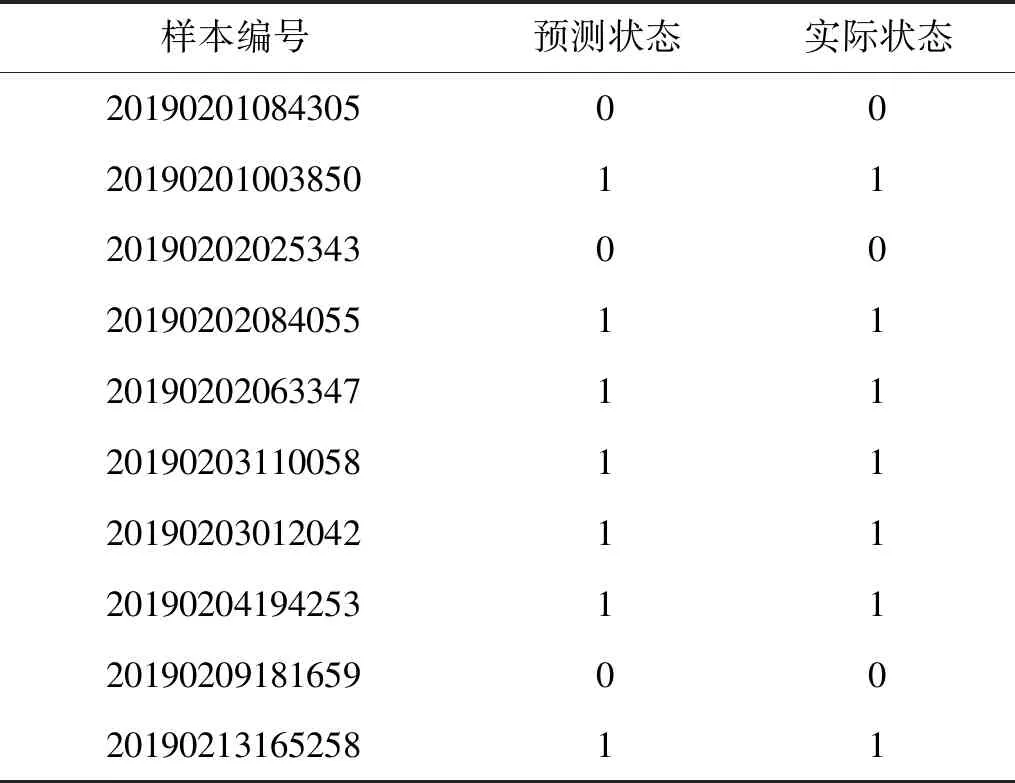
表3 五机架振动状态Tab.3 Vibration state of 5th stand
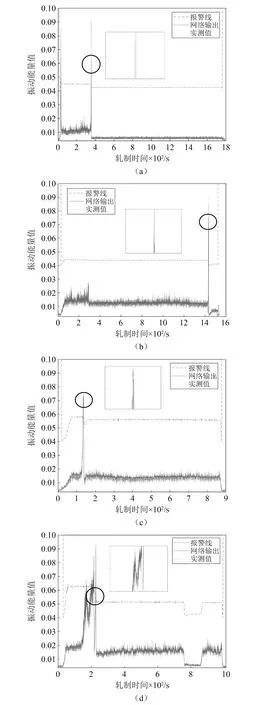
图11 LSTM神经网络训练集及测试集预测效果图Fig.11 Neural network training set and test set prediction performance of vibrating roll
4 结 论
本文以某高速薄板带五机架冷连轧机组为研究对象,针对冷连轧生产过程中的颤振问题,着眼于在工业数据驱动下,通过智能化解决“价值损失”和“决策优化”的问题,实现颤振的智能预测。
(1) 采用函数型数据分析的方法可解决颤振时空大数据在样本构建和特征表征中的尺度差异问题,通过在最小二乘法的拟合标准均方差中加入粗糙惩罚项实现函数光滑甚至导数光滑,使其在处理突变处有更好的效果,增加样本容量的同时提高样本扩充的精度。
(2) 经过SelectKBest特征选择可得,机架前速度、四机架速度等6个特征量与五机架振动能量值具有较强的相关关系,采用这6个特征量作为输入向量来预测五机架振动能量值,可避免其他特征量的干扰,建立精度更高的网络模型。
(3) 基于LSTM神经网络建立预测模型对五机架振动能量值进行预测,并根据测试集的均方误差与RBF、RNN神经网络模型进行比较,发现LSTM神经网络模型对于时序的预测具有较高的精度,同时采用阈值法验证该模型能有效地预测颤振的发生。
