基于无监督学习和粒子滤波的非视距信号检测

侯宁宁,李灯熬,赵菊敏

(1.太原理工大学 信息与计算机学院,太原 030024; 2.山西省空间信息网络工程技术研究中心,太原 030024;3.太原理工大学 大数据学院,太原 030024)

非视距和多径信号是影响全球卫星导航系统(global navigation satellite system,GNSS)定位精度困难大的误差源之一。反射或非视距信号与直接视距信号结合时,会产生不必要的多径效应,仍然是误差的主要来源[1-2]。多径不能通过差分技术去除,从而限制了多径易发区域的定位精度[3-4]。检测和抑制非视距(non line of sight,NLOS)方法主要分为3类:基于天线方面的双极化天线[5],基于接收机方面的先进接收机设计和传感器集成[6],基于导航处理器方面的三维建筑模型[7]。由于现实环境中非视距信号的复杂性,他们都需要外部硬件或最新的地图,这些昂贵的或不实际的大众市场应用程序,仅使用单一的检测方法无法达到满意的效果。

近年来,一些学者提出利用机器学习方法区分非视距信号。文献[8]提出使用支持向量机识别视距/非视距(line of sight/non line of sight,LOS/NLOS)场景。文献[9]提出了一种新的基于有监督机器学习算法的LOS/NLOS分类方法。上述研究都是基于监督学习的GNSS信号分类方法,需事先对学习样本进行标记,因此,需要借助额外的硬件或软件。无监督学习是一种对不含标记的数据建立模型的机器学习方法。文献[10]提出一种无监督机器学习的数据聚类方法,将测量数据分为LOS信号和NLOS信号。文献[11]提出采用“高斯混合模型的期望最大化”的无监督机器学习方法,对LOS和NLOS分量进行分类,但2种方法均应用于室内无线信号,借鉴该思路可以将无监督学习对信号的分类应用于GNSS信号,同时为了解决传统k-means算法对簇中心敏感的问题,使用了核k-means聚类算法,旨在提高GNSS设备在复杂环境下的定位精度,可以避免额外软硬件的使用,提高运算效率。对于定位优化部分,本文提出无监督学习-粒子滤波(unsupervised learning-particle filtering,UL-PF)算法为提高定位精度做2次保障。

聚类是一种无监督的学习分组技术,其提供了一种自动形成相似事物聚类的方法,这就像自动分类[12]。粒子滤波是一种视觉跟踪工具,依赖于蒙特卡罗链框架和贝叶斯估计,适用于非线性和非高斯系统[13]。文献[14]提出采用粒子滤波方法结合行人航位推算算法和磁性指纹图谱有效提高室内定位的精度和效率。文献[15]提出了一种基于遗传算法的简化粒子滤波方法。文献[16]提出了一种改进蒙特卡罗定位算法的概率激光定位方法,通过加入卡尔曼滤波后的GNSS信息来增强粒子权值,从而提高自主车辆定位精度。文献[17]根据粒子的状态值将采样粒子集合的状态空间划分为可变大小的可数测度空间,实验结果表明,在空间域对采样粒子进行简单的启发式划分后,性能有显著的提高。因而可以进一步研究一种挖掘采样粒子空间分布相关信息的有效方法。

对于定位优化部分,本文使用通过聚类算法优化的粒子滤波方法,为提高定位精度做二次保障。首先,提出了一种基于核k-means聚类算法的采样粒子状态空间分割方法,该方法考虑了采样粒子在状态空间分布中的内在相似性。其次,探索在每个聚类中选择一个粒子作为重要粒子,利用时间序列相关技术提高重采样粒子集的多样性。最后,通过伪距残差似然函数有效性检验,证明了该算法重采样的粒子集与原始粒子集来自同一分布。实验结果表明,与传统粒子滤波算法相比,所提算法能获得更准确的估计。

1 GNSS信号核k-means聚类算法

1.1 GNSS信号特征提取分析

使用无监督学习对GNSS信号进行分类的关键是从原始观测数据中提取主要特征。原始数据一般包含伪距、载波相位、载噪比和多普勒频移等,他们都与GNSS信号类型有着密切的联系。而任何单一特征都不可能对GNSS信号进行有效的分类,因此,需要通过不同特征的组合来提高分类的准确性。

1)载噪比。一般来说,LOS载噪比较高,而NLOS载噪比较低。在城市峡谷环境中,经过光滑的建筑物表面反射后,NLOS信号的强度可能与LOS强度相当,这种情况下,仅利用载噪比已经难以将二者区分开来。

2)伪距残差。当观测环境较好时,伪距残差偏大的对应NLOS,但当观测环境不好时,可见卫星少于4颗时,此时的观测方程不再超定,伪距残差为0,不足以作为区分指标。

3)卫星高度角。通常情况下,LOS卫星的高度角较大,而城市峡谷环境中,可见卫星能见度差,LOS卫星被高楼遮挡,卫星高度角也比较大,因此使用卫星高度角可能出现误判,还会破坏卫星的几何分布。

1.2 k-means算法

对于复杂环境下GNSS接收机接收到的卫星信号一般分为LOS、多径和NLOS信号3类,每一类信号都与载噪比、伪距残差和卫星高度角有一定的内在联系。根据这一特性,本文采用核kmeans算法进行信号的聚类,当其中样本离聚类中心最近时,即归为该类。对于给定的一组样本集X={x1,x2,…,xN},xN={rn,vn,en}为标准化载噪比、伪距残差和卫星高度角组成的特征向量,N为样本数,n为样本的特征向量下标,k-means算法将其划分为M个簇C1,C2,…,CM,使得每个数据点与其最近的聚类中心的满足平方欧几里得距离和最小,即

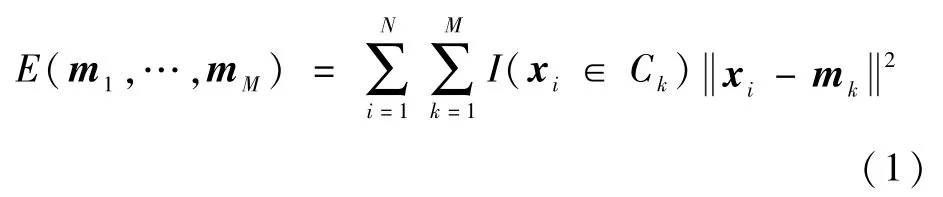
式中:xi为样本,i为样本编号;I为M个簇中选取的样本数据集;k为簇的编号;mk为均值向量,表达式为

k-means算法的缺点是:最终的分类结果取决于集群中心的起始位置,且星团是线性分开的。为了克服这个问题,选择使用核k-means聚类算法[18]。核k-means聚类算法通过使用k-means算法中包含N个数据大小的初始位置的确定性全局,一次动态添加一个聚类中心[19]。

1.3 核k-means聚类算法

1)初始化。在数据集中随机选取K作为初始质心cp,1≤p≤K,p为样本数量,K为数据集的数量。

2)聚类。计算每条记录与质心之间的相似度sim(ri,cp),并将记录ri分配给相似的cp质心。

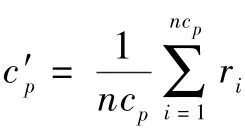
4)终止条件。所有旧质心的矩阵为Θ=[c1,c2,…,cK]T,1≤p≤K,所有新质心的矩阵为Θ′=[c′1,c′2,…,c′K]T,下一步,欧几里得距离为

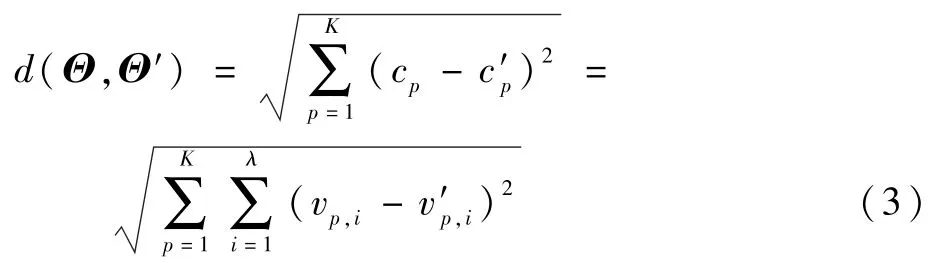
式中:vp,i和v′p,i分别为cp和c′p的质心元素。

核k-means聚类算法是k-means算法的推广,通过非线性变换Φ数据点从空间输入映射到高维特征空间。在k-means算法核中,由于重叠数据在新的维度空间中可以是线性的,因此,期望数据能够很好地分开[18]。

用核k-means聚类算法约简的目标函数等同于特征中的分组误差,如下[19]:

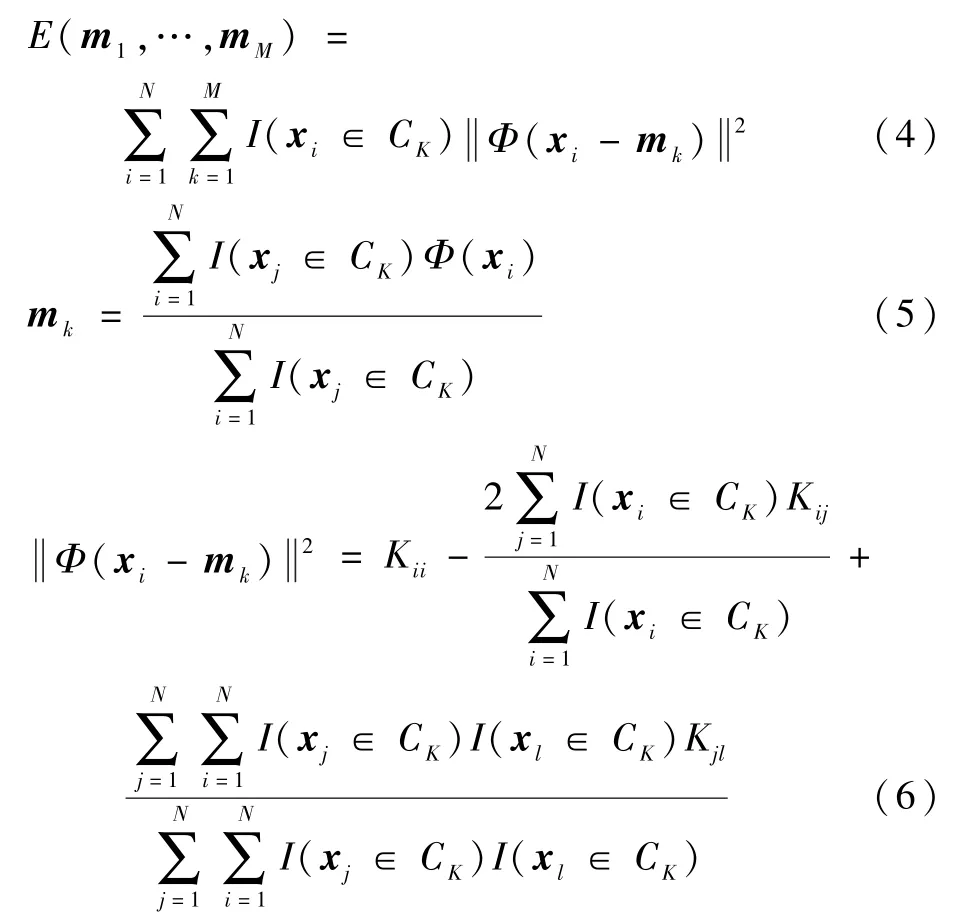
式中:Kii、Kij和Kjl分别为对应样本ii、ij、jl的径向基函数的核函数,本文选择径向基函数(RBF),B-Spline核定义在区间[-1,1]上。由递归公式给出:

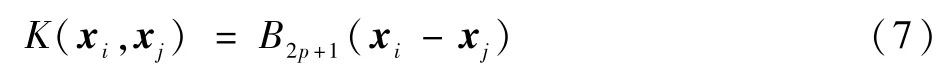
式中:p∈X且Bi+1=B⊗B0,X为样本集,⊗指圈乘运算。得到核函数:

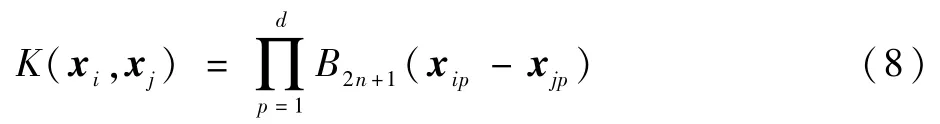
使用径向基函数核k-means聚类算法,通过式(3)～式(8),所有的GNSS信号都被归类到不同的集群,k-fold将样本数据划分为m个部分,复杂环境中GNSS信号通常分为LOS、多径和NLOS共3类,因此选择k-fold=3。由于卫星与终端的距离保持在一定的范围内,LOS环境中同步的峰值信噪比(PSNR)也会相应保持在一个区间内。采用无监督机器学习的数据聚类方法,将实测数据分为LOS、NLOS和多径信号。图1为基于核kmeans聚类算法的GNSS信号的仿真分类结果。图1(a)为分类前只能已知目前存在3种信号,但无法判别和区分,图1(b)为加入特征向量提取后的聚类方法可以识别3种信号分别对应的分类,蓝色为多径,红色为LOS,绿色为NLOS,横轴为伪距残差ρ,纵轴为PSNR。NLOS的PSNR为负值,多径与LOS的PSNR为正值,而且多径的伪距残差大于LOS。结果表明,在二维状态空间中,按一定的度量被分成3个簇。不同的分类结果以不同的颜色显示,可以看到具有特定属性的信号聚类在一起,而不是简单的分割。最后,利用本节所述的信号分类方法,便可见判定卫星信号是LOS还是NLOS传播,需从伪距观测量中剔除该卫星的信号。将受NLOS效应干扰严重的卫星剔除,获得精度更高的伪距观测量,为后续优化定位算法做准备。

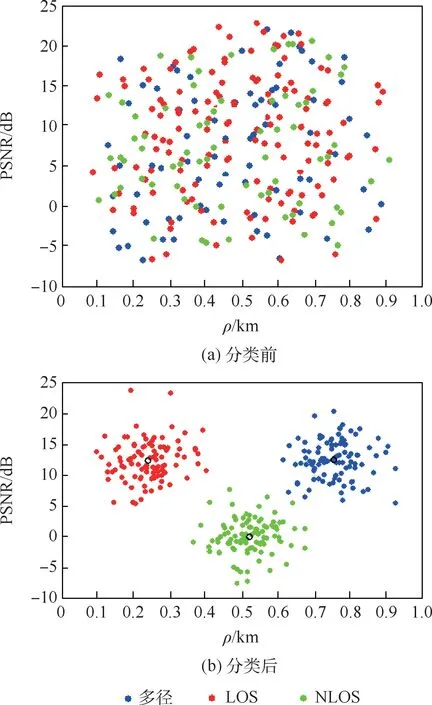
图1 基于核k-means算法的GNSS信号仿真分类结果Fig.1 GNSS signal simulation classification results based on kernel k-means algorithm

2 粒子滤波定位算法

步骤1粒子初始化处理。对GPS接收机输出的原始测量值进行初始化处理,接收机输出的原始伪距集ρ=[ρ1,ρ2,…,ρN]T和经接收机计算得到的参考位置y,用来初始化位置候选点。使用该方法实现位置估计,需要4颗及以上GNSS卫星提供的原始伪距测量值。首先分配位置候选点P(i)=(x(i),y(i)),i为候选点的编号。用随机分布在参考位置的二维高斯分布粒子来表示候选点。在先前的估计位置x(t-Δt)也要放置粒子,t为选取的位置候选点对应的采样时间。在重采样期间,选择正态分布生成粒子,一半粒子的分布为N(y(t),Σ0),Σ0表示正态分布粒子的均值,另一半粒子的分布为N(x(t-Δt),ΣΔt)。在城市环境定位场景中,行人在1s内发生剧烈位置变化的可能性极低,因此,可以利用历元x(t-Δt)的位置信息。

式中:Nsim为经过非视距排除后重新选择的伪距观测量个数。

步骤3评估候选点位置。伪距相似性决定每个候选点的似然函数α(i)(t)(i=1,2,…,NP),似然函数计算如下:

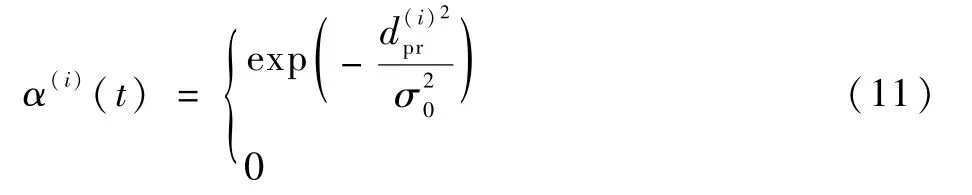
步骤4输出定位结果。对所有有效样本不同时刻位置P(i)(t)加权平均,为最终粒子滤波校正位置提出的方法的定位结果为

3 基于UL-PF算法

本节工作是利用核k-means聚类算法进一步研究采样粒子的空间分布特征,然后在每个聚类中通过时间和序列分析选择一些被称为重要粒子的粒子,以增强重采样粒子的多样性。核kmeans聚类算法通过研究采样粒子的空间分布特征,通过时间和序列分析选择一些重要粒子,以增强粒子滤波重采样粒子的多样性,能够缓解粒子退化,将优化后粒子滤波算法用来后续评估候选点位置,可以提高卫星导航系统的定位精度。

2)使用核k-means聚类算法将候选粒子集划分为带有Np个粒子的聚类gk:

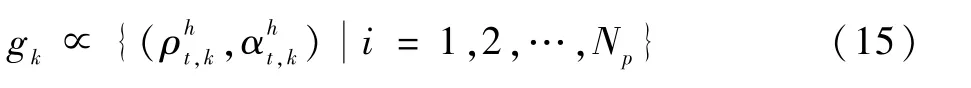
3)选择每个类中下一次筛选的重要粒子:

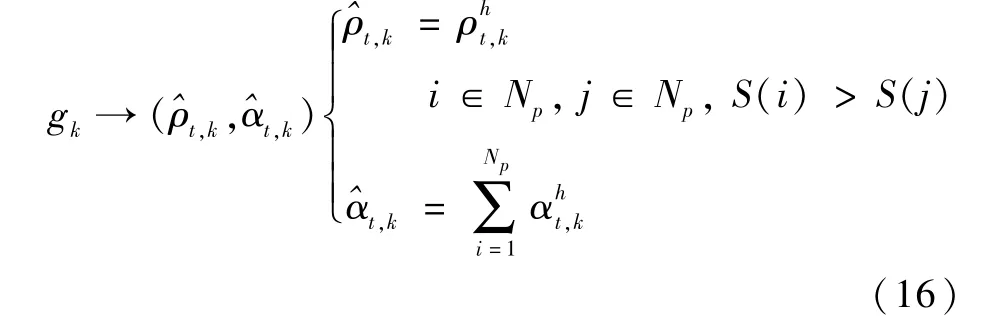
式中:S(i)代表时间序列分析和核k-means选择结果。

4)将第1步中复制的粒子设置为相同的权重:

综上所述,本文的优化定位过程如下:首先,使用北斗卫星导航系统(beidou navigation satellite system,BDS)卫星导航系统的伪距观测量,选择位置候选点和粒子初始化处理,将第2节介绍的GNSS信号分类结果作为NLOS信号检测结果,用来参与后续伪距差的计算;然后,将优化后的粒子滤波器用来优化接收机定位结果,同时,核kmeans聚类算法更新粒子权重用来评估位置候选点;最后,将优化后卫星导航系统的伪距观测量,参与最终的定位结果解算。

4 实验结果

4.1 实验环境

实验过程使用u-blox NEO-M8N GNSS接收器和SIS600B1L1中频采样器采集数据,实验设备如图2(a)、(b)、(d)所示,测试数据的采集地点选择山西太原小店区太航小区,这一区域是城市环境中常见的双侧街道环境,实验环境如图2(c)所示。

图2 实验条件与数据采集Fig.2 Experimental conditions and data acquisition

4.2 定位性能对比

仿真基于BDS卫星的星历数据,行人动态数据集的轨迹图及按照本文算法的信号分类结果如图3所示。图3(a)表示分类前的候选点分布图,图3(b)根据分类结果评估位置候选点,在A、B区域没有受到跨街街道的影响,LOS卫星可见数目较多,由于受到四周高楼遮挡,在C、D、E横街区域接收到NLOS卫星较多。核k-means聚类算法更准确的确认采样点,识别出NLOS卫星,则排除该采样点,从而提高粒子滤波算法定位精度。

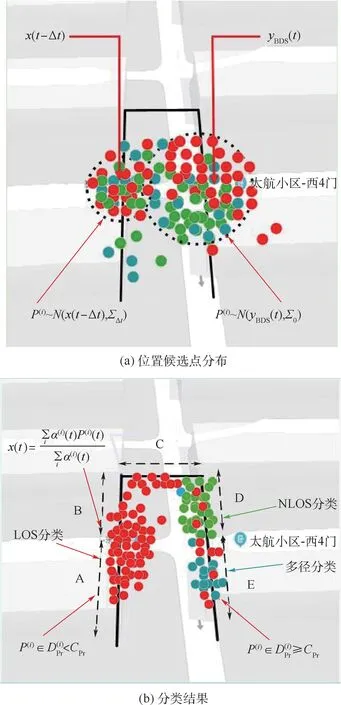
图3 位置候选点分布及分类结果Fig.3 Distribution of location candidate points and classification results

图4为动态场景下定位误差对比。A、B段LOS卫星较多,定位效果较好,A段误差比B段大,是因为A段建筑物周围还有树木遮挡。C、D、E段NLOS卫星较多,未剔除NLOS干扰前误差 甚至高达25m,而且误差曲线不规则不光滑,严重影响定位精度。确定C、D、E段信号分类结果后,将剔除NLOS卫星再进行计算,而剔除NLOS后的误差在5m左右,表明NLOS信号会给定位带来一定程度的系统误差,正确地去除NLOS能够有效地缓解这种系统误差。

图4 动态场景中剔除NLOS前后定位误差Fig.4 Positioning error before and after NLOS elimination in dynamic scene

4.3 算法性能对比

表1给出了核k-means聚类算法与现有的监督机器学习算法、k-最近邻(KNN)、朴素贝叶斯(NB)、决策树(DT)和最小二乘支持向量机(LSSVM)的计算复杂度和性能比较。为简单起见,使用运行时间来度量计算复杂度。仿真中,分别生成500个LOS波形和500个NLOS波形来训练有监督机器学习算法,不同算法的性能对比如表1所示。

表1 不同算法对比Table1 Comparison of different algorithms

从表1中可以看出,无监督机器学习核kmeans聚类算法与有监督机器学习算法相比,在性能上有一定的差异,但由于没有训练阶段,所以不需要训练数据。核k-means聚类算法只需要最先进的监督机器学习LS-SVM所需的44%的运行时间,但其实现了LS-SVM算法几乎相同的NLOS检测准确度。

为进一步证明本文提出的UL-PF算法性能,图5为复杂环境和空旷环境中定位误差。复杂环境中,传统粒子滤波(particle filter,PF)算法定位误差平均值约为6m,UL-PF算法平均值在3m左右,并且波动幅度较小,定位性能较为稳定。空旷环境中,传统粒子滤波算法定位误差平均3m左右,UL-PF算法平均在1.5m左右。

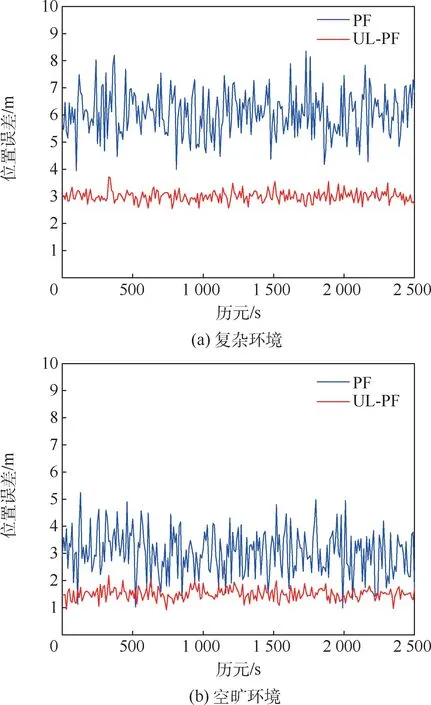
图5 不同环境下本文算法与传统算法定位误差对比Fig.5 Comparison of positioning errors between the proposed algorithm and traditional algorithms in different environments

图6将本文算法与传统算法、PF和扩展卡尔曼滤波(extended Kalman filter,EKF)算法进行对比。图6(a)显示了使用单个LEO卫星的平均定位精度的仿真结果。纵轴表示平均定位精度。测量数据中含有大量的NLOS数据,导致传统算法定位精度较差,收敛时间较长。当测量时间达到350s时,传统方法的精度逐渐收敛到6m左右。与传统算法相比,基于非监督学习NLOS排除的定位方法大大降低了NLOS误差的影响,使定位精度显著提高,收敛时间缩短当测量时间达到200s时,定位精度约为6m;当测量时间达到400s时,定位精度收敛到约3m。

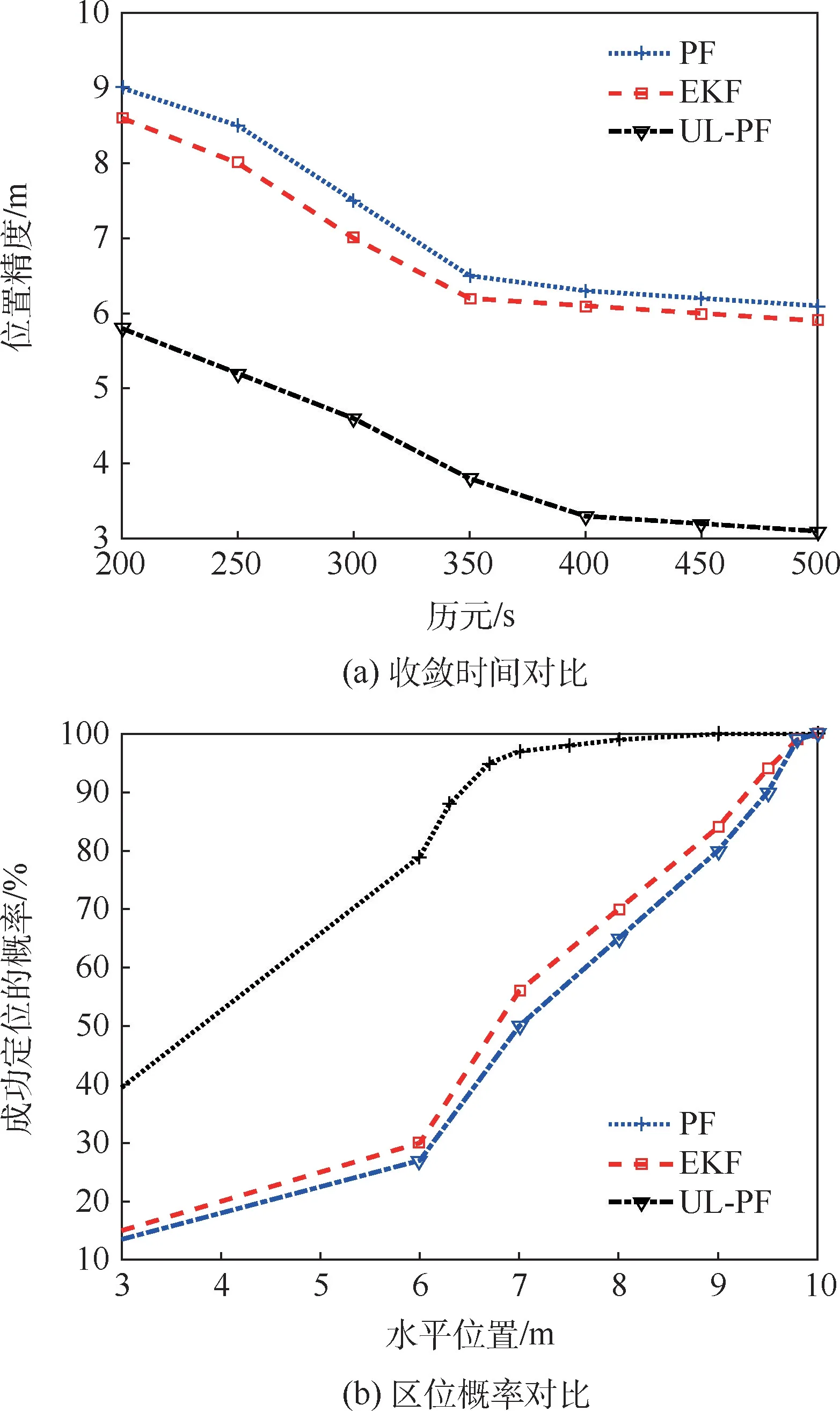
图6 不同算法的收敛时间和区位概率对比Fig.6 Comparison of convergence time and location probability of different algorithms

图6(b)显示了城市场景中的位置概率。由于卫星定位精度和定位成功率与测量误差密切相关,本文算法对测量数据中的非视距信号进行分类排除,可以有效降低非视距信号误差的影响,提高定位成功率。如图6(b)所示,本文算法的成功定位概率明显高于其他2种算法,在定位误差为7m时,定位成功率可达99%,而传统算法在定位误差为10m时,定位成功率可分别达到97%和99%。

5 结 论

针对城市环境中非视距效应问题,本文介绍了一种基于无监督学习和粒子滤波的非视距信号检测方法,进而通过优化的粒子滤波器来优化定位结果,为提高精度提供2次保障。实验结果表明,剔除NLOS信号影响后,能有效提高平均定位精度和缩短算法收敛时间。

1)与传统方法相比,基于非监督学习NLOS排除的终端定位方法定位精度显著提高,收敛时间缩短,当测量时间达到200s时,定位精度约为6m;当测量时间达到400s时,定位精度收敛到约3m。

2)所提方法的成功定位概率明显高于粒子滤波和扩展卡尔曼滤波2种方法,在定位误差为7m时,定位成功率可达99%,而传统方法在定位误差为10m时,定位成功率可分别达到97%和99%。

尽管本文针对缓解NLOS效应已经有一定研究成果,但仍有需要深化和改进的方面。机器学习方法对于不同的数据集场景有着不同的分类效果,本文只采用低速动态的行人数据集进行实验,还需进一步研究接收机处于车辆实时高速动态环境下场景变化对分类效果的影响,此外,针对GNSS信号的载噪比,伪距残差和卫星高度角的样本数据集,还需选择更加合理的特征向量归一化方法。本文所开展的研究具有一定的社会价值,可以应用于驾考系统、智慧城市及无人驾驶等方面,加快城市现代化进程建设。