基于凸优化和LQR的火箭返回轨迹跟踪制导
2022-11-30吴杰张成李淼熊芬芬
吴杰,张成,李淼,熊芬芬,*
(1.北京理工大学 宇航学院,北京 100081; 2.北京特种机电研究所,北京 100012)
可重复使用运载火箭可大幅降低单次发射成本、提高火箭发射密度、降低残骸的危害[1-2],是未来运载技术发展的必然趋势。近年来,随着以美国猎鹰9(Falcon-9)为代表的可重复使用运载火箭的多次成功发射、回收和重复使用,掀起了世界各国对可重复使用运载器的研究热潮。
火箭返回主要包括调姿段、修航段、高空下降段、动力减速段、气动减速段和垂直着陆段[1]。对于调姿段和高空下降段,火箭处于稠密大气层外且发动机关机,通常火箭无制导飞行能力;对于修航段,火箭主要任务是调整航程,飞行轨迹也较为固定[3]。而本文所研究的动力减速段,是指运载器进入大气层后,利用发动机反向点火进行制动减速的飞行阶段。动力减速飞行过程中,要求运载器以一定的速度飞行到预定区域,运载器面临严峻的热流约束、过载约束和动压约束等过程约束;同时运载器动力学具有非线性和高动态等技术特征;此外,为提高可重复使用火箭的运载能力,还要求其再入过程中使用燃料尽可能少。这些都对动力减速段轨迹规划与制导提出了巨大挑战。
标称轨迹跟踪制导方法广泛应用于航天器再入制导,其根据返回器在飞行过程中的端点约束和过程约束形成一条标称轨迹,然后进行在线轨迹跟踪制导。标称轨迹跟踪方法早期主要采用PID控制方法,Harpold和Graves[4]以航天飞机再入返回为应用背景,纵向制导采用PID控制,根据实际飞行状态与标准阻力加速度-速度剖面之间的偏差生成控制指令,但该方法依赖于标称轨迹,不能适应较大的初始误差。近年来,基于现代控制理论的标称轨迹跟踪制导设计方法得到广泛研究。Roenneke和Cornwell[5]针对低升阻比再入飞行器使用基于线性反馈的方法来跟踪轨迹。Dukeman[6]针对航天飞机再入段,采用线性二次调节器(linear quadratic regulator,LQR)方法进行闭环反馈控制,实现对标称轨迹的跟踪,取得了良好的跟踪性能。张大元等[7]针对防空导弹弹道跟踪问题,利用LQR理论设计弹道跟踪制导律并验证存在初始误差和风干扰下的跟踪效果。刘晓东等[8]、宋晨等[9]研究了自适应动态面标称轨迹跟踪方法,该方法同样具有良好的跟踪性能。但是,这些方法一般都是以对轨迹进行高精度跟踪,即位置跟踪偏差最小作为最优控制目标,无法考虑燃料最省。而且,即便在基准轨迹的设计过程中考虑了燃料最省,但是在火箭返回过程中面临着各种复杂干扰和模型的强不确定性,轨迹跟踪中必然需要消耗额外的燃料。因此,需要在轨迹跟踪中对燃料消耗进行重规划,以期达到尽可能减少燃料消耗的目的。此外,基于LQR的轨迹跟踪方法需要提供精确的基准控制输入才能保证较好的跟踪效果,而这在实际中很多情况下难以保证。
近年来,Acikmese和Blackmore等[10-12]成功采用凸优化方法求解火星软着陆制导问题,引发了基于优化的制导算法的技术创新。由于凸优化具有计算效率高的特点,且能有效处理过程、终端等各类约束,在飞行器轨迹优化和制导中得到越来越多的应用。Liu和Lu[13]提出序列凸化方法将非线性最优控制问题转化为二阶锥规划问题,并成功应用于航天器交会对接[14]等问题。Wang和Grant[15]同样采用序列凸优化算法解决高超声速飞行器再入问题,该方法采取离线轨迹优化,无法实现在线制导。路钊[16]将序列凸优化与滚动时域控制结合,形成了所谓的滚动序列凸优化方法,实现了在线轨迹跟踪制导。序列凸优化方法由于不需要对最优控制问题进行前期繁杂的模型变换、凸化处理,通用性较强,是目前求解非凸最优控制问题的主要方法。但是,该方法的最优解较为依赖模型的具体形式,当动力学系统涉及复杂非线性气动力、状态量变量维数较高时,存在迭代次数多甚至难以收敛的问题,由于计算量较大、可靠性较差,难以适应当前箭载计算机的计算能力,无法满足在线制导的要求[17]。
综上可知,基于滚动序列凸优化方法的轨迹跟踪方法由于集成了凸优化方法,显然能方便地实现燃料最省的要求,但是极有可能存在计算量过大、可靠性无法保证,而无法满足在线制导要求的问题。为了提高滚动凸优化方法的计算效率和求解可靠性,同时追求燃料最省,本文提出一种分段序列凸优化和LQR的轨迹跟踪方法;相比于传统的LQR跟踪制导方法,能有效减少燃料消耗,且可保证具有较高的轨迹跟踪精度和较强的抗干扰能力;相比于现有的滚动凸优化方法,可显著降低计算量、提高方法可靠性。本文提出的轨迹跟踪方法充分利用分段凸优化方法能进行在线优化的优势以实现燃料最省,同时利用LQR具有良好轨迹跟踪性能的优势实现高精度的轨迹跟踪,且无需提供精确的基准推力控制输入,实际使用更加灵活。通过将火箭的运动分解为包含速度和位置相关的两部分,在此基础上利用分段凸优化方法实现火箭的速度跟踪,同时达到燃料最省的目的;利用LQR实现火箭的飞行轨迹跟踪。对于速度跟踪,由于仅包含速度相关的状态量,动力学模型维度降低,凸优化方法求解的效率可大为提升。同时,为进一步降低凸优化方法计算量,在每一个轨迹分段仅求解当前轨迹分段内的最优控制问题,并非从当前分段到飞行终端的整个时域。
1 火箭运动方程
考虑到动力减速段火箭始终保持尾部向前飞行,速度方向不发生改变,将火箭箭体坐标系定义为x轴指向箭体尾部,火箭所受的空气动力均建立在此坐标系中。火箭纵向平面几何关系如图1所示,其中O′为火箭质心位置。
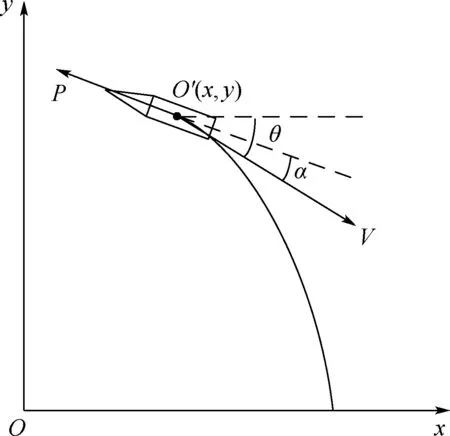
图1 火箭纵向平面几何关系Fig.1 Geometric diagram of rockets in longitudinal plane
运载火箭动力减速段飞行航程一般在100km左右,因此可以忽略地球自转;火箭飞行高度一般在20~70km之间,重力加速度可简化为常值。将火箭质心运动方程建立在发射坐标系内,纵向平面内的火箭再入运动方程如下:
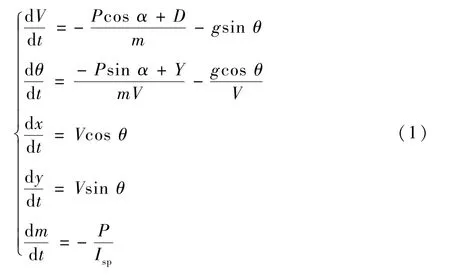
式中:V为火箭飞行速度;θ为速度倾角;x、y分别为火箭飞行位置的横、纵坐标;m为火箭质量;D为火箭所受阻力;Y为升力;Isp为发动机比冲;α为攻角;P为火箭的推力;g为重力加速度。D和Y分别表示为

式中:Sref为参考面积;Ca为阻力系数;为升力系数关于攻角α的导数,本文将气动升力视作攻角α的线性函数;ρ为大气密度,可以表示为

式中:ρ0=1.225kg/m3为海拔为0时的空气密度;h=7254.3m。
轨迹跟踪的核心是对位置的精确跟踪,而对实际飞行时间和标称轨迹对应的飞行时间之间的差异不作要求,因此无需一定采用时间为自变量。如果取火箭的航程或高度为自变量,不仅可保证对位置的精确跟踪,而且在凸优化方法的应用中无需优化飞行时间(火箭飞行至预定点的时间无法提前确定),从而可降低系统状态变量的维数,提高计算效率和可靠性。因此,在式(1)的基础上,选择火箭位置x坐标为自变量,得到新的火箭运动方程如下:
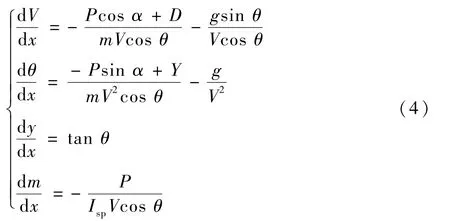
式中:关于速度倾角θ的有些项出现在分母中,当θ=90°时会出现奇异的情况。然而,可重复使用运载火箭返回过程在动力减速段之后还有气动减速段和垂直着陆段,因此在动力减速段速度倾角一般不会大于70°,该模型可以应用于火箭动力减速段。
2 轨迹跟踪制导律设计
2.1 轨迹跟踪制导策略
获取一条基准轨迹,获取基准轨迹的方法不限,但要保证基准轨迹满足过程约束、终端约束,这样才能让火箭顺利完成动力减速段的制导任务。为了保证火箭返回过程中满足各种约束及使用燃料最少的要求,基准轨迹的获取可采用基于凸优化或高斯伪谱法[18-19]的轨迹规划方法。
基准轨迹确定后,轨迹跟踪制导采用速度跟踪和位置跟踪独立设计的制导方案,基于LQR的位置跟踪制导确保对轨迹位置的高精度跟踪,通过不断修正过载控制量,减少轨迹位置偏差;基于分段凸优化方法的速度跟踪采用分段跟踪策略,每个轨迹分段采用凸优方法化求解最优控制问题,通过对始/末端速度施加约束以实现跟踪,确保火箭在存在初始速度误差和模型误差的情况下,实现对速度的高精度跟踪,同时追求燃料最省。
2.2 基于分段凸优化的速度跟踪
对于速度跟踪制导律设计,为减少凸优化方法的计算量,将速度跟踪按基准轨迹进行分段,滚动时域控制中控制变量的优化只需保证对当前跟踪段上的速度跟踪,而不需要保证从当前分段到飞行结束的整个全程的速度跟踪,从而大幅度降低凸优化的计算时间。具体来说,首先将基准轨迹按坐标x分成M段,可获取M段分段轨迹和(M+1)个分段点,所有的分段点将作为速度跟踪的基准点,在每一分段上的基准点处施加速度相关的初始约束与终端约束。可对x采用均匀分段,也可根据实际情况进行不均匀分段,比如采用类似伪谱法的节点配置方式[20]。本文通过大量测试发现,均匀分段与非均匀分段方法精度相差不大,而前者实现起来更加简单直接,因此本文采用均匀分段的方法。
采用序列凸优化方法求解第j(1≤j≤M)个轨迹分段内的最优控制问题,考虑燃料最省的性能指标,及该段内基准点处初始与终端约束以保证速度跟踪的精度,得到该段的最优控制量即推力P。同时,将推力迅速作用到该分段上,预测该段终端位置处的状态,并根据实际环境考虑各种干扰和不确定性,进行状态更新,将其作为下一个轨迹分段j+1的初始状态,进行下一个轨迹分段上的凸优化求解,直至达到整个飞行轨迹的终点。通过这种分段凸优化的形式,在系统受到各种外界干扰和存在模型误差情况下,也能及时进行修正,不会产生误差积累,确保速度的高精度跟踪。
当考虑对速度进行跟踪时,仅考虑火箭速度和质量的变化如下:

式中:f1和f2分别为速度V和质量m对x的微分;方程左端的变量θ、阻力D取标称轨迹值。由于α较小,可取cosα=1。
对非线性动力学等式约束式(5)进行凸优化,为书写方便将式(5)简写为
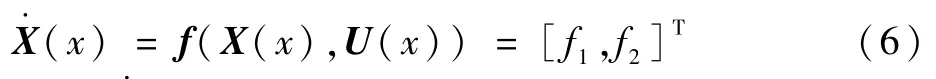
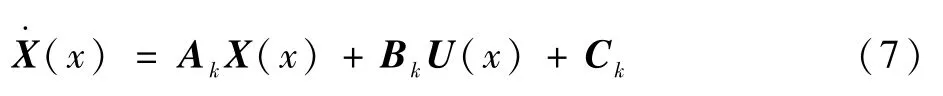
式中:各项系数矩阵中的下角标k表示在第k次迭代对应的参考轨迹处取值,各项系数矩阵可分别表示为
在式(7)的基础上,进一步进行离散化。欧拉离散法[16-17]形式简单、精度足够,在最优控制问题求解中广为采用,本文选用欧拉法进行离散。若需进一步提高精度,也可考虑梯形[21]或伪谱离散法[22]。设离散周期为T,离散点数为N,则状态方程离散为
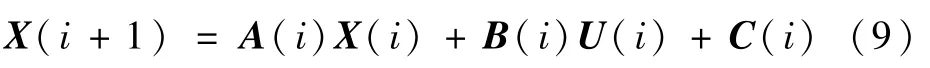
式中:A(i)=TAk+I2,I2为2×2的单位矩阵;B(i)=TBk;C(i)=TCk;i为第i个离散点。
通过加入该段基准轨迹点对应的速度相关的初始约束与终端约束,实现对该分段内的速度跟踪。对于第j个分段,加入始端约束为

式中:下标“0”表示该段的始端约束;下标“f”表示上一分段的速度终值,即始端约束的状态取上一段的终值,而不是基准弹道对应的值,从而实现状态的更新。终端约束为

式中:下标“Bf”为该分段末端基准轨迹对应的速度终值;e1为允许的终端误差,引入e1将终端速度约束设定到一个区域,而非一个点,可提高凸优化求解的可靠性。另外,控制量推力Pi存在幅值约束:

式中:N为每个分段的离散点数。式(13)的含义是使离散控制量的平方和最小,即最小化每个分段燃料消耗。
经过凸化和离散化处理后,得到第j个分段的二阶锥规划问题如下:

式(14)中的凸优化问题由于仅涉及2个状态量和一个控制量,无需对模型进行繁琐的变换和凸化剪裁,且优化时域较短,可采用序列凸优化[23]进行快速求解,提高了凸优化求解的速度与可靠性。
2.3 基于LQR的轨迹跟踪

轨迹跟踪时考虑如下运动方程:
运载火箭等飞行器一般会安装惯性测量装置,可以对火箭受到的加速度进行直接测量,因此选用侧向加速度作为控制变量。火箭侧向加速度可表示为

由式(16)可得火箭运动方程为

式中:f3和f4分别为速度倾角θ和高度y对x的微分。

取扰动系统状态变量Y=[ΔθΔy]T,其中:
式中:下标“B”表示基准轨迹参数。采用小扰动法对动力学方程进行线性化,可得到状态方程为
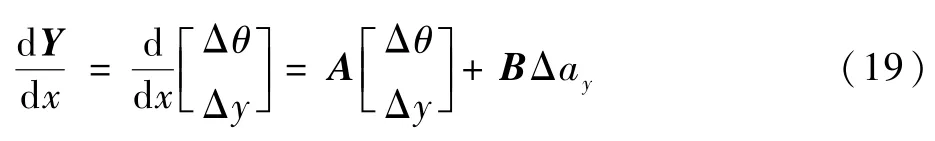
式中:Δay=ay-ayB为控制量。矩阵A、B的表达式为
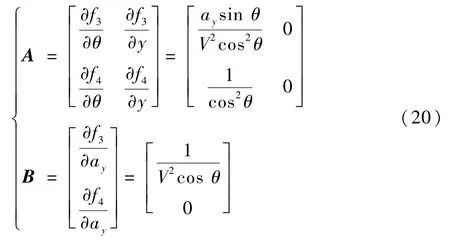
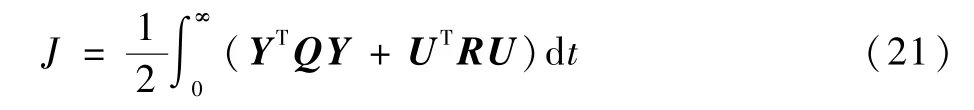
根据LQR理论,对线性系统选定拉格朗日型性能指标如下:式中:Q和R为需要设计的权重矩阵,且满足Q半正定,R正定;Y为系统状态变量。根据LQR理论,如果该系统受到外界干扰而偏离基准状态,则应施加控制量U=-K*Y使系统回到基准状态附近并同时满足J最小,且反馈系数K*为

式中:P为黎卡提方程的解。黎卡提方程可以表示为
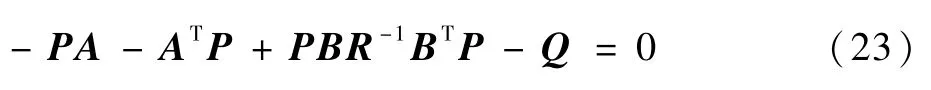
当黎卡提方程无解时,一般可取上一步制导周期的解,这样既可以保证算法的工程实用性,同时也不会影响算法的使用性能。
基于LQR的位置跟踪制导律工作流程,首先,在基准轨迹上按坐标x等间隔取样,按照式(19)获取火箭侧向扰动运动的线性化模型;然后,选择权重指标,计算最优反馈系数矩阵K*;最后,根据实际飞行的系统状态偏差计算控制量U=-K*Y,通过数值积分手段对位置状态方程进行预测,积分步长为Δx。
本文方法的信息流程如图2所示。

图2 本文方法的轨迹跟踪信息流程Fig.2 Information flow chart of trajectory tracking with the proposed method
3 仿真验证
3.1 本文方法与滚动凸优化方法的仿真对比分析
以某运载火箭动力减速段为例进行仿真,火箭初始状态和终端状态如表1所示。基于分段凸优化的速度跟踪由于计算量相较于解析式的LQR大,其制导周期一般更长。本文方法仿真中速度跟踪分段数取10,按x坐标均匀分段,则制导周期为1/10的总横向航程;在每个速度跟踪周期内,分段凸优化先规划出该段内的推力曲线,基于此对式(5)中的速度进行预测;LQR跟踪器计算出控制量ay,然后对位置方程(17)中的位置(y,θ)进行预测。由于LQR解析计算速度非常快,仿真中其制导周期取为每个凸优化速度跟踪制导周期的1/200(按x坐标进行等分)。为了比较公平,基于直接滚动凸优化方法全程同样取10个制导周期。仿真所使用电脑配置为i58400 CPU、8GB内存的普通台式机上。

表1 火箭初始状态和终端状态Table1 Initial and terminal states of rocket
2种方法的轨迹曲线如图3所示。本文方法的基准轨迹是一条离线优化轨迹,在仿真过程中,由于没有考虑外界的各种干扰因素,采用本文方法的飞行轨迹应与滚动凸优化方法的轨迹基本重合,图3的仿真结果也验证了这一点。
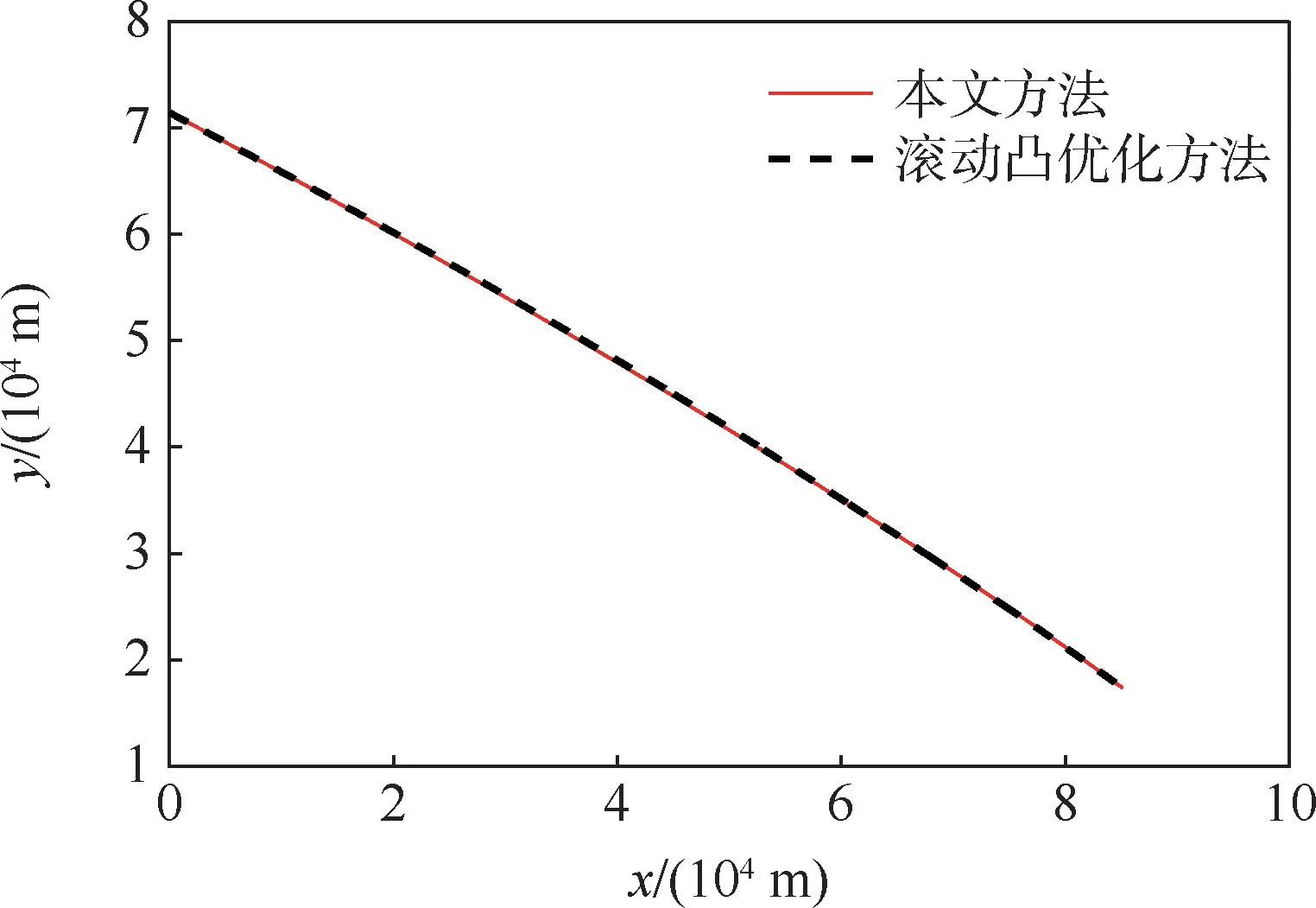
图3 轨迹曲线Fig.3 Trajectory curves
2种方法的计算时间如表2所示。从中可以看出,本文方法的轨迹跟踪制导方法凸优化求解时间为22.66s,远小于滚动凸优化方法的计算时间103.95s。本文方法由于将轨迹跟踪问题简化为速度跟踪和位置跟踪2部分,位置跟踪采用高效率的LQR跟踪方法,速度跟踪形成的最优控制问题由于只涉及到2个状态变量和1个控制量,并采用分段控制策略,计算时间大幅减少。由仿真验证可见,本文方法相比于滚动凸优化方法可大幅度减低计算量。

表2 两种方法的计算时间Table2 Computation time of two methods
在仿真过程中发现,直接采用滚动凸优化方法在求解时容易出现无解的情况。这主要是火箭返回问题涉及的模型状态量和控制量多,过程约束较多且较为苛刻,动力学高度非线性,现有的滚动凸优化方法利用逐次逼近的方法对整个非线性动力学方程线性化,极有可能导致凸化后的问题可行域非常小,实际使用过程中会出现无解的情况,可靠性难以保证。通过引入变量变换、松弛等方法对模型进行凸化和裁剪,可以明显改善凸优化求解的性能,提高可靠性,但凸优化方法针对不同的问题需要专门研究,这对工程人员数学基础和凸优化经验要求较高,通用性与工程适用性较差。而采用本文所提方法,速度跟踪的最优控制问题中系统状态量和控制量减少,且采用分段控制策略可以减少每次凸优化求解中离散点个数,因此该方法在仿真过程中未出现无解的情况,具有更高的可靠性。
综上所述,本文方法在计算速度、求解可靠性等方面明显优于滚动凸优化方法。
3.2 本文方法与LQR方法的仿真对比分析
本节主要从考虑初始误差和同时考虑各种干扰误差2种情况对LQR方法和本文方法进行仿真对比分析,重点分析2种方法的跟踪精度和燃料耗损性能。针对火箭返回运动的强非线性特性,为了减少LQR线性化引起的模型误差,在以下仿真过程中,LQR方法跟踪的基准弹道离散点数取2000个点。
3.2.1 考虑初始误差的轨迹跟踪仿真
火箭初始误差主要包括初始速度误差(ΔV0)、速度倾角误差(Δθ0)及高度误差(Δy0)等,考虑初始速度、速度倾角和高度分别存在+100m/s、+2°和+1000m的初始误差。在相同的场景及参数设置下,分别采用传统的LQR方法和本文方法进行轨迹跟踪制导仿真。
考虑ΔV0下的仿真结果如图4~图6所示。可以看出,2种跟踪方法的跟踪精度基本相当,速度误差在最初始段均得以迅速消除;本文方法速度倾角跟踪误差全程小于0.05°,高度跟踪误差全程小于17m。

图4 速度误差曲线(考虑ΔV0)Fig.4 Velocity error curves(withΔV0)
从图5和图6中可见,本文方法高度跟踪误差和速度倾角跟踪误差出现小幅周期性振荡,这是由于对速度采用分段跟踪,每段只跟踪该段的速度终值,而对中间过程的速度不进行精确的跟踪,因此在端点之间会产生一定的速度偏差,而位置回路会使用速度回路传递的速度量信息,因此会造成速度倾角和高度跟踪误差小幅振荡,但振荡幅度很小,能保证较高的跟踪精度。
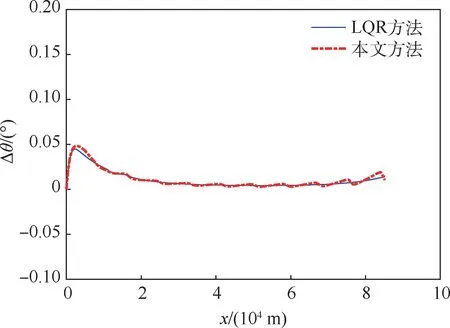
图5 速度倾角误差曲线(考虑ΔV0)Fig.5 Flight path angle error curves(withΔV0)
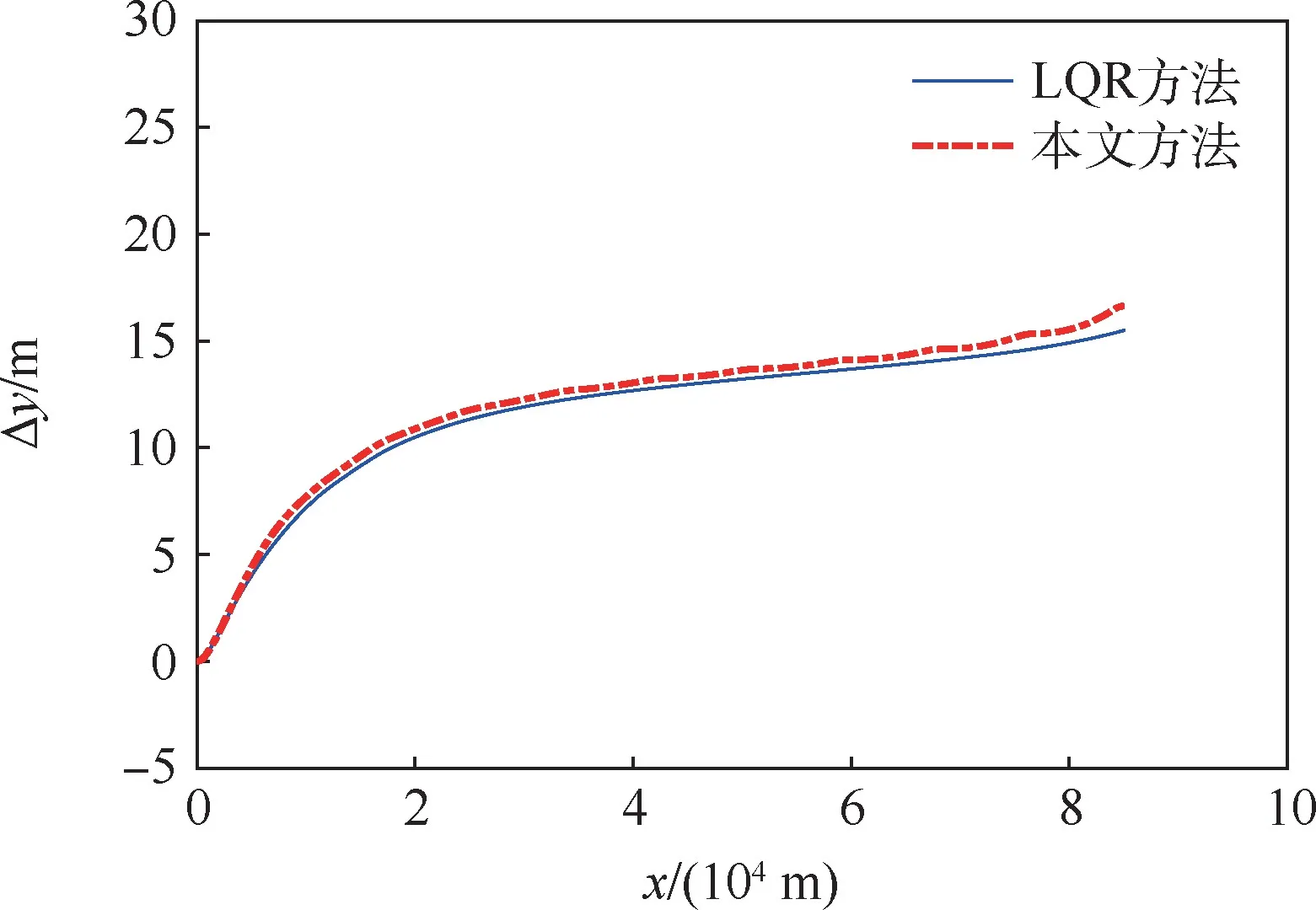
图6 高度误差曲线(考虑ΔV0)Fig.6 Altitude error curves(withΔV0)
考虑Δθ0下的仿真结果如图7~图9所示。可以看出,2种跟踪方法的跟踪精度基本相当,速度倾角误差在飞行过程中逐渐得以消除并很快收敛到0;本文方法在速度跟踪点上误差均小于1m/s,高度误差由于受到初始速度倾角误差的影响逐渐增大,但随着速度倾角偏差的修正,高度跟踪误差也得到进一步修正,初始速度倾角误差消除之后全程高度误差不超过18m。
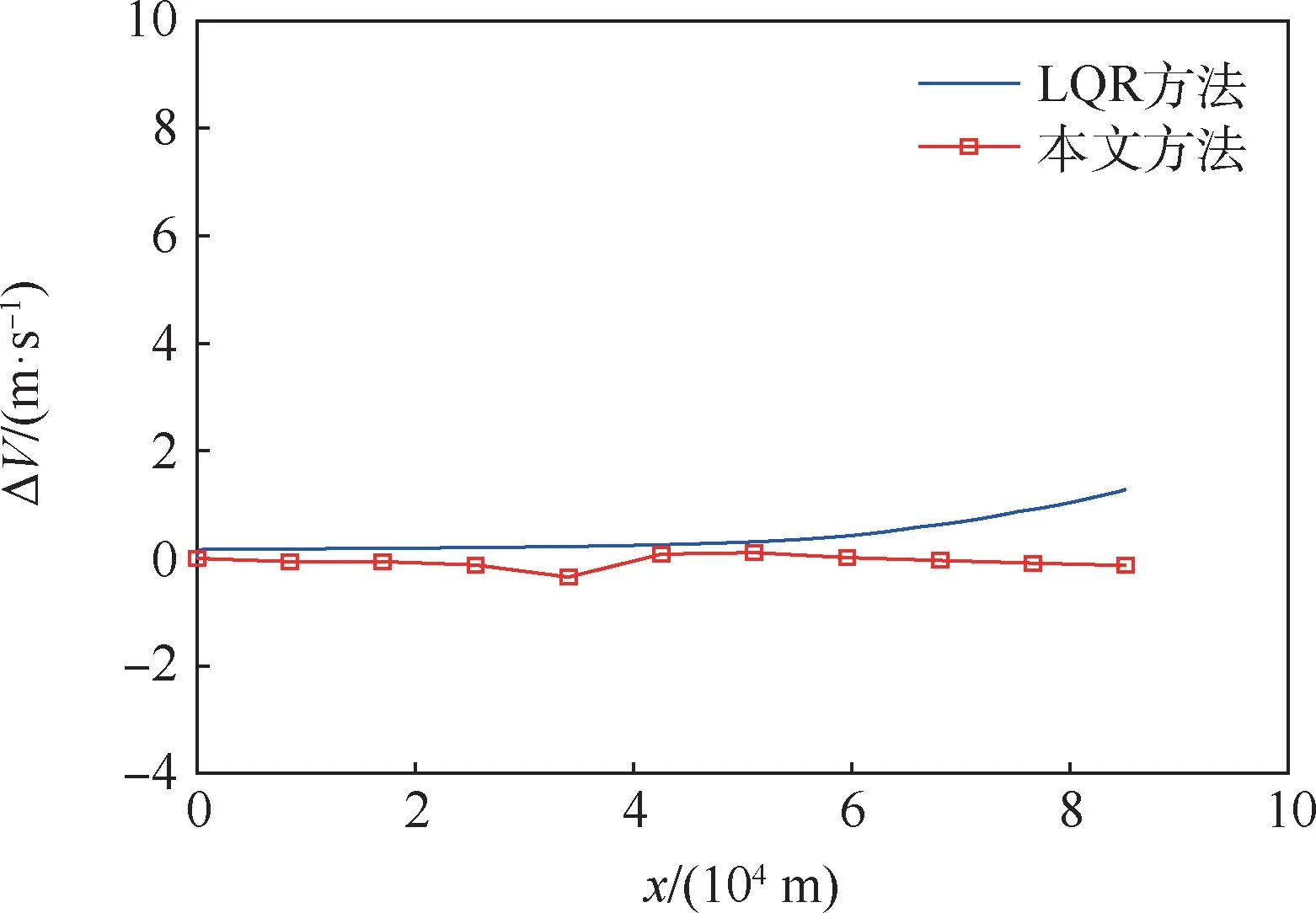
图7 速度误差曲线(考虑Δθ0)Fig.7 Velocity error curves(withΔθ0)
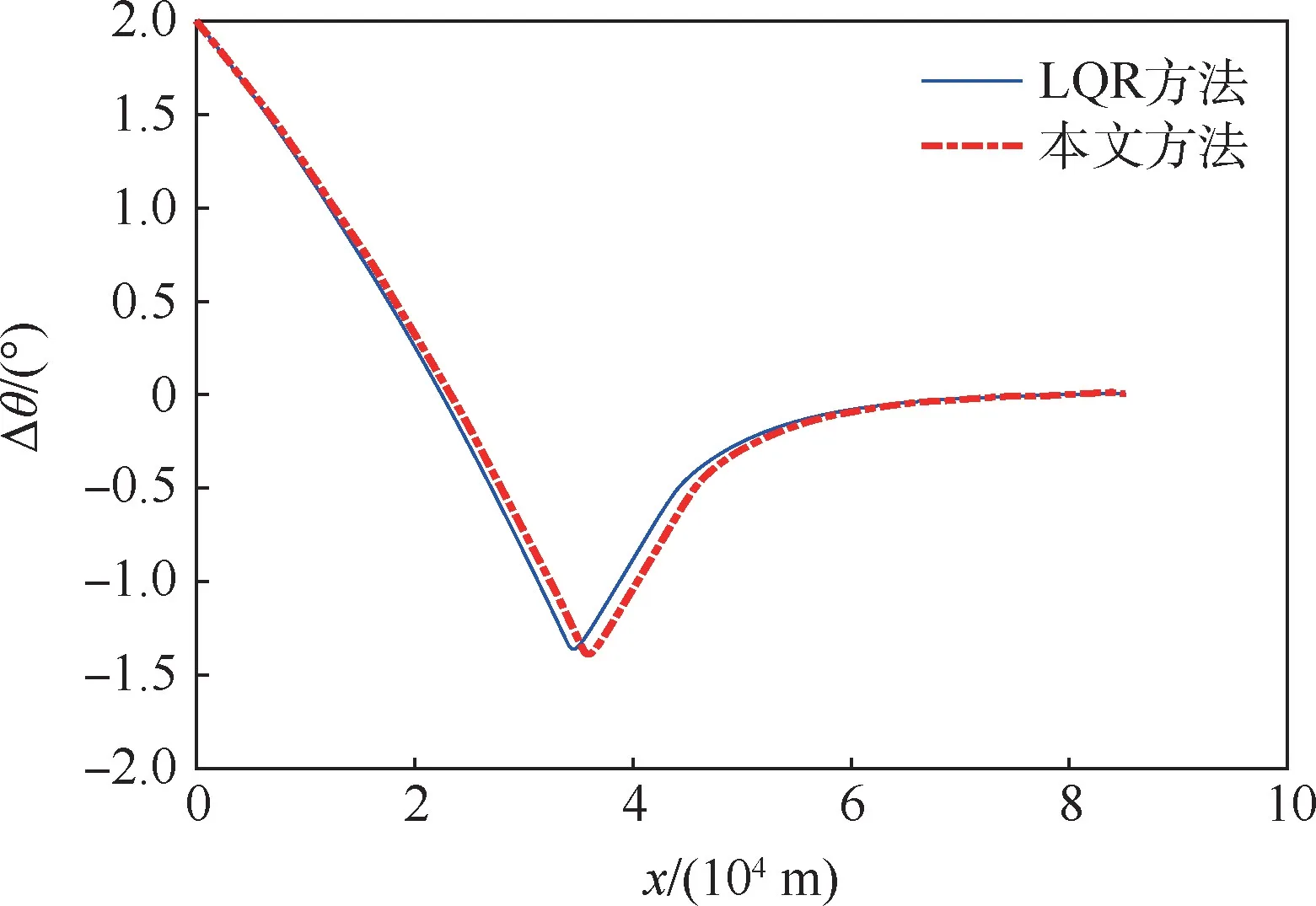
图8 速度倾角误差曲线(考虑Δθ0)Fig.8 Flight path angle error curves(withΔθ0)
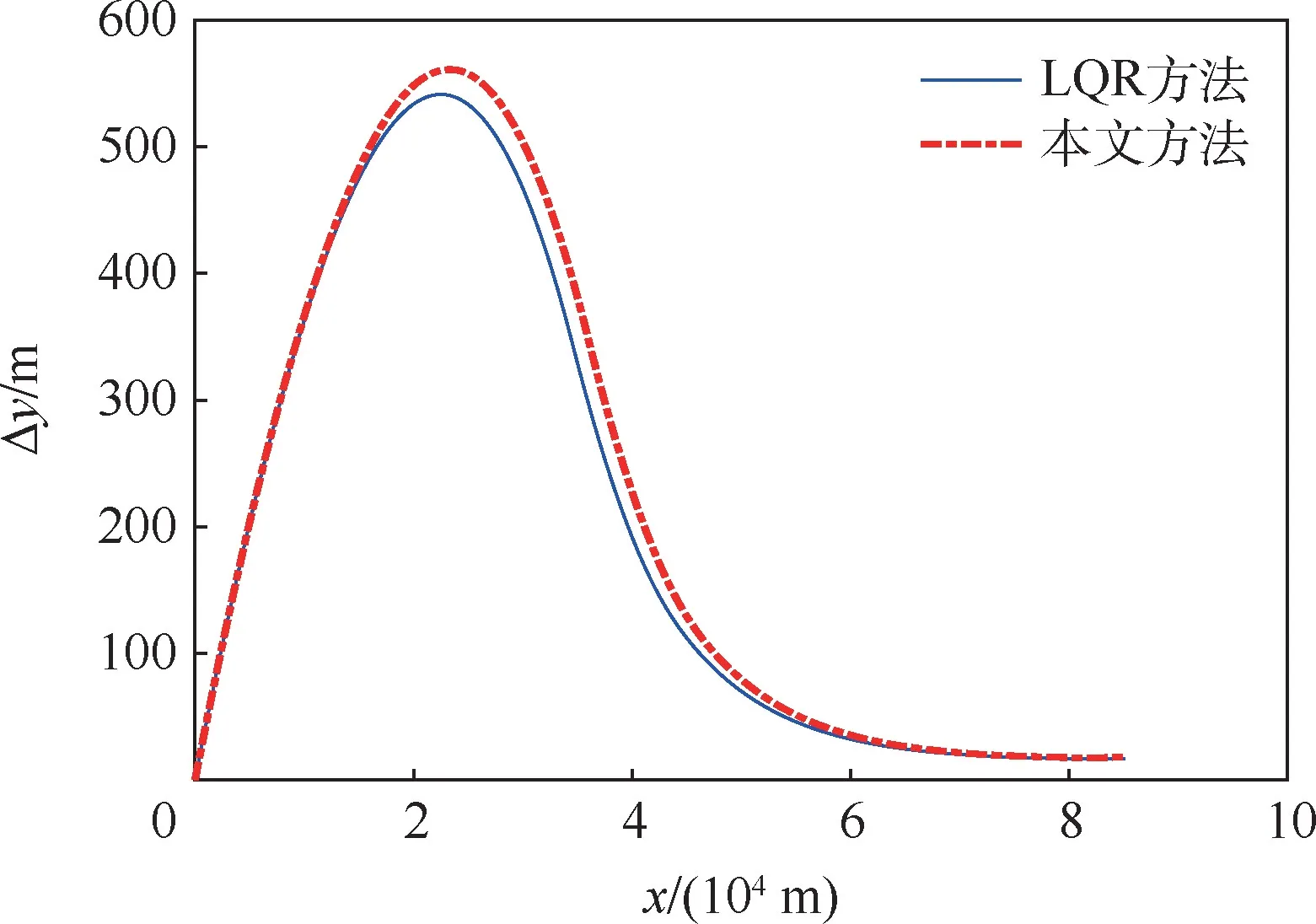
图9 高度误差曲线(考虑Δθ0)Fig.9 Altitude error curves(withΔθ0)
考虑初始高度误差下的仿真结果如图10~图12所示。可以看出,2种跟踪方法的跟踪精度基本相当,本文方法在速度跟踪点上最大误差不超过1m/s,由于初始高度误差的影响,速度倾角跟踪误差先增大后逐渐收敛于0,高度跟踪误差迅速减小,之后全程高度误差不超过17m。
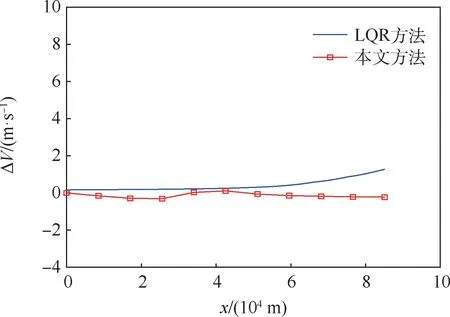
图10 速度误差曲线(考虑Δy0)Fig.10 Velocity error curves(withΔy0)

图11 速度倾角误差曲线(考虑Δy0)Fig.11 Flight path angle error curves(withΔy0)
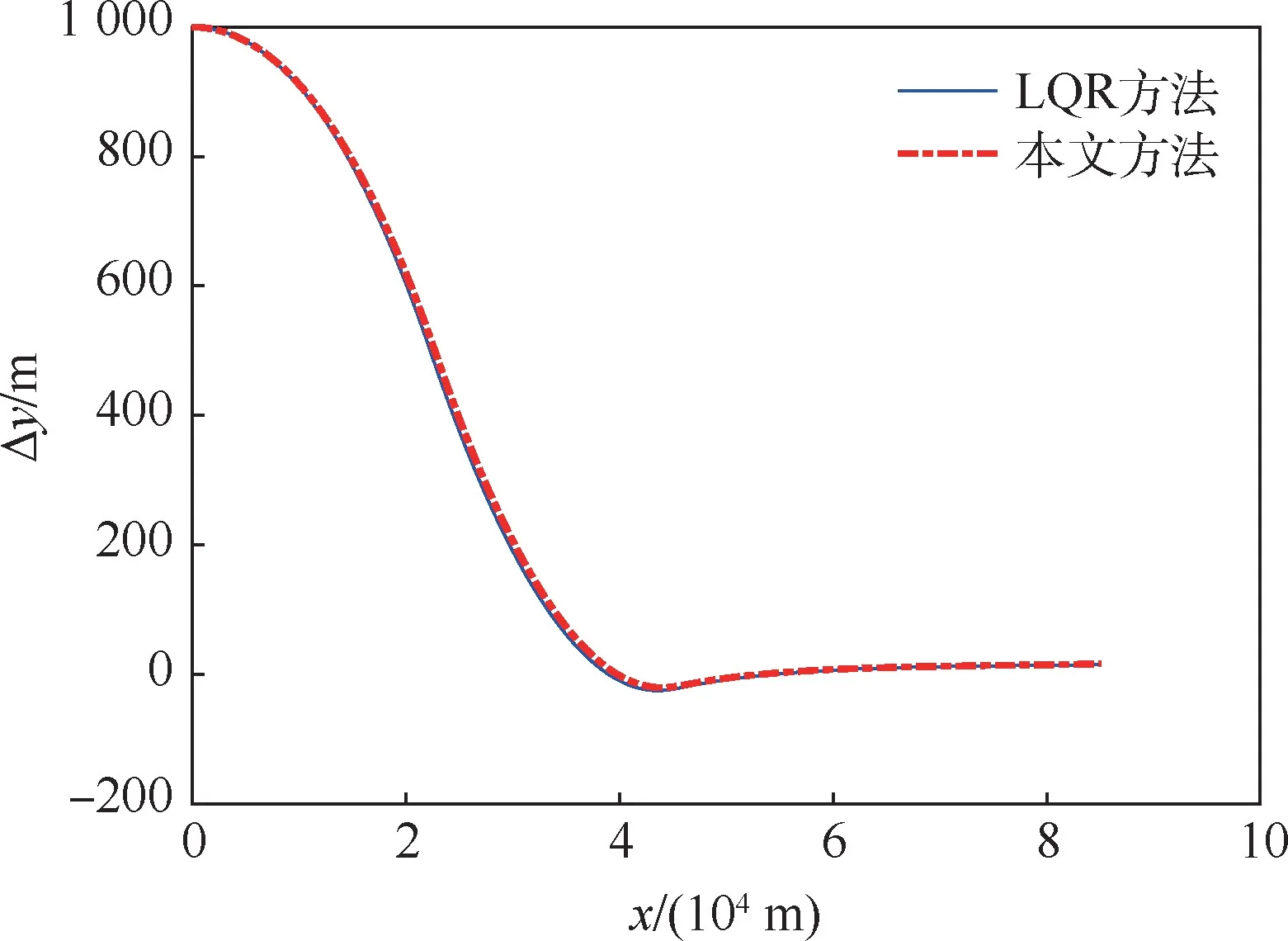
图12 高度误差曲线(考虑Δy0)Fig.12 Altitude error curves(withΔy0)
各种初始误差下采用2种方法的火箭终端剩余质量如表3所示。可以看出,本文方法火箭的终端质量高于传统的LQR方法,终端质量提升268~272kg,燃料更省。
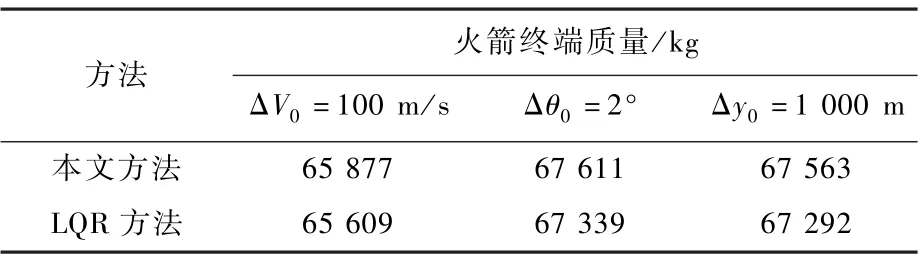
表3 不同初始条件下火箭终端质量Table3 Terminal mass of the rocket under different intial conditions
考虑到动力减速段火箭飞行高度在20~70km之间,空气相对比较稀薄,不能充分发挥气动减速效应达到降低使用燃料的目的,对于更稠密大气层内的轨迹跟踪其节省的燃料将更为可观。
从本节仿真结果可以看出,2种方法的跟踪精度基本相当,而本文方法的轨迹跟踪制导方法可以在保证较好跟踪的情况下降低燃料消耗,且无需提供精确的推力控制输入,使用更加灵活。
3.2.2 考虑各种干扰误差的蒙特卡罗仿真
3.2.1节仿真都是考虑单一的偏差因素,有必要综合考虑各种误差因素同时作用下的轨迹跟踪性能。同时考虑火箭初始状态误差、气动模型误差、风等因素的干扰,各种干扰因素、大小和分布形式如表4所示,采用蒙特卡罗方法进行仿真。
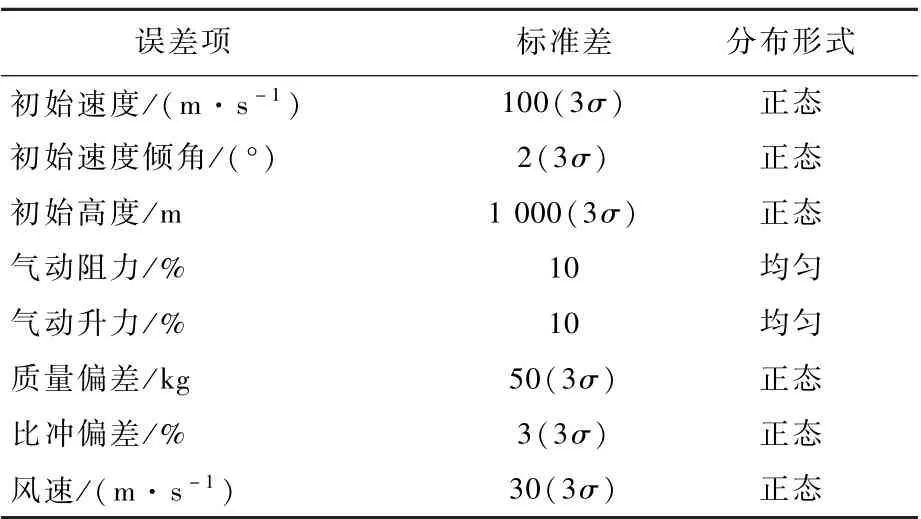
表4 蒙特卡罗仿真考虑的误差项Table4 Disturbances in Monte-Carlo simulation
采用本文方法对火箭动力减速段进行跟踪,500次蒙特卡罗仿真均成功求解,仿真结果如图13~图18所示。其中,图13~图15为速度误差、速度倾角误差和高度误差的变化过程,可见整个制导过程这些误差都快速减小,最终都收敛到较小值,说明轨迹跟踪中偏差修正的有效性。图16~图18为终端速度误差、速度倾角误差和高度误差的分布。可以看到,500次仿真中,3种终端误差分别位于[-1,0.6]m/s、[0.006,0.018]°、[15,18]m的区间内,处于可接受的范围。整体而言,当考虑初始干扰、风干扰和其他各种干扰因素下,采用本文方法轨迹跟踪性能良好,可以抵抗多种干扰因素可能导致的较大跟踪误差,全程跟踪精度良好,说明本文方法具有较强的抵抗模型不确定性和外界干扰的能力,具有良好的跟踪性能和鲁棒性能。
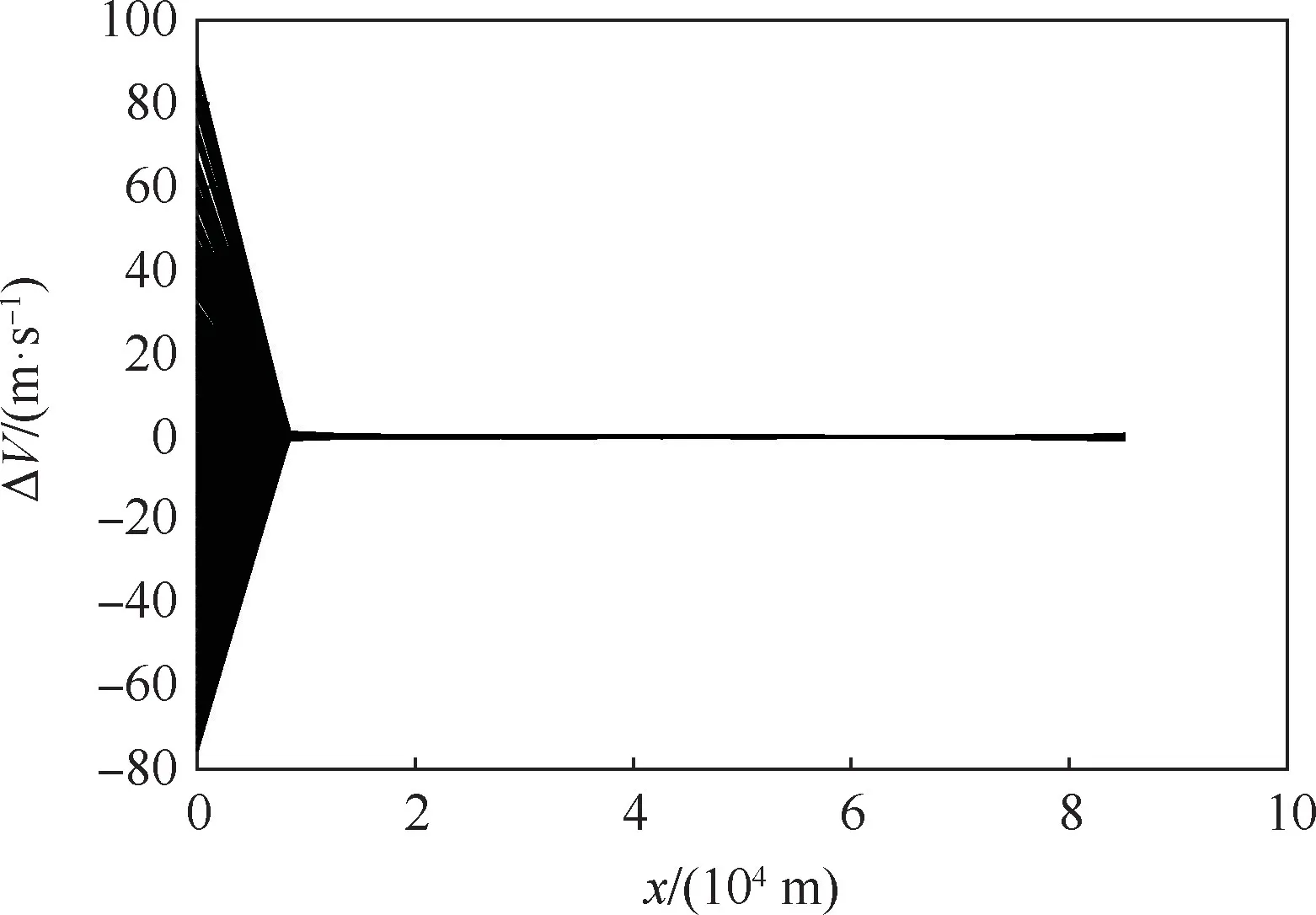
图13 速度误差(蒙特卡罗仿真)Fig.13 Velocity error(Monte-Carlo simulation)
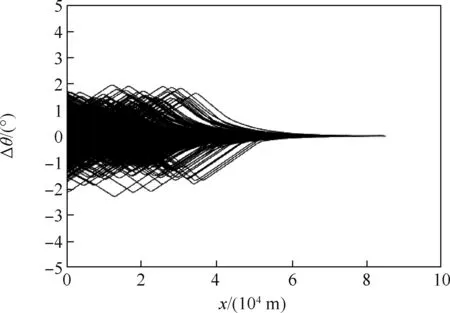
图14 速度倾角误差(蒙特卡罗仿真)Fig.14 Flight path angle error(Monte-Carlo simulation)
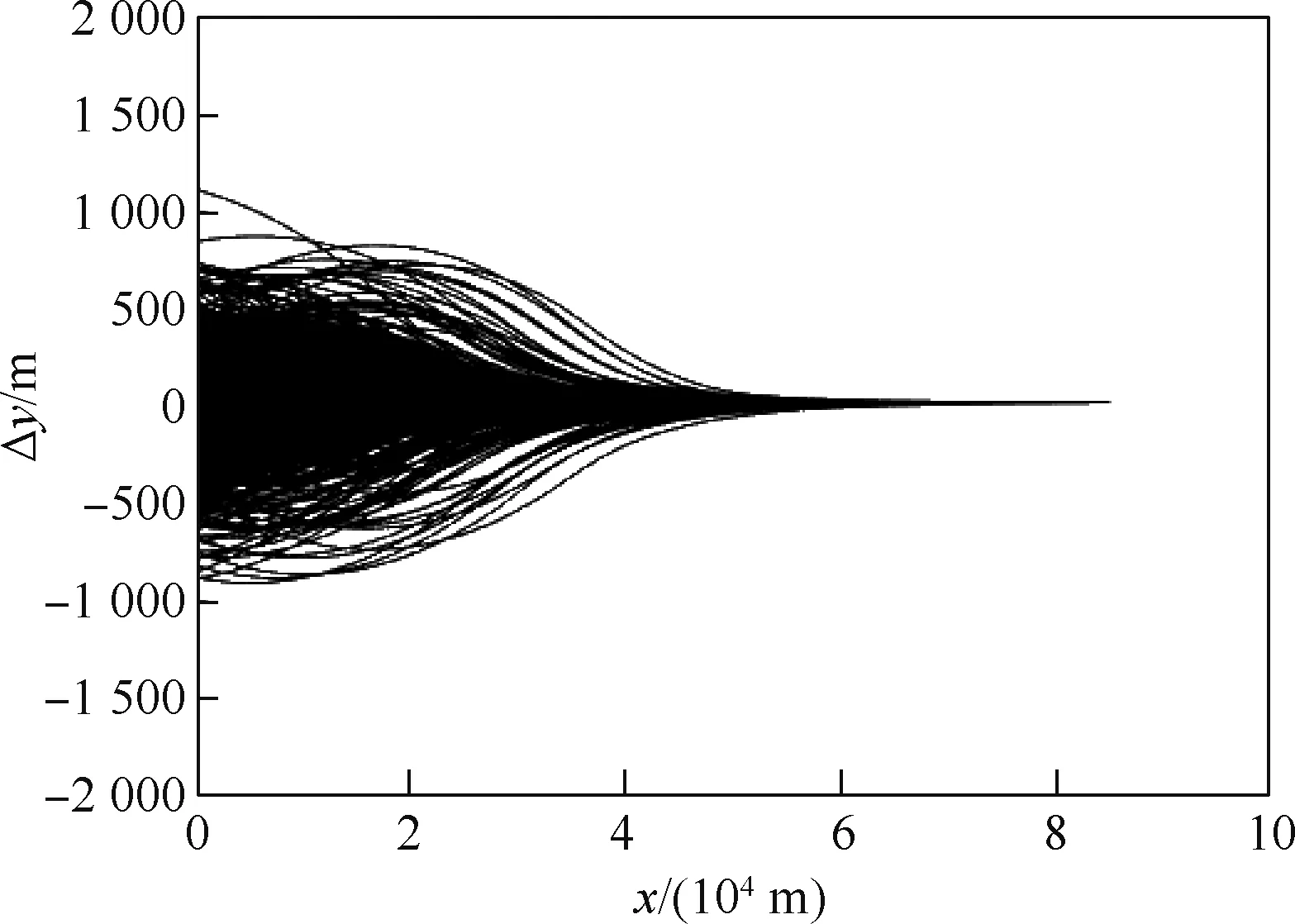
图15 高度误差(蒙特卡罗仿真)Fig.15 Altitude error(Monte-Carlo simulation)
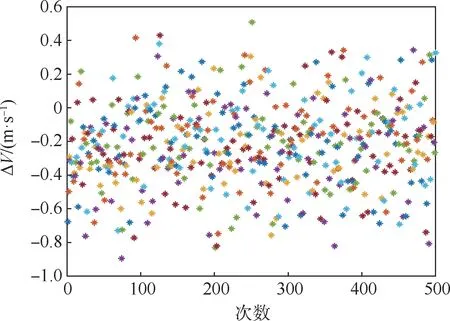
图16 终端速度误差(蒙特卡罗仿真)Fig.16 Terminal velocity error(Monte-Carlo simulation)

图17 终端速度倾角误差(蒙特卡罗仿真)Fig.17 Terminal flight path angle error(Monte-Carlo simulation)
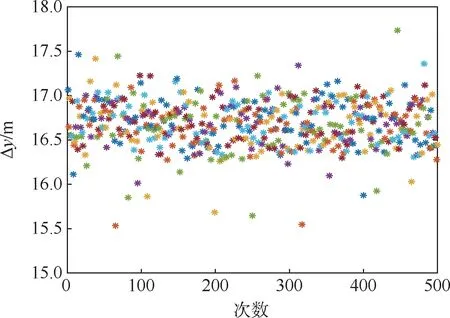
图18 终端高度误差(蒙特卡罗仿真)Fig.18 Terminal altitude error(Monte-Carlo simulation)
4 结 论
1)本文针对可重复使用运载火箭动力减速段,提出了一种基于LQR和分段凸优化的标称轨迹跟踪制导方法。将动力学模型分解为速度和位置相关的2部分,采用分段凸优化方法进行速度跟踪,同时最小化燃料消耗;采用LQR方法实现对火箭飞行轨迹的高精度跟踪,同时抵抗各种误差和干扰的影响。
2)采用数值仿真对本文方法进行验证,仿真结果表明,相对于传统的LQR跟踪制导方法,本文方法轨迹跟踪精度与LQR基本相当,对不确定性干扰具有较强的鲁棒性,但本文方法能一定程度降低燃料消耗,且无需基准轨迹对应的推力控制量信息,实际应用更加灵活。
3)本文方法采用分段控制策略,无需求解全段道优化控制问题,相较于直接滚动凸优化方法计算效率大幅提升,且具有较高的可靠性。本文方法也可应用于其他推力可控的飞行器轨迹跟踪制导,尤其是大气较为稠密的情况,其燃料节省效果将更加可观。
