微小卫星隐身构型设计及优化分析

秦远田,孙汗青,岳鑫

(1.南京航空航天大学 航天学院,南京 210093; 2.南京航空航天大学 电子信息工程学院,南京 210093)

微小卫星普遍具有研制周期短、发射难度小、成本低等特点[1],其与微纳卫星可以从质量上进行区分。微小卫星指质量在1000kg以下的人造卫星,包括小卫星、微卫星、纳卫星、皮卫星和飞卫星等,而微纳卫星的质量往往不足10kg,即微纳卫星包含于微小卫星。它们都为空间科学的蓬勃发展作出了巨大贡献[2]。

隐身卫星对未来空间攻防中起着至关重要的作用。针对卫星在不同探测系统下所面临的不同威胁,卫星隐身技术可以分为雷达隐身、红外隐身、可见光隐身和射频隐身[3]。其中,卫星的主要威胁之一来自雷达,设计和分析具有低雷达散射截面(radar cross section,RCS)外形设计的微小卫星就显得尤为重要。国内外关于隐身卫星研究进展的资料并不多见。1990年,美国朦胧计划的首星(Misty-1)成功发射,圆柱形的卫星本体下方有一锥形充气罩,地面发射的雷达波照射至锥形充气罩会折射至其他方向,使回波能量得到极大抑制[4],同时这也是世界上首颗在轨运行的隐身卫星。郑侃[5]依据多棱面设计思路,提出了3种隐身微小卫星构型,并通过RCS对比仿真,得到了多棱面锥体的隐身效果较优这一结论。朱冬骏等[6]提出了一种兼顾雷达隐身和光学隐身的卫星构型,其光学横截面积(optical cross section,OCS)峰值仅为0.082m2,不易被光学探测系统监视识别。

针对国内外学者对卫星隐身这一领域的研究还相对较少这一现状,本文通过对天巡一号进行电磁散射特性的数值模拟和分析,得到了RCS入射角、极化、频率、电尺寸等响应特性的分析报告,并对该卫星的构型进行优化使其能够实现RCS在某些角域乃至全向角域算术均值的进一步缩减,期望对今后微小卫星的隐身设计提供技术参考。

1 RCS数值计算流程

1.1 隐身微小卫星电磁计算模型

天巡一号星体为拥有交错斜置外形设计的多面体,从底部到顶部依次为1个正六边形底面(用于安置对接环,实现星箭分离)、6个矩形面、6个倾斜梯形面和6个倾斜三角形面,如图1所示。其中,矩形面和梯形面均安装有太阳能贴片,可随时为卫星提供能源支持。当星体尖顶向下时可实现对地雷达隐身,尖顶向上时可实现对天雷达隐身。

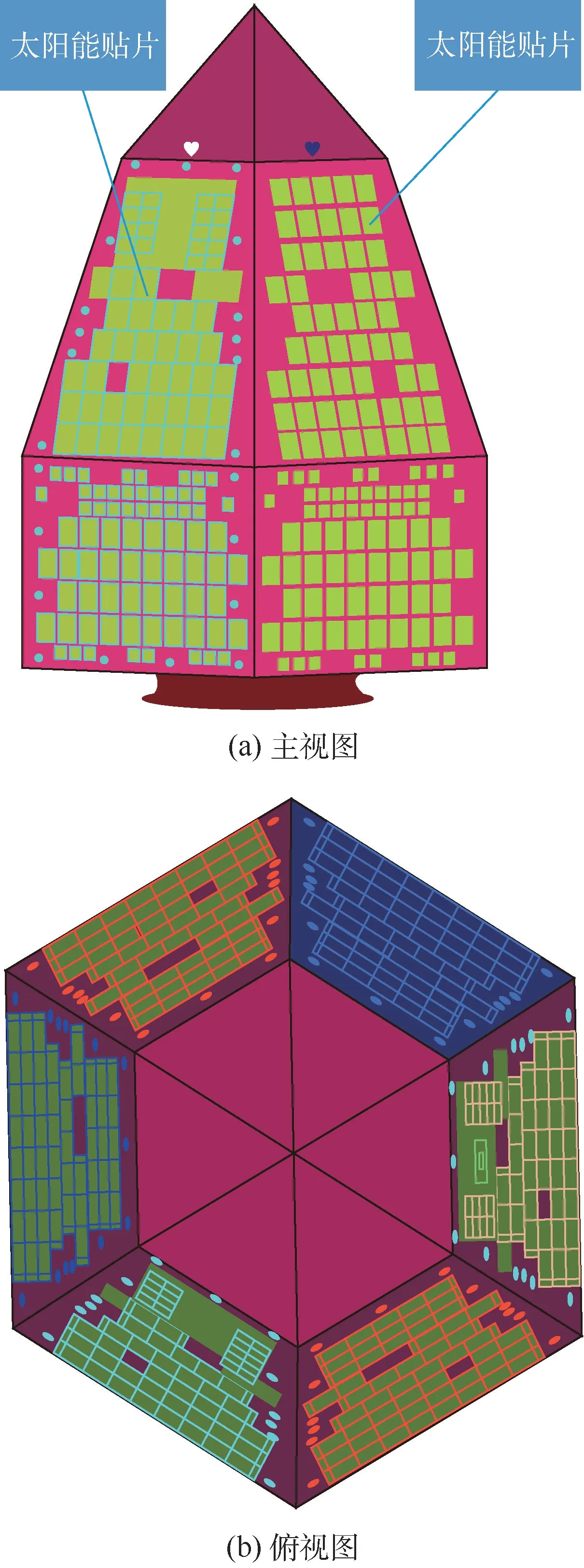
图1 天巡一号的电磁计算模型Fig.1 Electromagnetic calculation model of TX-1

1.2 RCS数值计算方法

从计算电磁学的角度出发,RCS计算方法可分为微分方程法、积分方程法、有限元法及适用于目标在光学区的高频近似方法。在本文所研究的频率范围内,卫星目标主要处于光学区。矩量法(method of moment,MOM)就是典型的积分方法,通过对矩阵采用直接计算,不存在收敛性的问题,而且由于采用面网格进行划分,未知量的总数大大降低,但是因为“源”之间存在耦合,所以矩阵属于稠密矩阵,从而导致MOM计算速度慢[7-11],大多数用于一些精细电小或电中尺寸的RCS计算。多层快速多极子(multi level fast multipole method,MLFMM)在MOM的基础上采用了加速算法,既降低了内存需求又提高了计算速度,可用于电大尺寸的RCS求解,但迭代求解时遇到病态矩阵容易出现不收敛的情况,如飞机进气道、尾喷之类的腔体结构。物理光学法(physical optics,PO)主要适用于目标在光学区的散射特性求解,从斯特拉顿-朱兰成(Stratton-Chu)散射场积分方程出发,通过切平面近似方法假设目标表面电流值等于积分面元处目标为理想光滑平面时的电流值,并据此来对物理光学电流进行积分得到目标远区散射场[12-16]。根据切平面近似所得到面元RCS的平方根为

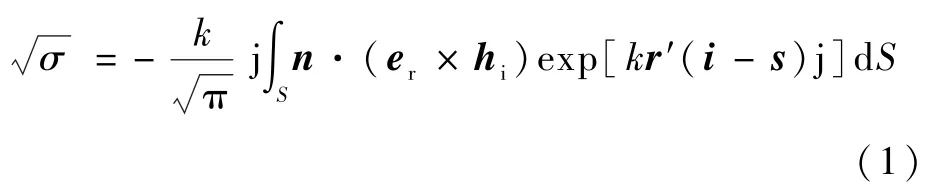
式中:n为积分面元处的法向矢量;k为入射电磁波数量;S为小面元的面积;er和hi分别为接收天线的电场单位矢量和发射天线的磁场单位矢量;i和s分别为电磁波入射方向的单位矢量和散射方向的单位矢量;r′为“源”的位置矢量。

由于式(1)是基于PO的单个面元RCS平方根的表达式,有着有限个网格的目标按相位叠加得到的总RCS[16]为

式中:σi为第i个网格面元的RCS。

1.3 目标隐身性能分析方法

为使卫星具备较好的雷达隐身能力,卫星全姿态下的RCS需处于一个较低的范围内,这是因为雷达探测距离与目标RCS密切相关。雷达作用距离方程式为

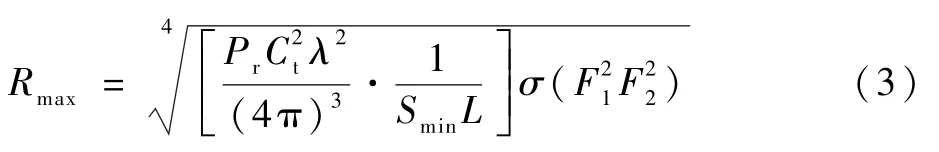
式中:Pr为接收信号的功率;Ct为发射/接收天线功率增益;λ为波长;Smin为最小可探测信号;L为发射机的内部损耗;σ为目标雷达散射截面;为从发射天线到目标的方向图传播因子;为从目标到接收天线的方向图传播因子。

由式(3)可以看出,雷达性能和大气传播系数无法人为改变,要想降低雷达作用距离,最好的方法就是降低目标RCS。由Rmax∝σ1/4可知,当RCS每缩减10dBsm,就可以使雷达作用距离降低44%;当RCS缩减40dBsm时,雷达探测距离可降低90%。因此,可通过缩减目标RCS来降低雷达探测距离,从而使目标躲避雷达探测。

除此之外,还可以选用RCS算术均值和RCS幅值来更加具体直观地分析目标的隐身性能。

式中:σm为RCS幅值;σi为第i个入射角下的RCS值;¯σ[a,b]为[a,b]角域内的RCS算术均值。

1.4 卫星散射特性计算流程

图2给出了本文建立的卫星模型RCS求解流程,主要由前处理模块、求解计算模块及后处理模块3部分组成。

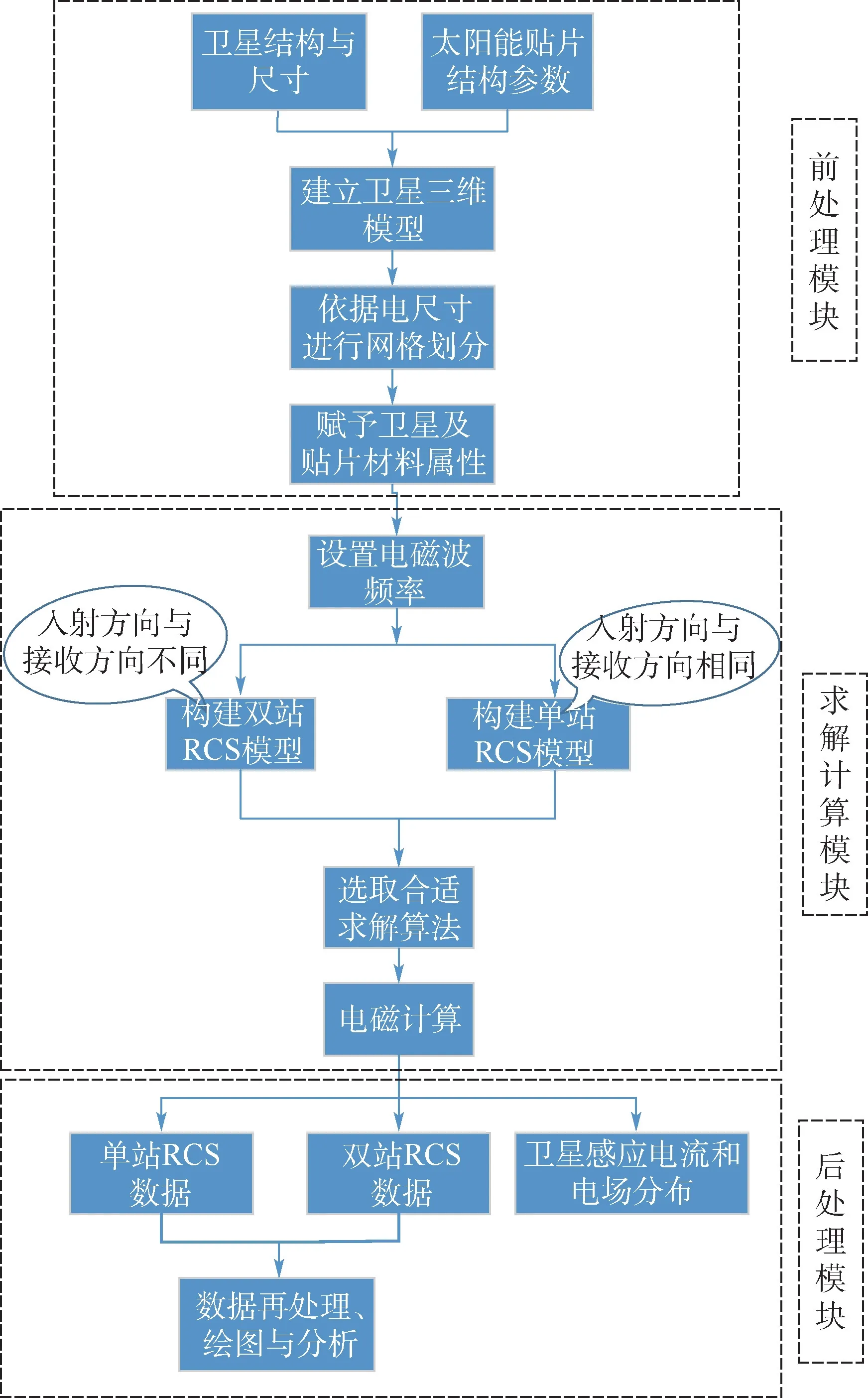
图2 卫星电磁散射计算流程Fig.2 Calculation process of satellite electromagnetic scattering

2 样星微波暗室试验验证

在C波段(5.45GHz)电磁波激励下的天巡一号处于光学区,具有高频散射特性,分别使用PO和微波暗室测试来求解天巡一号的后向雷达散射截面(单站RCS)。由于PO为近似方法,在计算结果上可能会存在较大误差,需要验证PO数值模拟出的RCS的准确性。图3给出在上述条件下PO与微波暗室测试所得到的RCS对比结果。

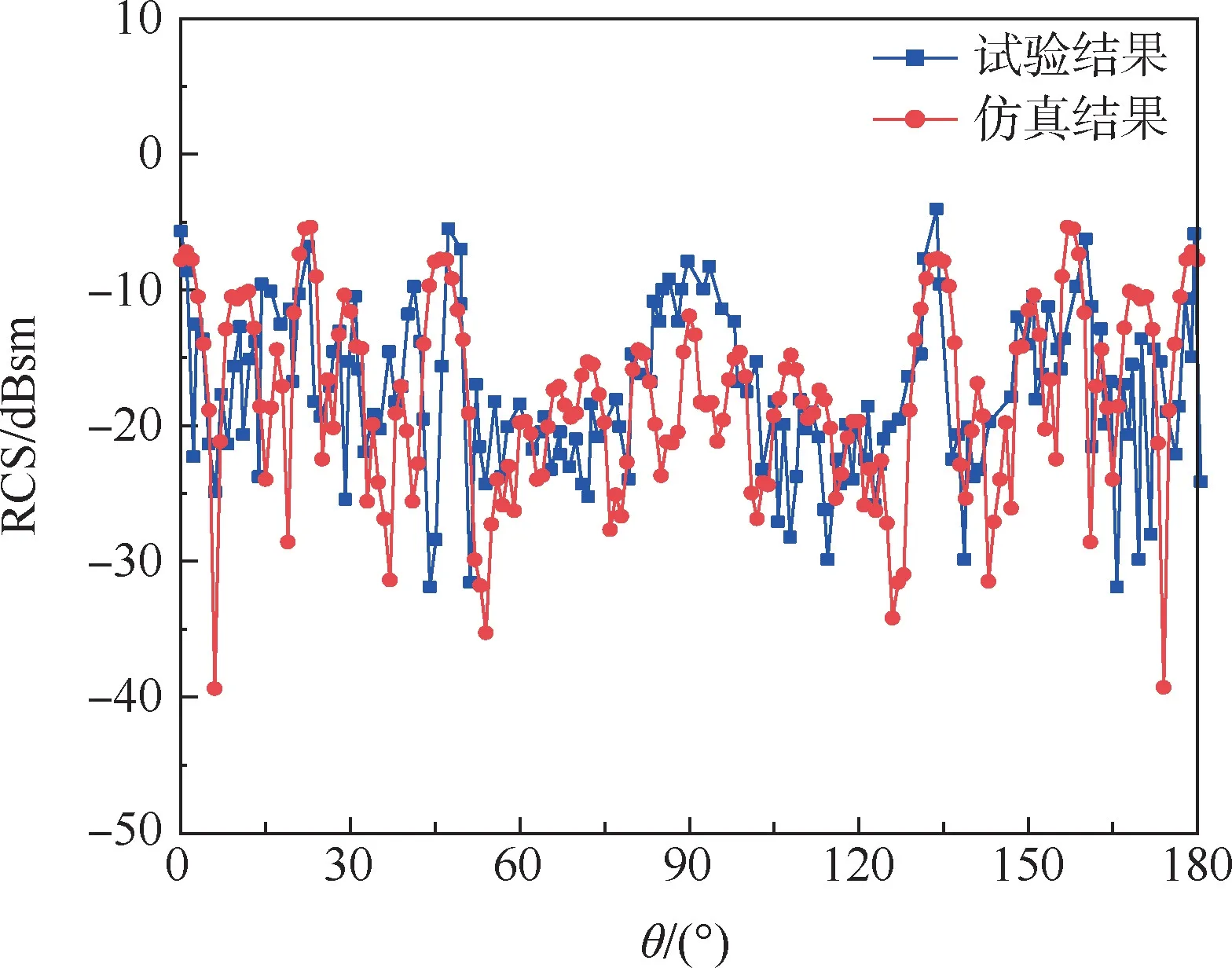
图3 数值仿真与试验结果对比Fig.3 Comparison of numerical simulation and experimental results

由图3不难看出,采用PO求解出的RCS值与在微波暗室试验所得到的卫星RCS实测值吻合度较高。具体来看,在90°为中心的(即正对卫星尖顶处)84°～96°这一对称角域内,试验结果有一明显波峰,正好对应了天巡一号尖端处。此角域内试验结果明显高于仿真结果,这是因为PO是采用切平面近似的方法,简单地假定被积目标表面是完全光滑平坦的,直接将表面场代入积分方程,所以PO并不能很好地求解尖顶散射问题。除去此误差较大的角域后,仿真和试验所得到的RCS均值分别为-17.86dBsm和-17.96dBsm,两者仅相差0.1dBsm,证明了在光学区时采用高频近似方法来求解卫星RCS的准确性和可行性。

少数角域内数据还存在误差,主要是测试时卫星是用铝箔贴敷表面,难免存在缝隙、贴合不平整等问题。此外,卫星模型在测试时的姿态摆放也会存在误差,这些都是导致测试结果与仿真结果不能完全相符的主要原因。

3 天巡一号电磁散射特性分析

卫星隐身状态下,双站RCS计算模型的入射角为0°、30°、60°,而非隐身状态下的双站RCS计算模型的入射角为120°、150°、180°。单站计算模型较双站则简化许多,本文采用周向360°入射,周向360°接收(发射天线和接收天线处于同一位置)。具体雷达波入射示意如图4所示。图中:Ψ为散射角。

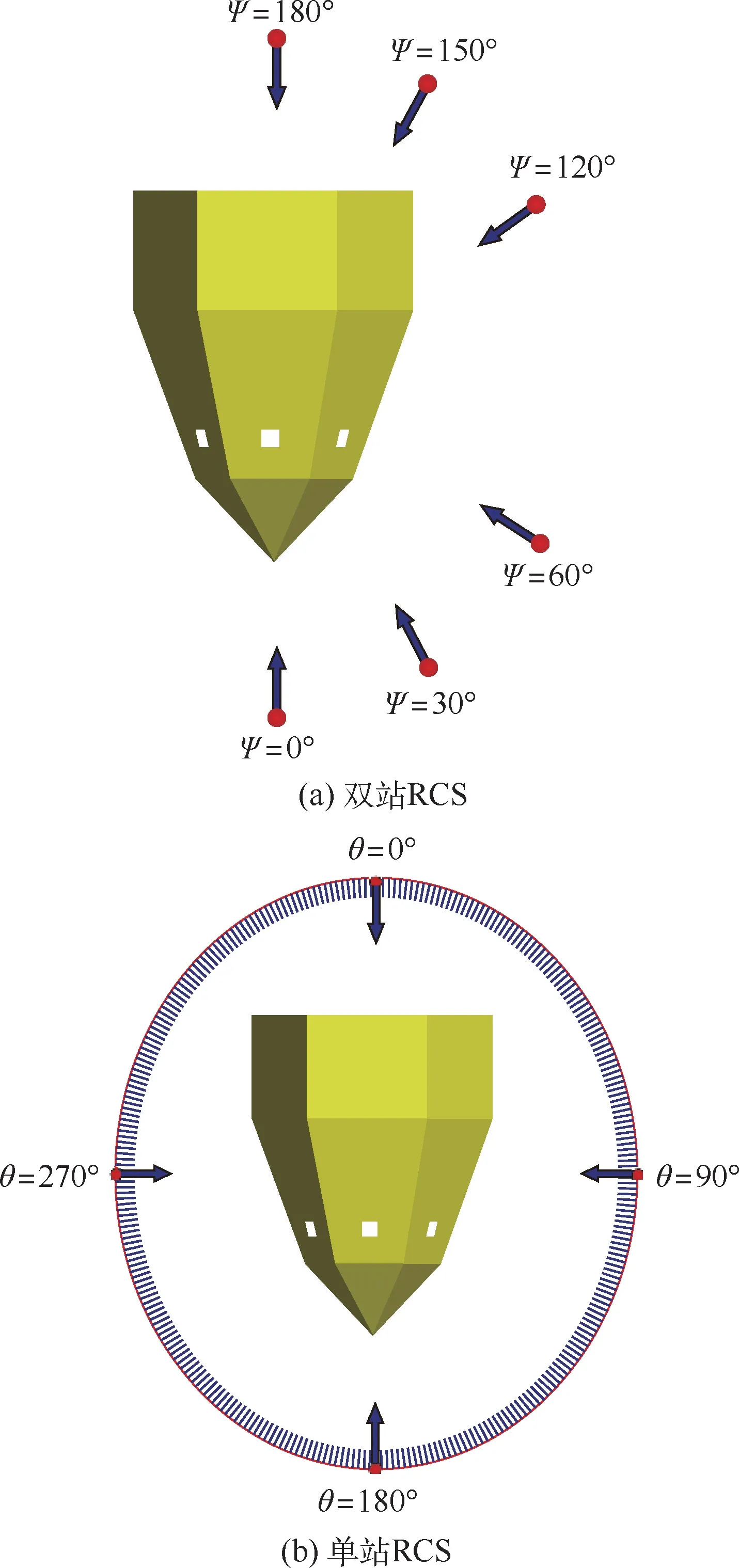
图4 双站和单站RCS入射示意图Fig.4 Schematic of bistatic and monostatic RCS incidence

3.1 RCS入射角响应特性

图5给出了电磁波从地面和太空方向入射,步长均为30°时天巡一号的双站RCS入射角响应曲线分布。图中:Φ为入射角,0°≤Φ≤60°代表卫星隐身姿态下电磁波入射,120°≤Φ≤180°代表卫星非隐身姿态下电磁波入射。

由图5和表1不难看出:

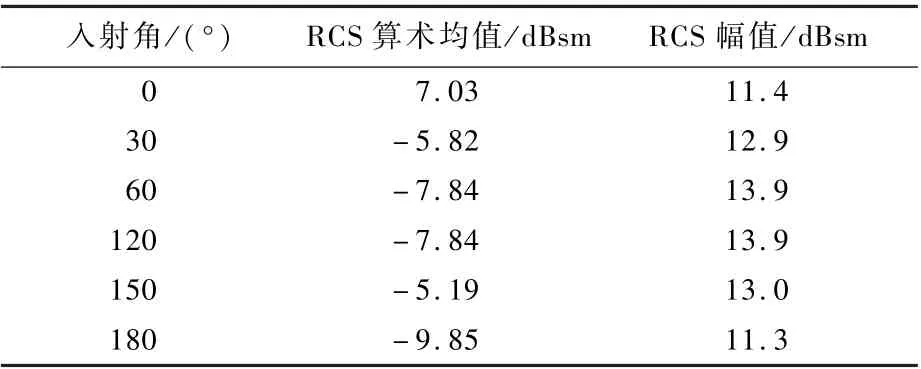
表1 不同入射角下双站RCS算术均值和幅值Table1 Average value and amplitude of RCS at bistatic with different incidence angles

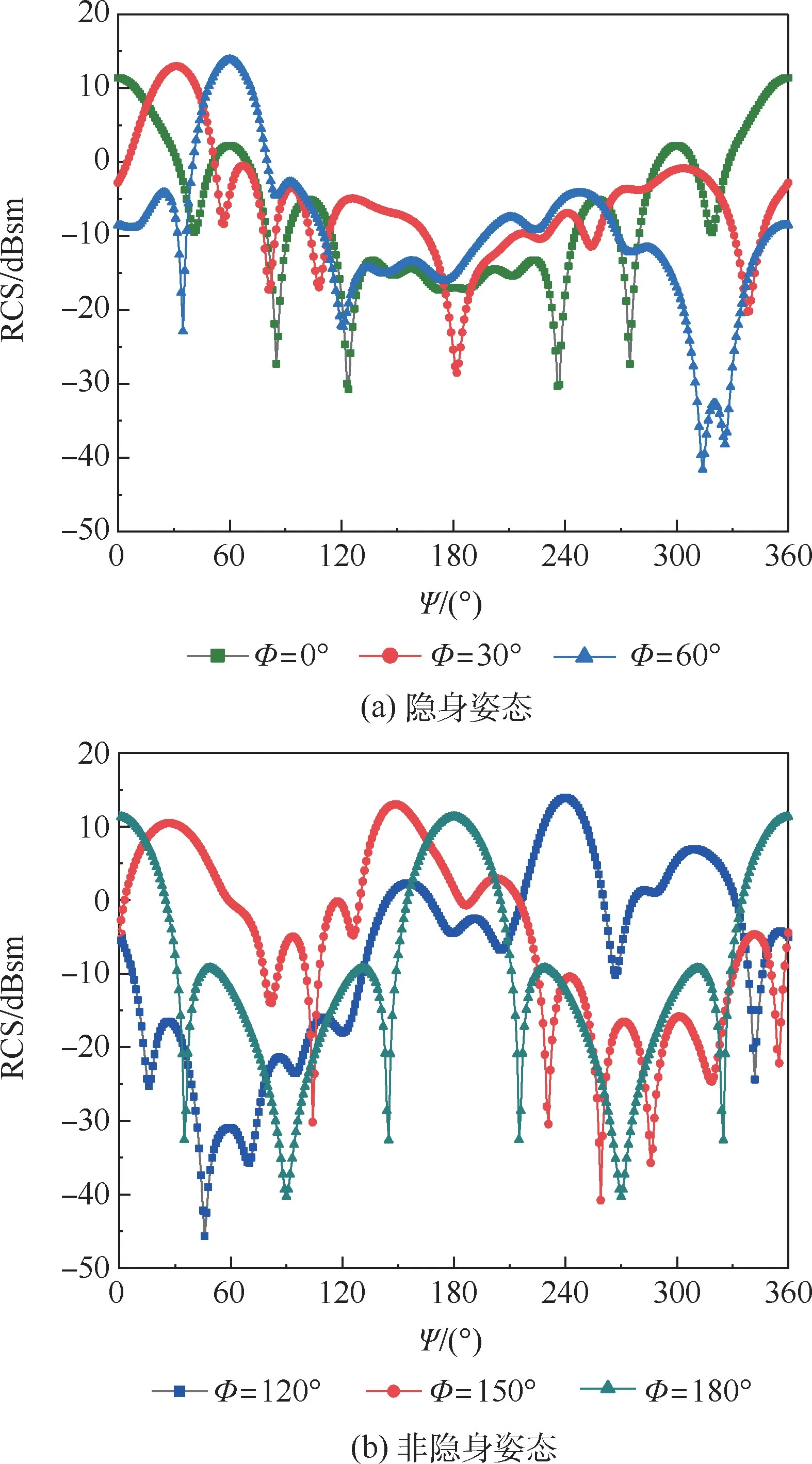
图5 不同入射角下双站RCS分布特性Fig.5 Characteristics of RCS distribution at bistatic with different incidence angles

1)当0°≤Φ≤60°时,双站RCS分布曲线的幅值出现在0°、30°、60°处,即散射角Ψ=Φ时;当120°≤Φ≤180°时,双站RCS分布曲线的幅值出现在240°、150°、180°处,即散射角Ψ=Φ或Ψ=360°-Φ。

2)在0°≤Φ≤60°和120°≤Φ≤180°散射角域内,RCS幅值和均值相差不大,0°均值约等于120°处均值,30°均值约等于150°处均值,60°均值约等于180°处均值。由此可知,天巡一号的隐身姿态对比非隐身姿态的双站RCS并无明显缩减,即隐身姿态不能有效应对来自双站雷达的探测和威胁。

3.2 RCS极化响应特性

为探究极化形式对天巡一号RCS的影响,图6给出了天巡一号在4种不同极化形式下的RCS极化响应特性曲线。

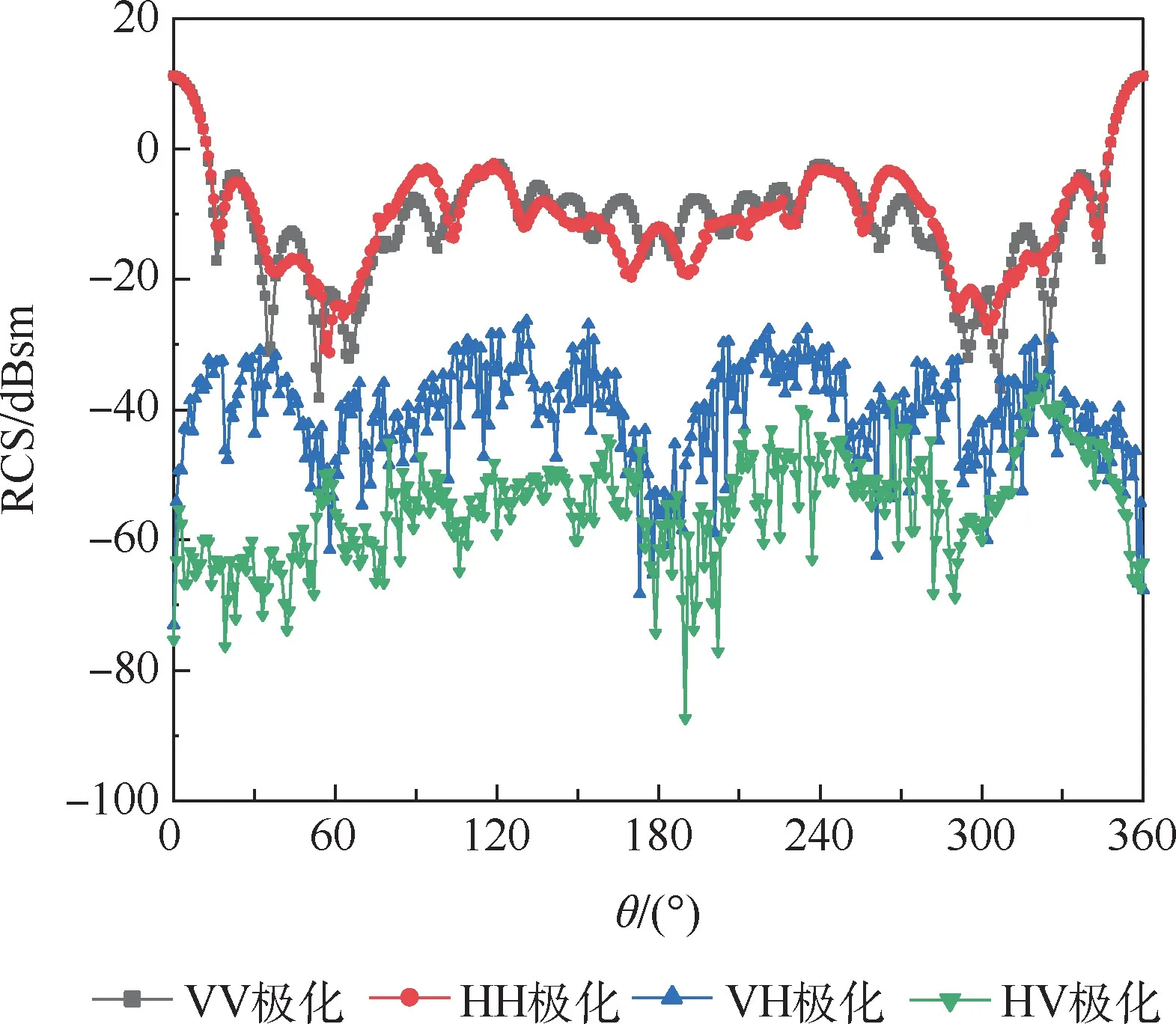
图6 天巡一号RCS极化响应特性Fig.6 RCS polarization response characteristics of TX-1

由图6可以看出,同极化的单站RCS值要高于交叉极化30～40dBsm,且曲线分布更为平缓。2种同极化(HH、VV)的单站RCS吻合度也较高,但交叉极化(VH、HV)之间RCS值差异明显。此外,同极化下的单站RCS在0°(360°)处有一主瓣,但交叉极化却无明显主瓣。由以上分析可得,天巡一号的RCS与入射场和接收天线的极化形式有关,同极化下的RCS要显著高于交叉极化。

3.3 RCS频率响应特性

图7和图8分别给出了天巡一号随频率变化下的单站RCS响应分布和RCS算术均值统计。选用的电磁波频率f为1～16GHz(涵盖了L、S、C、X和Ku波段),步长为3GHz,可以看出:

图7 天巡一号RCS频率响应特性Fig.7 RCS frequency response characteristics of TX-1

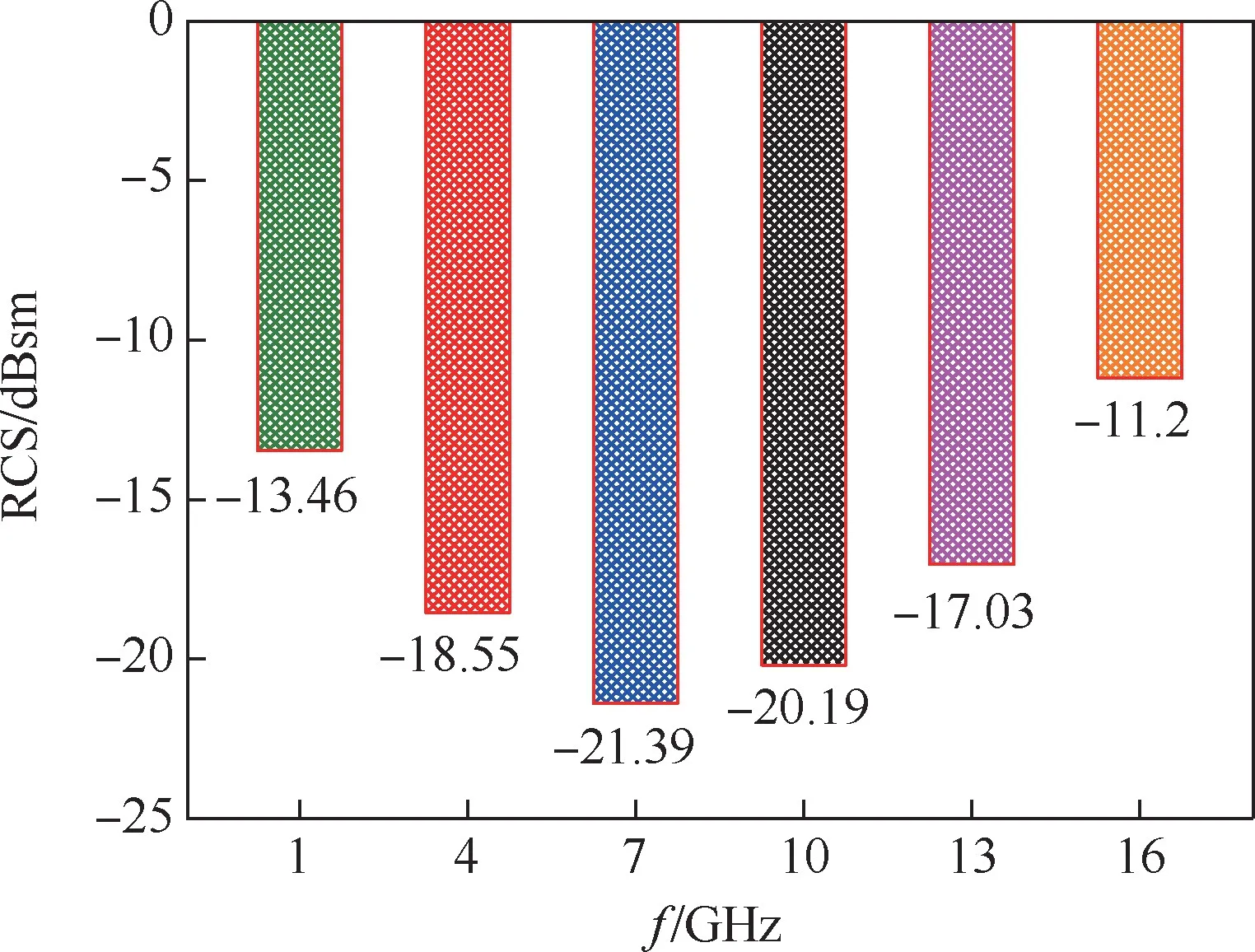
图8 不同频率下RCS算术均值对比Fig.8 Comparison of RCS average values at different frequencies

1)当电磁波频率从L波段增大至C波段时,RCS算术均值逐渐降低;当电磁波频率从C波段增大至Ku波段时,RCS均值逐渐升高。即RCS算术均值随频率增大会出现先减小再增大这一特点。

2)天巡一号在全波段(指L～Ku波段)下RCS峰值为35.4dBsm(16GHz下散射角为0°时),最小值低至-45.57dBsm(1GHz下散射角为306°时),RCS算术均值在-11.2～21.39dBsm,具有较低的电磁散射特征和较好的雷达隐身性能。

3)随着入射雷达波频率的升高,在入射角为0°(360°)和180°处的RCS极大值呈现逐渐升高的趋势,但散射的波束宽度变小,响应曲面也更加尖锐,表明目标散射特性更加集中。RCS频率特性分布曲面主要有2处极值,分别分布在0°附近角域和180°附近角域,正好对应卫星正六边形底面的镜面反射和头部尖端处的尖顶散射。

3.4 RCS电尺寸响应特性

为探究模型电尺寸l(实际尺寸比上工作波长)改变对目标RCS的影响,图9给出了电尺寸l从3～30变化时天巡一号RCS电尺寸响应分布曲线。可以看出:

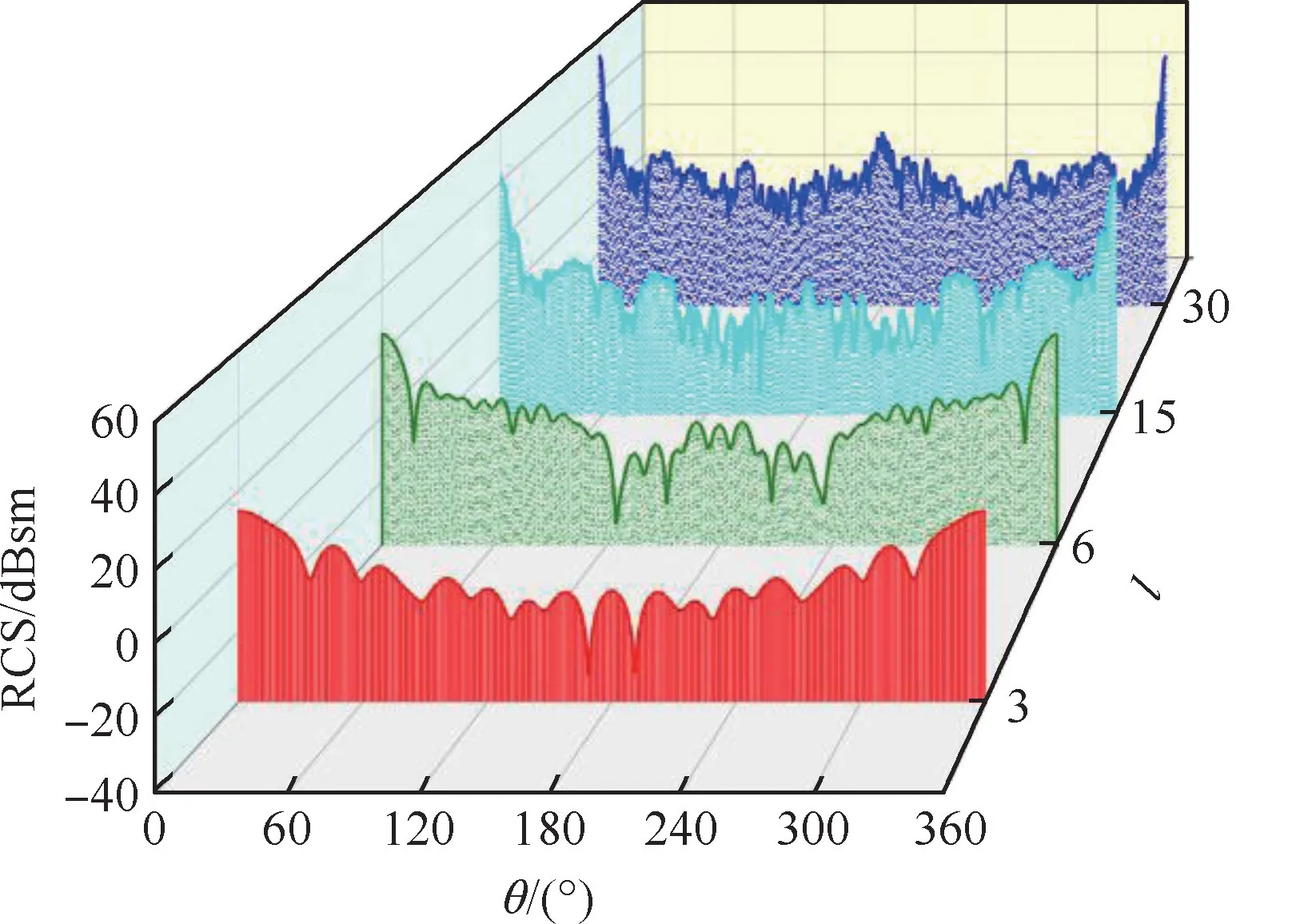
图9 天巡一号RCS电尺寸响应特性Fig.9 RCS electric size response characteristics of TX-1

1)无论电尺寸如何变化,RCS曲线的总体分布特性无明显改变,RCS幅值均出现在0°(360°)处。电尺寸较小时,RCS曲线波动平缓;电尺寸较大时,RCS曲线波动则明显加剧。

2)直观来看,随着电尺寸不断增加,曲线振荡程度加剧,天巡一号RCS幅值、算术均值均有上升。具体来看,当目标处于谐振区,即电尺寸由3增大至6时,RCS曲线整体略有升高但增速缓慢,波峰数量下降且散射的波束宽度也开始变小,呈现字母“W”形状;当目标处于光学区,即电尺寸由15增大至30时,RCS分布曲线整体呈明显上升趋势且增速变快,但各波峰位置无明显改变。

3.5 全姿态角下空间RCS响应特性

为进一步研究和分析天巡一号的隐身能力和强弱散射源分布情况,采用多角度雷达波组成的3种全姿态入射球面来照射天巡一号,3种入射姿态分别为隐身姿态、最佳隐身姿态和非隐身姿态,入射步长均为1°。

图10和图11分别给出了3个不同姿态角下天巡一号的空间RCS分布云图、RCS算术均值和幅值对比,分析可以发现:

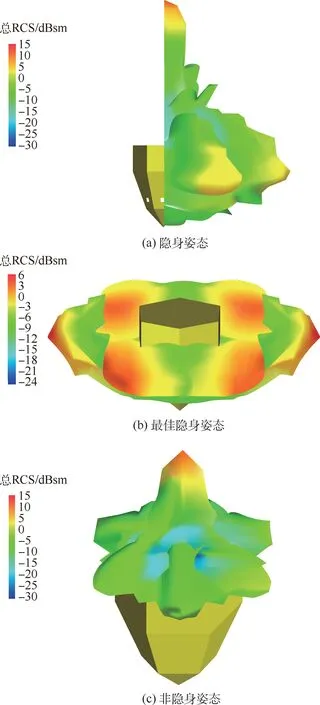
图10 天巡一号全姿态角空间RCS响应云图Fig.10 TX-1full attitude angle RCS response cloud

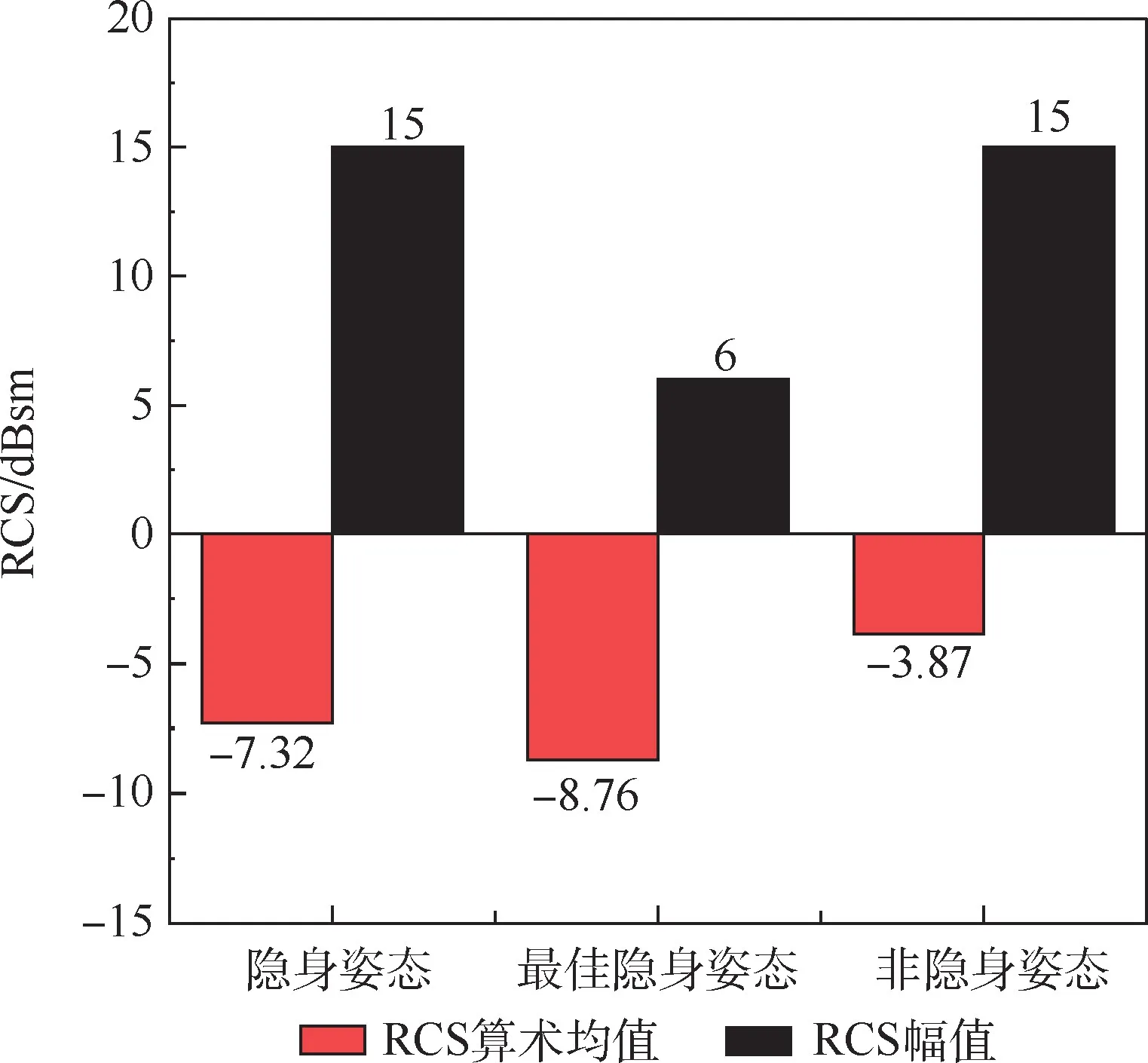
图11 天巡一号全姿态角空间RCS对比Fig.11 TX-1full attitude angle RCS comparison

1)由于设计卫星构型时并未打算实现全姿态隐身,而是使卫星拥有隐身姿态和非隐身姿态,如图10所示,下半球面即为最佳隐身姿态,右边球面为隐身姿态,上半球面为非隐身姿态。由RCS云图对比可知,隐身与非隐身姿态下单站RCS差异显著。

2)天巡一号的正六边形底面及与底面有公共边的6个矩形面是卫星的强散射源,而采用斜置外形的三角形面和梯形面为弱散射源。这主要是为了方便在底面安装对接环实现星箭分离,但光滑的正六边形底面会带来强烈的镜面反射,使卫星RCS升高,其他角域下天巡一号的RCS均处在一个比较理想的范围内。

3)以下半球面这一最佳隐身姿态作为参考,与隐身姿态下RCS最大值相差9dBsm,但RCS算术均值仅相差1.44dBsm,即隐身姿态的隐身性能与最佳隐身姿态相差不大;与非隐身姿态下RCS最大值相差9dBsm,RCS算术均值相差4.89dBsm,即非隐身姿态的隐身性能要明显低于卫星最佳隐身姿态。

4 天巡一号隐身构型优化

4.1 卫星构型优化设计方法

通过第3节对天巡一号隐身特性和散射源强弱的分析可知,天巡一号具有较好的隐身性能,但可通过进一步优化其隐身构型来实现更低的RCS和更宽的隐身角域。

图12为优化隐身微小卫星天巡一号构型的具体思路和方法。首先,参考天巡一号隐身构型,得到呈对称结构的四棱边尖锥构型;然后,继续增加对称尖锥的边数,至八棱边(即优化构型A)和十棱边(即优化构型B),如图13所示;最后,利用极限的思想将棱边数取到足够大,即得到最终的优化构型(橄榄体)。

图13 两种卫星优化构型Fig.13 Two satellite optimized configurations

4.2 构型优化方法验证

为验证图12中优化方法的可行性,分别选取S波段和X波段的中心频点来分析天巡一号、优化构型A、优化构型B和橄榄体的隐身性能。下面先给出S波段(3GHz)下4种隐身构型的RCS数值计算结果对比。

由图14和表2不难发现,在S波段下,最终隐身构型橄榄体在算术均值和幅值上相比较于天巡一号分别缩减了4.77dBsm和31.66dBsm。从RCS算术均值出发,判断4种构型的隐身性能为:橄榄体＞构型B＞构型A＞天巡一号,这也印证了图12中的构型优化方法。下面给出4种隐身构型在X波段下RCS分布情况。

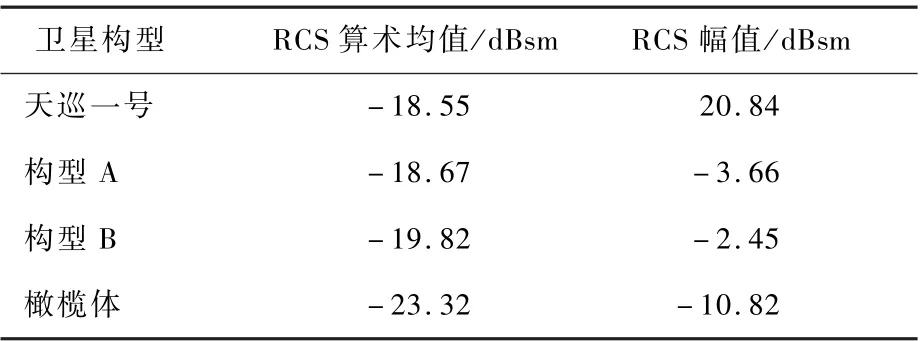
表2 四种卫星构型3GHz下RCS算术均值和幅值对比Table2 Comparison of average and amplitude values of RCS for4kinds of satellite configuration at3GHz

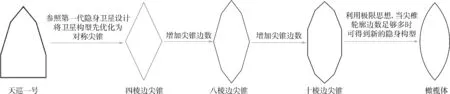
图12 一种卫星构型优化方法Fig.12 A satellite configuration optimization method

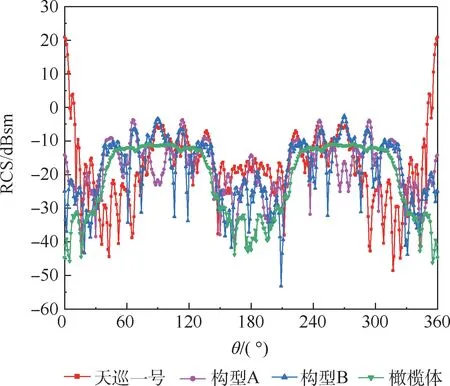
图14 四种卫星构型3GHz下RCS分布Fig.14 RCS distribution of4kinds of satellite configurations at3GHz

由图15和表3不难发现,在X波段下,规律更加明显,即无论是从RCS算术均值还是RCS幅值来看,4种构型的隐身性能均为:橄榄体＞构型B＞构型A＞天巡一号。橄榄体构型RCS算术均值和幅值分别低于天巡一号3.65dBsm和43.97dBsm,构型A和构型B也有不同程度上的RCS缩减,并且构型B的缩减效果优于构型A。由此也再次验证了图12中优化设计方法的正确性和可行性。此外,橄榄体构型在以90°和270°为中心的对称角域内RCS分布十分平缓,反观另外3种构型的RCS曲线则振荡剧烈,存在较多散射波峰,这对于隐身构型设计来说是极为不利的。

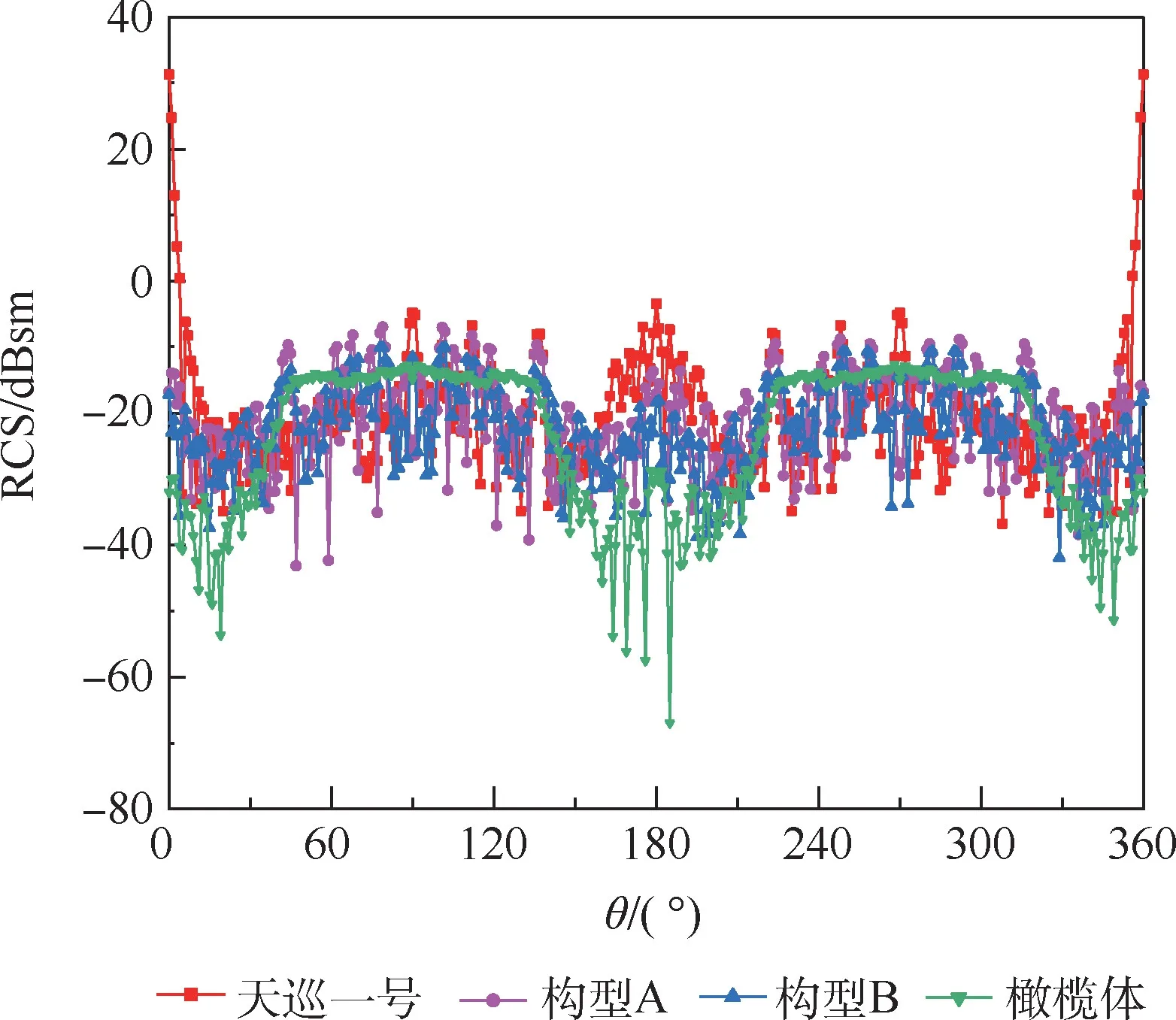
图15 四种卫星构型10GHz下RCS分布Fig.15 RCS distribution of4kinds of satellite configurations at10GHz

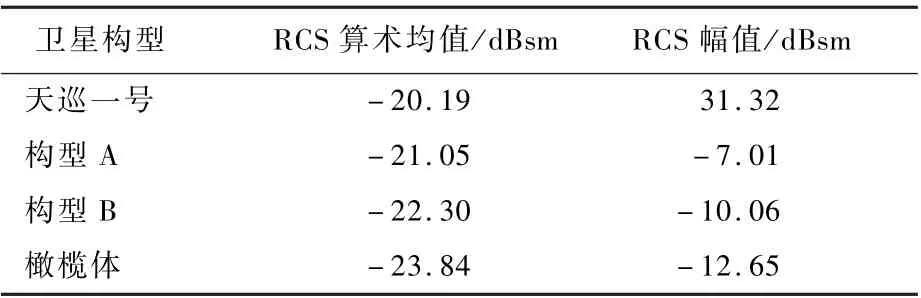
表3 四种卫星构型10GHz下RCS算术均值和幅值对比Table3 Comparison of average and amplitude values of RCS for4kinds of satellite configuration at10GHz

5 结 论

为了探究天巡一号及其优化构型的电磁散射特性,本文分析了多种响应下的RCS分布曲线。同时,将PO计算出的天巡一号RCS和微波暗室实测值对比,证明了采用PO求解是准确且合适的。在参考天巡一号隐身构型设计的基础上,构建一对称尖锥作为初始模型,在验证优化方法的可行性后,利用极限思想得到了最终的橄榄体隐身构型,并通过RCS对比仿真论证了橄榄体在隐身性能上的提升。

1)对于双站雷达,天巡一号隐身姿态和非隐身姿态下的RCS算术均值与RCS幅值均相差不大,表明天巡一号的隐身姿态并不能有效应对双站雷达探测与威胁。

2)对于单站雷达,由于正六边形底面无任何隐身设计,具有较强的镜面反射,导致其后向雷达散射截面较高。但就其隐身姿态而言,天巡一号交错斜置的多棱面外形发挥了极佳的隐身效果,可将雷达波反射至入射波所在方向以外的其他方向,从而大幅降低了单站RCS。2种隐身姿态下单站RCS算术均值分别为-8.76dBsm和-7.32dBsm,相比较非隐身姿态RCS均值分别下降了4.89dBsm和3.45dBsm。证明了天巡一号的隐身姿态在应对单站雷达探测时可发挥更好的隐身性能。

3)对称尖锥是一种在雷达隐身上优于单侧多棱面锥体的构型设计,是本文在优化得到橄榄体卫星过程中的“桥梁”。在10GHz下,4种隐身构型的RCS算术均值和幅值均符合“橄榄体＜构型B＜构型A＜天巡一号”这一特点,表明从增加尖锥棱边数这一角度来优化隐身构型是可行的。

4)寻求低电磁散射特性的构型是卫星隐身设计中至关重要的一环。在参考原设计(天巡一号)的基础上,通过不断优化对称锥体得到了橄榄体隐身卫星。橄榄体构型无论是在S波段还是X波段,隐身性能均有了显著提升,RCS幅值缩减超过30dBsm,RCS算术均值缩减也超过3dBsm。除此之外,与另外3种构型相比可知,橄榄体构型RCS曲线平缓度较好,散射波峰数量也有明显下降,这也会在一定程度上降低卫星被雷达探测系统监视识别的可能性。

本文工作为今后设计和优化微小卫星隐身构型提供了一种新的思路和参考。