飞机旋转表面结冰数值模拟
2022-11-30郭琦申晓斌林贵平张世娟
郭琦,申晓斌,2,*,林贵平,张世娟
(1.北京航空航天大学 航空科学与工程学院,北京 100191;2.中国空气动力研究与发展中心 结冰与防除冰重点实验室,绵阳 621000; 3.武汉航空仪表有限责任公司,武汉 430074)
飞机在结冰气象条件下飞行时,其迎风面上会积聚过冷水滴,发生冰的聚积,该现象为飞机结冰[1]。飞机积冰对飞机性能有重要影响,会造成升力和失速迎角减小,阻力增加[2],甚至导致严重的飞行事故[3]。随着航空科学技术的快速发展,航空飞行器得到广泛运用,由于飞机结冰引发的飞行安全问题愈发凸显。目前对飞机结冰的研究有结冰气象条件的探测、过冷水滴的撞击特性、结冰热力学模型与冰形预测、结冰对飞行性能的影响等,本文针对飞机旋转表面结冰进行数值模拟研究。
目前主要通过实验研究与数值仿真分析,对飞机结冰展开研究,其中数值方法具有经济性好、执行周期短等优点,并且由于计算流体力学技术和计算机技术的不断发展与成熟,数值仿真在飞机结冰研究中的作用越发重要。在国内外学者的共同努力下,飞机结冰数值模拟已取得了相当大的进展,结冰数值研究的内容由霜冰预测发展到了明冰的模拟,由二维计算逐步向三维仿真推进,由固定部件表面向旋转部件表面发展,三维旋转表面复杂流动结冰机理与模拟成为了目前研究的焦点。
传统的结冰计算一般采用Messinger[4]结冰热力学模型,该模型假设某个控制体中的未凝结液态水会全部流出到其他控制体中,没有考虑到控制体自身存在水膜的情况。美国国家航空航天局(NASA)于20世纪80年代研发成功的LEWICE软件[5]就是基于该结冰模型开发的。之后在Messinger模型的基础上,发展出了Myers[6]模型和Shallow-Water[7]结冰热力学模型,两者都考虑了控制体表面水膜存在的情况,不同的是,Myers模型还考虑了冰层和水膜中的温度梯度分布。加拿大的FENSAP-ICE软件[7],是利用Shallow-Water模型对结冰表面的冰形进行求解。基于这些结冰模型,国内外学者对飞机结冰展开了一系列模拟仿真研究。易贤等[8]发展了一种采用迭代求解的三维结冰热力学模型,该模型基于传统的Messinger二维模型,引入了结冰表面溢流水的流动。申晓斌等[9]基于Messinger结冰模型,建立了一种适用于三维结冰表面的液态水溢流模型,并完成了对三维发动机结冰冰形的计算。曹广州等[10]采用Myers结冰模型,对三维机翼模型的结冰增长和表面液态水流动进行了仿真求解,且能够在计算中自动辨别过冷水滴在结冰表面发生碰撞后的结冰冰形。Cao和Huang[11]在Myers模型的基础上,建立了三维结冰模拟模型,计算了后掠机翼的冰形。雷梦龙等[12]基于Myers结冰热力学模型,对其结冰类型判别方法进行改进,采用离散算法对表面液态水溢流和冰层生长过程进行计算,模拟了机翼表面的结冰过程。
同时,随着飞机结冰模拟技术的发展,各国学者针对飞机旋转部件结冰仿真计算也进行了多项研究。Bain等[13]用LEWICE3D软件进行旋转桨叶的结冰计算,将旋转结冰过程分为2个步长进行计算,没有考虑旋转作用对表面水膜的作用力及对流动特性的影响。Reid等[14-15]基于Shallow-Water溢流模型,利用旋转坐标系的方法对旋转桨叶的结冰进行了模拟。Switchenko等[16]针对旋转桨叶采用二维截面的方法简化计算,通过二维多步法模拟特征截面处的结冰情况。Wang与Zhu[17]在旋转坐标系下计算了流场与水滴撞击特性,考虑离心力对溢流水膜分配的影响,进行了结冰分析。Dong等[18]采用欧拉法求解了发动机处的水滴撞击特性,根据结冰热力学平衡模型得到了旋转帽罩的结冰冰形。赵秋月等[19]基于拉格朗日法,对旋转部件表面的水收集系数计算方法进行研究,将其用于发动机旋转整流帽罩的水滴撞击特性计算,发现整流罩表面的局部水收集系数会随着转速和锥体锥角的增大,沿表面外形线下降加快,撞击区域减小。吴孟龙等[20]基于欧拉法对发动机旋转帽罩三维表面的水滴撞击特性进行模拟,研究帽罩表面的水滴撞击特性受旋转速度的影响,发现旋转速度对帽罩表面的水滴撞击特性影响较小。
现在使用的结冰热力学模型几乎都是在固定部件表面建立的,一般认为空气剪切力为水膜的驱动力,用其来确定水膜的流动特性,而对于旋转部件表面的受力分析及旋转作用对水膜运动的影响分析较少,很少考虑离心力和科里奥利力的方向与大小对结冰效果的作用,旋转结冰过程中的运动力学与传热学机理研究尚不全面。本文采用Shallow-Water结冰模型,对飞机旋转表面的水膜流动和结冰冰形进行模拟,并分析转速、水滴直径和液态水含量等因素对旋转表面结冰的影响,为飞机旋转部件的结冰研究提供参考。
1 数学模型
为了研究旋转表面的水膜流动和结冰冰形,基于Shallow-Water结冰热力学模型[7],分析结冰表面水膜的流动与传热过程,建立动量守恒方程、质量守恒方程和能量守恒方程,进而计算旋转坐标系下的非稳态结冰过程与冰形。
1.1 动量守恒方程
旋转表面的水膜主要受到空气剪切力、压力梯度、重力、旋转导致的惯性力等因素的影响,选取表面微元控制体进行受力分析,如图1所示。用S表示曲面的表面,S′表示S在法向量n方向的投影,则S和S′之间的距离就是水膜的厚度h。
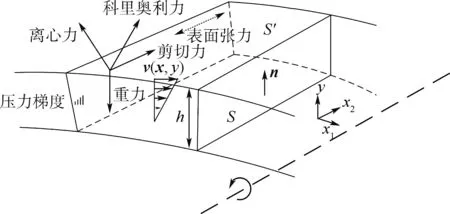
图1 旋转表面水膜受力分析示意图Fig.1 Schematic diagram of force analysis of water film on rotating surface
由于水膜在结冰表面流动速度较小,且不考虑水滴撞击的影响,对水膜作常物性处理,可假设结冰表面的水膜流动为不可压层流流动[10],基于不可压流体的雷诺平均Navier-Stokes方程对水膜溢流过程进行建模,在旋转坐标系下其动量方程表述为
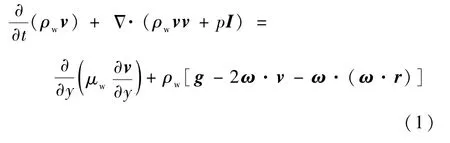
式中:ρw为水的密度;v为水膜相对速度;p为水膜内部压力;I为单位张量;μw为水的动力黏度;y为表面法向坐标;g为重力加速度;ω为转速;r为当地矢径。其中,方程右边第2项为惯性力项,包括了科里奥利惯性力与牵连惯性力。
考虑结冰表面的水膜厚度很小,其主要受空气剪切力和旋转导致的惯性力的作用,忽略非稳态项、压力梯度项和重力项的影响[21],则动量方程可简化为
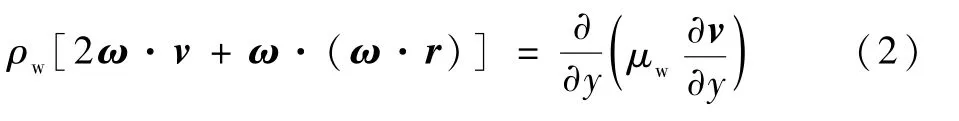
水膜沿表面的流动方向为x=(x1,x2)。垂直方向水膜流动的边界分别是水膜-固体表面界面和空气-水膜界面。
水膜-表面界面在旋转参考系下的条件为

空气-水膜界面处,由于表面水膜很薄,水膜的速度梯度由空气剪切力占主导作用,边界条件为

式中:τ为水膜所受的空气剪切力。
根据动量方程(2)和边界条件(3)、(4),得到旋转坐标系下,水膜速度沿y方向的分布:
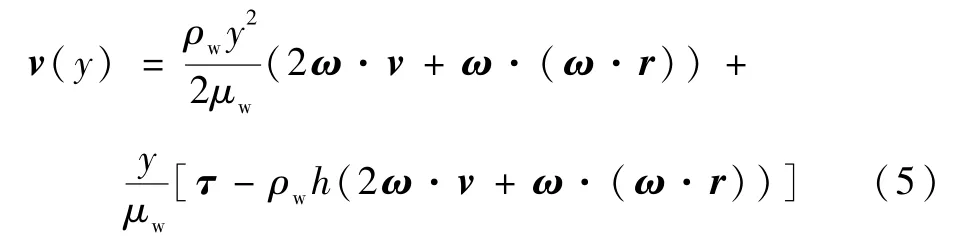
水膜和壁面交界处,速度为0;水膜顶端,速度达到最大值。在法向进行积分平均化,得到水膜的相对速度为
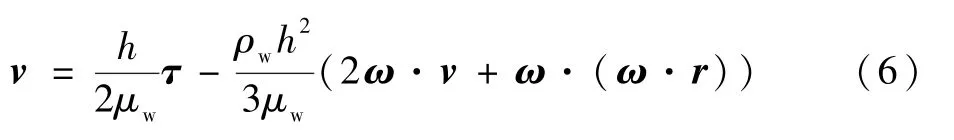
可见,水膜速度是由惯性力加速度和剪切应力共同决定的,而惯性力加速度与该速度本身有关,存在耦合关系,在求解过程中需要通过耦合迭代求解的方式予以处理。
1.2 质量守恒方程
图2为所有流入与流出控制体的质量,包括:控制体上表面水滴的撞击和蒸发或升华,下表面冰的生成,同时还有水的流入流出,以及控制体自身水膜厚度的变化[10]。
根据图2可得质量守恒方程为
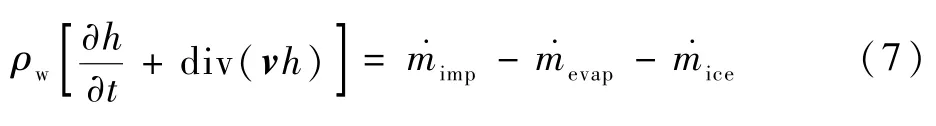
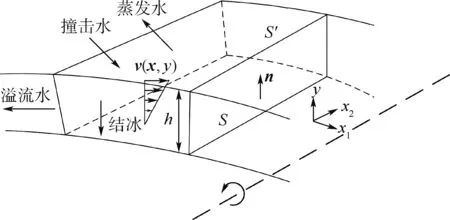
图2 控制体质量守恒示意图Fig.2 Schematic diagram of mass conservation of control volume
式(7)可表示为

式中:v1和v2分别为水膜平均速度v在x1和x2方向分量的大小。
由于非稳态计算中,是对每一个时间步长进行分别计算,需要将结冰时间分成多个时间步长,每一个时间步长作为一个稳态。因此,对质量守恒方程进行离散求解,可表示为
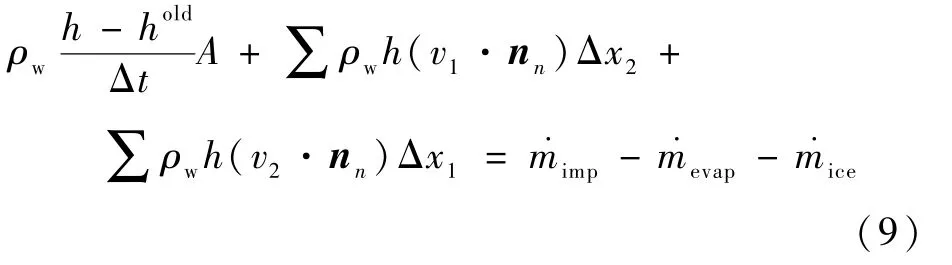
式中:hold为上一时间步长控制体内的水膜厚度;A为控制体底面面积;Δt为时间步长;nn为流入流出面的单位外法向量;Δx1和Δx2分别为当前控制体的底面边长。
式(9)中,等号左边第1项对应的是控制体内水膜质量随时间的变化,第2和第3项表示控制体内液态水在x1和x2方向所有的流入流出。从而,可将每个时间步长结冰计算中的质量守恒方程表示为
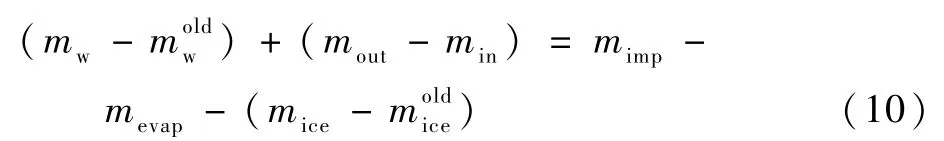
式中:m和m分别为上一时间步长控制体内存在的水膜和冰层的质量;mw和mice分别为当前时间步长控制体内存在的水膜和冰层的质量;min和mout分别为当前时间步长流入和流出该控制体的液态水质量;mimp为当前时间步长撞击到控制体表面的液态水质量;mevap为当前时间步长控制体内液态水蒸发的质量。
当前时间步长控制体内液态水膜质量为

假设水滴均匀撞击在控制体表面,当前时间步长撞击到控制体表面的液态水质量为

式中:v∞为远场来流速度;LWC为液态水含量;β为局部水收集系数。
当前时间步长流出该控制体的液态水质量为

式中:ln为流出面的底边长度。
计算当前时间步长控制体内蒸发水的质量,其中,蒸发速率可通过Chilton-Colburn比拟理论确定,利用对流换热系数hc确定相应位置的对流传质系数kc,如下:
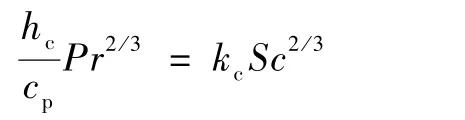
式中:Sc为Schimidt数;hc为对流换热系数;kc为对流传质系数;cp为定压比热;Pr为普朗特数,从而可推导蒸发速率为
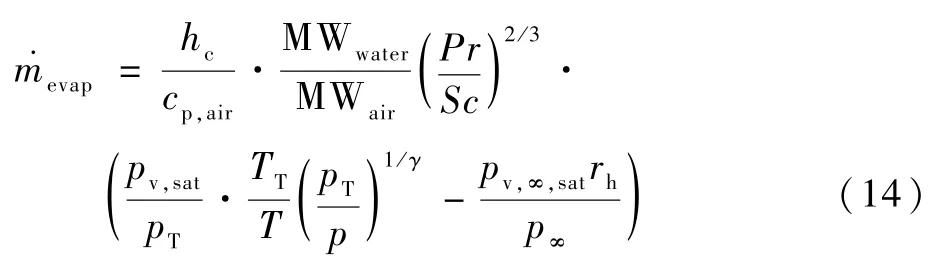
式中:cp,air为空气的定压比热;MWwater和MWair分别为水和空气的分子量;pv,sat为饱和蒸气压;pT和TT分别为总压和总温;T为当前时间步长控制体温度;p为壁面控制体绝对压力;rh为相对湿度;在水膜表面该值为1;pv,∞,sat为入口饱和蒸气压;p∞为入口环境压力。
同时可定义冻结系数f,是指在微元表面上实际结冰量和控制体内所有水之比:
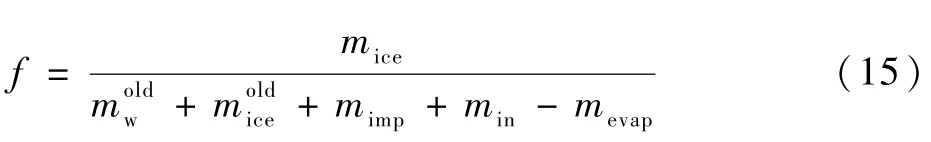
1.3 能量守恒方程
图3为控制体内的能量守恒示意图,设流入能量为正。其中,流入控制体的能量包括水滴撞击带来的能量,从邻近控制体流入的水带来的能量和控制体内结冰释放的能量,流出控制体的能量包括对流换热、导热、热辐射带走的能量,蒸发或升华带走的能量和流出控制体的水带走的能量[7]。由于导热和热辐射对能量传递的影响较小,一般可忽略。
根据图3可得能量守恒方程为
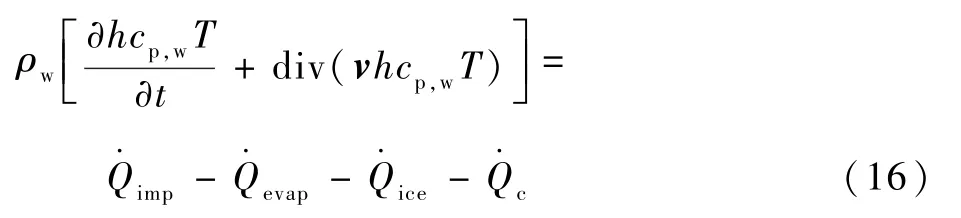
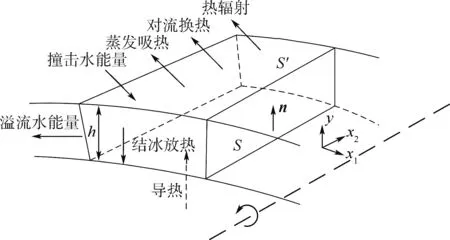
图3 控制体能量守恒示意图Fig.3 Schematic diagram of energy conservation of control volume
式中:cp,w为水的定压比热容;T为当前时间步长控制体的温度;imp为单位时间撞击水携带的能量;evap为单位时间蒸发水带走的能量;ice为单位时间所结冰层携带的能量;c为单位时间对流换热带走的能量。
式(16)可表示为
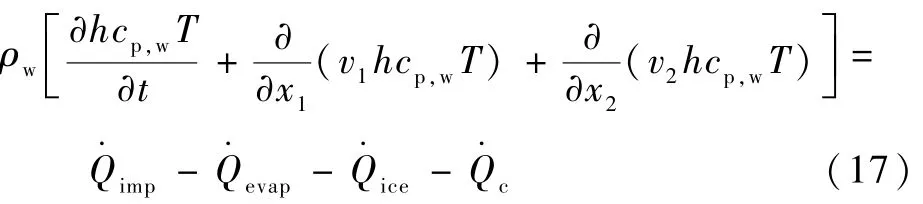
参考质量守恒方程,对式(17)进行离散求解,可得
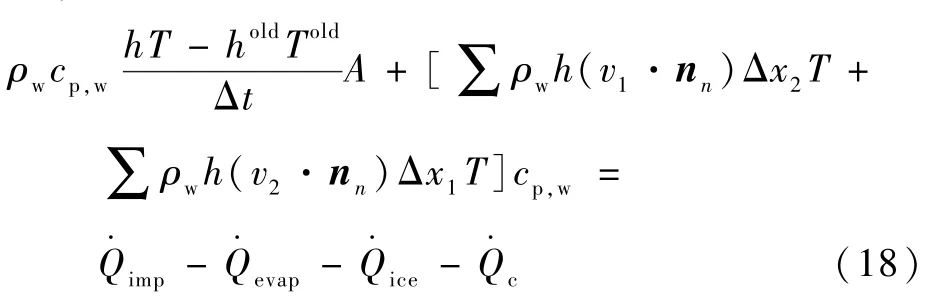
式中:Told为上一时间步长控制体的温度;等号左边第1项对应的是控制体内水膜自身携带的能量随时间的变化;第2项表示在x1和x2方向控制体内所有的流入流出的液态水携带的能量。从而,可将每个时间步长结冰计算中的能量守恒方程表示为

式中:Q和Q分别为上一时间步长计算结束后控制体内存在的水膜和冰层自身携带的能量;Qw和Qice分别为当前时间步长控制体内存在的水膜和冰层自身携带的能量;Qimp为撞击水携带的能量;Qin和Qout分别为流入和流出该控制体的水携带的能量;Qevap为水膜蒸发带走能量;Qc为对流换热带走的能量。
上一时间步长计算结束后控制体内存在的水膜和冰层自身携带的能量为
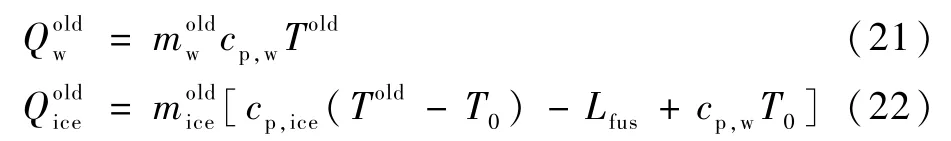
式中:cp,ice为冰的定压比热容;Lfus为结冰时的固化潜热;T0=273.15K。
当前时间步长控制体内存在的水膜和冰层自身携带的能量为
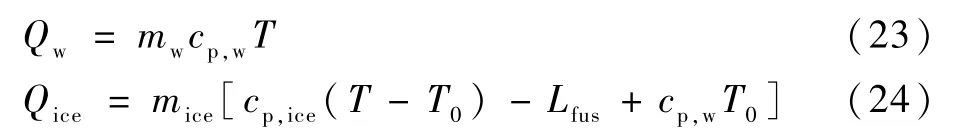
撞击水携带的能量为

式中:T∞为远场来流温度。
流出该控制体的水携带的能量为

水膜蒸发带走的能量Qevap,在不同结冰情况下采用不同的计算公式。
若没有发生结冰,即控制体内是液态水膜时:
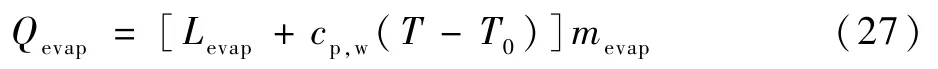
若发生部分结冰,即结明冰情况下,控制体内温度处于相变平衡温度时:

若全部结冰,即结霜冰情况下:
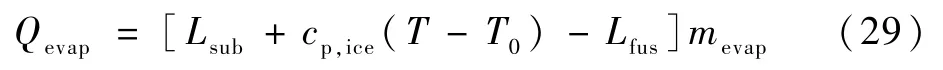
式中:Levap和Lsub为凝固点温度时的蒸发潜热和升华潜热。
对流换热带走的能量:

令Q=Qin+Qimp-Qevap-Qout-Qc,联立式(20)~式(30),对能量守恒方程进行求解,可得到结冰冰层质量为
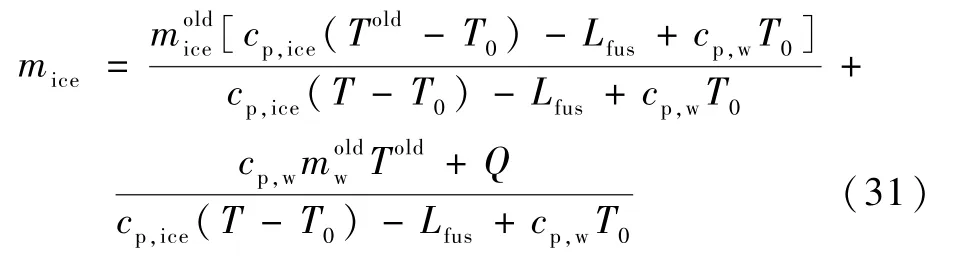
2 求解方法
通过动量方程、质量和能量守恒方程及引入的冻结系数,联立方程式(6)、式(10)、式(15)、式(31)可以对结冰数学模型进行求解。
基于Fluent计算得到的外部空气-水滴流场数据[22],利用Fluent提供的用户自定义函数(user defined function,UDF),求解旋转结冰数学模型,发展了一种循环遍历控制体的非稳态迭代求解方法。具体步骤如下:
步骤1在上一时间步水膜与冰厚的基础上(初始时刻都为0),对动量方程式(6)迭代求解,得到所有微元控制体内水膜的平均速度和相应的流动方向。
步骤2根据水膜的流动速度和方向,循环全部控制体,找到边界及驻点位置作为计算的开端。
步骤3从驻点处开始对控制体展开计算,假设控制体内初始温度为0℃,并全部结冰,计算控制体内的质量和能量守恒方程,从而得到冻结系数f,对冻结系数进行判断,得到其结冰类型(明冰、霜冰、不结冰),根据结冰类型更新冻结系数、温度、结冰量、溢流水量、水膜厚度等。利用更新的结果迭代计算动量方程、质量和能量守恒方程,直至收敛,该控制体计算完成,将当前控制体溢流水流出量作为输入值,赋值给临近控制体,邻近控制体流入的溢流水质量可知。
步骤4继续计算邻近控制体,直至全部控制体计算完成,并利用更新后的水膜厚度,对全部控制体内水膜速度进行更新,返回步骤1开始计算,直至完成收敛判断,则当前时间步长计算完成,输出当前时间步长冰形。
步骤5进入下一时间步长结冰计算,直至所设定结冰时间全部计算完成。
上述步骤的具体流程如图4所示。

图4 旋转表面结冰求解流程Fig.4 Flow chart for solving icing on rotating surfaces
其中步骤3和4为结冰计算关键,对其进行进一步详细说明:
1)假设控制体初始结冰状态。假设初始控制体温度为0℃,控制体内结明冰,且水全部发生冻结,可知mout=0,mw=0,Qout=0,Qw=0,且m和m对应上一时间步长的液态水量和结冰量,为已知量。
通过上述假设可以对式(31)求解,得到结冰量,从而可根据式(15)得到冻结系数f。
2)对冻结系数f进行判断。
①当f≥1时,说明此时控制体结霜冰,控制体内水全部发生冻结,没有溢流水流出,控制体内不存在液态水,令f=1,则可得
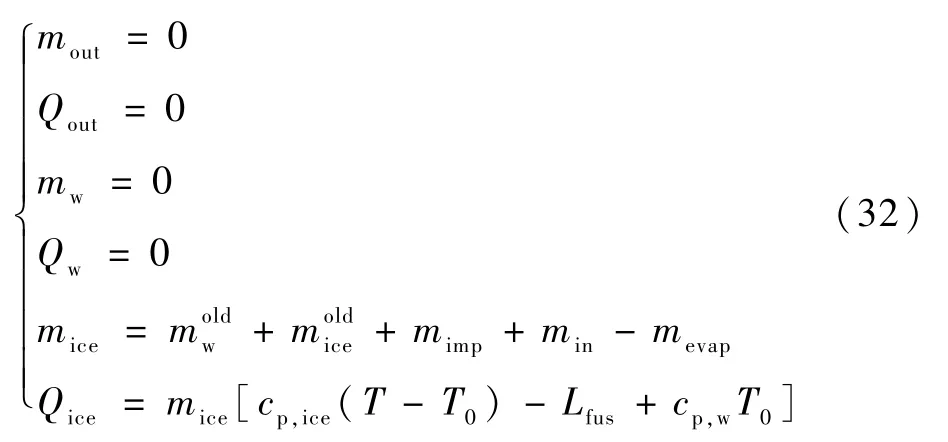
②当0<f<1时,说明此时控制体结明冰,部分水发生冻结,控制体温度处于相变平衡温度。控制体内结冰量由式(31)可知,且联立式(10)、式(11)、式(13)可得

联立式(33)和式(34)可得水膜厚度为
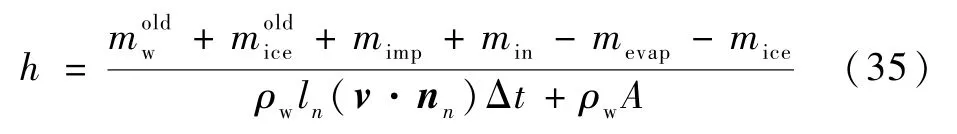
观察式(6)、式(35)可知,水膜流动速度和水膜厚度相互影响,相互耦合,无法单独求解,需要联立求解。通过Jacobi迭代法和Gauss-Seidel迭代法,在对单一控制体迭代计算时,将该控制体上一迭代步骤计算结果中的水膜厚度和水膜速度带入当前迭代步骤,循环迭代求解式(6)得到水膜速度用于判定流入流出水量和方向,再通过式(35)求出当前迭代步骤的水膜厚度,与水膜速度一起用于下一迭代过程,直至水膜流动速度和水膜厚度达到收敛,当前控制体计算完成,可用于结冰计算。
在全部控制体结冰计算完成后,利用更新后的水膜厚度和水膜速度,从步骤1开始重新判定流动速度和流动方向,再次对所有控制体进行结冰计算,直至前后2次计算误差达到一定程度,完成收敛。通过计算单一控制体内收敛和全部控制体收敛,在个体-整体双重收敛的作用下,完成对水膜流动速度和水膜厚度的计算。
通过迭代计算得到水膜厚度和水膜流动速度后,即可得明冰状态下的结冰参数:

③当f=0时,说明此时控制体内不结冰,只存在液态水膜,即mice=0,且由式(35)可知水膜厚度为
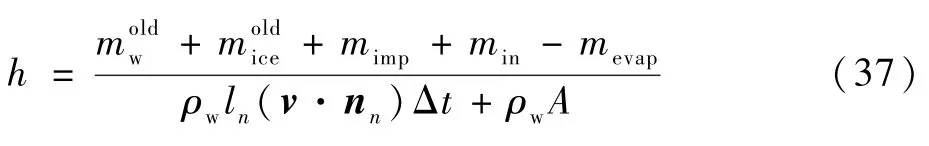
联立式(6)和式(37),采用明冰计算时的迭代求解方法,可得水膜厚度和流动速度,从而得到液态水状态下相应的结冰参数:
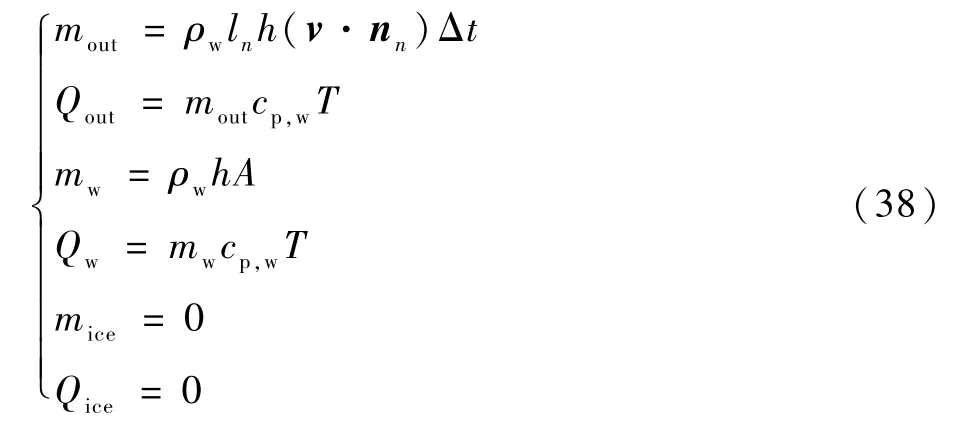
3)通过对f的判断可以得到控制体内的结冰状态,从而计算得到当前时间步长控制体的溢流水流出量,水膜厚度和结冰量,然后将当前控制体溢流水流出量作为输入值,赋值给临近控制体。
4)进行下一控制体计算,直至全部控制体计算完成,并利用更新后的水膜厚度,对控制体内水膜速度进行更新,返回步骤1重新计算,直至完成收敛,则当前时间步长计算完成。
3 仿真计算分析
针对飞机上的所有旋转部件结冰进行研究,分析旋转部件的结冰特性,为便于仿真模型扩展到所有旋转部件,参考文献[17]的处理方式,将简化后的等截面圆柱作为结冰壁面,其直径为60mm,长度为200mm,对称安置于直径600mm的转轴上,来流空气沿转轴轴向方向,如图5所示。
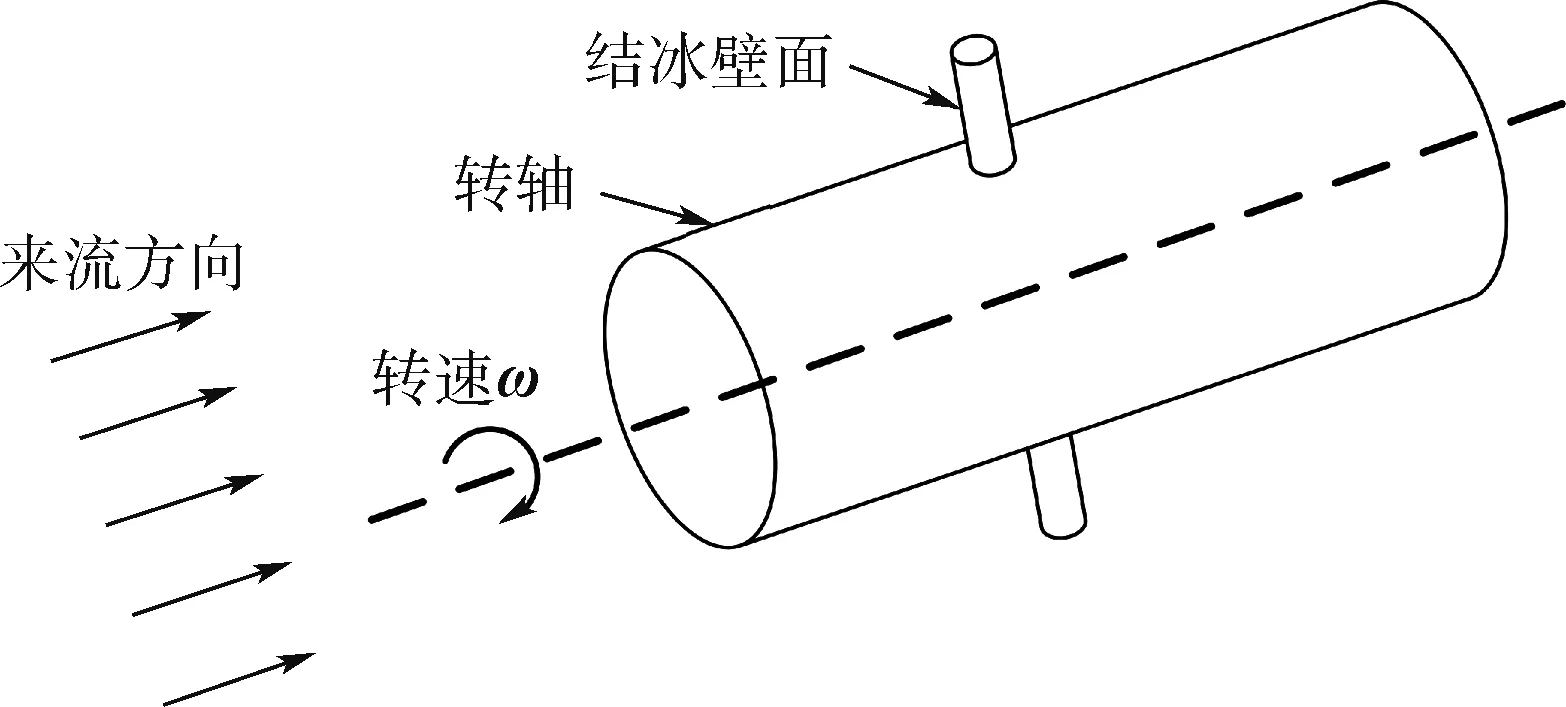
图5 旋转圆柱模型示意图Fig.5 Schematic diagram of rotating cylinder model
将入口来流边界设为速度进口,出口边界设为压力出口,结冰表面和转轴均设为旋转壁面,计算条件为:压力101325Pa,迎角0°,结冰温度263.15K,来流速度60m/s,转速30rad/s,液态水含量(LWC)0.8g/m3,水滴直径20μm,结冰时间420s。取时间步长0.02s与0.05s进行验证计算,对比结果发现最终结冰冰形和水膜相近,本文取时间步长0.05s进行计算,所得圆柱三维结冰冰形如图6所示,圆柱中间截面上的二维冰形和水膜厚度随时间变化如图7和图8所示。
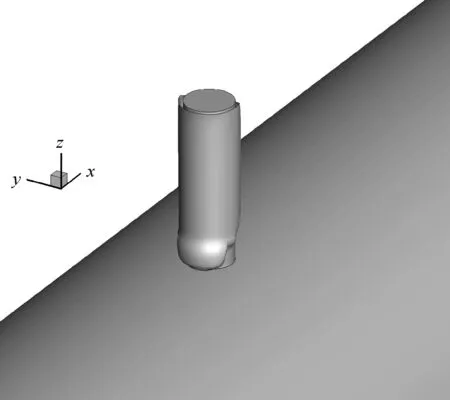
图6 旋转圆柱三维冰形Fig.6 Three-dimensional ice shape of rotating cylinder
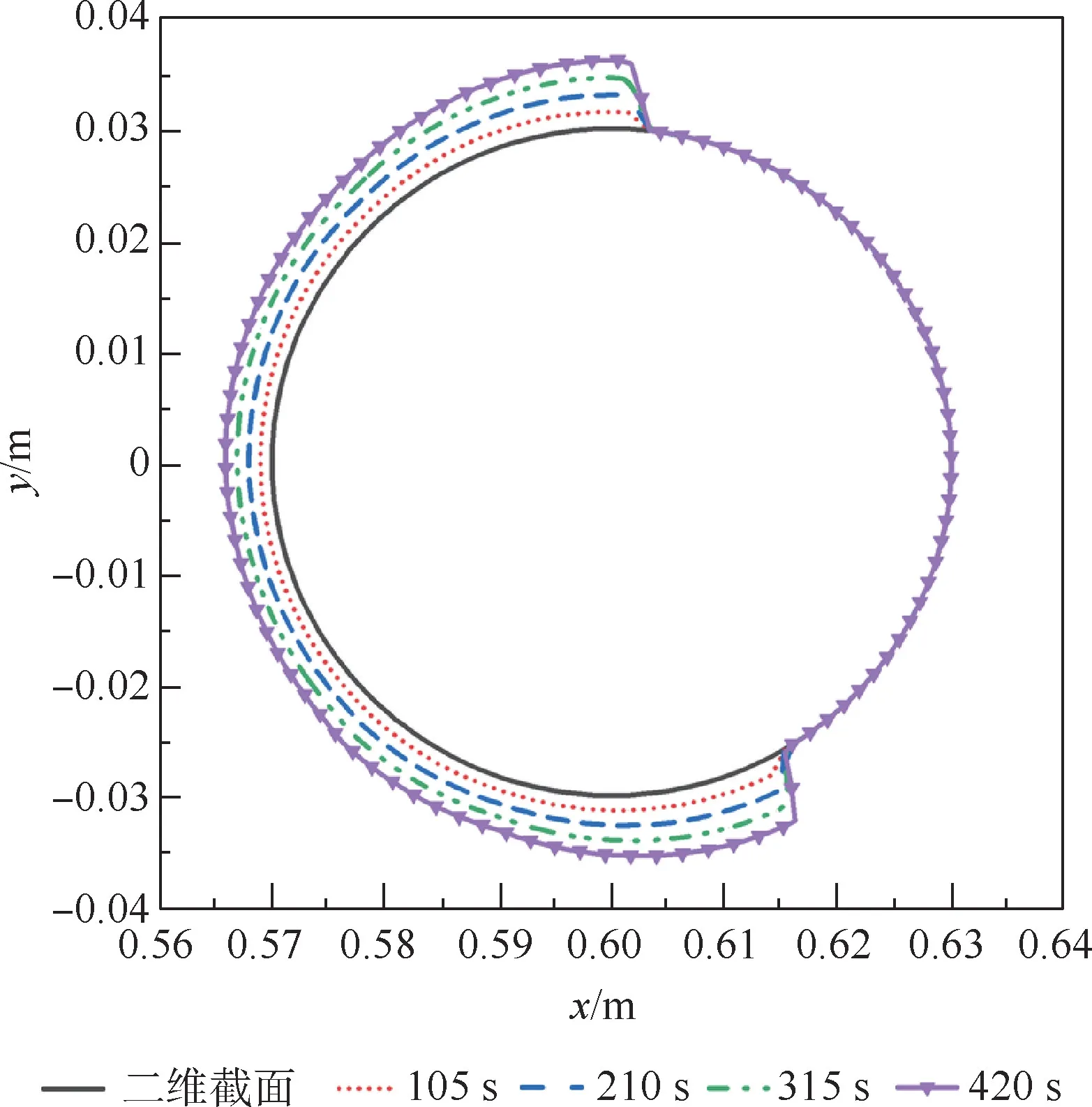
图7 结冰冰形随时间变化Fig.7 Ice shape changing over time
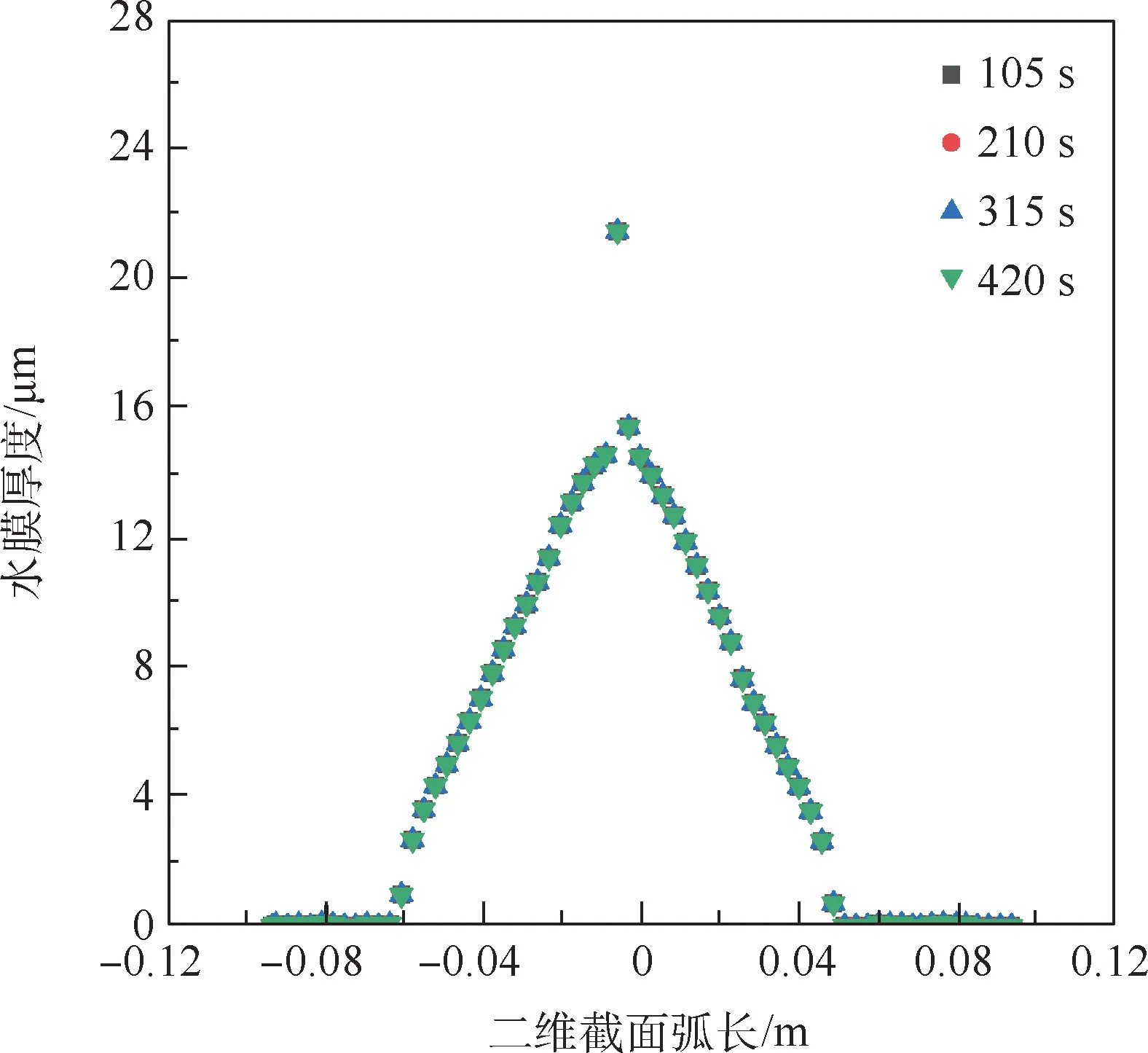
图8 水膜厚度随时间变化Fig.8 Water film thickness changing over time
由图7和图8可知,随着结冰时间的增长,不断有撞击水撞击到结冰壁面上,结冰表面水收集量逐渐增多,导致圆柱表面结冰厚度逐渐增加,当结冰环境温度不变时,结冰能力基本不变,只有厚度随时间发生明显变化;且随着时间的增长,水膜厚度和覆盖范围变化很小,水膜达到一定结冰时间后基本不变。同时由于旋转的作用,圆柱表面上的结冰区域和水膜覆盖区域均向圆柱下表面(-y方向)发生偏移,下表面的结冰区域和水膜覆盖范围大于上表面。
水膜厚度虽然整体变化趋势符合预期,但是在驻点处数值偏大,通过对数据进行分析,推测由于驻点处速度趋近于0,水膜在驻点处基本不发生溢流,液态水在该点产生积聚,导致驻点处水膜厚度偏大。可在之后的研究中加入压力的影响,当剪切力趋于0时,将压差作为驻点处水膜流动的主要驱动力,对模型算法进一步改进。
由于旋转表面结冰实验研究匮乏,缺乏相关实验数据用以验证数值模拟的准确性,因此为了验证所提模型的可靠性,将该模型算法的结冰计算结果与FENSAP软件获得的结冰冰形进行对比,来验证所提模型的合理性。在转速为30rad/s,结冰时间420s的工况下开展计算,将最终冰形结果进行对比,如图9和图10所示。
观察图9和图10的对比可知,两者的结冰厚度和结冰范围基本相同,其中本文所搭建的结冰模型的结冰范围略微偏小;两者的冰形变化趋势也基本一致,在旋转作用下同样向圆柱下表面发生了偏移;水膜厚度变化曲线基本吻合,只有在驻点处由于速度趋近于0,使得结冰模型计算精度不够,水膜厚度数值偏大,其余点处吻合良好。本文模型与FENSAP计算结果对比分析,证明本文模型的结冰冰形和水膜溢流计算结果合理,所提结冰模型求解方法正确。
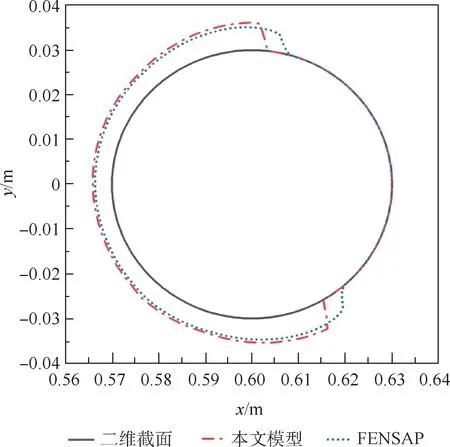
图9 本文模型和FENSAP冰形结果对比Fig.9 Comparison of ice shape between the proposed model and FENSAP
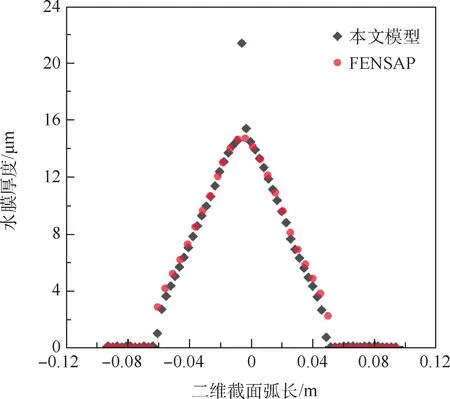
图10 本文模型和FENSAP水膜厚度对比Fig.10 Comparison of water film thickness between the proposed model and FENSAP
通过改变转速,研究转速对旋转圆柱表面结冰和水膜流动的影响,将转速分别设为0,30,60rad/s,其二维中间截面的结冰冰形和水膜厚度如图11和图12所示。
根据图11和图12比较3种不同转速结果可知,随着转速的增加,水膜受到的惯性力和空气剪切力等逐渐增加,圆柱表面液态水的溢流能力逐渐增强,结冰范围和水膜覆盖范围向圆柱下表面(-y方向)出现明显偏移,转速越大,偏移现象愈加明显。且随着转速的增加,冰层厚度基本不变,水膜厚度略有减小。
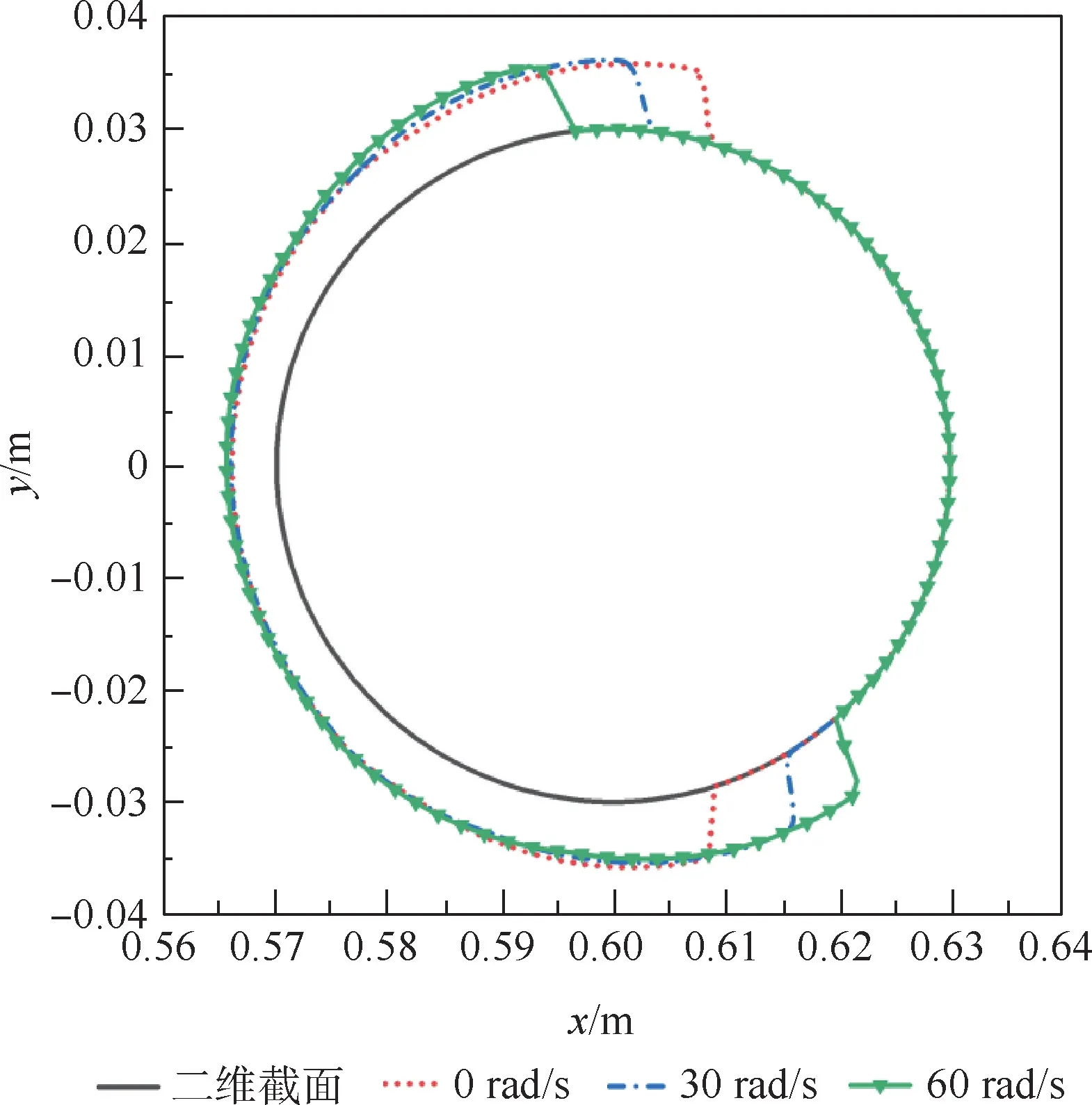
图11 结冰冰形随转速变化Fig.11 Ice shape changing with speed
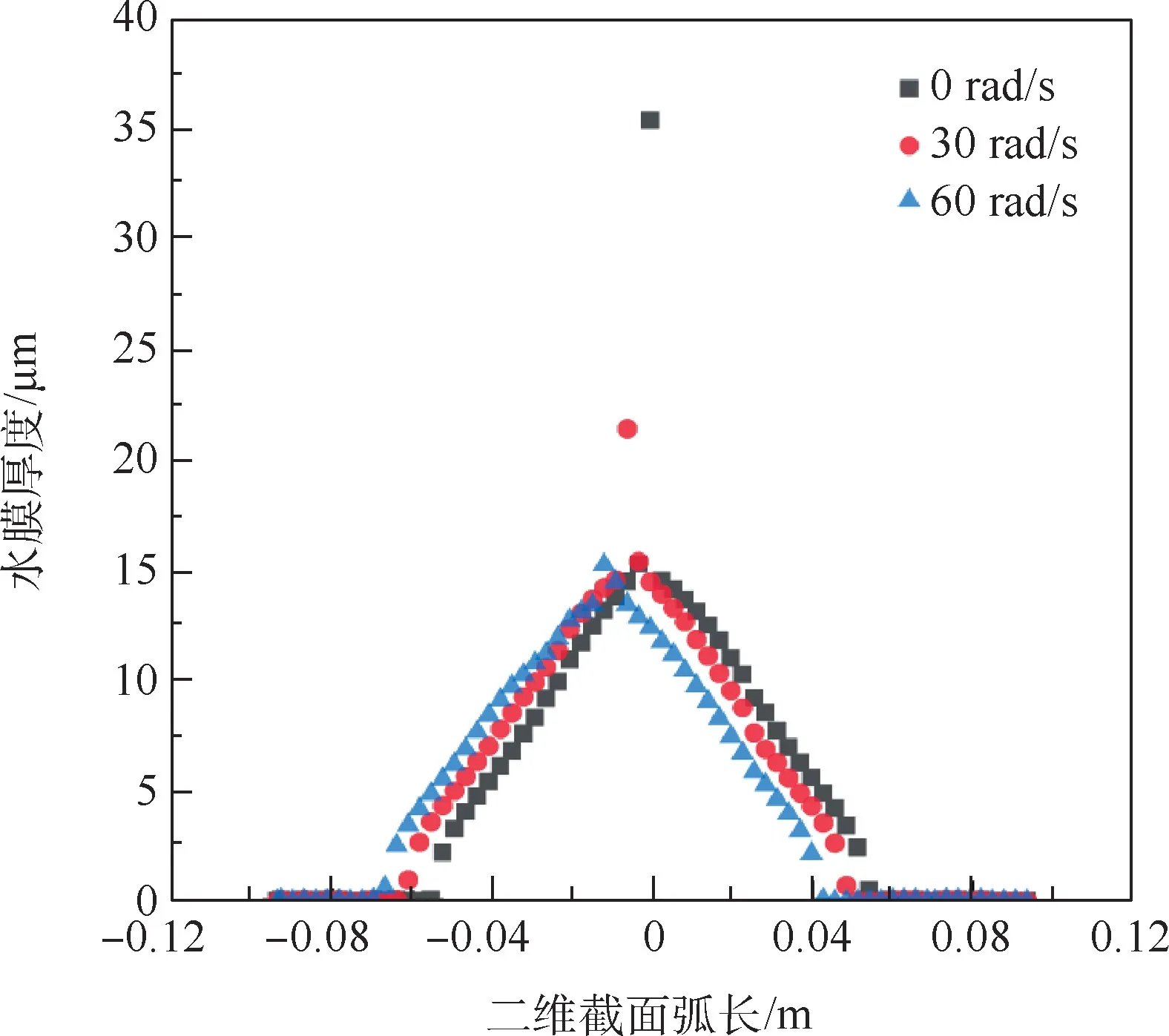
图12 水膜厚度随转速变化Fig.12 Water film thickness changing with speed
通过改变撞击水滴的直径,研究其对旋转圆柱表面结冰和水膜流动的影响,撞击水滴直径分别设为20,25,30μm,其二维中间截面的结冰冰形和水膜厚度如图13和图14所示。
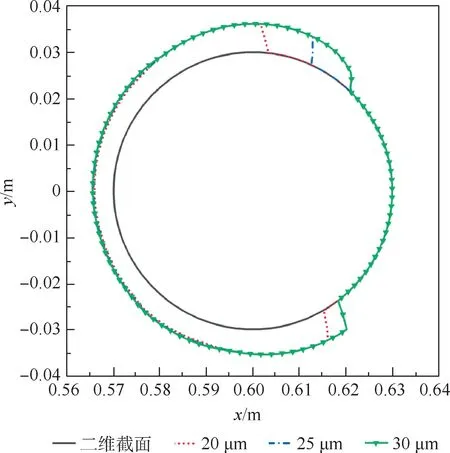
图13 结冰冰形随水滴直径变化Fig.13 Ice shape changing with droplet diameter
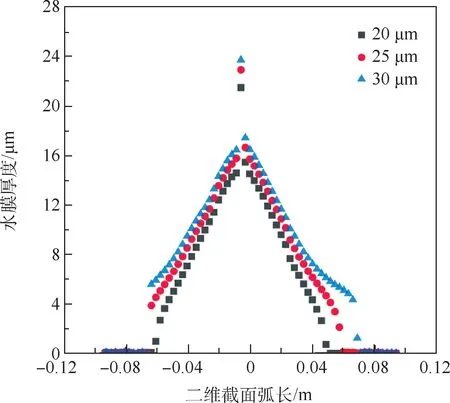
图14 水膜厚度随水滴直径变化Fig.14 Water film thickness changing with droplet diameter
通过图13和图14比较3种不同撞击水滴直径的计算结果可知,随着水滴直径的增加,水滴惯性更大,不易受到气流的作用而绕过迎风表面,更容易和圆柱表面发生碰撞,水滴撞击范围和撞击量相应增加,同时由于当前环境结冰能力恒定,冰层厚度随水滴直径变化较小,未凝结的液态水相应增多,会在空气剪切力和离心力等的作用下发生溢流,因此结冰范围和水膜覆盖范围随水滴直径增长而逐渐增加,水膜厚度也逐渐增大。
通过改变液态水含量,研究其对旋转圆柱表面结冰和水膜流动的影响,液态水含量分别设为0.6,0.8,1.0g/m3,其二维中间截面的结冰冰形和水膜厚度如图15和图16所示。
由图15和图16比较3种不同液态水含量的仿真计算结果可知,随着液态水含量的增长,相同时间撞击到迎风表面的水滴增多,导致圆柱表面的液态水逐渐增多,同时由于当前结冰环境的结冰能力恒定,结冰厚度只发生了小幅度增长,可溢流的未凝结液态水逐渐增多,水膜厚度也相应增加,在空气剪切力和离心力等的作用下,未凝结水膜发生溢流,其覆盖范围明显变大,结冰范围也明显增加。

图15 结冰冰形随液态水含量变化Fig.15 Ice shape changing with liquid water content
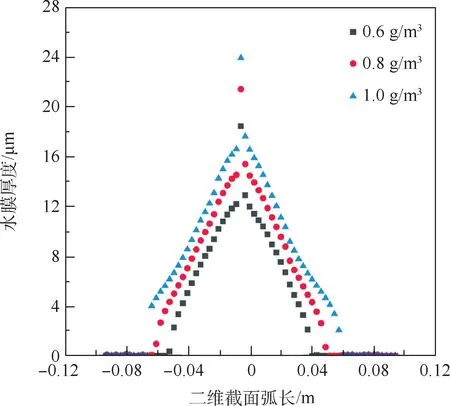
图16 水膜厚度随液态水含量变化Fig.16 Water film thickness changing with liquid water content
4 结 论
考虑旋转部件表面的水膜流动受到空气剪切力与惯性力影响,建立了旋转表面的结冰热力学模型,通过个体-整体双重收敛的方式进行非稳态迭代求解。以旋转圆柱表面为研究对象,分析各影响因素对结冰和水膜流动的作用,得出以下结论。
1)所提模型的非稳态求解方法经过验证,可以有效对三维旋转部件表面的结冰冰形和水膜流动进行模拟,在驻点处水膜计算尚存在不足,可在之后的研究中对模型算法进一步改进。
2)由于旋转的作用,圆柱表面的结冰区域和水膜覆盖范围会发生偏移,且随着结冰时间的增长,旋转圆柱表面的结冰厚度也随之增加,其结冰区域和水膜溢流受结冰时间影响较小。
3)随着转速的增加,旋转圆柱表面结冰区域和水膜覆盖范围的偏移现象愈加明显,冰层厚度基本不变,水膜厚度略微减小。
4)随着水滴直径的增加,旋转圆柱表面的冰层厚度变化较小,其结冰区域和水膜覆盖范围随水滴直径增长逐渐增加,水膜厚度也逐渐增大。
5)随着液态水含量的增长,旋转圆柱表面的结冰厚度出现小幅增长,水膜厚度相应增加,结冰范围和水膜覆盖范围也明显变大。
