尾迹对低压涡轮吸力面附面层流动的影响

曹惠玲，吴兴爽，谭天荣，宋立旗，刘福林

（中国民航大学航空工程学院，天津 300300）

0 引言

低压涡轮（Low Pressure Turbine，LPT）的级数和叶片较多，是影响航空发动机效率和质量的重要部件之一。采用高负荷LPT叶片设计可有效地减少叶片数量，研究并理解LPT内部流动特性及其机理有助于LPT设计。Curits等[1]发现吸力面产生的气动损失占叶型损失的60%；Mayle[2]发现LPT在低雷诺数下工作时，其吸力面附面层可能会发生分离，造成严重的气动损失使发动机效率降低。此外，在LPT工作时，上游叶片产生周期性非定常尾迹将影响下游叶片的附面层流动。

一方面，大量学者针对低雷诺数下的低压涡轮非定常流动进行了研究。Kaszeta等[3]研究了尾迹对低压涡轮叶栅转捩和分离的影响，指出尾迹产生的湍流使湍流水平总体上升；Zhang等[4]结合雷诺数和湍流度研究了非定常尾迹对超高负荷低压涡轮附面层的影响，并指出在低湍流低雷诺数下，尾迹与分离附面层的相互作用主要是由尾迹负射流诱导的卷起涡引起的；Wolff等[5]使用热线研究了超高负荷低压涡轮叶片的非定常尾迹诱导附面层发展特性，并指出非定常尾迹在低雷诺数下对分离泡的抑制有助于减小叶型损失。

另一方面，学术界对于附面层内部流动特性与转捩机理的研究也较为深入。Jacobs等[6]发现Klebanoff条纹因叶片前缘的“剪切遮蔽”效应产生；Liu等[7]发现自由流湍流会在附面层内诱导出弱Klebanoff条纹；Coull[8]发现尾迹放大Klebanoff条纹的前缘、最强条纹、尾缘分别以88%、70%、50%的主流速度向下游运动；Wissink等[9]在尾迹扫掠分离剪切层时，观测到因开尔文-亥姆霍兹（Kelvin-Helmholtz，KH）不稳定性诱导形成了全展向卷起涡结构；McAuliffe等[10]发现Klebanoff条纹会扭曲分离剪切层，并抑制全展向KH卷起涡结构的形成。

中国针对非定常尾迹影响叶片流动特性问题开展了大量研究。王英峰等[11]采用频谱分析的方法进行了上游尾迹对叶片分离的影响研究；罗华玲等[12]研究了尾迹在叶栅中的输运及叶片排之间的时序效应；李虹杨等[13]应用自行开发的CFD程序对周期性尾迹作用下的涡轮叶栅附面层转捩进行了研究；Sun等[14-15]研究了上游尾迹对低压涡轮叶片附面层发展的影响，并对比了采用三角棒和圆棒模拟上游尾迹对吸力面附面层流动与转捩的影响。但中国学者对附面层瞬态分析的研究却较为有限。Cui等[16-17]、Sun等[18]、Nagabhushana等[19-20]虽对叶栅通道内的瞬态结构进行了分析，但主要集中于LES模型在主流与端区中的应用，对于尾迹诱导转捩和自然转捩相互转换主导附面层转捩这一过程并无完整的时空演化分析。

本文在1个完整尾迹扫掠周期内对尾迹在叶片前缘形成的瞬态结构进行了研究，并分析了瞬态结构对吸力面附面层流动特性与多模态转捩的影响。

1 试验与数值模拟

1.1 试验设置

试验研究依托低速叶栅试验台进行，带上游圆棒的叶栅通道模型及叶栅测试试验台照片如图1所示，叶栅和圆棒参数及来流条件见表1。叶栅试验台使用运动圆棒模拟从上游叶片尾缘脱落的尾迹。圆棒安装在由交流电机驱动的辐条尾迹发生器上，并使用光电转速传感器测量辐条转速。从图1（a）中可见，气流出口平面到叶片尾缘的距离为Cx，圆棒到叶片前缘的距离为0.6Cx，圆棒进口平面到圆棒的距离为0.6Cx，栅距方向上的两边界间的距离为1个栅距P，圆棒间距为P。使用DSA 3217压力传感器测量吸力面壁面静压，表面压力信号使用DSA 3217压力传感器进行测量。DSA 3217压力传感器包含16个温度补偿压阻式压力传感器和1个气动校准阀、内存、16位A/D转换器，以及1个微型处理器。微型处理器用于补偿温度变化，控制校准阀已执行在线零位和多点校准，并能够消除传感器热误差，保证系统精度为0.05%。使用5孔探针和热线分别测量出口动压与近壁面速度。

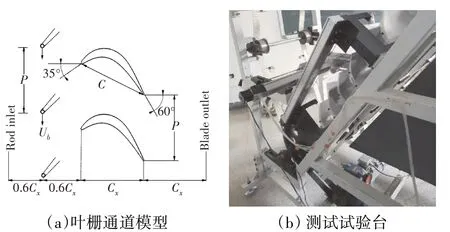
图1 带上游圆棒的叶栅通道模型及叶栅测试试验台

表1 叶栅和圆棒参数及来流条件

本文选取较低的雷诺数Re=50000和较低的自由来流湍流度Fsti=1.5%作为来流条件，根据真实LPT工况选择流量系数Ф=1，折合频率Fr=1.128。

流量系数定义为

式中：Ux为轴向速度；Ub为尾迹发生器移动速度。

折合频率定义为

式中：Cx为轴向弦长；P为栅距。

1.2 数值模拟

本文使用商用CFD软件对流动进行仿真，采用LES湍流模型耦合Smagorinsky亚格子模型进行数值模拟，并通过试验校核。空间离散项设置为中心差分，时间离散项设置为2阶精度向后欧拉积分。同时为弥补Smagorinsky亚格子模型带来的近壁面涡黏度过大的问题，采用Van-Driest壁面函数[21]进行修正，并将Smagorinsky系数设为0.1。Funazaki[22]指出，对于高质量、网格点数多的计算网格，基于LES模型耦合Smagorinsky亚格子模型的数值仿真能够准确地模拟吸力面附面层特性。

Packb网格拓扑和计算域如图2所示。Wu等[23]的研究表明计算域展向宽度不应影响展向或流向的涡结构发展。为保证能够捕捉详细的瞬态结构进行分析，本文仿真的计算域展向宽度定为0.18Cx。环绕叶片近壁面区域1周为“O”型拓扑，其外围区域为“H”型拓扑。计算域网格在x方向上有560个节点，y方向上有225个节点，z方向上有51个节点，x-y平面上环绕叶片近壁面1周的网格节点数为770。同时叶片壁面法向上第1层网格最大高度设置为0.003 mm，约为栅距的4.5×10-5倍，以保证在该雷诺数下y+＜1。为捕捉附面层的发展，在叶片壁面法向上12%的栅距长度内，设置了100个节点，并保证x+、y+小于40。在叶片计算域内约有700万个节点，在尾迹发生器计算域内则有约80万个节点，整个计算域约有800万节点。

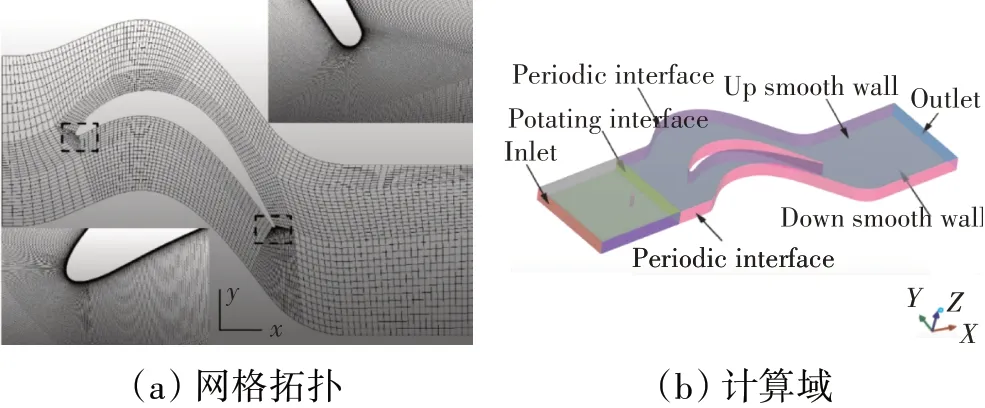
图2 Packb网格拓扑和计算域

时间步长约为Δt=0.0256 ms，Courant数（UinΔt/Δxmin）约为0.176（Uin为进口速度，Δxmin为网格在x方向的最小长度）。每个尾迹扫掠周期T=2000Δt。为保证数值模拟的稳定性，采用收敛的雷诺平均（Reynolds Average Navier Stokes，RANS）结果作为初场，再采用SST-SAS模型计算1个尾迹扫掠周期，最后采用LES模型耦合Smagorinsky亚格子模型计算10个尾迹扫掠周期。统计时均结果时，排除第1周期，对剩余的9个周期每隔3个周期进行锁相平均。使用1台10核20线程的工作站进行计算，每个工况耗时25天。

1.3 试验验证

本文吸力面时均静压系数Cp的定义为

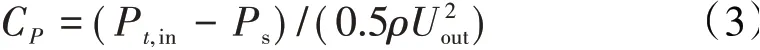
式中：Pt,in为进口总压；Ps为当地静压；ρ为密度；Uout

吸力面时均静压系数试验结果与数值模拟结果对比如图3所示，其中吸力面流向位置s通过吸力面弧长S0进行无量纲化。

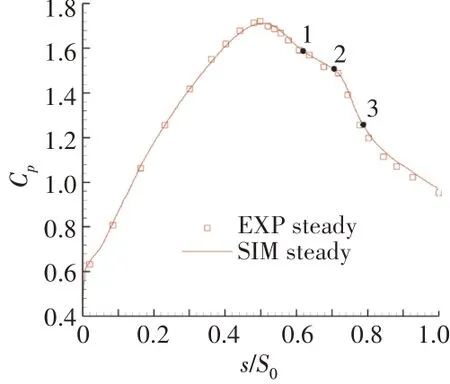
图3 吸力面时均静压系数试验结果与数值模拟结果对比

从图中可见，数值模拟结果与试验结果在速度峰值点、“平台”起始点、“平台”结束点和压力恢复点等位置基本吻合。同时用黑点和数字分别将数值模拟结果的时均分离起始点、时均转捩点和时均再附点标出。一般认为，在形状因子H12＞3.5时附面层发生分离[24]，在间歇因子＞0.25时开始发生转捩。通过计算各时刻的形状因子和间歇因子并进行时均处理，得到时均分离起始点1位于60%S0，时均转捩点2位于70%S0，时均再附点3位于78%S0。其中间歇因子采用Solomon等[25]给出的方法计算。

Mayle[2]认为LPT中的转捩类型主要有旁路转捩和分离流转捩，分离流转捩可能观察不到T-S波的存在，但KH不稳定性在这2种转捩类型中均起到了重要的作用。T-S波通常出现在转捩过程的初期，是最先出现在层流流动中的不稳定性表现形式，Walker[26]建立了T-S波频率fTS和附面层参数间的经验公式，并将fTS定义为

式中：Ue为附面层边缘速度；δ*为T-S波第1次出现在层流附面层内时对应位置的位移厚度；ν为动力黏度。

经计算，在Re=50000工况下，fTS≈220 Hz。根据Hughes等[27]的研究结果，式（4）计算的fTS为最大的放大率，在试验中还能观测到更低的T-S波频率。Graveline等[28]计算的T-S波频率与试验观测也存在一定误差，但仍处于同一量级。

Volino[29]建立了KH不稳定性主导频率的经验公式，并将其定义为

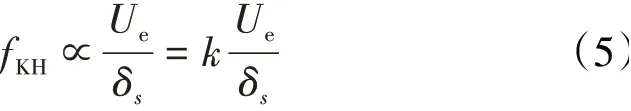
式中：δs为自由剪切层厚度；k为系数，Volino[29]认为k≈1.0。

经计算，本文fKH≈2800 Hz。Graveline等[28]认为频谱图中的峰值与涡扫过热线探头有关，当涡结构通过热线时会在频谱图上留下1个频率范围较宽的峰值，并认为该峰值是由KH不稳定性造成的。Tennekes等[30]指出涡的频率约为0.6f~1.6f，其中f与涡通过的频率有关。因此表征KH不稳定性的fKH不仅随流向位置的变化而变化，反映到频谱图中还应当是1个范围值。

此外，已有不少研究在理想试验条件[31-32]和CFD结果[33]中观测到KH涡在向下游运动的过程中会发生涡配对（vortices pair-up）现象，意味着在涡向下游运动的同时fKH会减半。

本文还使用热线对吸力面表面的速度进行测量，并对无量纲流向速度扰动量的平方进行频谱分析得到能谱函数E1(f)，其中为流向扰动速度，Umain为主流速度，f为频率。吸力面壁面速度频谱试验结果与数值模拟结果对比如图4所示。对吸力面壁面50%S0（层流）、70%S0（转捩过程中）、80%S0（完全湍流）位置处的频谱进行对比，并用黑色圆圈圈出尾迹扫掠扰动（wake passing）、fTS和fKH。

图4 吸力面壁面速度频谱试验结果与数值模拟结果对比

从图4（a）中可见，约在125 Hz时出现的第1个明显的波峰是由尾迹扫掠造成的，其对应的频率与尾迹扫掠的频率基本符合；在170~190 Hz时出现了第2个明显的波峰，这与本文计算的fTS≈220 Hz处于同一量级，因此可以认为第2个波峰是由T-S波造成的。在2400~3600 Hz内可观测到较为明显的宽峰，根据Graveline等[28]和Tennekes等[30]的研究可知该宽峰是由KH不稳定性引起的，同时在80%S0频谱图1000~1500 Hz内可观测到另1个宽峰，这是由KH涡向下游运动时发生的涡配对现象引起的频率减半。此外，在80%S0时处于完全湍流状态的频谱线在103＜f＜104内的衰减规律符合-5/3原则。

对比图4（a）、（b）可知，试验和数值模拟得到的尾迹扫掠、fTS、fKH的频率基本吻合，在80%S0时频谱在103＜f＜104内衰减规律均符合-5/3原则，因此认为数值仿真能够准确地模拟吸力面附面层流动特性。

2 结果分析

主要对上游尾迹与吸力面附面层相互作用以及多种类型转捩的瞬态流动特性进行了分析。在1个尾迹扫掠周期内叶栅通道的瞬态流动细节如图5所示。图中叶栅通道截面使用湍动能（Turbulence Kinetic Energy，TKE）云图标注尾迹与附面层展向卷起涡，并用红线标出了近壁面速度流线。为观测尾迹与附面层的作用以及附面层内部的瞬态流动结构，使用距离叶片吸力面的半附面层高度作为观测面，在20张瞬态流动图中给出了观测面上的湍动能TKE、无量纲壁面法向涡量wy*和无量纲壁面法向速度uy*。根据Coull[8]的研究可知，一定强度的wy*和uy

*能够反映出附面层内Klebanoff条纹和KH结构。其中wy*越大，速度亏损越大，Klebanoff条纹的强度也越强。根据Jeong等[34]的研究可知，可以使用速度梯度张量特征方程的第2个不变量Q来标识涡结构，Q=0.5(||Ω2||-||S2||)，其中S为剪切应变率，Ω为涡量。当Q＞0时，存在涡结构。因此在图5（a）左下角使用Q等值面（Q=1.5×107）标出了65%S0~100%S0的近壁面涡结构和半附面层高度观测面的wy*云图。在图5中还使用红色实线和字母标记出了尾迹前缘线L、尾迹中心线A、尾迹尾缘线T、尾迹诱导转捩区尾缘线B和抑制区尾缘线C的位置。这些位置线通过计算各流向位置附面层边缘速度扰动在时间上的分布，并根据速度扰动波峰波谷来确定。尾迹与附面层作用将诱导附面层发生转捩形成湍斑，在向下游运动和生长的过程中，湍斑后部会形成1个抑制区，湍斑尾缘和抑制区尾缘分别以50%和33%的主流速度向下游运动。一般认为当间歇因子大于0.25时，转捩开始发生。本文采用Solomon等[25]给出的方法计算间歇因子。

图5 在1个尾迹扫掠周期内叶栅通道的瞬态流动

从图5（a）中可见，在0.05T时，上一条尾迹已经离开叶栅通道，其诱导产生的转捩区尾缘线B和抑制区尾缘线C尚未离开观测面，表明上一条尾迹产生的尾迹诱导湍流区和抑制区在叶片尾缘与附面层发生相互作用；在70%S0~75%S0附近有强度较弱的流向结构（黑色椭圆圈出），从左下角的涡结构示意图中可见相似的流向结构（黑色椭圆圈出），二者可以对应，表明上一条尾迹产生的尾迹放大Klebanoff条纹仍与叶片尾缘附近的附面层发生相互作用；同时，在该时刻下一条尾迹W1尚未与吸力面接触，处于尾迹通过的间歇期，因此无法在叶片前部观测到明显的流向条纹结构；在C线上游、L线下游的65%S0~75%S0区域内有涡卷起现象（箭头标出），以及涡卷起造成的观测面的湍动能增大。此时处于尾迹扫掠的间歇期，同时上一条尾迹产生的抑制区尾缘线C正在离开时均分离区域，表明吸力面附面层转捩模式正在由尾迹诱导转捩向自然转捩转变。

从图5（b）中可见，在0.10T时，尾迹W1尚未与吸力面接触，依然无法在叶片中部观测到明显的Klebanoff条纹，从流线和左下角的涡结构示意图中可见涡卷起并向下游运动，造成观测面上湍动能TKE增大。此时处于尾迹扫掠的间歇期，同时抑制区尾缘线C已离开时均分离区域，吸力面附面层的转捩模式为自然转捩。

从图5（c）、（d）中可见，在0.15T~0.20T时，随着尾迹向下游运动，在尾迹中心线A附近观测到流向条纹结构（黑色椭圆圈出），这是由于尾迹扰动在渗透入吸力面前缘的附面层时，因“剪切遮蔽”效应形成尾迹放大Klebanoff条纹，尾迹放大条纹区前缘和尾缘分别以88%和50%的主流速度向下游运动，其中最强条纹以70%的主流速度向下游运动，因此条纹将始终落后于尾迹前缘线L。

从图5（e）中可见，在0.25T时，尾迹W1开始与吸力面附面层接触并发生相互作用，尾迹前缘线L抵达70%S0，并进入分离剪切层中，尾迹扰动开始渗透进入分离剪切层并触发KH不稳定性，展向的KH涡不断地沿分离泡边缘形成、脱落并向下游运动；从近壁面流线和左下角的涡结构示意图中可见65%S0~70%S0区域内有全展向KH结构（Full Span K-H Structure）（箭头标出，标记为1），该KH结构以37%的主流速度向下游运动并抬起，此时无法在观测面uy*云图上观测到展向结构，这是由于该展向结构尚未抵达半附面层高度。

从图5（f）中可见，在0.30T时，标记为1的全展向KH结构在向下游运动的同时不断抬起，并抵达半附面层高度，因此在观测面uy*云图72%S0附近可观测到类似的展向结构（黑色椭圆标出）。

从图5（g）中可见，在0.35T时，左下角涡结构示意图标记为2的全展向KH涡紧随全展向KH涡1于71%S0附近形成，并向下游运动，在uy*云图的对应位置可见完整的全展向KH结构；同时，从观测面的wy*云图中可见，尾迹放大Klebanoff条纹的发展呈现出楔形的展向不对称性，这一楔形分布与观测面的湍动能分布形态吻合，与Nagabhushana[19]所观测到的条纹展向不对称性相似；从观测面的wy*云图中还可见，尾迹放大Klebanoff条纹最前缘抵达65%S0，尚未与位于71%S0的KH结构接触，因此可以观测到较为完整的全展向KH结构1、2。

从图5（h）中可见，在0.40T时，尾迹放大Klebanoff条纹与全展向KH结构接触，同时从观测面的uy*云图和涡结构示意图中可见全展向KH结构1、2开始发生扭曲，表明KH结构在尾迹放大Klebanoff条纹的作用下开始崩溃。

从图5（i）中可见，在0.45T时，楔形分布的尾迹放大Klebanoff条纹与全展向KH结构1、2接触，Klebanoff条纹会先冲击全展向KH结构的一侧，并使全展向KH结构的一侧发生剧烈扭曲（圆圈标出）。

从图5（j）、（k）中可见，在0.50T~0.55T时，已观测不到全展向KH结构，但能在观测面uy*云图的73%S0~82%S0区域内观测到局部KH结构（Part Span K-H Structure）（黑色方框标出），这是由于尾迹放大Klebanoff条纹冲击全展向KH结构，使全展向KH结构破碎为局部KH结构，这一现象可在观测面的wy*云图和uy*云图中观测到；此外，从近壁面流线和涡结构示意图中已观测不到新的卷起涡生成，表明在尾迹的作用下分离泡被完全抑制。

从图5（l）中可见，在0.60T时，随着尾迹放大，Klebanoff条纹不断向下游运动并破坏KH结构，从涡结构示意图和uy*云图中已看不到明显的局部KH结构；同时，从wy*云图中可见尾迹放大Klebanoff条纹强度的衰减，这是由于尾迹不断向下游运动，最终不再与叶片前缘发生作用造成的，而已有条纹继续向下游运动、拉伸，强度不断衰减。

从图5（m）中可见，在0.65T时，受尾迹放大Klebanoff条纹影响，已无法观测到明显的KH结构；同时，尾迹诱导吸力面附面层发生尾迹诱导转捩，在T线与B线之间形成尾迹诱导湍流区，在B线和C线之间则形成抑制区，湍流区和抑制区能够有效地抑制分离，因此无法通过近壁面流线观测到涡卷起现象。

从图5（n）中可见，在0.70T时，随着尾迹进一步向下游运动，尾迹尾缘线T抵达78%S0，通过近壁面流线观测到1个较小的涡在70%S0附近卷起，分离泡开始重新生成，因此出现较弱的由于分离的形成而造成的涡卷起现象；此外，在涡结构示意图中的C线下游约75%S0处观测到了Λ涡3的形成，并用箭头标出了Λ涡的2条“腿”，根据Durbin等[35]的研究可知，Λ涡是T-S波和Klebanoff条纹共同作用的结果，由于抑制区内的T-S波扰动较小，因此无法在B线和C线之间的抑制区内观测到明显的Λ涡结构。

从图5（n）、（o）左下角的涡结构示意图中可见，在0.70T~0.75T时，Λ涡3拉伸并最终破裂为湍流。

从图5（p）中可见，在0.80T时，新的Λ涡4在75%S0附近生成；由于尾迹放大Klebanoff条纹在叶片中后部强度衰减，涡的强度变弱，其2条“腿”的不对称性更为明显；同时，随着尾迹向下游运动，抑制区前缘线B不断往下游运动，Λ涡的强度将会变得更弱甚至被抑制。

从图5（q）、（r）中可见，在0.85T~0.90T时，尾迹放大Klebanoff条纹继续向下游运动，其强度不断衰减；Λ涡4在向下游运动的过程中强度不断减弱，2条“腿”的不对称性更为明显；同时，抑制区前缘线B和抑制区尾缘线C分别以50%和33%的主流速度向下游运动，随着时间的推移，抑制区在向下游运动的同时，其所占面积也会增大，一方面抑制区会抑制涡，已无法在涡结构示意图中观测到新Λ涡的生成，另一方面分离泡会在抑制区后重新生成，并能通过抑制区尾缘线C上游的近壁面流线观测到涡卷起现象不断增强，分离泡尺寸也在不断变大；此时尾迹W1即将离开叶栅通道，附面层转捩模式由尾迹诱导转捩向自然转捩过渡。

从图5（r）、（s）、（t）中可见，在0.90T~1.00T时，随着尾迹向下游运动并最终离开叶栅通道，尾迹放大Klebanoff条纹在向下游运动的过程中，其在叶片中后部的强度不断衰减；受抑制区影响，Λ涡在向下游运动的过程中强度也不断减弱；同时，下一条尾迹尚未与吸力面附面层接触，既不会在叶片前部形成尾迹放大Klebanoff条纹，也不会触发分离剪切层的全展向KH卷起涡，无法从wy*云图中观测到明显的流向结构，但能通过流线观测到分离泡以及不断增强的涡卷起现象，并导致观测面TKE增大。

3 结论

（1）在2条尾迹扫掠之间，上一条尾迹刚刚离开叶片尾缘，其尾迹诱导的湍流区和抑制区仍在影响叶片尾缘附面层的发展，同时下一条尾迹尚未与吸力面接触，此时附面层转捩模式由尾迹诱导转捩向自然转捩转变，分离泡在抑制区上游重新生成。

（2）下一条尾迹在叶片前缘与吸力面接触，产生尾迹放大Klebanoff条纹，其前缘以88%的主流速度向下游运动，随后尾迹接触附面层并与分离泡相互作用，触发剪切层的KH不稳定性形成全展向KH卷起涡，并抑制分离泡。尾迹放大Klebanoff条纹将追赶并冲击全展向KH卷起涡，使其崩溃为局部KH涡并最终破裂形成Λ涡和全湍流。